BAI TOAN BIÊN LUÂN NGHIÊM PH NG TRINH ƯƠ
VÔ TI V I NHIÊU CACH GIAI. Ơ
Hâu hêt cac bai toan biên luân nghiêm ph ng trinh đêu co thê giai đ c băng ph ng phap đao ươ ươ ươ
ham( ph ng phap tâp gia tri cua ham), va nêu co thê ta đ a vê xet s t ng giao cua 2 đ ng cong( hinh ươ ư ư ươ ươ
hoc giai tich), hoăc ph ng phap l ng giac. ươ ươ
Vi du1
Cho ph ng trinh ươ
1 8 (1 )(8 ) (*)x x x x m+ + − + + − =
. Đinh cac gia tri m đê ph ng trinh co 2 ươ
nghiêm phân biêt.
Giai.
Cach1 Đăt u= , v= , u≥ 0 , v≥ 0. Ta co hê
2 2
, 0 (1)
9(2)
(3)
1
u v
u v
m u
vu
ì
ï
ï
ï³
ï
ï
ï
ï+ =
í
ï
ï-
ï
ï=
ï
ï+
ï
î
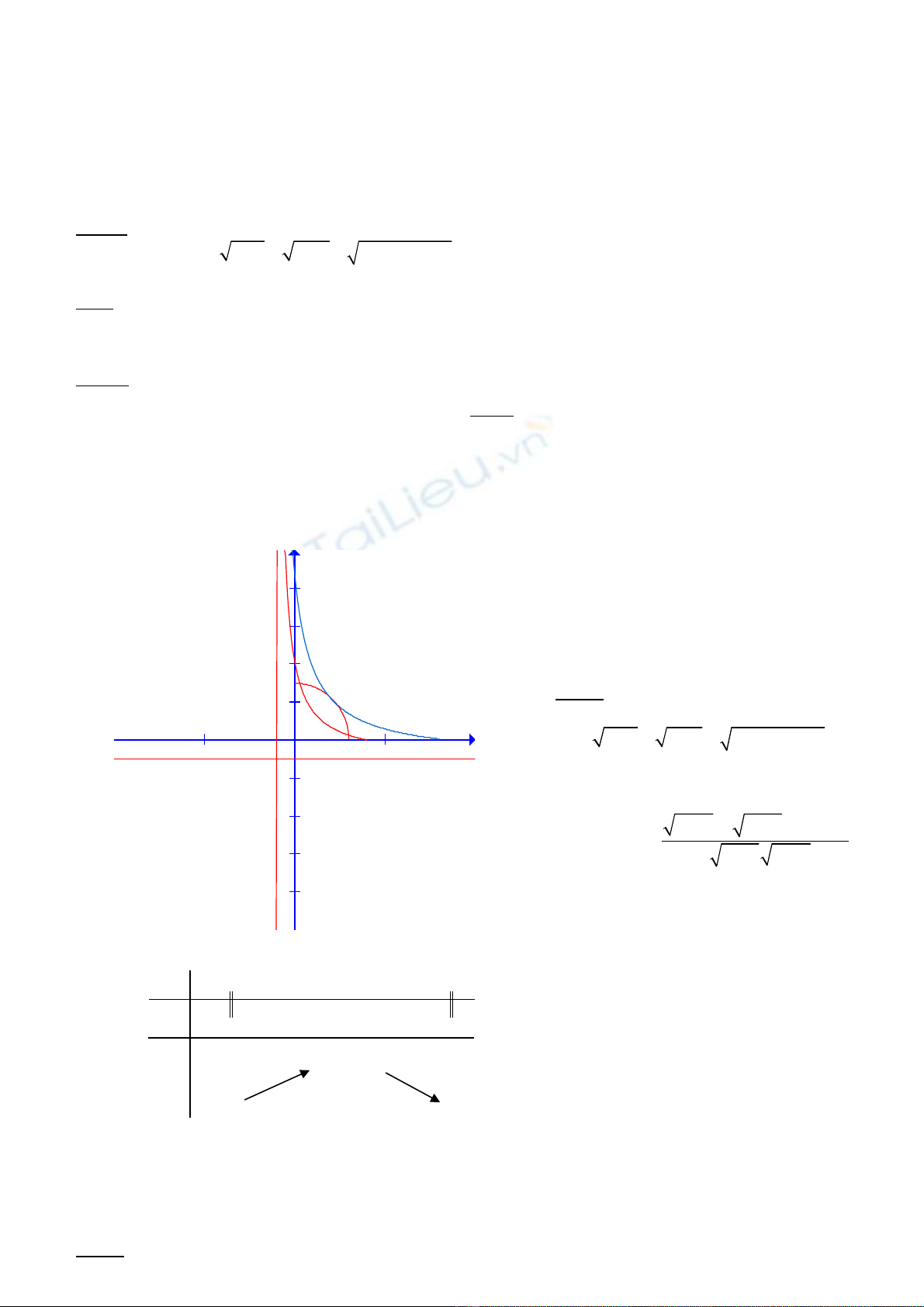
. Xet hê truc Ouv, ve đ ng tron (2) va đô ươ
thi ham (3) la môt hypebol. (*) co 2 nghiêm phân biêt khi (2) va (3) co 2 giao điêm phân biêt.
Nhân xet: m ≤ 0 ph ng trinh vô nghiêm.ươ
Khi m>0 (3) căt Ou, Ov tai hoanh đô m,
tung đô m.
Co môt gia tri m o cho đô thi (3) tiêp xuc
đ ng tron (2) tai I, ta tim toa đô I va mươ o
I la giao điêm cua đ ng thăng y=x va đ ươ ư
ng tron (2). Vây: uơ I= vI= 3/ , thê vao
(3) tim đ c m ươ o= + .
Vây đê thoa điêu kiên đê thi 3 ≤ m≤ +
Cach2 Dung ph ng phap khao sat ham ươ
sô. Xet ham
1 8 (1 )(8 )y x x x x= + + − + + −
Tâp xac đinh D=
1;8
é ù
-
ë û
Đao ham y’=
8 1 2 7
2 1 8
x x x
x x
- - + - -
+ -
y’=0⇔ - =2x-7. Binh ph ng 2 vê cho ph ng trinh hê qua = -2x+14x-20 ươ ươ cuôi cung tim đ c ươ
x= (thoa ph ng trinh xuât phat). ươ
Lâp bang biên thiên:
x -1 8
y’ 0
y +
3 3
Vây đê ph ng trinh co 2 nghiêm phân biêt thi đô thi ham y trên đây căt đ ng thăng y=m tai 2 điêm ươ ươ
phân biêt, vây 3 ≤ m≤ + .3≤ m≤ + .
Cach3 Ph ng phap l ng giac.ươ ươ
-5 5
-8
-6
-4
-2
2
4
6
8
u
v
(3)
(2)
Điêu kiên: -1 ≤ x≤ 8 ⇔ - ≤ x- ≤ . Đăt x- = cos2α v i 0 ơ ≤ 2α ≤ π t c la 0 ư ≤ α ≤ . suy ra x+1=
+ cos2α va 8-x= - cos2α. Vây ph ng trinh (*): cos ươ α + sinα + 3cosαsinα = .
Đăt u= cosα + sinα = sin(α+ ) , vi ≤ α+ ≤ nên 1≤ u≤ , va đ c ph ng trinh: ươ ươ
3u +2u-3= . Lâp bang: α 0
α+
u
1 1
y= 3u +2u-3 3+2
2 2
Theo bang trên: đê yhoar điêu kiên đê thi: 2 ≤ < 3+2 .
Điêu kiên nay ta tim đ c ươ α1 ≠ α2 va d ng thuôc ươ
0; 2
p
é ù
ê ú
ê ú
ë û
. S dung công th c cos2ư ư α = 2 cos α - 1. Dân
đên cos2α1 ≠ cos2α2. T c la xư 1≠ x2; ph ng trinh co 2 nghiêm phân biêt. ươ
Vi du 2 Đinh cac gia tri cua m đê ph ng trinh sau đây co 2 nghiêm phân biêt: ươ
x+ = m
Giai
Cach1 Ph ng phap giao 2 đ ng cong.ươ ươ
Đăt u=x , v= ; v≥ 0. Ph ng trinh t ng đ ng v i hê sau: ươ ươ ươ ơ
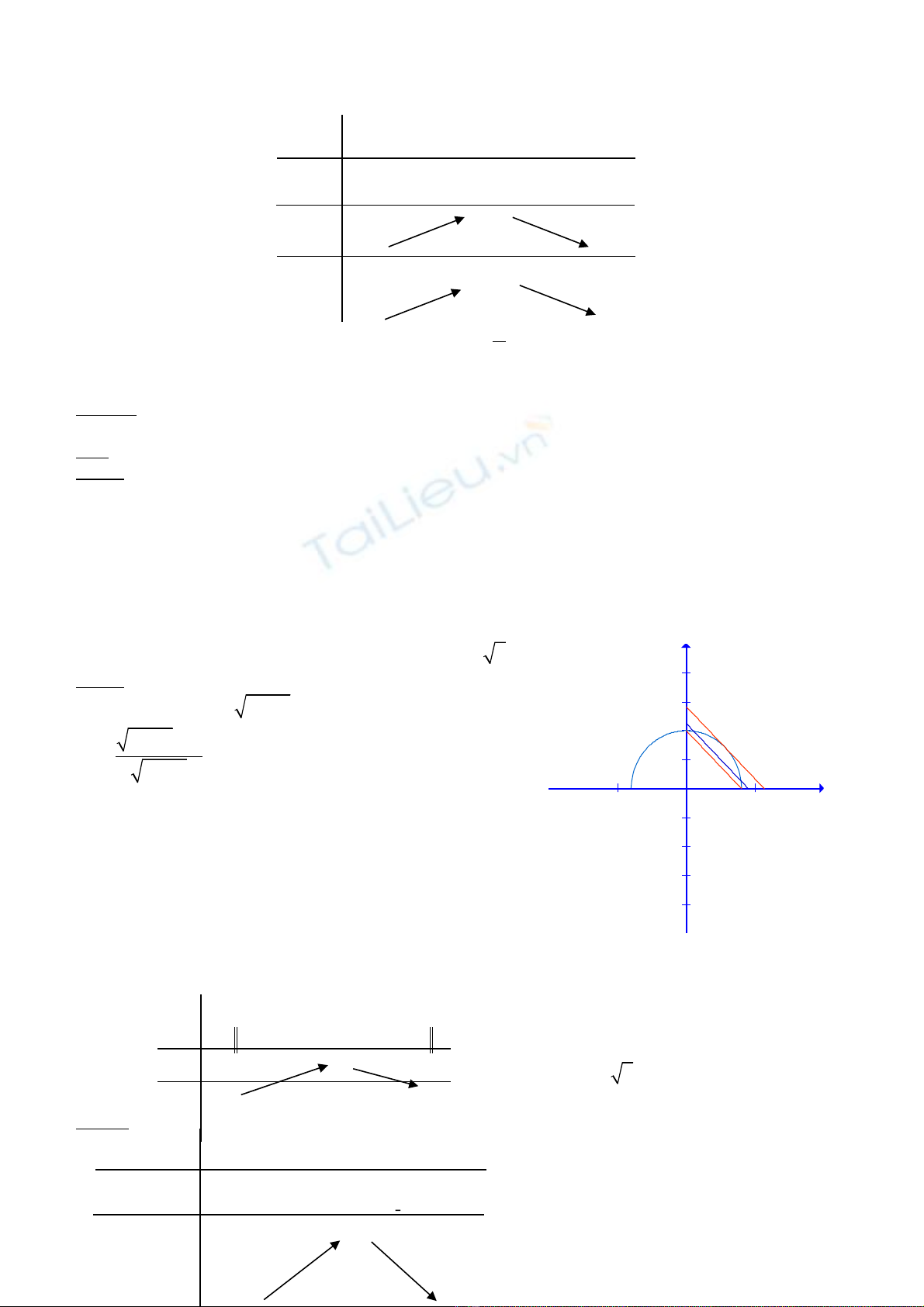
Điêu kiên đê thoa khi cac đ ng (1) va (2) co 2 điêm chung phân biêt. Chu y (1) la n ađ ng tron cô đinh ươ ư ươ
tâm O ban kinh băng 1, năm phia trên Ou; (2) la đ ng thăng thay đôi va luôn song song v i đ ng thăng ươ ơ ươ
v = -u, căt Ov tai tung đô m. Cho m thay đôi, nhân xet răng (1) va (2) co 2 giao điêm phân biêt khi
0
1m m<£
; v i mơ 0 la tung đô giao điêm cua ∆2 v i Ov ( ơ ∆2 la môt vi tri cua đ ng (2) tiêp xuc v i ươ ơ
đ ng (1). ) Dê dang tinh đ c mươ ươ 0 = . Vây
1 2m£ £
.
Cach2 Ph ng phap khao sat ham sô.ươ
Xet ham sô:
2
1 ( 1 1)y x x x= + - - ££
2
2
1
'
1
x x
y
x
- -
=
-
, -1<x<1
y’= 0 ⇔ = x (
0x³
) ⇔ x= .
Bang biên thiên:
x -1 1 Đê thoa đê bai toan đô thi ham trên phai căt
y’ + 0 - đ ng thăng y = m tai 2 điêm phân biêt. Vây:ươ
y
1 2m<£
-1 1
Cach3: Ph ng phap l ng giac.ươ ươ
Đăt x=cosα ,
0x
p
£ £
. Ta đ a vê ph ng trinh cosư ươ α+sinα=m ⇔ sin(α+ ) = . Xet s biên thiên cua ư
ham y = sin(α+ ): ta co y’= cos(α+ ) ; y’= 0 ⇔ x = . Bang biên thiên:
α 0 π
cos(α+ ) + 0
-
sin( α+ ) 1
u
v
1
1D
(1) (2)
-
Ph ng trinh phai co 2 nghiêm ươ α1 va α2 phân biêt; chi khi ≤ <1 ⇔ 1≤ m< .
( α1 ≠ α2 thuôc [0;π ] suy ra x1 = cosα1 ≠ x2 = cosα2 : thoa đê )