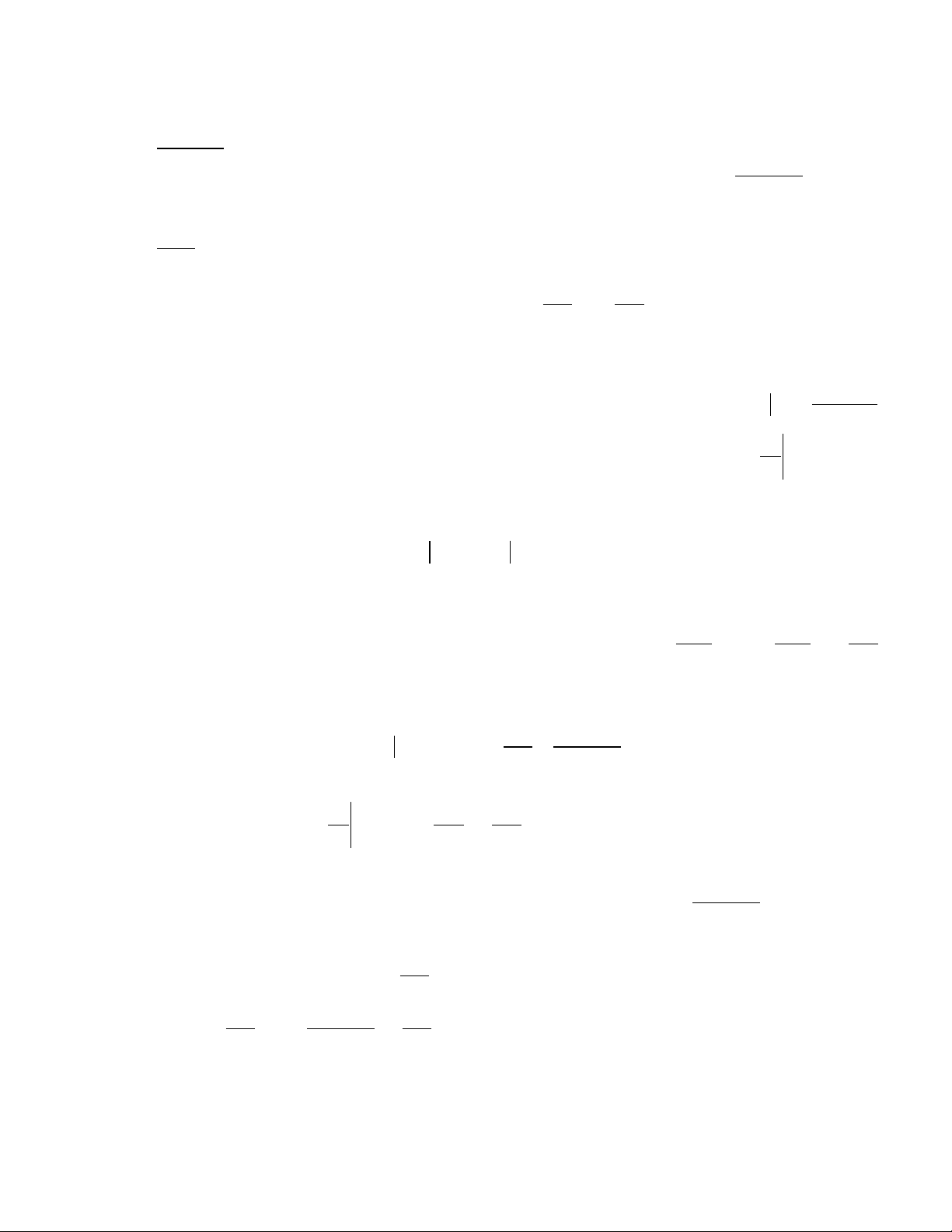
Bµi 1 : X¸c ®Þnh dao ®éng tù do cña d©y h÷u h¹n, g¾n chÆt t¹i c¸c mót x
= 0 vµ x = l, biÕt ®é lÖch ban ®Çu ®îc cho bëi u(x,0) =
2
)(4
l
xlx
(0 x
l) cßn vËn tèc ban ®Çu b»ng 0.
Gi¶i :
Gäi u(x,t) lµ ®é lÖch cña thiÕt diÖn cã hoµnh ®é x ë thêi ®iÓm t.
Ta cã ph¬ng tr×nh dao ®éng cña d©y :
2
2
2
2
2
x
u
a
t
u
(1)
Theo bµi ra, ta cã :
®iÒu kiÖn ban ®Çu :
0
4
0
2
0
t
t
x
u
l
xlx
u
(2)
vµ ®iÒu kiÖn biªn :
0
0
x
u
0
lx
u
(3)
Theo lý thuyÕt, ta cã nghiÖm riªng cña ph¬ng tr×nh (1) tho¶ m·n ®iÒu
kiÖn biªn (3) cã d¹ng : u(x,t) =
l
xk
l
atk
b
l
atk
atxu k
k
k
k
k
sin).sincos(),(
11
(4)
Ta x¸c ®Þnh ak, bk sao cho u(x,t) tho¶ m·n ®iÒu kiÖn ban ®Çu (2)
Thay (4) vµo (2) :
2
1
0
)(4
sin l
xlx
l
xk
au
k
k
t
(5)
0sin
1
0
l
xk
l
ak
b
t
u
k
k
t
(6)
Gi¶i (5) : NhËn thÊy ak lµ hÖ sè trong khai triÓn
2
)(4
l
xlx
thµnh chuçi
Fourier theo hµm sin trong kho¶ng (0, l).
Nh©n 2 vÕ cña (5) víi
råi lÊy tÝch ph©n 2 vÕ tõ 0 l ta cã :
dx
l
xk
l
xlx
dx
l
xk
a
ll
k
sin
)(4
sin
0
2
2
0
(7)
nÕu
nk 2
nÕu
12 nk
VT =
l
k
l
k
l
kl
xk
k
l
x
a
dx
l
xk
adx
l
xk
a
0
0
2
0
sin
222
cos1
sin
=
2
l
a
k
VT =
2
l
a
k
(8)
VP =
l l
dx
l
xk
xdx
l
xk
xl
l0 0
2
2sin.sin..
4
Ta cã : I1 =
k
k
l
l
xk
k
l
l
xk
x
k
l
dx
l
xk
x
l
o
l
o
l
cossincos..sin.
2
22
2
0
I2 =
dx
l
xk
x
k
l
l
xk
x
k
l
dx
l
xk
x
l
l
o
l
cos.
2
cos..sin.
0
2
0
2
I2 = -
33
3
33
33 2
cos
2
cos
k
l
k
k
l
k
k
l
Nªn VP =
33
33
33
33
2
2
coscos
2
cos
4
k
l
k
k
l
k
k
l
k
k
l
l
VP =
k
k
l
k
l
lcos
224
33
3
33
3
2
(9)
Thay (8) (9) vµo (7) ta cã :
ak =
)cos1(
2
.
8
33
3
3
k
k
l
l
=
3
3
33
12
32
0
)cos1(
16
n
k
k
(n=0,1,2...)
Tõ (6) bk = 0
do ®ã, nghiÖm cña bµi to¸n ®· cho :
u(x,t) =
l
xn
l
atn
n
n
)12(
sin
)12(
cos
12
132
0
33
.
Bµi 2 : X¸c ®Þnh dao ®éng tù do cña d©y h÷u h¹n, g¾n chÆt t¹i c¸c mót
x= 0
x = 1 biÕt ®é lÖch ban ®Çu b»ng 0, vËn tèc ban ®Çu ®îc cho bëi :
0
)cos(
)0,( 0cxv
x
t
u
víi v0 lµ h»ng sè d¬ng vµ /2 c l - /2.
nÕu
cx
/2
nÕu
cx
/2
Gi¶i :
Gäi u(x,t) lµ ®é lÖch cña d©y cã hoµnh ®é x ë thêi ®iÓm t .Ta cã ph¬ng
tr×nh dao ®éng cña d©y :
2
2
2
2
2
x
u
a
t
u
trong miÒn (0<x<l , 0<tT)
(1)
tho¶ m·n ®iÒu kiÖn biªn:
0
0
x
u
0
lx
u
(0 tT)
(2)
vµ tho¶ m·n ®iÒu kiÖn ban ®Çu :
0
cos
0
0
0
0
cxv
t
u
u
t
t
(0 x l)
(3)
T¬ng tù bµi 1) ta cã nghiÖm cña ph¬ng tr×nh (1) tho¶ m·n ®iÒu kiÖn biªn
(2) :
u(x,t) =
l
xk
t
l
ak
bt
l
ak
a
k
kk
sinsincos
1
(4)
Tõ ®iÒu kiÖn ban ®Çu ta cã :
00sin
1
0
k
k
k
ta
l
xk
au
(5)
xF
l
xk
l
ak
b
t
u
k
k
t
sin
1
0
NhËn thÊy bk lµ hÖ sè trong khai triÓn F(x) thµnh chuçi Fourier theo hµm
sin trong kho¶ng (0, l)
dx
l
xk
xFdx
l
xk
l
ak
b
ll
k
sinsin
00
2
k
b
2/
2/
sin)cos(
2
c
c
odx
l
xk
cx
ak
v
=
2/
2/
2/
2/
0.1sin.1sin
c
c
c
c
dxcx
l
k
dxcx
l
k
ak
v
=
2/
2/
2/
2/
0
1cos
1
1
1cos
1
1
c
c
c
c
cx
l
k
l
k
cx
l
k
l
k
ak
v
=
cc
l
k
cc
l
k
l
k
ak
v
2
1cos
2
1cos
1
1
0
nÕu
cx
/2
nÕu
cx
/2
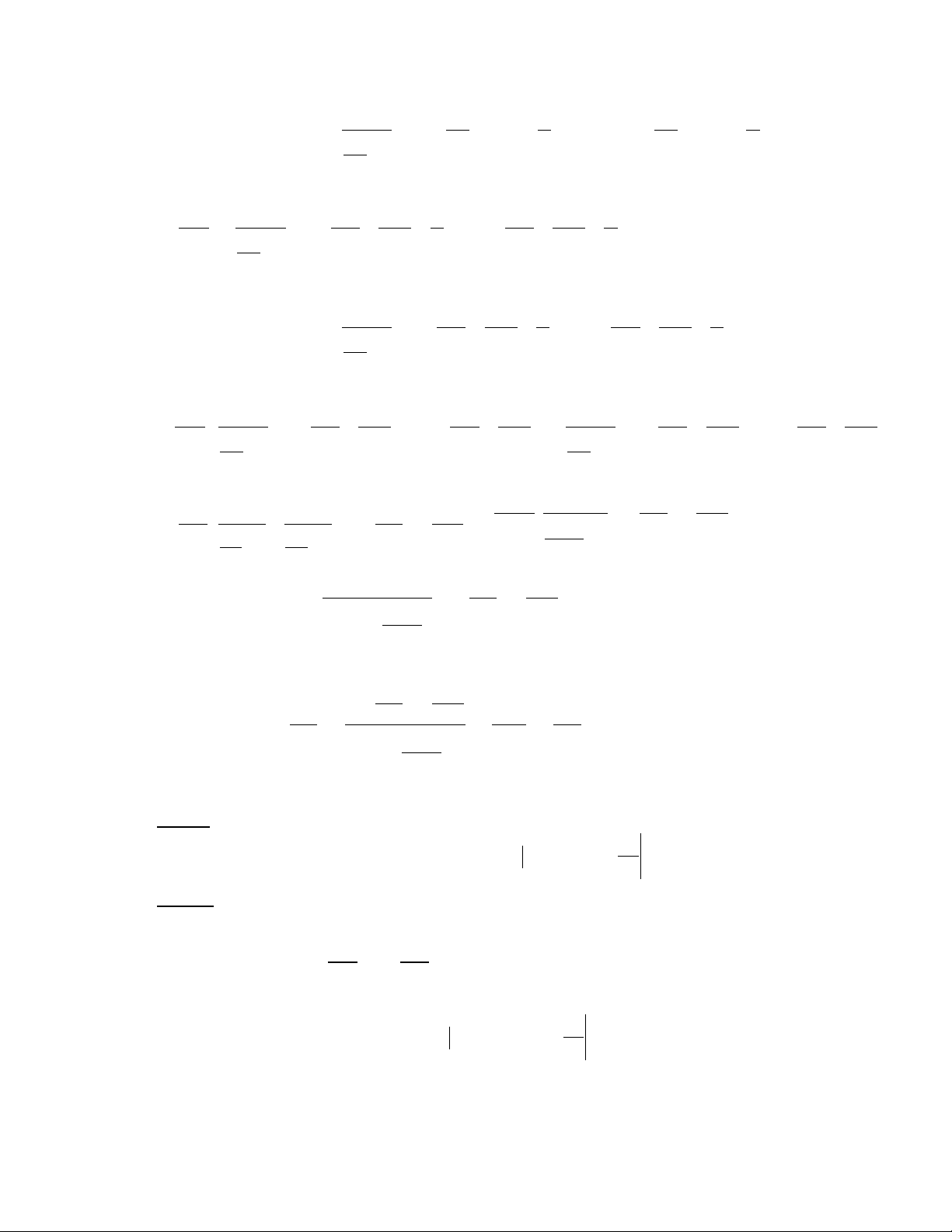
cc
l
k
cc
l
k
l
k2
1cos
2
1cos
1
1
=
22
cos
22
cos
1
122
0
l
k
l
ck
l
k
l
ck
l
k
ak
v
22
cos
22
cos
1
122
l
k
l
ck
l
k
l
ck
l
k
l
k
l
ck
l
k
l
ck
l
k
l
k
l
ck
l
k
l
ck
l
k
ak
v
2
sin
2
sin
1
1
2
sin
2
sin
1
12222
0
=
l
k
l
ck
l
k
l
k
ak
v
2
cossin2
1
1
1
1
2
0
=
l
k
l
ck
l
k
ak
v
2
cos.sin
1
1
.
4
2
2
22
0
bk =
l
k
l
ck
l
k
ak
v
2
cos.sin.
1
4
2
2
22
0
Do ®ã nghiÖm cña bµi to¸n ®· cho lµ :
u(x,t) =
.sinsin
1
2
cos.sin
.
4
1
2
22
2
0
l
xk
l
atk
l
k
k
l
k
l
ck
a
v
k
Bµi 3 : X¸c ®Þnh dao ®éng däc cña thanh nÕu 1 mót g¾n chÆt cßn 1 mót
tù do, biÕt c¸c ®iÒu kiÖn ban ®Çu :
)(
0xfu t
,
)(
0
xF
t
u
t
Gi¶i :
Gäi u(x,t) lµ ®é lÖch cña thiÕt diÖn cã hoµnh ®é x ë thêi ®iÓm t
Ph¬ng tr×nh :
2
2
2
2
2
x
u
a
t
u
(1)
Tho¶ m·n ®iÒu kiÖn ®Çu :
)(
0xfu t
,
)(
0
xF
t
u
t
(2)
Tho¶ m·n ®iÒu kiÖn biªn :
0
0
x
u
,
0
lx
x
u
(3)
NghiÖm cña ph¬ng tr×nh cã d¹ng : U(x,t) = X(x).T(t)
(4)
Tõ (1) vµ (4) ta cã :
)6(0"
)5(0"
2TaT
XX
Tõ (3)&(4) X(0) = 0 ; X’(l) = 0
(7)
Gi¶i (5) :
* = - c2 X(x) = c1.e-cx + c2.ecx nªn theo (7) :
X(x) = c1 + c2 = 0 c1 + c2 = 0 c1 = 0
X’(l) = -c.c1.e-cl + c.c2.ecl = 0 c2.ecl – c1e-cl = 0 c2 = 0 (lo¹i)
* = 0 X(x) = c1 + c2x Theo (7) :
0'
00
2
1
clX
cX
(lo¹i)
* = c2 X(x) = c1cos cx + c2sin cx
Tõ (7)
0cos)('
0)0(
2
1
clcclX
cX
§Ó c2 = Ak cos cl = 0
kcl 2
l
k
c2
12
=
2
2
12
l
k
NghiÖm cña ph¬ng tr×nh (5) tho¶ m·n ®iÒu kiÖn biªn (7) lµ :
l
xk
AxX kk 2
12
sin
Gi¶i (6) :
l
atk
D
l
atk
BtT kkk 2
12
sin
2
12
cos
Nªn nghiÖm riªng cña ph¬ng tr×nh (1) lµ :
l
xk
l
atk
b
l
atk
atxu
k
kk 2
12
sin
2
12
sin
2
12
cos),(
0
(8)
Tõ (2) ta cã :
)(
2
12
sin
0
0xf
l
xk
au k
k
t
(9)