Biên s anọ: Tr n Văn Hùngầ - THPT Nguy n B nh Khiêmễ ỉ
GI I TÍCH 12ẢEmail: tranhung18102000@yahoo.com
TI M C N, KH O SÁT HÀM S VÀ CÁC BÀI TOÁN LIÊN QUANỆ Ậ Ả Ố
A. Tóm t t lý thuy tắ ế
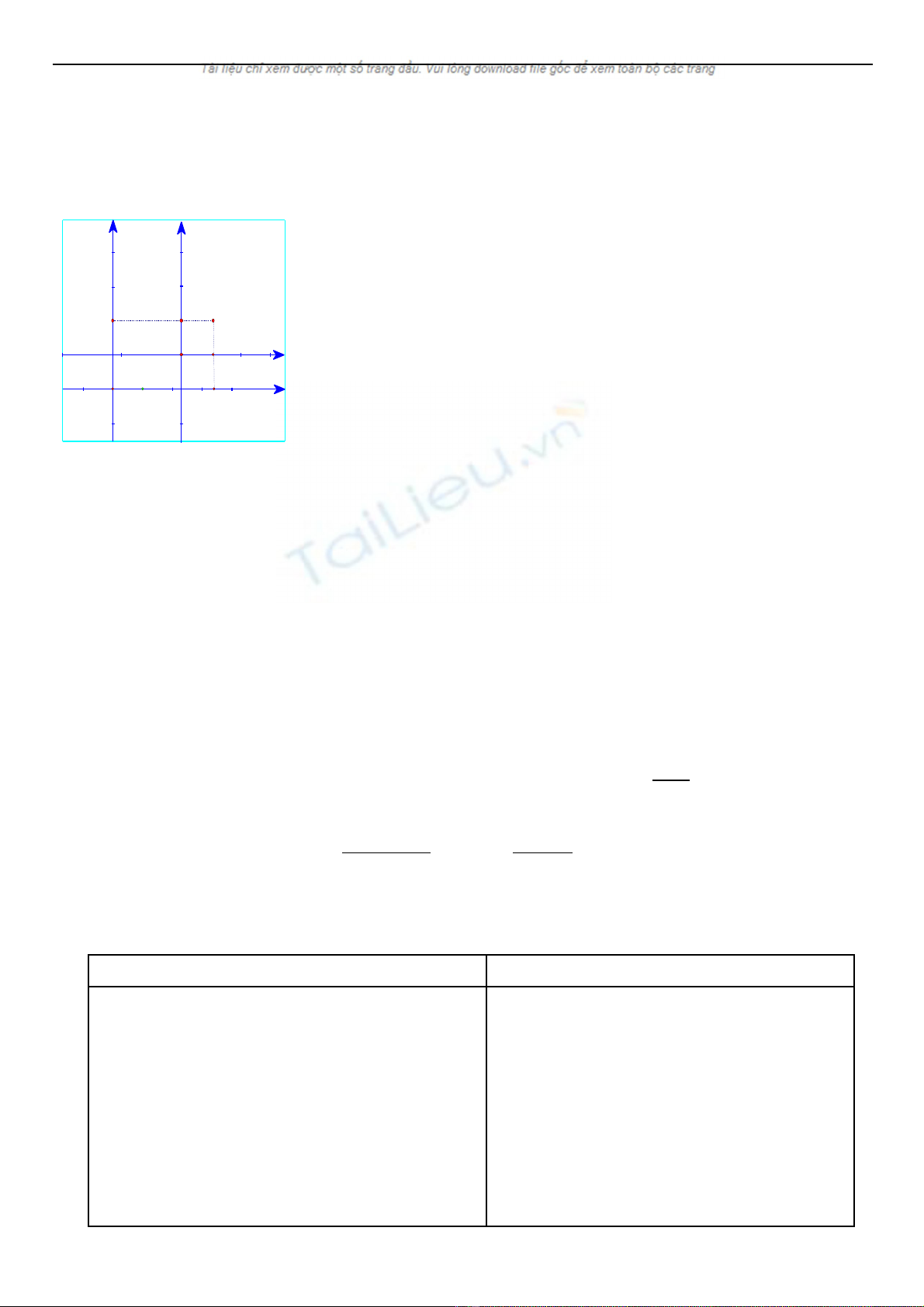
Đ TH HÀM S VÀ PHÉP T NH TI N H TR C TO ĐỒ Ị Ố Ị Ế Ệ Ụ Ạ Ộ
1. Trong mp(Oxy) cho đi m I(xể0;y0) . G i IXY là h to đ m i có g cọ ệ ạ ộ ớ ố
là I và hai tr c IX,IY theo th t có cùng vect đ n v ụ ứ ự ơ ơ ị
,i j
rr
v i hai tr c Ox,ớ ụ
Oy M là đi m b t kì c a mp, gi s M(x;y)/(Oxy) và M(X;Y)/(IXY) Tacó:ể ấ ủ ả ử
0
0
xXx
y Y y
= +
=
== +
=
2. Ph ng trình c a đ ng cong đ i v i h to đ m i:ươ ủ ườ ố ớ ệ ạ ộ ớ
Gi s (C) là đ th hàm s ả ử ồ ị ố y = f(x) đ i v i h Oxy . T nh ti n h tr cố ớ ệ ị ế ệ ụ
Oxy theo vec t ơ
OI
uur
v i ớI(x0;y0) theo công th c đ i tr c ứ ổ ụ
0
0
x X x
y Y y
= +
=
== +
=
ta có
ph ng trình c a (C) trong h to đ IXY là: Y = (X+xươ ủ ệ ạ ộ 0) – y0
TI M C NỆ Ậ
1) Ti m c n ngang: ệ ậ Đ ng th ng y = yườ ẳ 0 đ c g i là ti m c n ngang c a đ th hàm s ượ ọ ệ ậ ủ ồ ị ố
( )y f x=
n u ế
0
lim ( )
x
f x y
f+y
=
ho cặ
0
lim ( )
x
f x y
f−y
=
2) Ti m c n đ ng: ệ ậ ứ Đ ng th ng x = xườ ẳ 0 đ c g i là ti m c n đ ng c a đ th hàm s ượ ọ ệ ậ ứ ủ ồ ị ố
( )y f x=
n u ít nh t m t trong các đi u ki n sau đ c tho mãn:ế ấ ộ ề ệ ượ ả
0 0
0 0
lim ( ) ; lim ( )
lim ( ) ; lim ( )
x x x x
x x x x
f x f x
f x f x
− +
− +
−+
−+
= +f= +;
= −f= −;
3) Ti m c n xiên: ệ ậ Đu ng th ng y= ax+b (aờ ẳ
0) đ c g i là đ ng ti m c n xiên c a đ th hàm sượ ọ ườ ệ ậ ủ ồ ị ố
( )y f x=
n uế
lim [ ( ) (ax+b)] 0
x
f x
f+m
− =
ho c ặ
lim [ ( ) (ax+b)] 0
x
f x
f−m
− =
- Cách tìm các h s a, b c a ti m c n xiên y = ax + b: ệ ố ủ ệ ậ
( ) ( )
( )
lim ; b= lim [ ( ) ax]
l+m−;+ −=
= −
x
f x
a f x
x
.
- Đ tìm ti m c n xiên c a hàm s h u t ta th c hi n phép chia đ vi t l i hàm s :ể ệ ậ ủ ố ữ ỉ ự ệ ể ế ạ ố
2
ax bx c r
px q (a.a ' 0, r 0)
a ' x b ' a ' x b '
+ + = + +b'
+ +
KH O SÁT HÀM SẢ Ố
Các b c kh o sát hàm s :ướ ả ố
Các b c kh o sát hàm đa th cướ ả ứ Các b c kh o sát hàm h u tướ ả ữ ỷ
1. T p xác đ nhậ ị
2. S bi n thiênự ế
- Gi i h n t i vô c cớ ạ ạ ự
- Chi u bi n thiên, c c trề ế ự ị
- B ng bi n thiênả ế
3. Đ thồ ị
- Đi m u nể ố
- Đi m đ c bi tể ặ ệ
- Đ thồ ị
1. T p xác đ nhậ ị
2. S bi n thiênự ế
- Gi i h n, ti m c n ớ ạ ệ ậ
- Chi u bi n thiên, c c trề ế ự ị
- B ng bi n thiênả ế
3. Đ thồ ị
- Tâm đ i x ngố ứ
- Giá tr đ c bi tị ặ ệ
- Đ thồ ị
1
x
y
X
Y
Y
X
M
1
y
x
Biên s anọ: Tr n Văn Hùngầ - THPT Nguy n B nh Khiêmễ ỉ
GI I TÍCH 12ẢEmail: tranhung18102000@yahoo.com
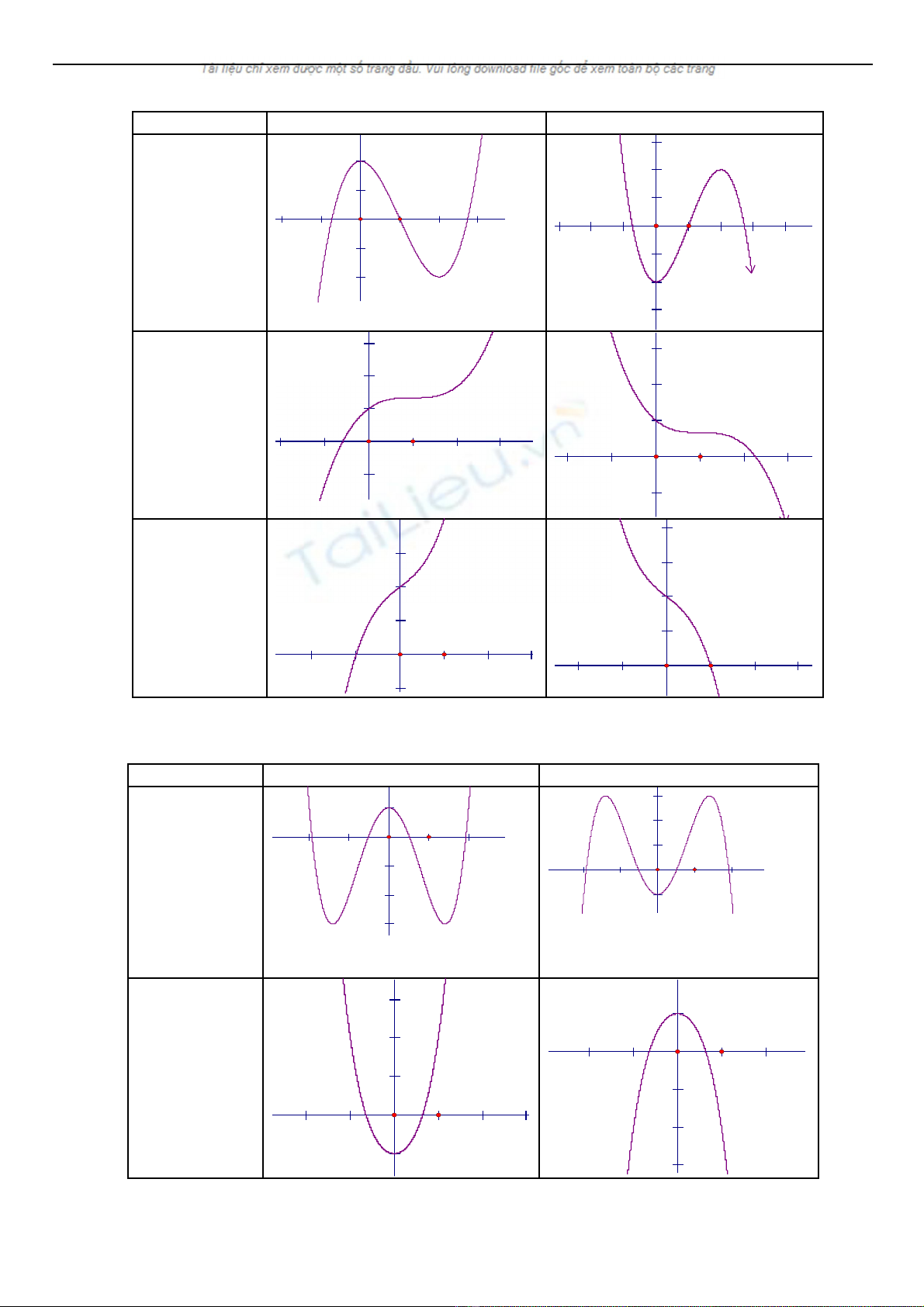
Hàm s b c 3:ố ậ y = ax3 + bx2 + cx + d (a ≠ 0)
a > 0 a < 0
Pt y’ = 0 có hai
nghi m phânệ
bi t.ệ
2
-2
O
2
-2
Pt y’ = 0 có
nghi m képệ
2
2
Pt y’ = 0 vô
nghi mệ
2
4
2
Hàm s trùng ph ng:ố ươ y = ax4 + bx2 + c (a ≠ 0)
a > 0 a < 0
Pt y’ = 0 có ba
nghi m phânệ
bi tệ
-2
2
Pt y’ = 0 có
m t nghi mộ ệ
2
-2
2
Biên s anọ: Tr n Văn Hùngầ - THPT Nguy n B nh Khiêmễ ỉ
GI I TÍCH 12ẢEmail: tranhung18102000@yahoo.com
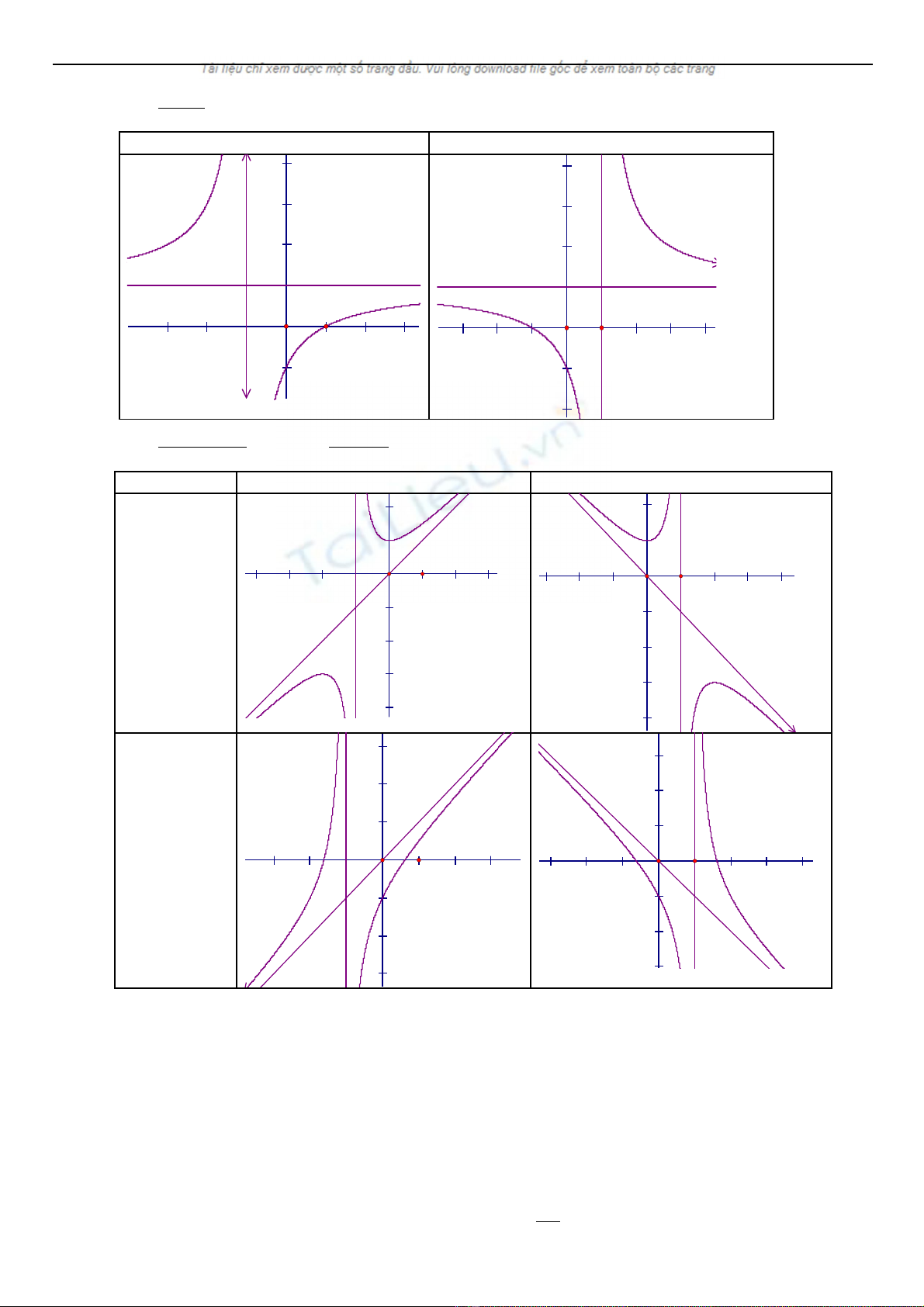
Hàm s y = ố
ax b (c 0, ad bc 0)
cx d
++ −d
+
D = ad – bc > 0 D = ad – bc < 0
4
2
4
2
-2
Hàm s y = ố
2
ax bx c r
px q (a.a ' 0, r 0)
a ' x b ' a ' x b '
+ + = + +b'
+ +
a.a’ > 0 a.a’ < 0
Pt y’ = 0 có
hai nghi mệ
phân bi tệ
2
-2
-4
O
2
-2
-4
O
Pt y’ = 0 vô
nghi mệ
2
-2
O
2
-2
O
CÁC BÀI TOÁN CÓ LIÊN QUAN
1. Bi n lu n s giao đi m c a 2 đ ng (C): y = f(x) và (C’): y = g(x)ệ ậ ố ể ủ ườ
S giao đi m c a hai đ ng (Cố ể ủ ườ 1) y= f(x) và (C2) y=g(x) là s nghi m c a ph ng trình hoành đố ệ ủ ươ ộ
giao đi m c a (Cể ủ 1), (C2): f(x) = g(x) (1)
2. S ti p xúc c a hai đ ng cong:ự ế ủ ườ
Hai đ ng cong (Cườ 1), (C2) ti p xúc v i nhau khi ch khi h sau có nghi m: ế ớ ỉ ệ ệ
( ) ( )
'( ) '( )
f x g x
f x g x
=
=
==
=
Vi t PTTT c a đ th (C) hàm s y =f(x)ế ủ ồ ị ố
Bài toán 1: Vi t ph ng trình ti p tuy n c a (C): y = f(x) ế ươ ế ế ủ t iạ M0(x0;y0) ∈ (C).
Tìm các thành ph n ch a có xầ ư 0, y0, f’(x0) thay vào y – y0 = f’(x0)
( )
0
x x−
3
Biên s anọ: Tr n Văn Hùngầ - THPT Nguy n B nh Khiêmễ ỉ
GI I TÍCH 12ẢEmail: tranhung18102000@yahoo.com
Bài toán 2: Vi t pttt c a (C): y = f(x) bi t h s góc k c a ti p tuy n.ế ủ ế ệ ố ủ ế ế
(hay: bi t ti p tuy n song song, vuông góc v i 1 đ ng th ng (D) )ế ế ế ớ ườ ẳ
- L p ph ng trình f’(x) = k ậ ươ ⇒ .. ⇒ x = x0 ( hoành đ ti p đi m)ộ ế ể
- Tìm y0 và thay vào d ng y = k(x – xạ0) + y0. ta có k t quế ả
Bài toán 3: Vi t pttt c a (C): y = f(x) bi t ti p tuy n ế ủ ế ế ế đi qua hay xu t phát tấ ừ A(xA;yA)
- Vi t pt đ ng th ng (d) đi qua A và có h s góc k: y – yế ườ ẳ ệ ố A = k(x – xA) (1)
- (d) là ti p tuy n c a (C) khi ch khi h sau có nghi m:ế ế ủ ỉ ệ ệ
A A
f (x) k(x x ) y
f '(x) k(*)
= − +
=
==
=
- Gi i ptả
( ) '( )( )
A A
f x f x x x y= − +
tìm x và thay vào (*) tìm k , thay vào (1) ta có k t qu .ế ả
B. Các ví d và bài t pụ ậ
1. Cho (C) : y = x3 – 6x2 + 9x – 1.Vi t ph ng trình ti p tuy n c a (C) :ế ươ ế ế ủ
a) T i đi m u n c a (C).ạ ể ố ủ b) T i đi m có tung đ b ng -1ạ ể ộ ằ
c) Song song v i đ ng th ng dớ ườ ẳ 1 : y = 9x – 5. d) Vuông góc v i đ ng th ng dớ ườ ẳ 2 : x + 24y = 0.
2. Vi t ph ng trình ti p tuy n v i đ th (C).ế ươ ế ế ớ ồ ị
a) y = x3 – 3x + 2 đi qua đi m A(1 ; 0) b) y = ể
2
3
3
2
124 +− xx
đi qua đi m A(0 ; ể
)
2
3
.
c) y =
2
2
−
+
x
x
đi qua đi m A(-6 ; 5) ểd) y =
2
54
2
−
+−
x
xx
đi qua đi m A(2 ; 1).ể
3. Tìm m đ đ th hàm s y = (x – 1) (xể ồ ị ố 2 + mx + m) c t tr c hòanh t i ba đi m phân bi tắ ụ ạ ể ệ
4. Tìm m đ đ th hàm s y = ể ồ ị ố
mxx +−
3
3
1
c t tr c hòanh t i ba đi m phân bi t.ắ ụ ạ ể ệ
5. Tìm m đ đ th hàm s y = xể ồ ị ố 4 – 2(m + 1)x2 + 2m + 1 không c t tr c hòanh.ắ ụ
6. Tìm m đ đ th hàm s y = xể ồ ị ố 4 – 2x2 – (m + 3) c t tr c hòanh t i 4 đi m phân bi t.ắ ụ ạ ể ệ
7. Tìm m đ đ ng th ng y = mx + 2m + 2 c t đ th hàm s y = ể ườ ẳ ắ ồ ị ố
1
12
+
−
x
x
a) T i hai đi m phân bi t.ạ ể ệ
b) T i hai đi m thu c hai nhánh c a đ th .ạ ể ộ ủ ồ ị
8. Tìm m đ đ ng th ng y = mx + m + 3 c t đ th hàm s y = ể ườ ẳ ắ ồ ị ố
1
332 2
+
++
x
xx
a) T i hai đi m phân bi t .ạ ể ệ
b) T i hai đi m thu c hai nhánh c a đ th .ạ ể ộ ủ ồ ị
9. Tìm m đ đ ng th ng đi qua đi m A(-1;-1) và có h s góc là m c t đ th hàm s y = ể ườ ẳ ể ệ ố ắ ồ ị ố
12
2
+
+
x
x
a) T i hai đi m phân bi t.ạ ể ệ
b) T i hai đi m thu c cùng m t nhánh.ạ ể ộ ộ
10. Ch ng minh r ng (P) : y = xứ ằ 2 -3x – 1 ti p xúc v i (C) : ế ớ
1
32
2
−
−+−
x
xx
.
11. Tìm m sao cho (Cm) : y =
1
2
−
+
x
mx
ti p xúc v i đ ng th ng y = -x + 7.ế ớ ườ ẳ
12. a) V đ th hàm s y = ẽ ồ ị ố
)1x(2
3x4x2
2
−
−−
b) Tìm m đ ptể : 2x2 – 4x – 3 + 2m|x - 1| = 0 có 2 nghi m phânệ
bi t.ệ
13. Cho hàm s y = xố3 + 3x2 – 4
a) Kh o sát s bi n thiên và v đ th (C) c a hàm s .ả ự ế ẽ ồ ị ủ ố
b) Vi t ph ng trình ti p tuy n c a đ th (C) t i đi m Mế ươ ế ế ủ ồ ị ạ ể 0(-1; -2)
c) Ch ng minh r ng đi m u n c a (C) là tâm đ i x ng c a nó.ứ ằ ể ố ủ ố ứ ủ
14. Cho hàm s y = -xố3 + 3x + 1.
a) Kh o sát s bi n thiên và v đ th (C) c a hàm s .ả ự ế ẽ ồ ị ủ ố
b) D a vào đ th (C), bi n lu n theo m s nghi m c a ph ng trình xự ồ ị ệ ậ ố ệ ủ ươ 3 – 3x + m = 0.
c) Vi t ph ng trình ti p tuy n c a đ th (C) t i đi m có hòanh đ xế ươ ế ế ủ ồ ị ạ ể ộ 0 = 1.
4
Biên s anọ: Tr n Văn Hùngầ - THPT Nguy n B nh Khiêmễ ỉ
GI I TÍCH 12ẢEmail: tranhung18102000@yahoo.com
15. Cho hàm s y = xố3 – 6x2 + 9x + 1
a) Kh o sát s bi n thiên và v đ th (C) c a hàm s .ả ự ế ẽ ồ ị ủ ố
b) Vi t ph ng trình ti p tuy n c a (C) bi t ti p tuy n đó vuông góc v i đ ng th ng ế ươ ế ế ủ ế ế ế ớ ườ ẳ
12
24
y x= − +
c) Vi t ph ng trình đ ng th ng đi qua hai đi m c c tr c a hàm s .ế ươ ườ ẳ ể ự ị ủ ố
16. Cho hàm s y = ố
2
3
3
2
2
4+− x
x
a) Kh o sát s bi n thiên và v đ th (C) c a hàm s .ả ự ế ẽ ồ ị ủ ố
b) Bi n lu n theo m s nghi m c a ph ng trình: ệ ậ ố ệ ủ ươ
4 2
6 3 0x x m- + - =
c) Vi t ph ng trình ti p tuy n c a (C) bi t ti p tuy n đi qua đi m A(0 ; ế ươ ế ế ủ ế ế ế ể
)
2
3
17. Cho hàm s ố
4 2
6 5y x x= - + -
a) Kh o sát s bi n thiên và v đ th (C) c a hàm s .ả ự ế ẽ ồ ị ủ ố
b) Tìm m đ đ ng th ng y = m c t đ th (C) t i 4 đi m phân bi t.ể ườ ẳ ắ ồ ị ạ ể ệ
c) Vi t ph ng trình ti p tuy n c a (C) t i đi m Mế ươ ế ế ủ ạ ể 0(1 ; 0).
18. Cho hàm s y = ố
1
1
−
+
x
x
.
a) Kh o sát s bi n thiên và v đ th (H) c a hàm s .ả ự ế ẽ ồ ị ủ ố
b) Vi t ph ng trình ti p tuy n c a (H) t i đi m Mế ươ ế ế ủ ạ ể 0(2 ; 3).
c) Vi t ph ng trình ti p tuy n c a (H) bi t ti p tuy n song song v i đ ng th ng y = -2x + 1ế ươ ế ế ủ ế ế ế ớ ườ ẳ
19. Cho hàm s y = ố
1
33
2
+
++
x
xx
a) Kh o sát s bi n thiên và v đ th (C) c a hàm s .ả ự ế ẽ ồ ị ủ ố
b) Bi n lu n theo m só nghi m c a ph ng trình: xệ ậ ệ ủ ươ 2 + (3 – m)x + 3 – m = 0.
c) Tìm đi m trên (C) cách đ u hai tr c t a đ .ể ề ụ ọ ộ
20: Cho hàm s y = ố
x
xx
−
−+
1
1
2
a) Kh o sát s bi n thiên và v đ th (C) c a hàm s .ả ự ế ẽ ồ ị ủ ố
b) Vi t ph ng trình ti p tuy n c a (C) t i đi m Mế ươ ế ế ủ ạ ể 0(0, -1).
c) Ch ng minh r ng không có ti p tuy n nào c a (C) song song v i ti m c n xiên c a (C)ứ ằ ế ế ủ ớ ệ ậ ủ
21. Cho hàm s y = ố
1
)2( 2
−
−
x
x
a) Kh o sát s bi n thiên và v đ th (C) c a hàm s .ả ự ế ẽ ồ ị ủ ố
b) G i (d) là đ ng th ng điqua A(-1 ; 0) có h s góc là m . Tìm m đ (d) c t (C) t i hai đi m phânọ ườ ẳ ệ ố ể ắ ạ ể
bi t. ệ
c) CM: Tích các kh ang cách t m t đi m M trên (C) đ n hai ti m c n c a (C) là m t s không đ i.ỏ ừ ộ ể ế ệ ậ ủ ộ ố ổ
22. Cho hàm s y = ố
1
)2(
2
+
−++
x
mxmx
có đ th là (Cồ ị m).
a) Xác đ nh m sao cho ti m c n xiên c a (Cị ệ ậ ủ m) đ nh trên hai tr c t a đ m t tam giác có di n tích b ng 8.ị ụ ọ ộ ộ ệ ằ
b) Kh o sát s bi n thiên và v đ th (C) c a hàm s khi m = 3ả ự ế ẽ ồ ị ủ ố
c) Xác đ nh k đ cho đ ng th ng y = k c t (C) t i hai đi m phân bi t E, F sao cho đ an EF là ng nị ể ườ ẳ ắ ạ ể ệ ọ ắ
nh t.ấ
23. Cho (Cm) có ph ng trình y = xươ 4 – 2(m+1)x2 +2m + 1
a) Tìm đi m c đ nh c a h (Cm)ể ố ị ủ ọ
b) Đ nh m đ đ th hàm s c t tr c hoành t i 4 đi m có hoành đ l p thành c p s c ng.ị ể ồ ị ố ắ ụ ạ ể ộ ậ ấ ố ộ
24. Cho hàm s y = xố3 – 3ax2 + 4a3. Tìm a đ đ ng th ng y = x c t đ th hàm s t i ba đi m A, B, C saoể ườ ẳ ắ ồ ị ố ạ ể
cho AB = AC.
25. Cho hàm s y = xố3 - 3x2 + 2 có đ th (C). Tìm trên đ ng th ng y = -2 các đi m mà t đó có th kồ ị ườ ẳ ể ừ ể ẻ
đ c hai ti p tuy n t i (C) và vuông góc v i nhauượ ế ế ớ ớ
26. Cho hàm s y = xố3 - 3x2 (C). Tìm trên (C) các đi m mà t đó có th k đ c m t ti p tuy n t i (C).ể ừ ể ẻ ượ ộ ế ế ớ
5