
Khảo sát hàm số cho bởi phương trình tham số
Tích phân bất định Tiệm cận xiên
Tính lồi lõm và điểm uốn của đồ thị hàm số
Các bước khảo sát và vẽ đồ thị hàm số
1Tìm tập xác định;
2Xác định tính chẵn lẻ và tính tuần hoàn;
3Tính các giới hạn và xác định các tiệm cận;
4Xác định các khoảng đơn điệu;
5Xác định các giá trị cực đại và cực tiểu;
6Xác định các khoảng lồi, lõm và xác định điểm uốn;
7Xác định các điểm đặc biệt và vẽ đồ thị.
TS. Đào Huy Cường (Bộ môn Toán Ứng Dụng) Giải tích 1 (Calculus 1)
Khảo sát hàm số cho bởi phương trình tham số
Tích phân bất định Tiệm cận xiên
Tính lồi lõm và điểm uốn của đồ thị hàm số
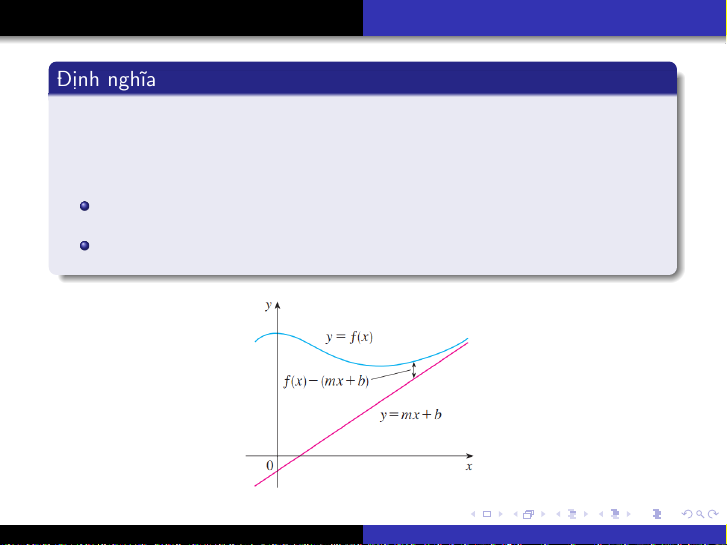
Định nghĩa
Đường thẳng y=mx +b(với m6=0) được gọi là một tiệm cận
xiên (slant asymptote) của đường cong y=f(x)nếu ít nhất một
trong các mệnh đề sau đây là đúng:
lim
x→∞[f(x)−(mx +b)] = 0.
lim
x→−∞[f(x)−(mx +b)] = 0.
TS. Đào Huy Cường (Bộ môn Toán Ứng Dụng) Giải tích 1 (Calculus 1)
Khảo sát hàm số cho bởi phương trình tham số
Tích phân bất định Tiệm cận xiên
Tính lồi lõm và điểm uốn của đồ thị hàm số
Định lý
Nếu lim
x→∞
f(x)
x=mvà lim
x→∞[f(x)−mx] = b, thì đường thẳng
y=mx +blà tiệm cận xiên của đường cong y=f(x).
Tương tự với x→ −∞.
TS. Đào Huy Cường (Bộ môn Toán Ứng Dụng) Giải tích 1 (Calculus 1)
Khảo sát hàm số cho bởi phương trình tham số
Tích phân bất định Tiệm cận xiên
Tính lồi lõm và điểm uốn của đồ thị hàm số
Ví dụ
Cho hàm số y=f(x)xác định bởi phương trình tham số
x=t−2
t,
y=t2+1
t+1,
t>0.
Xác định tiệm cận của đồ thị hàm số.
TS. Đào Huy Cường (Bộ môn Toán Ứng Dụng) Giải tích 1 (Calculus 1)



























