CÁC D NG TOÁN V ĐO HÀM TH NG G PẠ Ề Ạ ƯỜ Ặ
A. CÁC D NG TOÁN TH NG G P : Ạ ƯỜ Ặ
1. Tìm đo hàm theo đnh nghĩa ạ ị
1.1.Ph ng pháp : ươ Đ tìm đo hàm theo đnh nghĩa ta có 2 cách sau :ể ạ ị
Cách 1 : Theo quy t cắ
oB c 1 :ướ Cho
x
m t s gia ộ ố
x
∆
và tìm s gia ố
y∆
tìm
( ) ( )
y f x x f x∆ = + ∆ −
.
L p t s ậ ỉ ố
y
x
∆
∆
oB c 2 :ướ Tìm gi i h n ớ ạ
0
lim
x
y
x
∆
∆
∆
Cách 2 : Áp d ng công th c: ụ ứ
( )
( )
( )
0
0
0
0
' lim
x x
f x f x
f x x x
−
=−
.
1.2.Các ví d minh h a :ụ ọ
Ví d 1.ụ Tìm đo hàm c a các hàm s sau theo đnh nghĩa t i các đi m đã ch ra:ạ ủ ố ị ạ ể ỉ
a)
( )
3
2 1f x x x= − +
t i ạ
02x=
; b)
t i ạ
01x=
.
Ví d 2.ụ Tìm đo hàm c a các hàm s sau theo đnh nghĩa t i các đi m đã ch ạ ủ ố ị ạ ể ỉ
ra:
a)
( )
3
3 4f x x= +
t i ạ
03x=
; b)
( )
3
khi
khi
2 2
10 16 2
x x x
f x x x
−
=− <
t i ạ
02x=
.
Ví d 3.ụ Tìm đo hàm c a các hàm s sau theo đnh nghĩa : ạ ủ ố ị
a)
3 2
2 1y x x= − +
; b)
( )
2
3 2y f x x x= = − +
.
1.3.Bài t p áp d ng :ậ ụ
Bài 1.Tìm đo hàm c a các hàm s sau theo đnh nghĩa t i các đi m đã ch ra : ạ ủ ố ị ạ ể ỉ
a)
( )
2
3 1f x x x= − +
t i ạ
03x=
; b)
( )
2
2f x x x= −
t i ạ
01x=
;
c)
( )
2
3 3
2
x x
f x x
− +
=+
t i ạ
04x=
; d)
t i ạ
04
x
π
=
;
Bài 2.Xét tính liên t c và s t n t i đo hàm và tính đo hàm c a các hàm s sau ụ ự ồ ạ ạ ạ ủ ố
đây trên
ﾡ
.
a)
( )
2
khi
khi
4 3 1
1
3 5 1
x x x
f x x
x x
− +
>
=−
−
; b)
( )
2
3
khi
khi
2 0
0
x a x
f x
x bx x
+
=− + >
;
c)
( )
23 2f x x x= − +
; d)
( )
5
f x x=
.
Bài 3.Tìm đo hàm c a các hàm s sau theo đnh nghĩa : ạ ủ ố ị
a)
( )
3 2
3 2 1f x x x x= − + +
; b)
( )
3
f x x=
;
c)
( )
1
1
x
f x x
−
=+
; d)
( )
1
sin
f x x
=
;
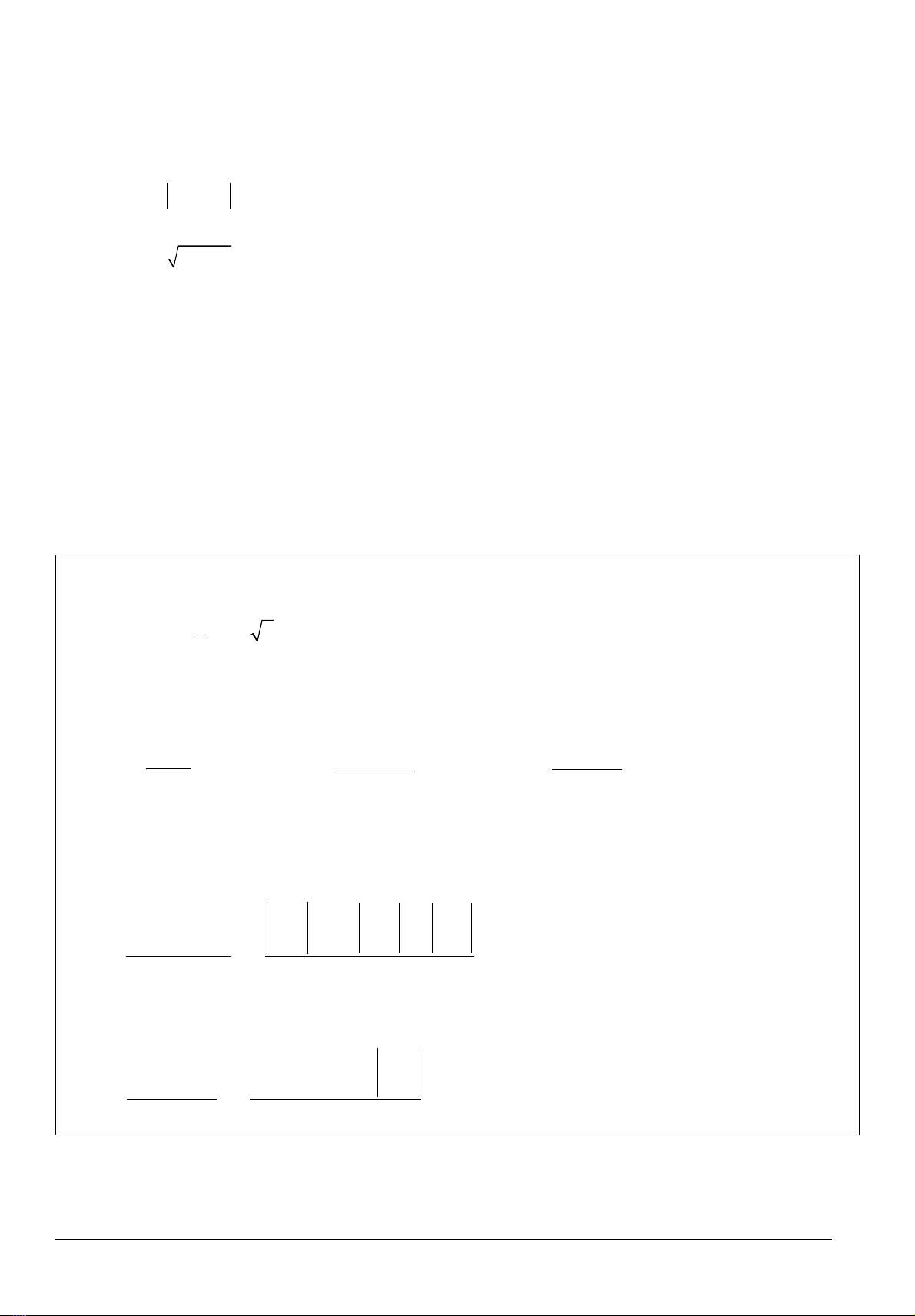
Bài 4.Tìm đo hàm c a các hàm s sau theo đnh nghĩa : ạ ủ ố ị
a)
( )
3 2
4f x x x= −
; b)
( )
khi
khi
sin cos 0
2 1 0
x x x
f x x x
+ >
=+
;
c)
( )
2
4
3f x x x= +
; d)
( ) ( )
3
tan 2 1f x x= +
.
Bài 5.Có bao nhiêu ti p tuy n c a ế ế ủ
( )
3 2
: 3 6 5C y x x x= − + −
có h s góc âm ?ệ ố
.
1.4.Các ví d minh h a :ụ ọ
Ví d 4.ụTìm đo hàm c a các hàm s sau : ạ ủ ố
a)
= − + −
4 3
1
2 2 5
3
y x x x
; b)
= − −
3 2
( 2)(1 )y x x
.
Ví d 5.ụTìm đo hàm c a các hàm s sau : ạ ủ ố
a)
+
=−
2 1
1 3
x
yx
; b)
− +
=−
23 3
1
x x
yx
; c)
+ −
=− +
2
2
1
1
x x
y
x x
.
Ví d 6.ụCh ng minh các công th c t ng quát sauứ ứ ổ
a)
( )
2
21 1 1 1 1 1
2 2
2
1 1 1 1 1 1
2
a b a c b c
x x
a b a c b c
ax bx c
a x b x c a x b x c
+ +
� �
+ + =
� �
� �
+ +
� � + +
; (
1 1 1
, , , , ,a b c a b c
là h ng s ) .ằ ố
b)
( )
2
1 1
21 1
2
1 1 1 1
. 2 . b c
a a x a b x a b
ax bx c
a x b a x b
+ +
� �
+ + =
� �
� �
++
� �
; (
1 1
, , , ,a b c a b
là h ng s ) .ằ ố
Ví d 7.ụTìm đo hàm c a các hàm s sau : ạ ủ ố
a)
= + +
2 4
( 1)y x x
; b)
+
=−
2
3
( 1)
( 1)
x
y
x
; c)
=− +
2 2
1
( 2 5)
y
x x
.
Ví d 8.ụTìm đo hàm c a các hàm s sau : ạ ủ ố
a)
= − +
2
2 5 2y x x
; b)
= − +
2
( 2) 3y x x
; c)
( )
= + − 3
1 1 2y x
.
Ví d 9.ụTìm đo hàm c a các hàm s sau : ạ ủ ố
a)
2 sin 3 cos 5y x x=
; b)
sin cos
sin cos
x x
yx x
+
=−
; c)
2
1 tan 3
2
1 tan 3
x
y
x
+
=−
.
Chú ý : Khi g p các hàm s ph c t p n u có th ta hãy rút g n hàm s r i ặ ố ứ ạ ế ể ọ ố ồ
hãy đi tính đo hàm , đc bi t là đi v i các hàm s có ch a các hàm s ạ ặ ệ ố ớ ố ứ ố
l ng giác.ượ
Ví d 10.ụTìm đo hàm c a các hàm s sau : ạ ủ ố
a)
2
(sin cos )y x x= +
; b)
tan coty x x= +
;
c)
= + +
3 5
2 1
tan2 tan 2 tan 2
3 5
y x x x
; d)
( )
2 3
tan sin cos 2y x
� �
=� �
.
Ví d 11.ụCho hàm s : ố
( )
3 2
12 5
3
y f x x x mx= = − + +
. Tìm
m
đ : ể
a)
( )
0f x x
∀ ﾡ
; b)
( ) ( )
0 , 0;f x x
> ∀ +� �
;
c)
( ) ( )
0 , 0;2f x x
< ∀
; d)
( ) ( )
0 , ; 2f x x
∀ −� � �
.
Ví d 12.ụCho hàm s : ố
( ) ( )
3 2 4 5 1
3 2
m m
f x x x m x m= − + − + +
. Tìm
m
đ : ể
a)
( )
0 ,f x x
< ∀ ﾡ
; b)
( )
0f x
=
có hai nghi m cùng d u.ệ ấ
Bài 6.Tìm đo hàm c a các hàm s sau : ạ ủ ố
a)
5 4 3 2
1 2 3 4 5
2 3 2
y x x x x x= + − − + −
; b)
2 4
1 1 0,5
4 3
y x x x= − + −
;
c)
4 3 2
4 3 2
x x x
y x= − + −
; d)
5 3
4 2 3y x x x x= − + −
;
e)
23
22
x b a
y c x b
ax
= + + + −
(
, ,abc
là h ng s ) . ằ ố
Bài 7.Tìm đo hàm c a các hàm s sau : ạ ủ ố
a)
5
(2 3)( 2 )y x x x= − −
; b)
(2 1)(3 2)y x x x= − +
; c)
( )
1
1 1y x x
� �
= + −
� �
� �
;
d)
2 1
1
x
y
x
−
=−
; e)
3
2 5
yx
=−
; f)
2
1
1
x x
y
x
+ −
=−
;
g)
2
2 4 5
2 1
x x
yx
− +
=+
; h)
2
11
y x x
= + − +
; i)
2
5 3
1
x
yx x
−
=+ +
; k)
2
2
1
1
x x
yx x
+ +
=− +
.
Bài 8.Tìm đo hàm c a các hàm s sau : ạ ủ ố
a)
3 2 2
(2 3 6 1)y x x x= − − +
; b)
2 5
1
( 1)
yx x
=− +
c)
2 3 2 2
( 1) ( 1)y x x x x= − + + +
; d)
2
1
y x x
� �
= −
� �
� �
;