BÀI TẬP VÍ DỤ CŨNG CỐ KIẾN THỨC
CHƯƠNG ĐẠO HÀM VÀ VI TÍCH PHÂN
*Các bạn theo dõi phân tóm tắt lý thuyết để nắm lý thuyết trọng tâm nhé
Dạng bài ôm sát đề thi
Chương: Đạo hàm
*Quy tắc Lopitan
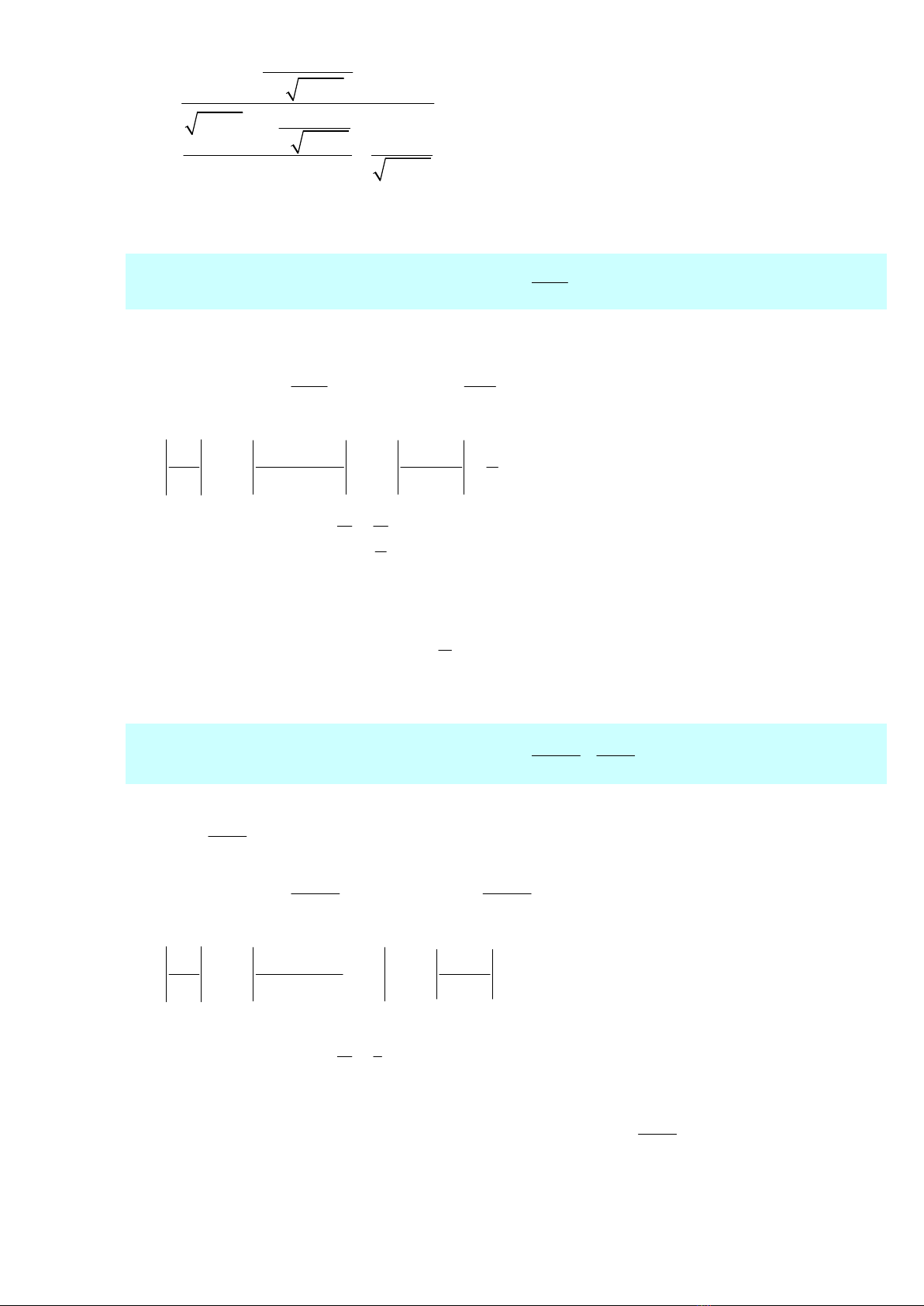
Bài 1: Tính
2
x 0
ln(1 x) x
lim tan x
2 2
x 0 x 0 x 0
2
3 3 2 3
x 0 x 0 x 0
x
ln(1 x) x [ln(1 x) x]' 1 x
lim lim lim 1
tan x (tan x)' 2 tan x cos x
x cos x ( x cos x)' 3cos x.sin x cos x
lim lim lim
2(1 x)sin x (2(1 x)sin x) ' 2sin x 2cos x.(1 x)
1
2
Bài 2: Tính
x4
ln(tan x)
lim cot 2x
2
x x x
4 4 4 2
2 3
x4
1 1
.
ln(tan x) [ln(tan x)]' tan x cos x
lim lim lim 1 1
cot 2x (cot 2x) ' .
sin 2x 2
sin x
lim 1
2sin 2x.cos x
Bài 3: Tính
x 0
1 1
lim x arcsin x
Ta tìm (arcsin x)’.
arcsin x là hàm ngược của sinx nên theo lý thuyết ta tìm đạo hàm của nó như
x ( , )
2 2
sau
Đặt y = sin x
2 2
2
y sin x y' cos x 1 sin x 1 y
1 1
arcsin(sin x)' arcsin y ' y' 1 y
Hay
2
1
arcsin x '
1 x
x 0 x 0 x 0
1 1 arcsin x x (arcsin x x)'
lim lim lim
x arcsin x x.arcsin x (x.arcsin x)'
2
2
x 0 x 0
22
1
11 '
11 x
1 x
lim lim
xx
arcsin x arcsin x '
1 x 1 x
3
2
x 0 2
2
22
2x
2 1 x
lim 0
2x
1 x x. 1
2 1 x
1 x 1 x
*Chuỗi lũy thừa
Bài 4: Tìm miền hội tụ và bán kính hội tụ của
2n
n
n 1
x
n.9
Đặt
2
t x
Chuỗi trở thành với
n
n
n 1
1(t 0)
n.9
nn
1
c9 n
n
n 1
n
n n n
n
c 9 n n 1
lim lim lim 0
c 9.9 .(n 1) 9(n 1) 9
Vậy bán kính hội tụ
1 1
R 9
1
L
9
Xét sự hội tụ tại hai đầu mút
x a 3 3
Tại chuỗi trở thành là chuỗi điều hòa nên phân kỳ.
x a 3 3
n 1
1
n
Vậy miền hội tụ là (-3,3)
Bài 5: Tìm miền hội tụ và bán kính hội tụ của
n
n
n 1
( 1) 1 x
.
2n 1 1 x
Đặt
1 x
t1 x
Chuỗi trở thành với
nn
n 1
( 1) . t 0
2n 1
n
n
( 1)
c2n 1
n 1
n n n
n
c 2n 1 2n 1
lim lim .( 1) lim 1 0
c 2(n 1) 1 2n 3
Vậy bán kính hội tụ
1 1
R 1
L 1
Miền hội tụ của chuỗi là
1 x
a 1 t a 1 1 t 1 1 1 x 0
1 x
Xét sự hội tụ của chuỗi tại đầu mút x = 0
Chuỗi trở thành là chuỗi Lebnizt hội tụ do là chuỗi đan dấu và dãy
n
n 1
( 1)
2n 1
n
n 1
( 1)
2n 1
là dãy dương giảm
n
1
a2n 1
Vậy miền hội tụ là
[0, )
Bài 6: Tìm miền hội tụ và bán kính hội tụ của
1 2n n
n 1
n 1
4. x 3
4
Chuỗi là chuỗi lũy thừa với
1 2n
nn 1
4
c , a 3
4
2n 2 n
n 1
2n n 1
n n
n
c 4 4
lim lim . 4
c 4 4
Vậy bán kính hội tụ
1 1
RL 4
Ta xét sự hội tụ tại 2 đầu mút
1
x a R 3 4
Tại , chuỗi trở thành không hội tụ do với n lẻ, chuỗi hội tụ về -1, với n
1
x 3 4
n
n 1
( 1)
chẵn, chuỗi hội tụ về 0. Điểm hội tụ không có định nên chuỗi không hội tụ.
Tại , chuỗi trở thành là chuỗi phân kỳ
1
x 3 4
n 1
1
Vậy miền hội tụ là
1 1
( 3 , 3 )
4 4
Chương: TÍCH PHÂN
Bài 7: Tính tích phân suy rộng sau
3
3
1dx
x 2
Đây là tích phân suy rộng loại 1.
t
t
3 3
3 3
t t
3
t
t
t
1 1 2
dx lim dx lim x 2
x 2 x 2
2 2
lim t 2 3 2
2 2
khi t 0 lim 0
t 2 t 2
2 2
lim 2
t 2 3 2
Vậy tích phân hội tụ về 2
Bài 8: Tính tích phân suy rộng sau
2 2
0
x.arctanx dx
(1 x )
Dễ thấy đây là tích phân suy rộng loại 1
t
2 2 2 2
0 0
t
x.arctanx x.arctanx
dx lim dx
(1 x ) (1 x )
Ta tìm (arctan x)’, đặt
2 2
y tan x y ' 1 tan x 1 y
Theo cách tìm đạo hàm hàm ngược (arctan x là hàm ngược của tanx )
x ( , )
2 2
2
1 1
arctan(tan x) ' arctan(y) ' y ' 1 y
Hay .
2
1
arctan(x) ' 1 x
Đặt và
2
dx
u arctan x du 1 x
x tan u
Tích phân trở thành
arctan t
arctan t
2
arctan 0
t t
arctan 0
u.tan u 1
lim du lim sin(2x) 2x cos(2x)
1 tan u 8
t
1
lim sin(2arctan t) 2.arctan t.cos(2arctan t) sin 0 2.0.cos 0
8
t
Do khi t arctan t 2
1
lim sin(2arctan t) 2.arctan t.cos(2arctan t) sin 0 2.0.cos0
8 8
Vậy tích phân hội tụ về
8
Bài 9: Tính tích phân suy rộng sau
14
4
2
dx
x 2
Ta thấy đây là tích phân suy rộng loại 2
14 14
4 4
2 t
t 2
dx dx
lim
x 2 x 2
14
3 3 3
4 4 4
t 2 t 2
t
4 4 32
lim x 2 lim 14 2 t 2
3 3 3
Bài 10: Xác định tích phân suy rộng sau hội tụ hay phân kỳ
5
0
xdx
x 2
Ta thấy hàm số không xác định tại x=2
x
f (x) x 2
Vậy đây là tích phân suy rộng loại 2
5 2 5 t 5
0 0 2 0 t
t 2 t 2
t 5
0 t
t 2 t 2
t 2 t 2
xdx xdx xdx xdx xdx
lim lim
x 2 x 2 x 2 x 2 x 2
lim x 2ln (x 2) lim x 2 ln(x 2)
lim t 2ln t 2 2ln 2 lim 5 2ln 3 t 2ln t 2
Ta có *xem thêm đồ thị hàm số y = lnx
t 2
t 2
lim t 2
t 2
khi t 2 0
t 2 lim t 2
Vậy tích phân suy rộng phân kỳ
Bài 11: Tính tích phân suy rộng sau
1
x
0
2
edx
x
Ta thấy tích phân vừa có cận từ vừa có cận tại 0 mà tại đó hàm số không xác
1
x
2
e
f (x) x
định, vậy đây là sự kết hợp của tích phân loại 1 và tích phân loại 2
Tích phân trở thành
1 1 k
1
x x
0 k x
2 2
t
t k 0 t k 0
t
11
tk
t k 0
e e
dx lim lim dx lim lim e
x x
lim lim e e
Khi
1
0
t
1
t 0 e e 1
t
Khi *xem thêm đồ thị
1
k
1
k 0 e e 0
k
x
y e
Vậy tích phân hội tụ về 1
