CAÂU HOÛI TRAÉC NGHIEÄM OÂN CHÖÔNG I
Câu 1: Cho ngũ giác ABCDE. Số các vecto (Khác vecto-không) có điểm đầu và điểm cuối là các đỉnh của
ngũ giác bằng:
a) 20
b) 25
c) 16
d) 10
Câu 2: Cho hình bình hành ABCD tâm O. Khi đó:
a)
BC AD
b)
AB CD

c)
OB OD

d)
AO CO
Câu 3: Cho tam giác đều ABC, cạnh a. Mệnh đề nào sau đây đúng:
a)
AB a
b)
AC a
c)
AC BC
d)
AB AC

Câu 4: Cho hình bình hành ABCD,với giao điểm hai đường chéo là I. Khi đó:
a)
0
AB CD
b)
AB AD BD

c)
AB IA BI
d)
0
AB BD

Câu 5: Cho hình bình hành ABCD. Khi đó,
AB AC AD
a) 2
AC
b)
AC
c)
0
d) 2
3
AC
Câu 6: Cho 4 điểm bất kỳ A, B, C, O. Đẳng thức nào sau đây là đúng:
a)
OA CA CO
b)
AB AC BC

c)
AB OB OA

d)
OA OB BA
Câu 7: Cho tam giác đều ABC, cạnh a. Gọi G là trọng tâm. Khi đó:
AB GC
a)
2 3
3
a
b)
3
a
c)
2
3
a
d)
3
3
a
Câu 8: Cho tam giác ABC, có trung tuyến AM và trọng tâm G. Khẳng định nào sau đây là đúng
a) 1
( )
3
MG MA MB MC
b) 2
( )
3
AG AB AC
c) 3
AM MG
d)
AM AB AC
Câu 9: (1) Điều kiện cần và đủ để C là trung điểm của đoạn AB là 2
BA AC
(2) Điều kiện cần và đủ để C là trung điểm của đoạn AB là
CB CA
(3) Điều kiện cần và đủ để M là trung điểm của đoạn PQ là 2
PQ PM

Trong các câu trên, thì:
a) Câu (1) và câu (3) là đúng.
b) Câu (1) là sai
c) Chỉ có câu (3) sai
d) Không có câu nào sai.
Câu 10: Cho tam giác ABC. Gọi M là điểm trên cạnh AB sao cho MB=3MA. Khi đó, biễu diễn
AM
theo
AB
và
AC
là:
a) 10
4
AM AB AC
b) 13
4
AM AB AC
 
c) 1 1
2 6
AM AB AC

d) 1 1
4 6
AM AB AC

Caâu 11: Töù giaùc ABCD laø hình bình haønh khi vaø chæ khi:
a)
AB DC

b)
AC BD
c)
AB CD

d)
AD CB
Caâu 12: Goïi O laø taâm hình bình haønh ABCD. Vectô naøo sau baèng
OD
:
a)
BO
b)
OC
c)
OB
d)
OA
Caâu 13: Cho
AB
vaø
AC
ngöôïc höôùng vaø {
AB
{ >{
AC
{
a) A naèm giöõa B vaø C b) A laø trung ñieåm cuûa BC
c) B naèm giöõa A vaø C d) C naèm giöõa B vaø A
Caâu 14 : Cho
x
=
AB
vaø
y
=
BC
. Vectô
x
+
y
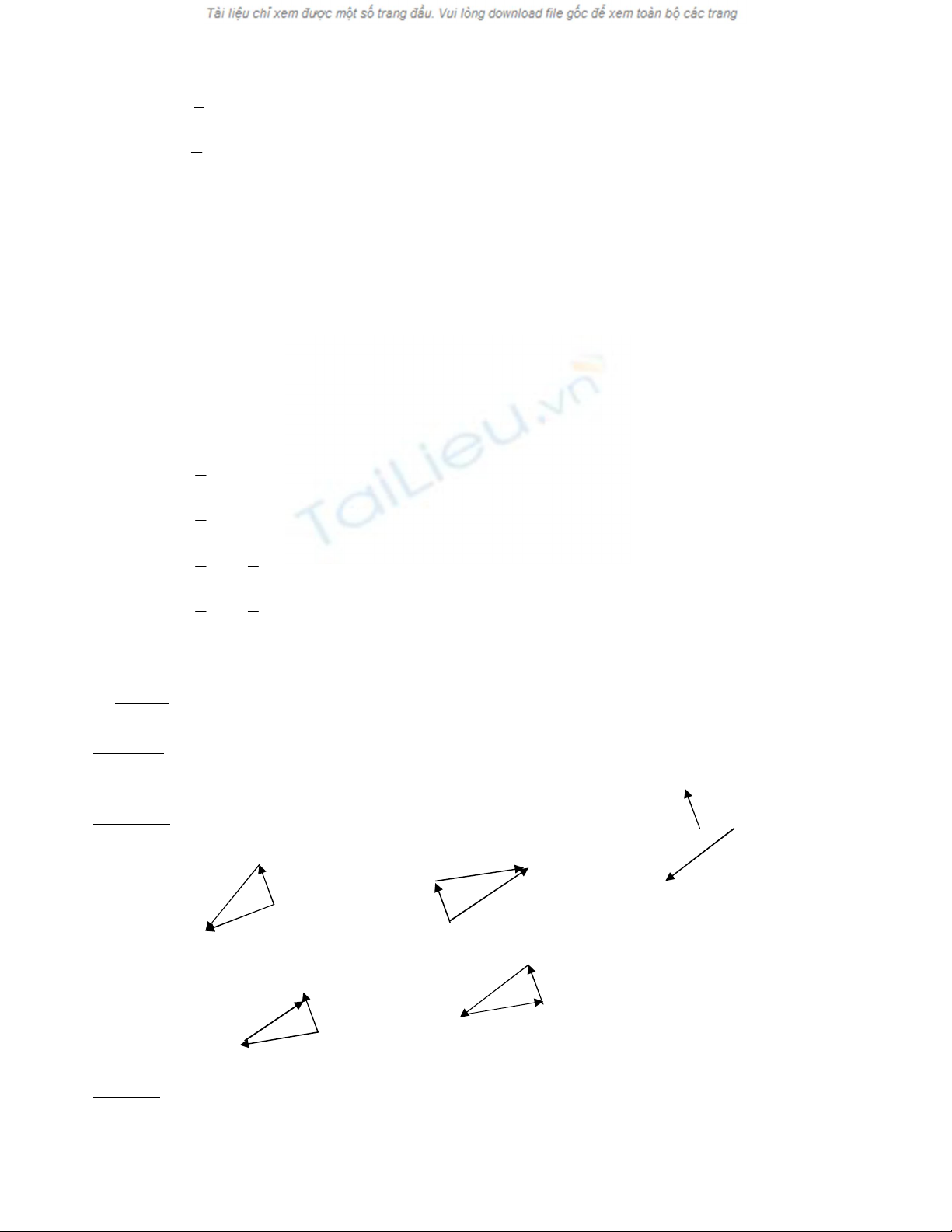
ñöôïc veõ ñuùng hình naøo sau ñaây:
x
a)
x
b)
x
+
y
y
y
x
y
x
+
y
c) d)
y
x
y
x
x
+
y
x
+
y
Caâu 15: Cho hình bình haønh ABCD taâm O. Khi ñoù
OA OB
=
a)
CD
b)
AB
c)
OC OD
d)
OC OB
Caâu 16: Cho tam giaùc ABC ñeàu caïnh a. Khi ñoù {
AB
+
AC
{=
a) a
3
b) a c) 2a d)
3
2
a
Caâu 17: Cho ba ñieåm A,B,C phaân bieät. Ñieàu kieän caàn vaø ñuû ñeå ba ñieåm ñoù thaúng
haøng laø:
a) :
k R AB k AC
b) :
M MA MC MB
c)
AC AB BC

d)
: 0
M MA MB MC

Caâu 18: Cho tam giaùc ABC vôùi trung tuyeán AM vaø troïng taâm G .Khi ñoù
GA
=
a) 2
3
AM

b) 2
GM
c) 1
2
AM

d) 2
3
GM
Caâu 19: Ñieàu kieän naøo sau ñaây khoâng phaûi laø ñieàu kieän caàn vaø ñuû ñeå G laø troïng taâm
cuûa tam giaùc ABC, M laø trung ñieåm cuûa BC.
a)
0
AG GB GC
b)
GA
= 2
3
MA

c)
GM
= -
1
2
GA
d)
0
GA GB GC
Caâu 20: Treân ñöôøng thaúng BC laáy ñieåm M sao cho 3
MB MC
. Ñieåm M ñöôïc veõ
ñuùng ôû hình naøo:
a) B C M b) B M C
c) M C B d) M B C
Câu 21. Cho tứ giác ABCD. Số các vectơ khác
0
có điểm đầu và điểm cuối là đỉnh của tứ giác bằng:
A. 4
B. 6
C. 8
D. 12
Câu 22. Cho lục giác đều ABCDEF có tâm O. Số các vectơ khác
0
cùng phương với
OC
có điểm đầu và
điểm cuối là đỉnh của lục giác bằng:
A. 4
B. 6
C. 7
D. 8
Câu 23. Cho lục giác đều ABCDEF có tâm O. Số các vectơ bằng
OC
có điểm đầu và điểm cuối là đỉnh của
lục giác bằng:
A. 2
B. 3
C. 4
D. 6
Câu 24. Cho hình chữ nhật ABCD có AB = 3, BC = 4. Độ dài của
AC
là:
A. 5
B. 6
C. 7
D. 9
Câu 25. Cho ba điểm phân biệt A, B, C. Đẳng thức nào sau đây là đúng ?
A.
CA BA BC
B.
AB AC BC
C.
AB CA CB

D.
AB BC CA
Câu 26. Cho hai điểm phân biệt A và B. Điều kiện để điểm I là trung điểm của đoạn thẳng AB là:
A.
IA IB
B.
IA IB
C.
IA IB
D.
AI BI
Câu 27. Cho tam giác ABC có G là trọng tâm, I là trung điểm của đoạn thẳng BC. Đẳng thức nào sau đây là
đúng ?
A.
2
GA GI
B.
1
3
IG IA
C.
2
GB GC GI
D.
GB GC GA
Câu 28. Cho hình bình hành ABCD. Đẳng thức nào sau đây là đúng ?
A. 2
AC BD BC

B.
AC BC AB

C. 2
AC BD CD
D.
AC AD CD
Câu 29. Trong mặt phẳng tọa độ Oxy, cho hình bình hành OABC. Gọi C là điểm nằm trên Ox. Khẳng định
nào sau đây là đúng ?
A.
AB
có tung độ khác 0
B. A và B có tung độ khác nhau.
C. C có hoành độ bằng 0
D. A C B
x +x -x = 0
Câu 30. Cho
(3; 2), (1;6)
u v
. Khẳng định nào sau đây là đúng ?
A.
u v
và
( 4;4)
a
ngược hướng.
B.
u
và
v
cùng phương
C.
u v
và
(6; 24)
b
cùng hướng.
D. 2
u v
và
v
cùng phương.
Câu 31. Cho tam giác ABC có A(3; 5), B(1; 2), C(5; 2). Trọng tâm của tam giác ABC là:
A. G1(-3; 4)
B. G2(4; 0)
C. G3(
2
; 3)
D. G4(3; 3)
Câu 32. Cho bốn điểm A(1; 1), B(2; -1), C(4; 3), D(3; 5). Chọn mệnh đề đúng.
A. Tứ giác ABCD là hình bình hành.
B. Điểm
5
2;
3
G
là trọng tâm của tam giác BCD.
C.
AB CD
D. ,
AC AD
cùng phương.
Câu 33. Trong mặt phẳng Oxy cho 4 điểm A(-5; -2), B(-5; 3), C(3; 3), D(3; -2). Khẳng định nào sau đây là
đúng ?
A. ,
AB CD
cùng hướng.
B. Tứ giác ABCD là hình chữ nhật
C. Điểm I(-1; 1) là trung điểm của AC
D.
OA OB OC

Câu 34. Cho tam giác ABC. Đặt ,
a BC b AC

. Các cặp vectơ nào sau đây cùng phương ?
A. 2
a b
và
2
a b
B.
2
a b
và 2
a b
C. 5
a b
và
10 2
a b
D.
a b
và
a b
Câu 35. Trong mặt phẳng tọa độ Oxy, cho hình vuông ABCD có gốc O là tâm của hình vuông và các cạnh
của nó song song với các trục tọa độ. Khẳng định nào sau đây là đúng ?
A.
OA OB AB
B.
OA OB
và
DC
cùng hướng
C.
A C
x x
và
A C
y = y
D.
B C
x x
và
C B
y = - y
Câu 36. Cho M(3; -4). Kẻ MM1 vuông góc với Ox, MM2 vuông góc với Oy. Khẳng định nào sau đây là
đúng ?
A.
3
1
OM
B.
4
2
OM
C.
1 2
OM OM
có tọa độ (-3; -4)
D.
1 2
OM OM

có tọa độ (3; -4).
Câu 37. Trong mặt phẳng tọa độ Oxy, cho A(2; -3), B(4; 7). Tọa độ trung điểm I của đoạn thẳng AB là:
A. (6; 4)
B. (2; 10)
C. (3; 2)
D. (8; -21)
Câu 38. Trong mặt phẳng tọa độ Oxy, cho A(5; 2), B(10; 8). Tọa độ của vectơ
AB
là:
A. (15; 10)
B. (2; 4)
C. (5; 6)
D. (50; 16)
Câu 39. Cho tam giác ABC có B(9; 7), C(11; -1), M và N lần lượt là trung điểm của AB và AC. Tọa độ của
MN
là:
A. (2; -8)
B. (1; -4)
C. (10; 6)
D. (5; 3)
Câu 40. Trong mặt phẳng tọa độ Oxy, cho 4 điểm A(3; -2), B(7; 1), C(0; 1), D(-8; -5). Khẳng định nào sau
đây là đúng ?
A.
AB
và
CD
đối nhau.
B.
AB
và
CD
cùng phương nhưng ngược hướng.
C.
AB
và
CD
cùng phương và cùng hướng.
D. A, B, C, D thẳng hàng.
Câu 41. Cho 3 điểm A(-1; 5), B(5; 5), C(-1; 11). Khẳng định nào sau đây là đúng ?
A. A, B, C thẳng hàng.