Ch ng 1: KHÁI NI M C B N V M CH ĐI N Ngô Ng cươ Ệ Ơ Ả Ề Ạ Ệ ọ
Th ọ
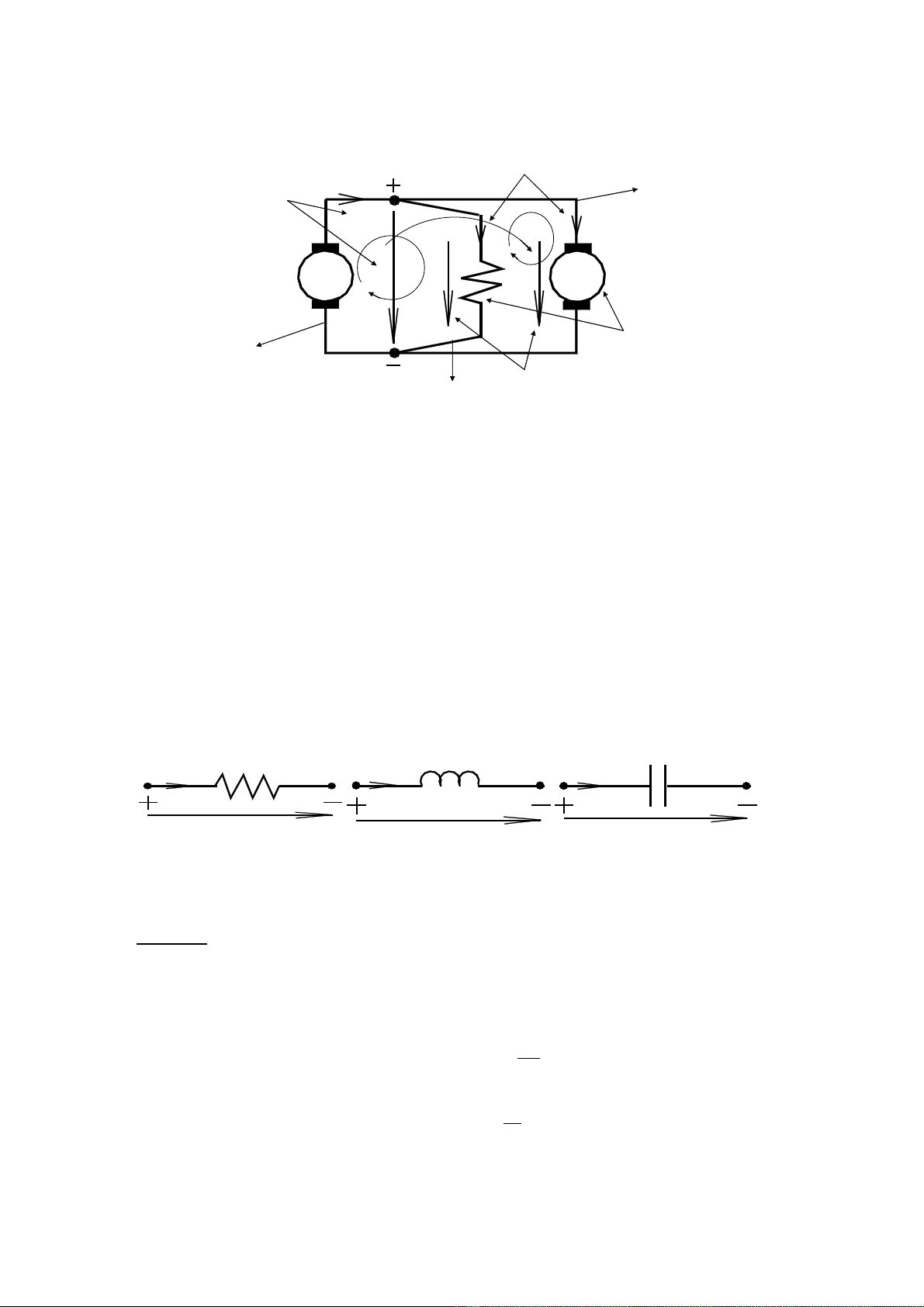
* 3 thành phầncơbảncủa mạchđiệnlà:
Nguồn – Tải– Hệthống đường dẫn
*4thành phầnkếtcấucủa mạchđiện:
- Nhánh (ví dụcác nhánh 1, 2, 3)
- Nút (ví dụcác nút A, B)
- Vòng (ví dụcác vòng a, b, c)
- Mắt(ví dụcác mắta, b)
1.1 Mạchđiện& kếtcấucủamạchđiện
MP ĐC
U
I
1
U
1
U
2
I
2
I
3
A
Nguồn
Tải
Dòng & áp
do nguồncấp
Dòng tảitiêu thụ
Áp tảitiêu thụ
R
B
a
b
c
1
2
3
1.2 Các phầntửcơbảncủamạchđiện
1.2.1 Điệntrở
Điện áp trên điện trở: u
R
= R.i (V)
Chú ý: Bên cạnh khái niệm điện trởR, người ta còn
đưa ra khái niệm điện dẫn G = 1/R, tính bằng
SIEMEN (S).
1.2.2 Điệncảm
Điện áp trên điện cảm: u
L
= L. (V)
1.2.3 Điệndung
Điệnáp trên điệndung: u
C
= (V)
(với u
C
(t
o
) = 0)
R (Ω)
u
R
iL (H)
u
L
i
u
C
C (F)
i
dt
di
∫
t
o
t
idt
C
1
1
Ch ng 1: KHÁI NI M C B N V M CH ĐI N Ngô Ng cươ Ệ Ơ Ả Ề Ạ Ệ ọ
Th ọ
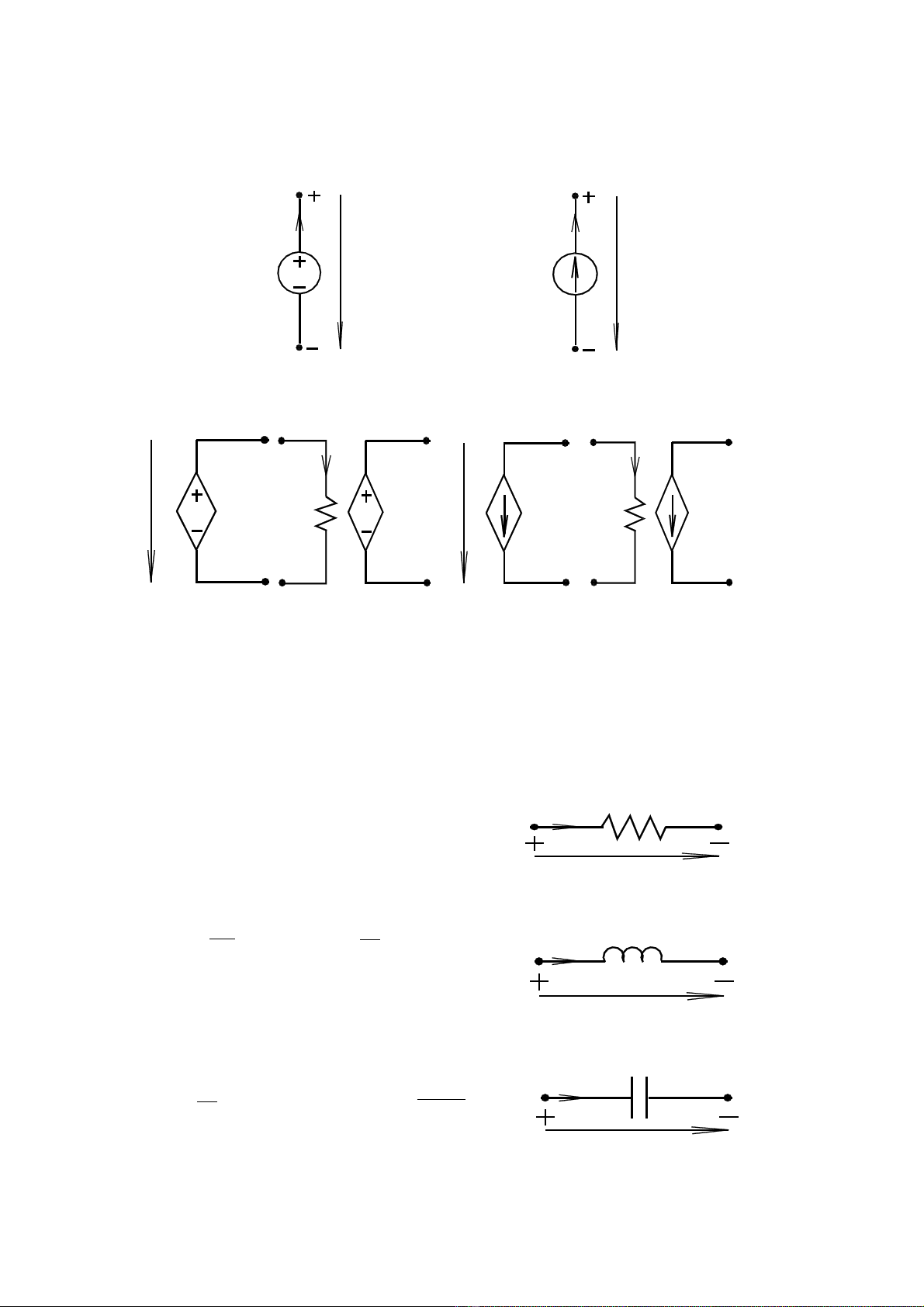
1.2.4 Nguồnđiện
1.2.4.1 Nguồnđộclập
1.2.4.2 Nguồnphụthuộc
u
1
i
u=e=const
e j u
i=j=const
Nguồnáp độclậpNguồndòng độclập
ku
1
i
1
ki
1
i
1
ki
1
u
1
ku
1
Nguồnáp phụ
thuộcáp Nguồnáp phụ
thuộcdòng
Nguồndòng
phụthuộcáp
Nguồndòng
phụthuộcdòng
1.3.1 Định luậtOHM đ/v mộtđoạnmạch
- Đọan mạchthuầnTRỞ
u
R
= R.i (V) ↔i = u
R
/R (A)
- Đọan mạchthuầnCẢM
↔
(với i(t
o
) = 0
- Đọan mạchthuầnDUNG
↔
(với u
C
(t
o
) = 0)
1.3 Định luậtOHM
R (Ω)
u
R
i
L (H)
u
L
i
u
C
C (F)
i
)V(
dt
di
Lu
L
=
)A(dtu
L
1
i
t
t
L
o
∫
=
)A(
dt
du
Ci
C
=
)V(idt
C
1
u
t
t
C
o
∫
=
2
Ch ng 1: KHÁI NI M C B N V M CH ĐI N Ngô Ng cươ Ệ Ơ Ả Ề Ạ Ệ ọ
Th ọ
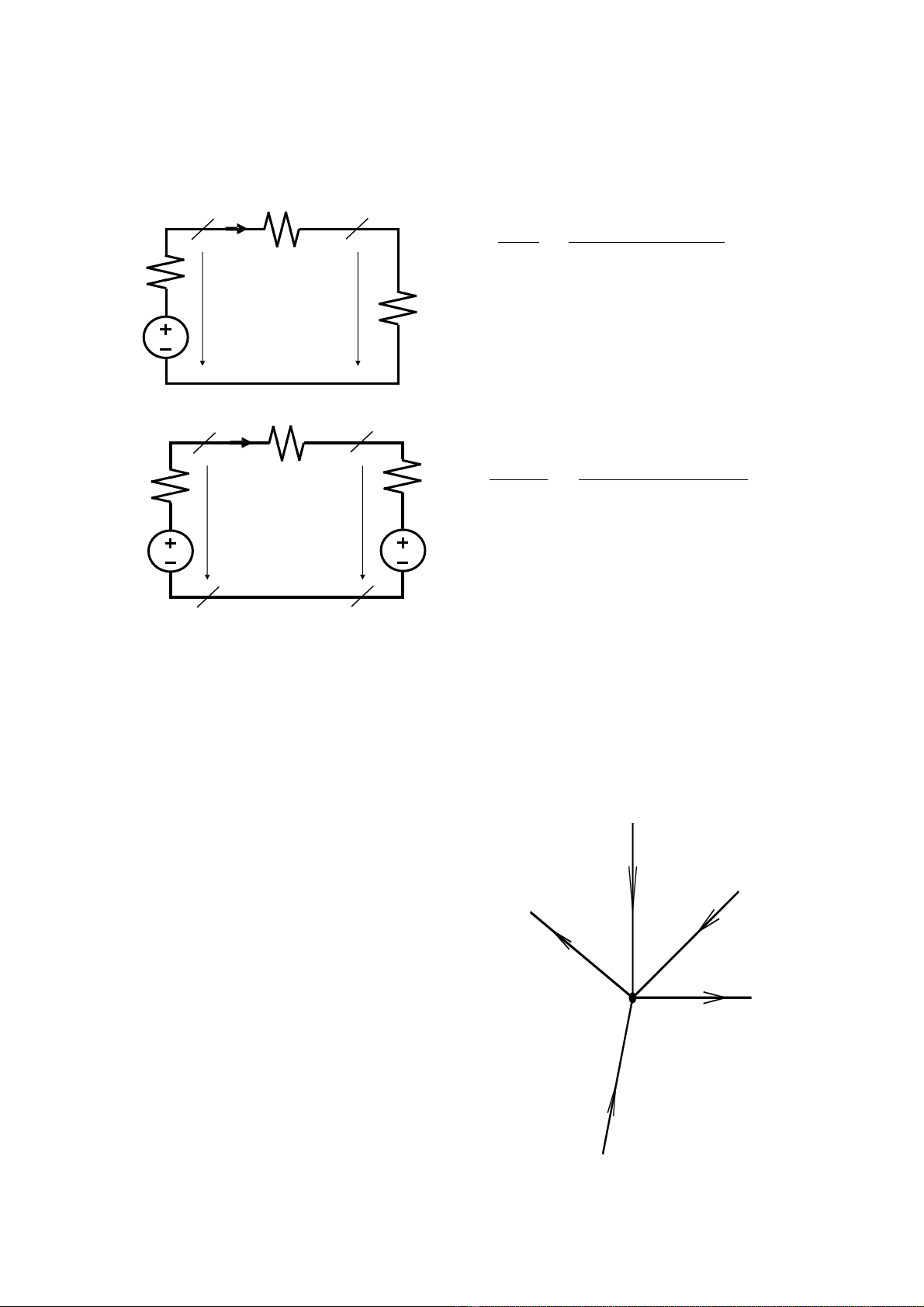
1.3.2 Định luậtOHM đ/v toàn mạch
R
o
’
tdo
RRR
e
R
e
i++
==
∑
o
R.ieu −=
tt
R.iu =
'R.i'e'u
o
+=
'RRR
'ee
R
'ee
i
odo
++
−
=
−
=
∑
••
e’
e
R
o
R
d
•
R
t
i
uu
t
•
R
d
e
R
o
i
uu’
••
••
1.4. Định luậtKIRCHHOFF
1.4.1 Định luậtKIRCHHOFF 1 (định luậtnút)
Σi (đến một nút) = Σi (rời nút đó)
Ví dụtại nút A: i
1
+ i
2
+ i
4
= i
3
+ i
5
Hay: i
1
+ i
2
– i
3
+ i
4
– i
5
= 0
Vậy, định luật K1, được phát biểu
theo cách thứhai nhưsau:
Σ
đại số
i (tại một nút) = 0,
trong đó, dòng nào hướng đến nút
mang dấu (+), dòng nào rời khỏi
nút mang dấu (-)
A
i
1
i
3
i
2
i
4
i
5
3
Ch ng 1: KHÁI NI M C B N V M CH ĐI N Ngô Ng cươ Ệ Ơ Ả Ề Ạ Ệ ọ
Th ọ
e
2
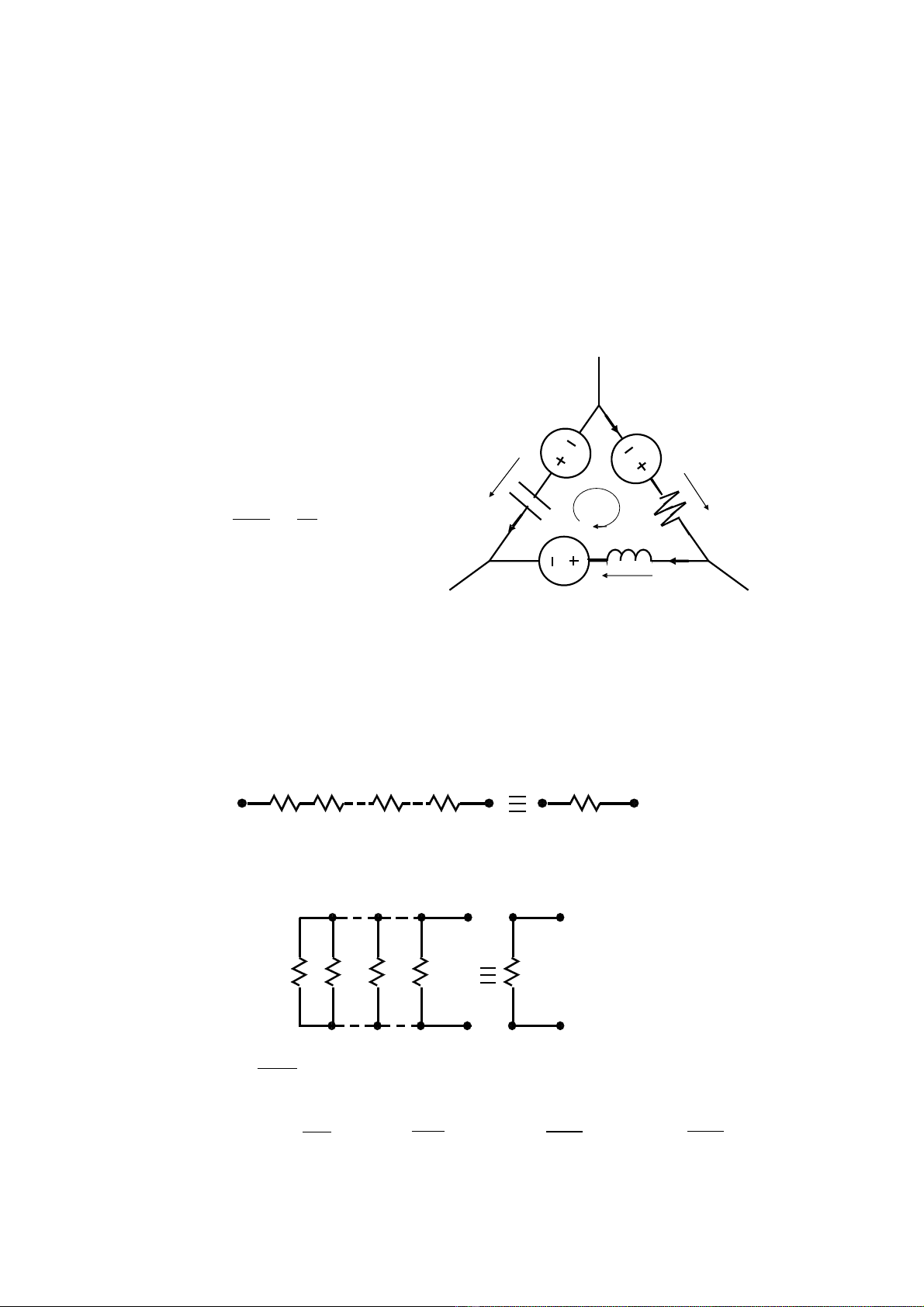
1.4.2 Định luậtKIRCHHOFF 2 (định luậtvòng)
Σ
đạisố
u (trong một vòng kín)
= Σ
đạisố
e (trong vòng kín đó),
trong đó, sức điện động và điện áp nào cùng chiều
với chiều của vòng thì mang dấu (+), ngược với
chiều của vòng thì mang dấu (-)
Ví dụtrong vòng ABCA:
u
R
+ u
L
- u
C
= e
1
- e
2
- e
3
Hay:
u
L
•
••
A
B
i
1
i
3
e
1
e
3
u
R
u
C
i
2
CR
L
C
∫
−+
t
t3
2
1
o
dti
C
1
dt
di
Li.R
321
eee −−=
với u
C
(t
o
) = 0
1.5 Các phép biếnđổitương đương
1.5.1 Phép biếnđổinốitiếp
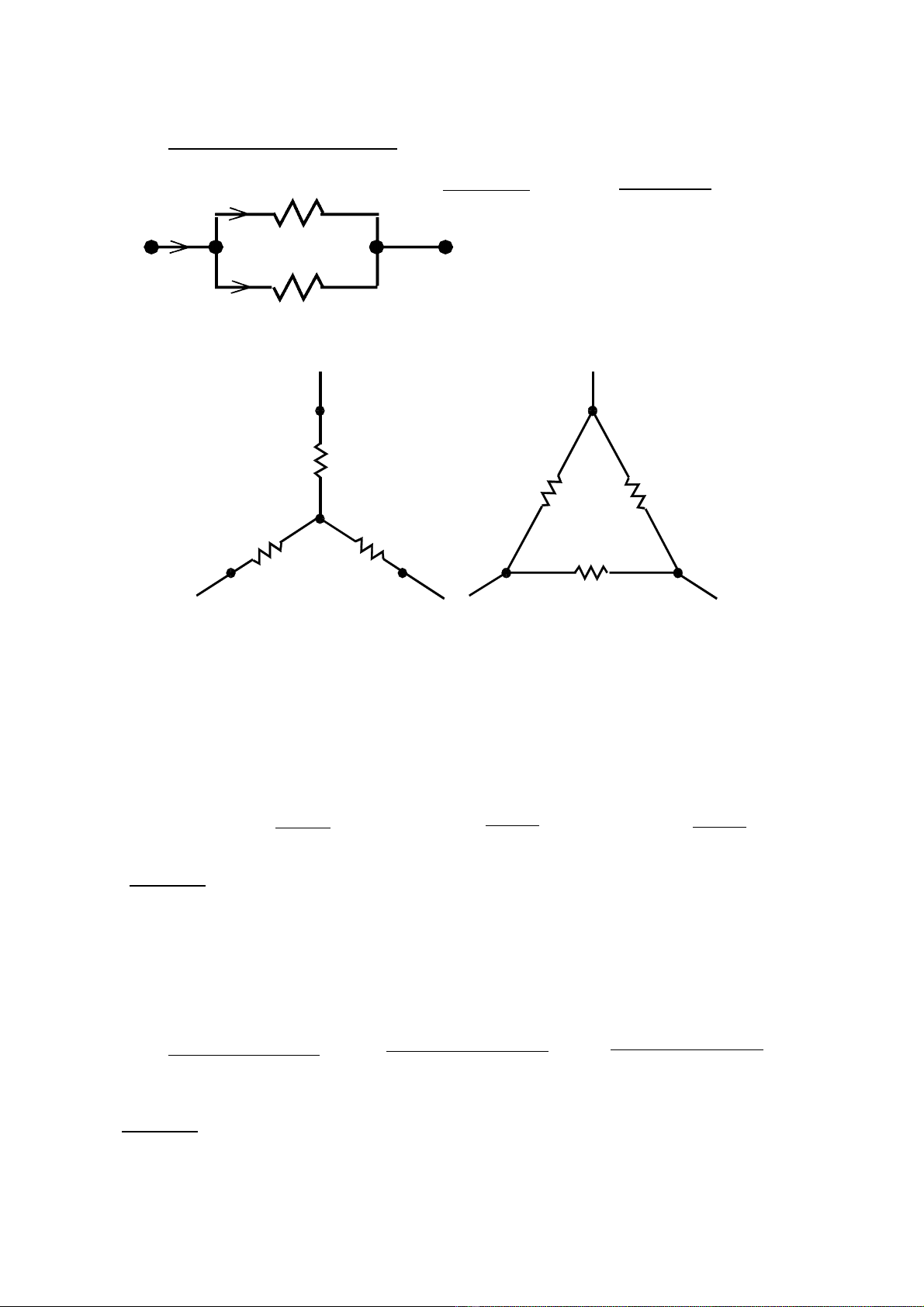
1.5.2 Phép biếnđổisong song
,
R
1
R
2
R
k
R
n
R
TĐ
R
TĐ
=R
1
+R
2
+…+R
K
+…+R
n
TĐ
TĐ
G
R1
=
,
với
nkTĐ
GGGGG +++++= ......
21
trong đó:
,
1
1
1
R
G=
,...,
1
2
2
R
G=
,...,
1
k
k
R
G=
n
n
R
G1
=
R
1
R
2
R
n
R
k
R
TĐ
4
Ch ng 1: KHÁI NI M C B N V M CH ĐI N Ngô Ng cươ Ệ Ơ Ả Ề Ạ Ệ ọ
Th ọ
R
2
I
1
I
2
I
R
1
Trường hợp đặcbiệt:
(Công thức chia dòng)
12
III −=
và:
21
21
.
RR
RR
R
TĐ
+
=
)(
21
2
1
RR
R
II +
=
;
1.5.3 Phép biếnđổiY-∆và ∆-Y
A
BC
R
BC
R
CA
R
AB
R
A
R
B
R
C
A
B
C
O
THĐB:
NếuR
A
= R
B
= R
C
= R
Y
thì R
AB
= R
BC
= R
CA
= R
∆
= 3R
Y
•Phép biến đổiY → ∆
BiếtR
A
,R
B
,R
C
, tìm R
AB
,R
BC
,R
CA
•Phép biến đổi∆ → Y
BiếtR
AB
,R
BC
,R
CA
, tìm R
A
,R
B
,R
C
THĐB:
NếuR
AB
= R
BC
= R
CA
= R
∆
thì R
A
= R
B
= R
C
= R
Y
= R
∆
/3
B
AC
ACC A
R
RR
RRR .
++=
C
BA
BAA B
R
RR
RRR .
++=
A
CB
CBB C
R
RR
RRR .
++=
;;
C AB CA B
C AA B
A
RRR
RR
R++
=.
C AB CA B
A BB C
B
RRR
RR
R++
=.
C AB CA B
B CC A
C
RRR
RR
R++
=.
;
;
5