CÁC CHUYÊN ĐỀ BỒ I DƯ Ỡ NG HSG MÔN TOÁN 7–PHẦ N HÌNH HỌ C
Trầ n Ngọ c Đạ i,THCS Thụ y Thanh 1
CHUYÊN ĐỀ 2
PHƯ Ơ NG PHÁP TAM GIÁC BẰ NG NHAU
A. LÝ THUYẾ T
1. Hai tam giác bằ ng nhau
Hai tam giác bằ ng nhau là hai tam giác có các cạ nh tư ờ ng ứ ng bằ ng nhau, các góc
tư ơ ng ứ ng bằ ng nhau.
ABC = A’B’C’
AB A 'B' ; AC = A'C' ; BC = B'C'
A A ' ; B B' ; C C'
2. Các trư ờ ng hợ p bằ ng nhau củ a tam giác
a) Trư ờ ng hợ p 1 : cạ nh – cạ nh – cạ nh
Nế u ba cạ nh củ a tam giác này bằ ng ba cạ nh củ a tam giác kia thì hai tam giác đó bằ ng
nhau.
b) Trư ờ ng hợ p 2 : cạ nh – góc – cạ nh
Nế u hai cạ nh và góc xen giữ a củ a tam giác này bằ ng hai cạ nh và góc xen giữ a củ a tam
giác kia thì hai tam giác đó bằ ng nhau.
c) Trư ờ ng hợ p 3 : góc – cạ nh – góc
Nế u mộ t cạ nh và hai góc kề củ a tam giác này bằ ng mộ t cạ nh và hai góc kề củ a tam
giác kia thì hai tam giác đó bằ ng nhau.
3. Các trư ờ ng hợ p bằ ng nhau củ a tam giác vuông
a) Trư ờ ng hợ p 1 : hai cạ nh góc vuông (cạ nh – góc - cạ nh)
Nế u hai cạ nh góc vuông củ a tam giác vuông này bằ ng hai cạ nh góc vuông củ a tam giác
vuông kia thì hai tam giác vuông đó bằ ng nhau.
b) Trư ờ ng hợ p 2 : cạ nh huyề n – góc nhọ n (góc – cạ nh – góc)
Nế u cạ nh huyề n và mộ t góc nhọ n củ a tam giác vuông này bằ ng cạ nh huyề n và mộ t góc
nhọ n củ a tam giác vuông kia thì hai tam giác vuông đó bằ ng nhau.
c) Trư ờ ng hợ p 3 : cạ nh huyề n – cạ nh góc vuông (cạ nh – cạ nh – cạ nh)
Nế u cạ nh huyề n và mộ t cạ nh góc vuông củ a tam giác vuông này bằ ng cạ nh huyề n và
mộ t cạ nh góc vuông củ a tam giác vuông kia thì hai tam giác vuông đó bằ ng nhau.
CÁC CHUYÊN ĐỀ BỒ I DƯ Ỡ NG HSG MÔN TOÁN 7–PHẦ N HÌNH HỌ C
Trầ n Ngọ c Đạ i,THCS Thụ y Thanh 2
4. Ứ ng dụ ng
Chúng ta thư ờ ng vậ n dụ ng các trư ờ ng hợ p bằ ng nhau củ a tam giác để :
-Chứ ng minh :hai tam giác bằ ng nhau,hai đoạ n thẳ ng bằ ng nhau,hai góc bằ ng
nhau; hai đư ờ ng thẳ ng vuông góc ; hai đư ờ ng thẳ ng song song;ba điể m thẳ ng hàng ; …
-Tính :các độ dài đoạ n thẳ ng ;tính số đo góc ; tính chu vi ; diệ n tích ; …
-So sánh :các độ dài đoạ n thẳ ng ; so sánh các góc ; …
B. CÁC VÍ DỤ
Ví dụ 1. Cho tam giác ABC. Chứ ng minh rằ ng :
a) Nế u AB = AC thì
B C
;
b) Nế u
B C
thì AB = AC.
Giả i :
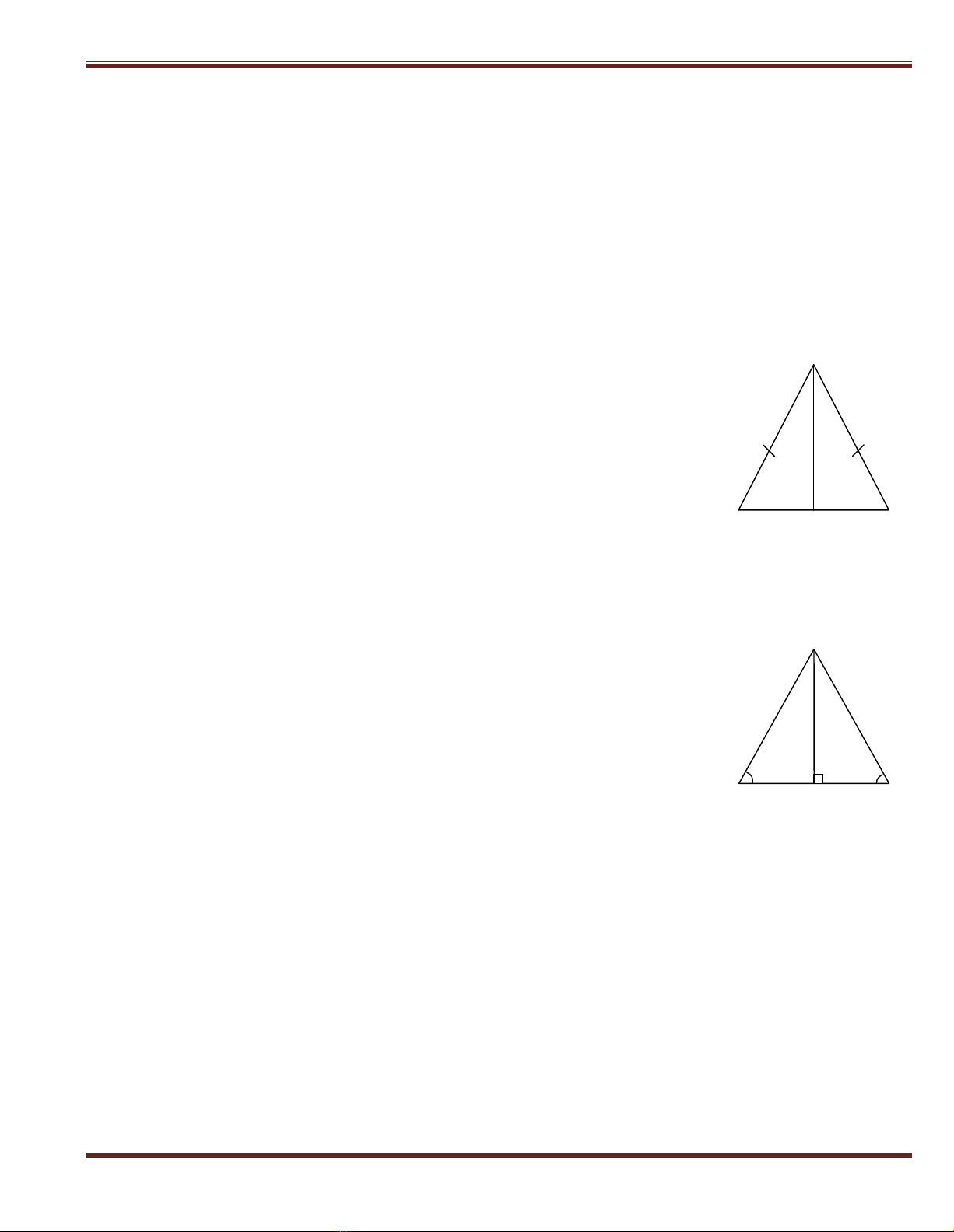
a) (Hình 1)
Cách 1. Gọ i M là trung điể m củ a BC.
Xét AMB và AMC có :
AB = AC (gt) ; BM = CM (cách dự ng) ; AM chung
Do đó :AMB = AMC (c –c–c).
Suy ra :
B C
.
Cách 2. Xét ABC và ACB có :
AB = AC (gt) ; BC chung ; AC = AB (gt)
Do đó :ABC = ACB (c –c–c)
B C
.
b) (Hình 2).Kẻ AH BC (H BC). Tam giác AHB và AHC
cùng vuông tạ i H nên :
0
1
0
2
A B 90
A C 90
, mà
B C
(gt) nên suy ra :
1 2
A A
.
Xét AHB và AHC có :
0
AHB AHC 90
; AH chung ;
1 2
A A
(chứ ng minh trên)
Do đó :AHB = AHC (g –c - g) AB = AC (đpcm).
Ví dụ 2. Cho tam giác ABC có AB = AC. Gọ i M là mộ t điể m nằ m trong tam giác sao
cho MB = MC ; N là trung điể m củ a BC.Chứ ng minh rằ ng :
a) AM là tia phân giác củ a góc BAC ;
b) Ba điể m A, M, N thẳ ng hàng ;
c) MN là đư ờ ng trung trự c củ a đoạ n thẳ ng BC.
C
A
M
Hình 1
C
A
H
Hình 2
1
2
CÁC CHUYÊN ĐỀ BỒ I DƯ Ỡ NG HSG MÔN TOÁN 7–PHẦ N HÌNH HỌ C
Trầ n Ngọ c Đạ i,THCS Thụ y Thanh 3
Giả i :(Hình 3)
a) Xét AMB và AMC có :
AB = AC (gt) ; AM chung ; MB = MC (gt)
Do đó :AMB = AMC (c –c–c)
BAM CAM
.
Vậ y AM là phân giác củ a góc BAC (đpcm).
b) Xét ANB và ANC có :
AB = AC (gt) ; AN chung ; NB = NC (gt)
Do đó :ANB = ANC (c –c–c)
BAN CAN
.
Hay AN là phân giác củ a góc BAC (đpcm).
Vì AM, AN đề u là phân giác củ a góc BAC nên hai tia AM và
AN trùng nhau.
Vậ y ba điể m A, M, N thẳ ng hàng.
c) Theo câu b) thì ANB = ANC (c –c–c)
ANB ANC
.
Mà
0
ANB ANC BNC 180
0
ANB ANC 90
AN BC hay MN BC.
Mặ t khác NB = NC (gt) nên MN là đư ờ ng trung trự c củ a BC.
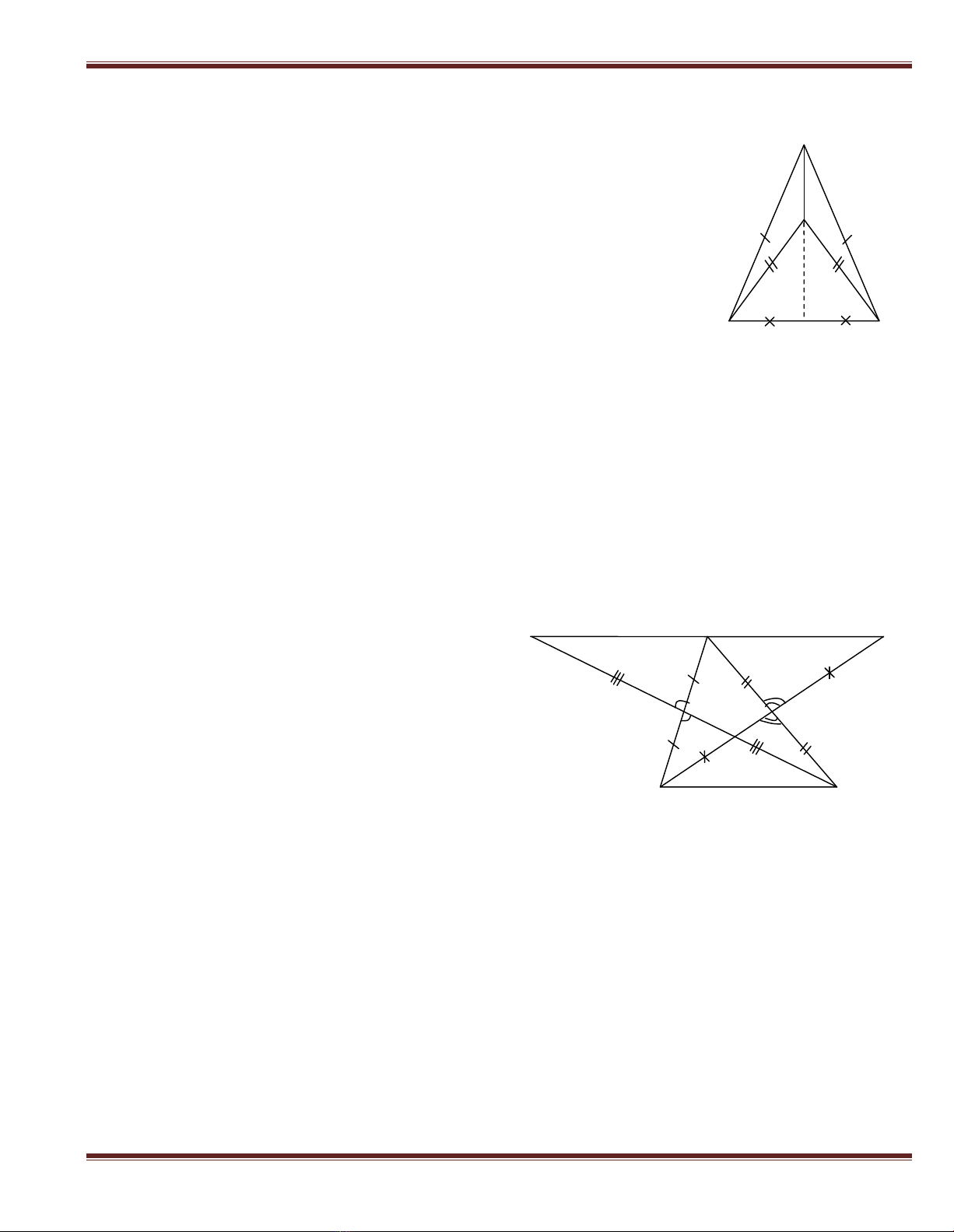
Ví dụ 3. Cho tam giác ABC. Gọ i M, N lầ n lư ợ t là trung điể m củ a AC, AB. Trên tia đố i
củ a tia MB và MC lấ y tư ơ ng ứ ng hai điể m D và E sao cho MB = MD và NC = NE. Chứ ng
minh rằ ng :
a) AD = AE ;
b) Ba điể m A, E, D thẳ ng hàng.
Giả i :(hình 4)
a) Xét MAD và MCB có :
MB = MD (gt)
AMD CMB
(hai góc đố i đỉ nh)
MA = MC (gt)
Do đó MAD = MCB (c –g–c), suy ra AD = BC (1)
Chứ ng minh tư ơ ng tự ta cũng có AE = BC (2)
Từ (1) và (2) suy ra AD = AE.
b) Vì MAD = MCB (chứ ng minh trên) nên
MAD MCB
.
Hai góc này ở vị trí so le trong nên AD // BC.
Chứ ng minh tư ơ ng tự ta cũng có AE // BC.
Qua điể m A có hai đư ờ ng thẳ ng AD và AE cùng song song vớ i BC.Theo tiên đề Ơ cơ lit
thì hai đư ờ ng thẳ ng này trùng nhau.Hay ba điể m A, E, D thẳ ng hàng.
Ví dụ 4. Cho tam giác ABC vuông tạ i B và AC = 2AB. Kẻ phân giác AE (E BC).
a) Chứ ng minh EA = EC ;
b) Tính các góc A và C củ a tam giác ABC.
C
B
N
Hình 3
M
C
B
E
M
Hình 4
CÁC CHUYÊN ĐỀ BỒ I DƯ Ỡ NG HSG MÔN TOÁN 7–PHẦ N HÌNH HỌ C
Trầ n Ngọ c Đạ i,THCS Thụ y Thanh 4
Giả i :(hình 5)
a) Gọ i D là trung điể m củ a AC. Nố i ED.
Vì AC = 2AB (gt) và AC = 2AD (vì D là trung điể m củ a AC) nên AB = AD = CD.
ABC vuông tạ i B nên
0
B 90 .
Xét AEB và AED có :
AE chung
1 2
A A
(vì AE là phân giác củ a góc BAC)
AB = AD (chứ ng minh trên)
Do đó :AEB = AED (c –g–c)
0
ADE B 90
Vì
ADE
và
CDE
là hai góc kề bù nên
0
ADE CDE 90
.
Xét EDA và EDC có :
DE chung
ADE CDE
(chứ ng minh trên)
AD = DC (vì D là trung điể m củ a AC)
Do đó :EDA = EDC (c –g–c) EA = EC.
b) Vì EDA = EDC (chứ ng minh trên) nên
2
A C
. Suy ra
BAC 2C
ABC có :
0
B BAC C 180
hay :
0 0
90 2C C 180
0
C 30
;
0
BAC 2C 60
Vậ y
0 0
A 60 ; C 30
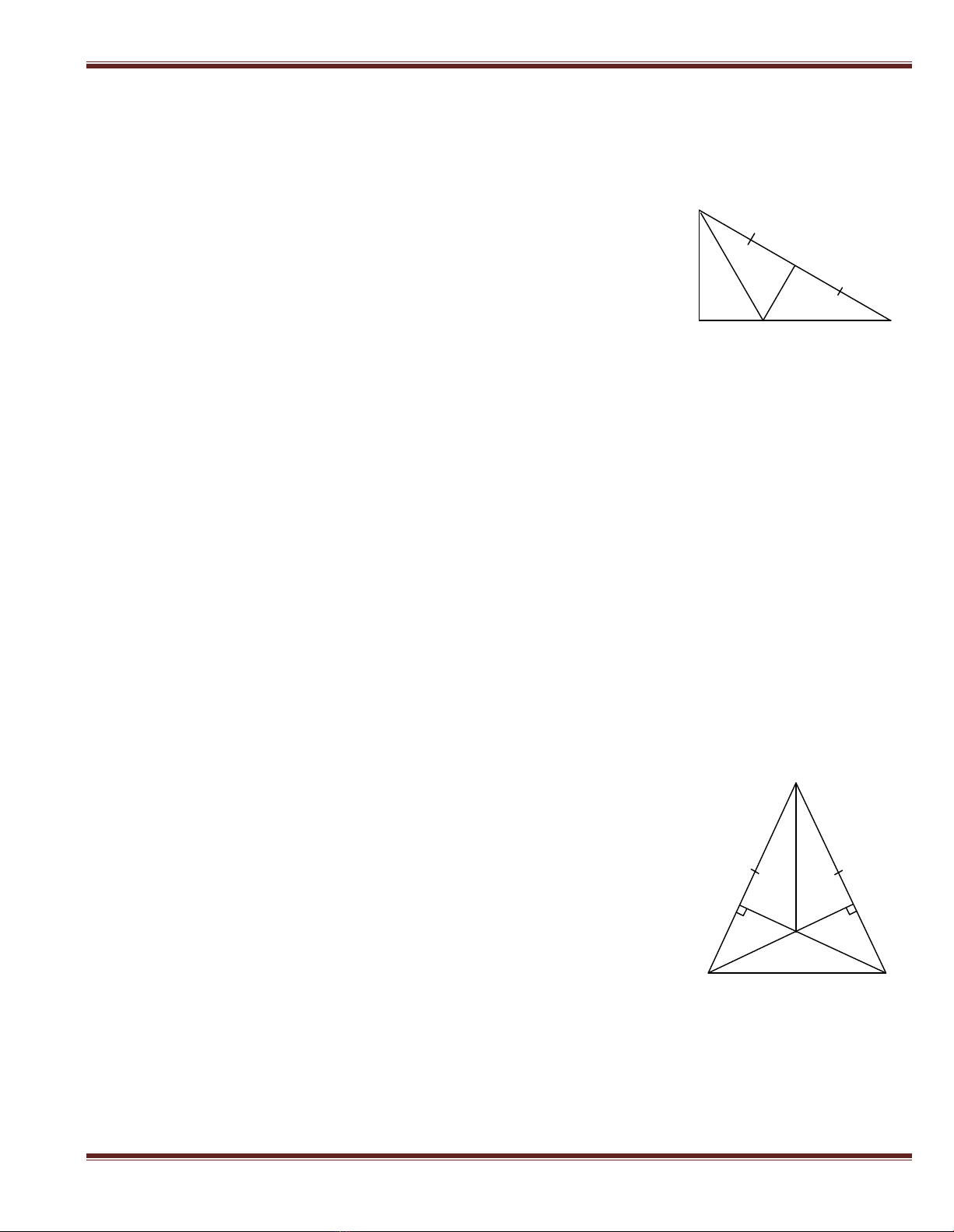
Ví dụ 5. Cho tam giác ABC có
0
A 90
và AB = 2AC. Kẻ BD và CE tư ơ ng ứ ng vuông
góc vớ i AC và AB (D AC, E AB). Gọ i O là giao điể m củ a BD và CE.Chứ ng minh rằ ng:
a) BD = CE ;
b) OE = OD và OB = OC ;
c) AO là tia phân giác củ a góc BAC.
Giả i :
a) Xét ADB và AEC có :
AB = AC (gt) ;
A
chung ;
0
E D 90
Do đó :ADB = AEC (cạ nh huyề n – góc nhọ n)
Suy ra : BD = CE.
b) Vì ADB = AEC (cmt) nên AD = AE.
Xét ADO và AEO có :
AD = AE (gt) ; AO chung ;
0
E D 90
.
Do đó :ADB = AEC (cạ nh huyề n – cạ nh góc vuông).
Suy ra : OD = OE và
OAD OAE
.
C
E
D
Hình 5
1
2
C
A
O
Hình 6
CÁC CHUYÊN ĐỀ BỒ I DƯ Ỡ NG HSG MÔN TOÁN 7–PHẦ N HÌNH HỌ C
Trầ n Ngọ c Đạ i,THCS Thụ y Thanh 5
Lạ i có : BD = CE hay OB + OD = OC + OE OB = OC (vì OD = OE).
Vậ y OD = OE và OB = OC.
c) Theo câu b),
OAD OAE
AO là tia phân giác củ a góc BAC.
BÀI TẬ P
Trư ờ ng hợ p cạ nh – cạ nh -cạ nh
1. Cho ABC = A’B’C’.Gọ i M và M’ tư ơ ng ứ ng là trung điể m củ a BC và B’C’.Bế t
AM = A’M’. Chứ ng minh rằ ng :
a) AMB = A’M’B’ ; b)
AMC A 'M 'C'.
2. Cho ABC. Vẽ cung tròn tâm C bán kính bằ ng AB,cung tròn tâm B bán kính bằ ng
AC. Hai cung tròn trên cắ t nhau tạ i D (A và D thuộ c hai nử a mặ t phẳ ng đố i nhau bờ
BC). Chứ ng minh CD // AB và BD // AC.
3. Cho góc nhọ n xOy. Trên tia Ox, Oy lấ y tư ơ ng ứ ng hai điể m A và B sao cho OA = OB.
Vẽ đư ờ ng tròn tâm A và tâm B có cùng bán kính sao cho chúng cắ t nhau tạ i hai điể m
M, N nằ m trong góc xOy. Chứ ng minh rằ ng :
a) OMA = OMB và ONA = ONB ; b) Ba điể m O, M, N thẳ ng hàng ;
c) AMN = BMN ; d) MN là tia phân giác củ a góc AMB.
4. Cho ABC có AB = AC. Gọ i H là trung điể m củ a cạ nh BC.
a) Chứ ng minh AH vuông góc vớ i BC và là tia phân giác củ a góc BAC ;
b) Trên tia đố i củ a HA lấ y điể m K sao cho HK = HA. Chứ ng minh rằ ng CK // AB.
5. Cho ABC có AB = AC. Gọ i D và E là hai điể m trên BC sao cho BD = DE = EC.
a) Chứ ng minh
EAB DAC
;
b) Gọ i M là trung điể m củ a BC.Chứ ng minh AM là tia phân giác củ a góc DAE ;
c) Giả sử
0
DAE 60 .
Có nhậ n xét gì về các góc củ a AED.
6. Cho ABC. Vẽ đoạ n AD vuông góc vớ i AB (C và D nằ m ở hai nử a mặ t phẳ ng đố i
nhau bờ AC), AE = AC. Biế t rằ ng DE = BC. Tính
BAC.
7. Cho đoạ n thẳ ng AB.Hai điể m C và D nằ m khác phía đố i vớ i AB sao cho C và D cùng
cách đề u hai điể m A và B.
a) Chứ ng minh rằ ng CD là tia phân giác củ a góc ACB ;
b) Kế t quả củ a câu a có đúng không nế u C và D nằ m cùng phía đố i vớ i AB ?
Trư ờ ng hợ p cạ nh – góc - cạ nh
8. Cho góc xOy nhọ n và tia Oz là tia phân giác củ a góc đó.Trên tia Ox lấ y điể m A, trên
tia Oy lấ y điể m B sao cho OA = OB. Gọ i C là mộ t điể m trên tia Oz. Chứ ng minh rằ ng :
a) AC = BC và
xAC yBC
; b) AB vuông góc vớ i Oz.