Toán 7 – H c Kì I – Nguy n Văn Quy n – 0938.59.6698 – s u t m và biên so nọ ễ ề ư ầ ạ
CHUYÊN Đ Ề3 – ĐNG TRÒN. TAM GIÁCƯỜ
A. Lý thuy tế
1. Đng trònườ
1.1. Đng trònườ
-Đng tròn tâm O, bán kính R là hình g m các đi m cách O m t kho ng b ng ườ ồ ể ộ ả ằ
R, kí hi u (O; R)ệ
-
N n m bên trong ằ
P n m bên ngoài ằ
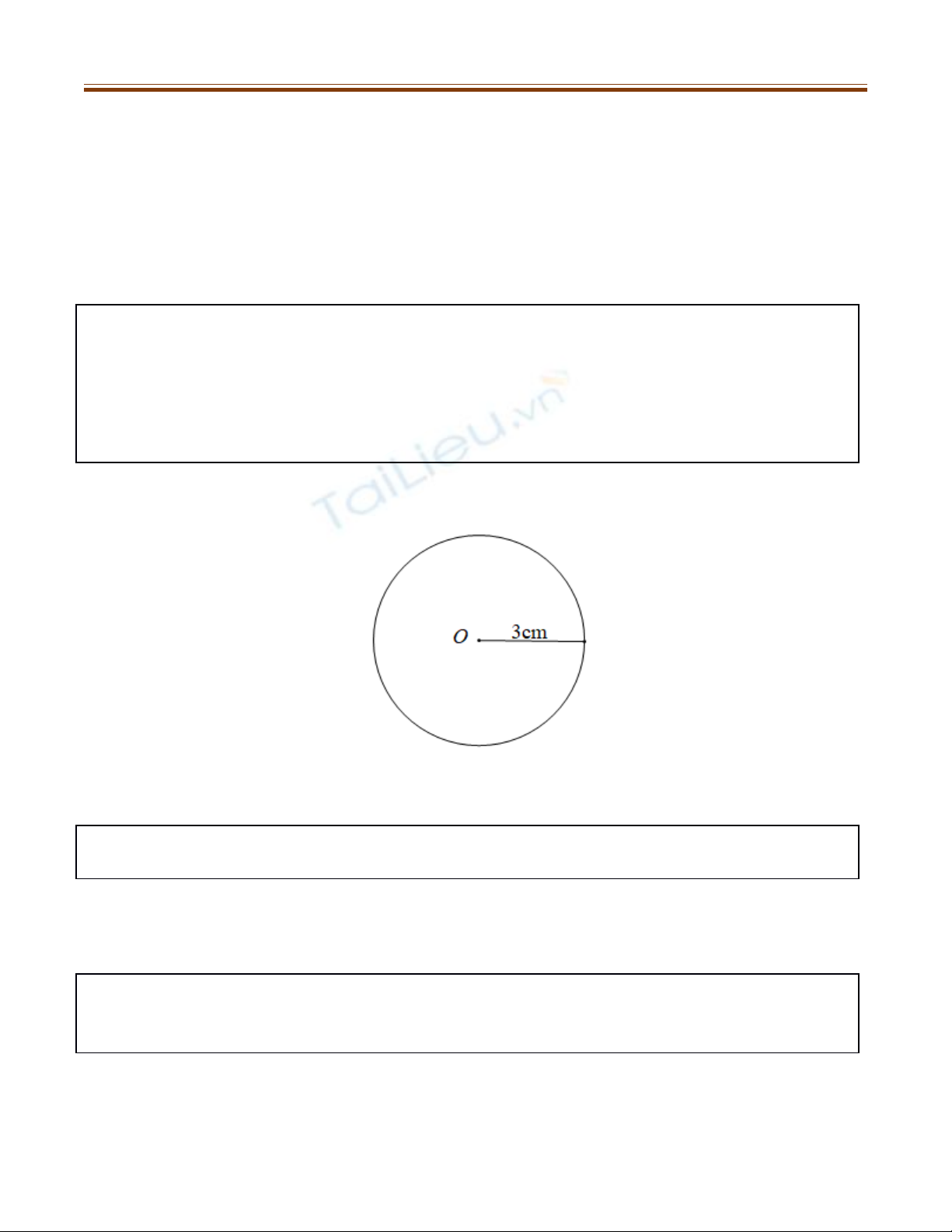
Ví d : Đng tròn (O; 3cm)ụ ườ
1.2. Hình tròn
-Hình tròn là hình g m các đi m n m trên đng tròn và các đi m n m trong ồ ể ằ ườ ể ằ
đng tròn đó. ườ
Ví d : Cái đĩa, đng h , … ụ ồ ồ
1.3. Dây cung
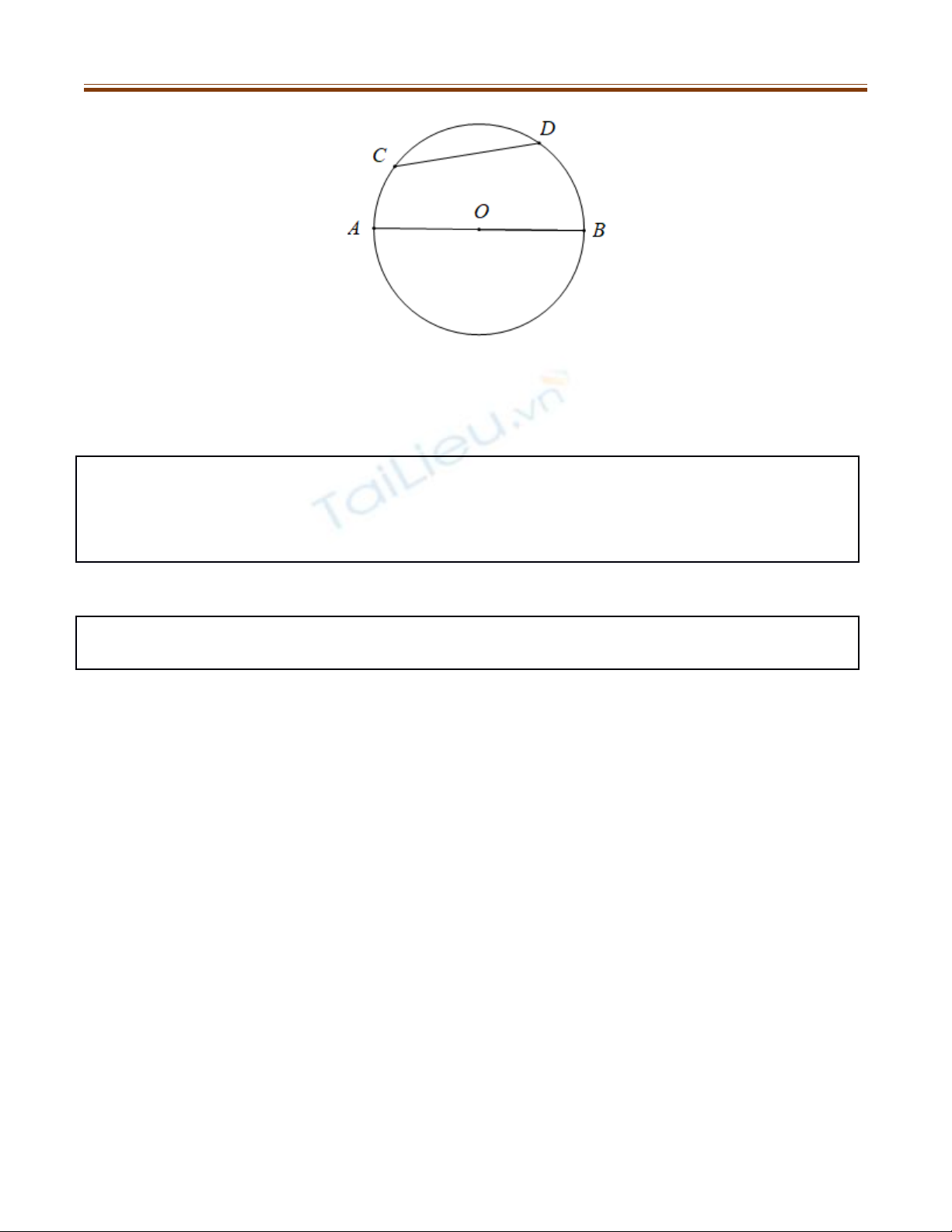
-Hai đi m C, D c a m t đng tròn chia đng tròn thành hai cung. Đo n ể ủ ộ ườ ườ ạ
th ng n i hai mút c a m t cung là dây cung. Dây cung đi qua tâm là đng ẳ ố ủ ộ ườ
kính.
Ví d : Đo n th ng CD là dây cung, đo n th ng AB là đng kính. ụ ạ ẳ ạ ẳ ườ
Toán 7 – H c Kì I – Nguy n Văn Quy n – 0938.59.6698 – s u t m và biên so nọ ễ ề ư ầ ạ
2. Tam giác
2.1. Đnh nghĩaị
-Tam giác ABC là hình g m ba đo n th ng AB, BC, CA khi A, B, C không ồ ạ ẳ
th ng hàng.ẳ
-Đi m M là đi m n m trong tam giác, đi m N là đi m n m ngoài tam giác. ể ể ằ ể ể ằ
2.2. Các y u tế ố
-Ba c nh: AB, BC, CAạ
-Ba góc:
B. Bài t p:ậ
D NG 1: ĐNG TRÒNẠ ƯỜ
Bài toán 1: Trên hình bên, ta có đng tròn (O; R)ườ
A. Đi m O cách m i đi m trên đng tròn m t kho ng R.ể ọ ể ườ ộ ả
B. Đi m O cách m i đi m trên hình tròn m t kho ng R.ể ọ ể ộ ả
C. Đi m O n m trên đng tròn ể ằ ườ
D. Ch có câu C đúng. ỉ
Bài toán 2: Cho

Toán 7 – H c Kì I – Nguy n Văn Quy n – 0938.59.6698 – s u t m và biên so nọ ễ ề ư ầ ạ
a) Nh ng đi m cách A m t kho ng 1,5cm thì n m đâu? Nh ng đi m cách B m t ữ ể ộ ả ằ ở ữ ể ộ
kho ng 2cm thì n m đâu? ả ằ ở
b) Có đi m nào v a cách A là 1,5cm; v a cách B là 2cm không? ể ừ ừ
Bài toán 3: Cho đo n th ng AB = 3cmạ ẳ
a) V đng tròn (A; 1,5cm) và đng tròn (B; 1cm). H i có đi m nào v a cách A ẽ ườ ườ ỏ ể ừ
là 1,5cm; v a cách B m t kho ng 1cm; ừ ộ ả
b) Hãy nêu b c v đi m M v a cách A là 3cm, v a cách B là 3cm. ướ ẽ ể ừ ừ
Bài toán 4: Cho đo n th ng AB = 4cm. Hãy d ng đng tròn tâm O nh n AB làm ạ ẳ ự ườ ậ
đng kính. ườ
Bài toán 5: Cho AB = 3cm, v đng tròn (A; 2,5cm) và đng tròn (B; 1,5cm), hai ẽ ườ ườ
đng tròn này c t nhau t i 2 đi m C, Dườ ắ ạ ể
a) Tính đ dài đo n th ng CA, CB, DA, DB;ộ ạ ẳ
b) T i sao đng tròn (B; 1,5cm) l i c t đo n th ng AB t i trung đi m I c a AB?ạ ườ ạ ắ ạ ẳ ạ ể ủ
c) Đng tròn (A; 2,5cm) c t đo n th ng AB t i K. Tính đ dài KB.ườ ắ ạ ẳ ạ ộ
Bài toán 6: V đng tròn tâm O bán kính 2cm. G i M là m t đi m n m ngoài đng ẽ ườ ọ ộ ể ằ ườ
tròn tâm O; OM c t đng tròn (O; 2cm) I, bi t OM = 3cm. ắ ườ ở ế
a) Tính IM
b) V đng tròn tâm I bán kính IM. Ch ng t đi m O n m ngoài đng tròn (I; ẽ ườ ứ ỏ ể ằ ườ
IM)
c) Đng tròn (I; IM) c t đng tròn (O; 2cm) P và Q, c t OM K. Ch ng t ườ ắ ườ ở ắ ở ứ ỏ
r ng đi m K n m trong đng tròn (O; 2cm). ằ ể ằ ườ
Bài toán 7: Cho hai đi m A, B cách nhau 3cm. V đng tròn (A; 2,5cm) và đng ể ẽ ườ ườ
tròn (B; 1,5cm). Hai đng tròn này c t nhau t i hai đi m C và D.ườ ắ ạ ể
a) Tính CA và DB.
b) T i sao (B; 1,5cm) c t đo n th ng AB t i trung đi m I c a AB. ạ ắ ạ ẳ ạ ể ủ
c) Đng tròn (A; 2,5cm) c t đo n th ng AB t i K. Tính KB. ườ ắ ạ ẳ ạ

Toán 7 – H c Kì I – Nguy n Văn Quy n – 0938.59.6698 – s u t m và biên so nọ ễ ề ư ầ ạ
Bài toán 8: Cho đo n th ng AB = 6cm. V đng tròn (A; 5cm) và đng tròn (B; ạ ẳ ẽ ườ ườ
3cm). Hai đng tròn này c t nhau t i M và N, các đng tròn tâm A và B theo th t ườ ắ ạ ườ ứ ự
c t đo n th ng AB t i C và Dắ ạ ẳ ạ
a) Tính AM, BM
b) Ch ng minh r ng D là trung đi m c a đo n ABứ ằ ể ủ ạ
c) Tính đ dài CDộ
Bài toán 9: V đng tròn .ẽ ườ
a) L y ba đi m A, B, C sao cho trong đó OA, OB là hai tia đi c a nhau trên ấ ể ố ủ
đng tròn. Hãy xác đnh v trí c a ba đi m trên đng tròn. ườ ị ị ủ ể ườ
b) Trên hình v có bao nhiêu dây cung, dây cung nòa l n nh t. Hãy k tênẽ ớ ấ ể
c) L y đi m D và E sao cho OD = 1,5cm, OE = 3cm. Hãy xác đnh v trí c a đi m Dấ ể ị ị ủ ể
và E đi v i đng tròn tâm O bán kính b ng 2 cm.ố ớ ườ ằ
Bài toán 10: V đng tròn (O; 2cm);ẽ ườ
a) L y đi m A b t kì trên đng tròn (O; 2cm), v đng tròn (A; 2cm ), đng ấ ể ấ ườ ẽ ườ ườ
tròn này c t đng tròn tâm O trên t i 2 đi m C, D;ắ ườ ở ạ ể
b) V đng tròn (C; 2cm);ẽ ườ
c) Ch ng t r ng đng tròn (C; 2cm) đi qua 2 đi m O, A. ứ ỏ ằ ườ ể
D NG 2: TAM GIÁCẠ
Bài toán 11: V tam giác ABC có:ẽ
a)
b) góc góc
c) Góc
Bài toán 12: V đo n th ng v đi m F sao cho và V tam giác EDF. Nói rõ cách v . ẽ ạ ẳ ẽ ể ẽ ẽ
Bài toán 13: Cho b n đi m A, B, C, D trong đó không có ba đi m nào th ng hàng. C ố ể ể ẳ ứ
qua ba đi m v m t tam giác. H i v đc m y tam giác, là nh ng tam giác nào? ể ẽ ộ ỏ ẽ ượ ấ ữ
Bài toán 14: Cho . Hãy v m t đng th ng d sao cho:ẽ ộ ườ ẳ

Toán 7 – H c Kì I – Nguy n Văn Quy n – 0938.59.6698 – s u t m và biên so nọ ễ ề ư ầ ạ
a) d không c t m t c nh nào c a tam giác? ắ ộ ạ ủ
b) d c t c ba c nh c a tam giácắ ả ạ ủ
Bài toán 15: Cho . Hãy v m t đng th ng d không đi qua các đnh c a m t tam giác ẽ ộ ườ ẳ ỉ ủ ộ
sao cho c t c ba tia AB, BC, CA.ắ ả
Bài toán 16: V đo n th ng IK sao cho V hai đng tròn và chúng c t nhau t i A ẽ ạ ẳ ẽ ườ ắ ạ
và B.
a) V và ẽ
b) Gi s chu vi là 8cm. Hãy tính chu vi và tính IK. ả ử
Bài toán 17: Cho tam giác ABC có , trên c nh AC l y đi m D (D không trùng v i A và ạ ấ ể ớ
C).
a) Tính đ dài AC, bi t AD = 4cm, CD = 3cm.ộ ế
b) Tính s đo c a bi t ố ủ ế
c) T B d ng tia Bx sao cho Tính s đo ừ ự ố
d) Trên c nh AB l y đi m E (E không trùng v i A và B). Ch ng minh r ng 2 đo n ạ ấ ể ớ ứ ằ ạ
th ngẳ
BD và CE c t nhau.ắ
Bài toán 18: Vẽ ΔABC. L y M là đi m trong c aấ ể ủ ΔABC. V các tia AM, BM, CM c t ẽ ắ
các c nh c aạ ủ ΔABC t ng ng t i các đi m N, P, Q. Vươ ứ ạ ể ẽ ΔNPQ. H i đi m M có n m ỏ ể ằ
trong ΔNPQ hay không?
Bài toán 19: V hình đ th y đc m i câu sau đây là saiẽ ể ấ ượ ỗ
a) Hình g m 3 đo n th ng đc g i là tam giácồ ạ ẳ ượ ọ
b) Hình g m 3 đo n th ng đôi m t c t nhau đc g i là tam giác.ồ ạ ẳ ộ ắ ượ ọ
c) Hình g m 3 đo n th ng đôi m t c t nhau t o ra 3 giao đi m (phân bi t) đc g i làồ ạ ẳ ộ ắ ạ ể ệ ượ ọ
tam giác.
d) Hình g m 3 đo n th ng AB, BC, CA đc g i là tam giác ABC.ồ ạ ẳ ượ ọ
e) Hình g m 3 đi m không th ng hàng A, B, C đc g i là tam giác ABC.ồ ể ẳ ượ ọ
f) M t đi m không thu c c nh c a tam giác ABC thì ph i n m trong tam giác đó.ộ ể ộ ạ ủ ả ằ


























