Những Người Biên Soạn
Đinh T n H ng, Đào Minh Quân,ấ ư
Nguy n Đ i L i,Tr n H ng Ni, ễ ạ ợ ầ ằ
Nguy n Th nh, Lê Huỳnh Đ c.ễ ị Ả ứ
PH N I:Ầ TH TÍCH HÌNH CHÓPỂ
Ba i 1: Cho hinh chop S.ABCD co đay la hinh vuông ABCD canh a,măt bên SAD la tam
giac đêu va năm trong mp vuông goc mp đay ABCD.Goi M,N,P lân l t la trung điêm ươ
cua SB,SC,SD.Tinh thê tich t diên CMNP. ư
Giai.
Goi H la trung điêm cua AD thi SH
⊥
AD.
Do (SAD)
⊥
(ABCD) nên suy ra SH
⊥
(ABCD)
Va SH =
3
2
a
(vi ABC la tam giac đêu canh a)
Ke MK//SH(K
HB),suy ra KM
⊥
(ABCD)va
MH=
2
SH
=
3
4
a
.
Vây VMCNP=
1
3
.S.CNP.MK=
1
3
.
2
8
a
.
3
4
a
.=
3
3
96
a
.
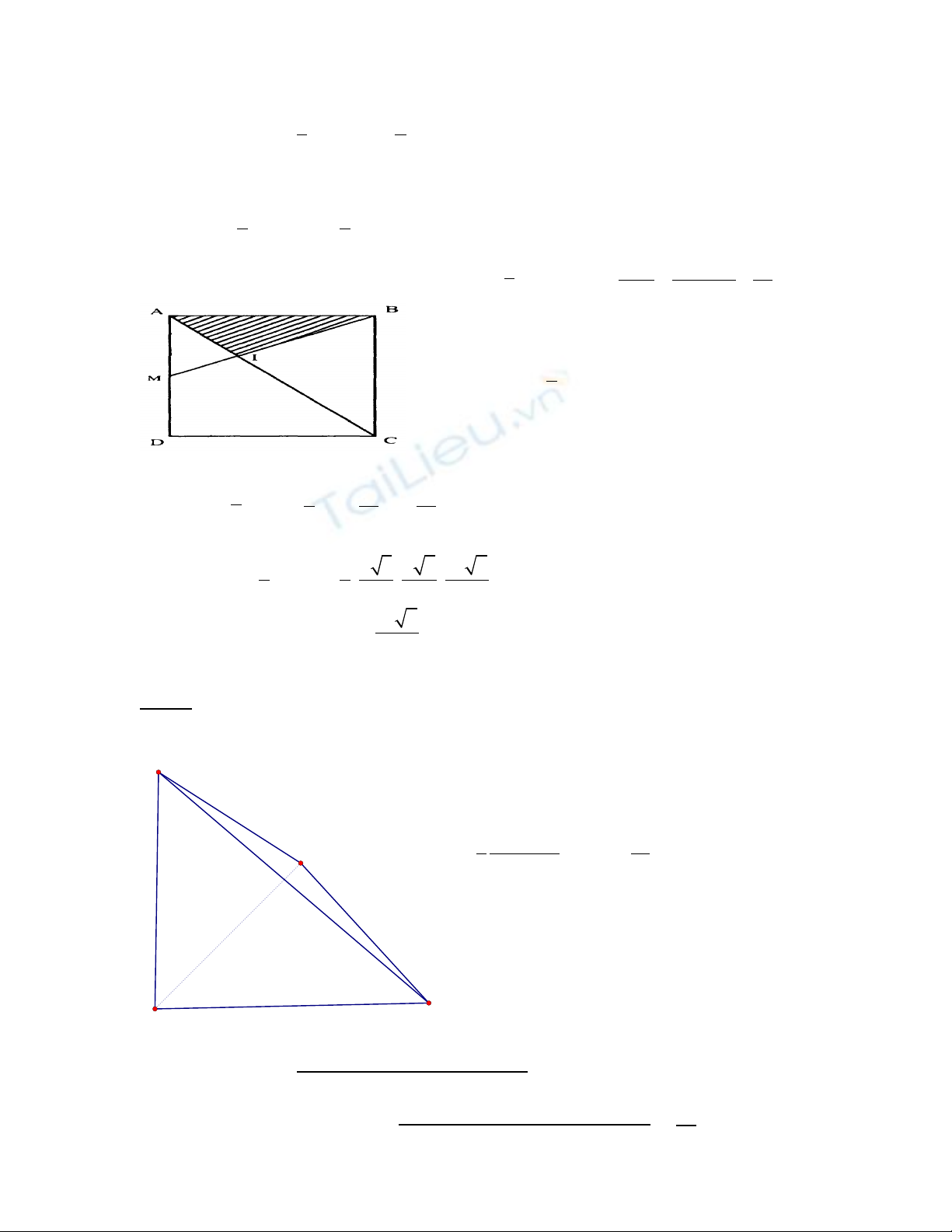
Ba i 2: Cho hinh chop S.SBCD co đays ABCD
la hinh ch nhât v i AB=a;AD=a ư ơ
2
;SA=a va
SA vuông goc mp (ABCD).Gia s I la giao ư
điêm cua BM va AC.Goi M,N lân l t la trung ươ
điêm cua AD va SC.Tim thê tich t diên ANIB. ư
Giai.
Goi O la tâm cua đay ABCD.Trong
,ta
co:NO la đ ng trung binh nên NO// SA,t c ươ ư
NO
⊥
(ABCD) va NO=
2
a
Ta co V.ANIB=V.NAIB=
1
3
.S.AIB.NO=
6
a
.S.AIB (1)
Ta tinh S.
AIBV
:
Xet hinh ch nhât (ABCD) .Do MA=MD ư
Suy ra:MA=
1
2
.BD
AI=
1
2
AC
AI=
1
3
.AC
2
AI
=
2
9
AC
=
2 2
2
9
a a+
=
2
3
a
Lai co:BI=
2
3
BM
Suy ra:BI2=
2
4
9
BM
=
2 2
2
4( ) 2
9 2 3
a a
a+ =
Do đo:AI2 +BI2 =AB2; Nên AIB la tam giac vuông đinh I ơ
Vây S.AIB=
2
1 1 3 6 2
. . . . .
2 2 3 3 6
a a a
AI BI= =
(2).
Thay (2) vao (1) ta co: V.ANIB=
.
Bai 3: Cho hinh chop S.SBC,đay ABC la tam giac cân đinh C,SA
⊥
(ABC).Gia s ư
SC=a;tim goc gi a 2 mp(SBC) va (ABD) sao cho thê tich khôi chop la l n nhât. ư ơ
Giai
Ta thây ngay
ˆ
SCA
α
=
,SA=SC
sin
α
va
AC=SC
cos
α
Suy ra V.SABC=
2 2 3
2
1 cos sin cos sin
3 2 6
a a
a
αα α α
=
(1)
T (1) suy ra :V.SABC nhan gia tri l n nhâtư ơ
khi va chi khi biêu th P= ư
2
cos sin
α α
nhan
GTLN.Vi
sin
α
>0 nên Pmax
P2max
2 2 2
(1 sin ) sin
α α
−
gia tri l n nhât. ơ
Ta co:
2 2 2
2 2 2
(1 sin )(1 sin )(2sin )
(1 sin ) sin 2
α α α
α α
− −
− =
Theo BĐT cô si thi:
2 2 2
2 2 2
(1 sin ) (1 sin ) 2sin
(1 sin )(1 sin )(2sin ) 3
α α α
α α α
� �
− + − +
− − � �
� �
=
8
27
A
C
B
S
Do đo :Pmax =
2 3
9
2 2
3
1 sin 2 sin 3
sin
α α α
− = =�
Vây VS.ABC nhân GTLN la
3 3
sin
27 3
a
α
=�
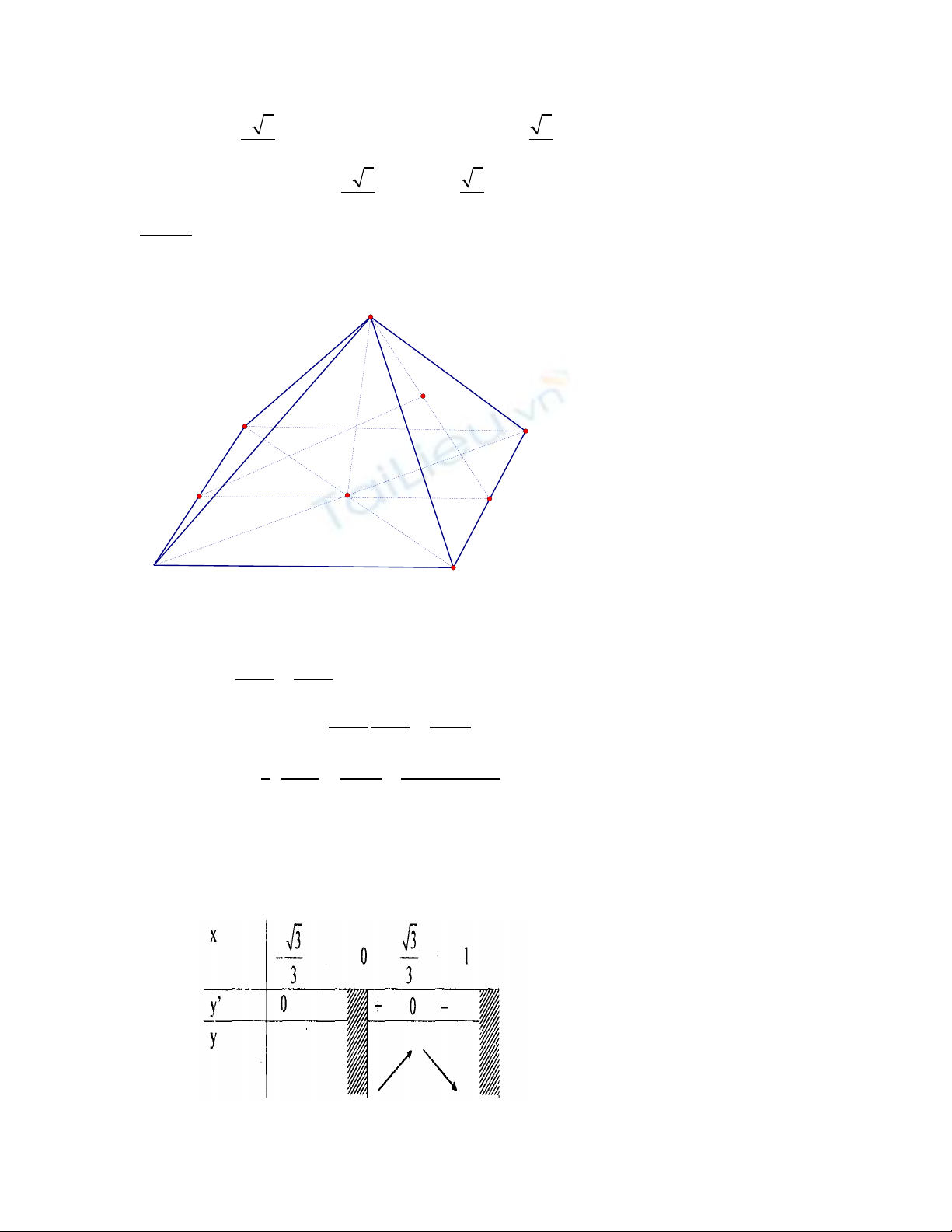
Bai 4: Cho hinh chop t giac đêu S.ABCD ma d(A;(SBC))=2a.V i gia tri nao cua ư ơ
α
(
α
la goc gi a mp bên va mp đay cua hinh chop)thi thê tich khôi chop la nho nhât?tim ư
GTNN đo.
Giai
N
M
o
D
S
B
C
H
Goi M,N.lân l t la trung điêm ươ
cua AD,BC;ke MH vuông goc SN(H
SN)
Ta co:
ˆ
SNM
α
=
.Do DA//BC suy ra AD//(SBC),suy ra d(M,(SBC))=MH=2a
Ta co :MN=
2
sin sin
MH a
α α
=
T đo :ư
2
tan sin sin cos
a a a
SO ON
αα α α
= = =
Do đo: V.SABCD=
2
2
2
1 2 4
( ) .
3 sin cos 3sin cos
a a a
α α α α
=
(1)
T (1) suy ra:VSABCD be nhât khi va chi khi ư
2
sin .cos
α α
l n nhât.ơ
Xet P=
2
sin .cos
α α
=
2 3
(1 cos ).cos cos cos
α α α α
− = −
(2)
T (2) dân đên xet ham sô:y=x-xư 3 (0<x<1)
Ta co :y’=1-3x2 va ta co bang biên thiên sau:
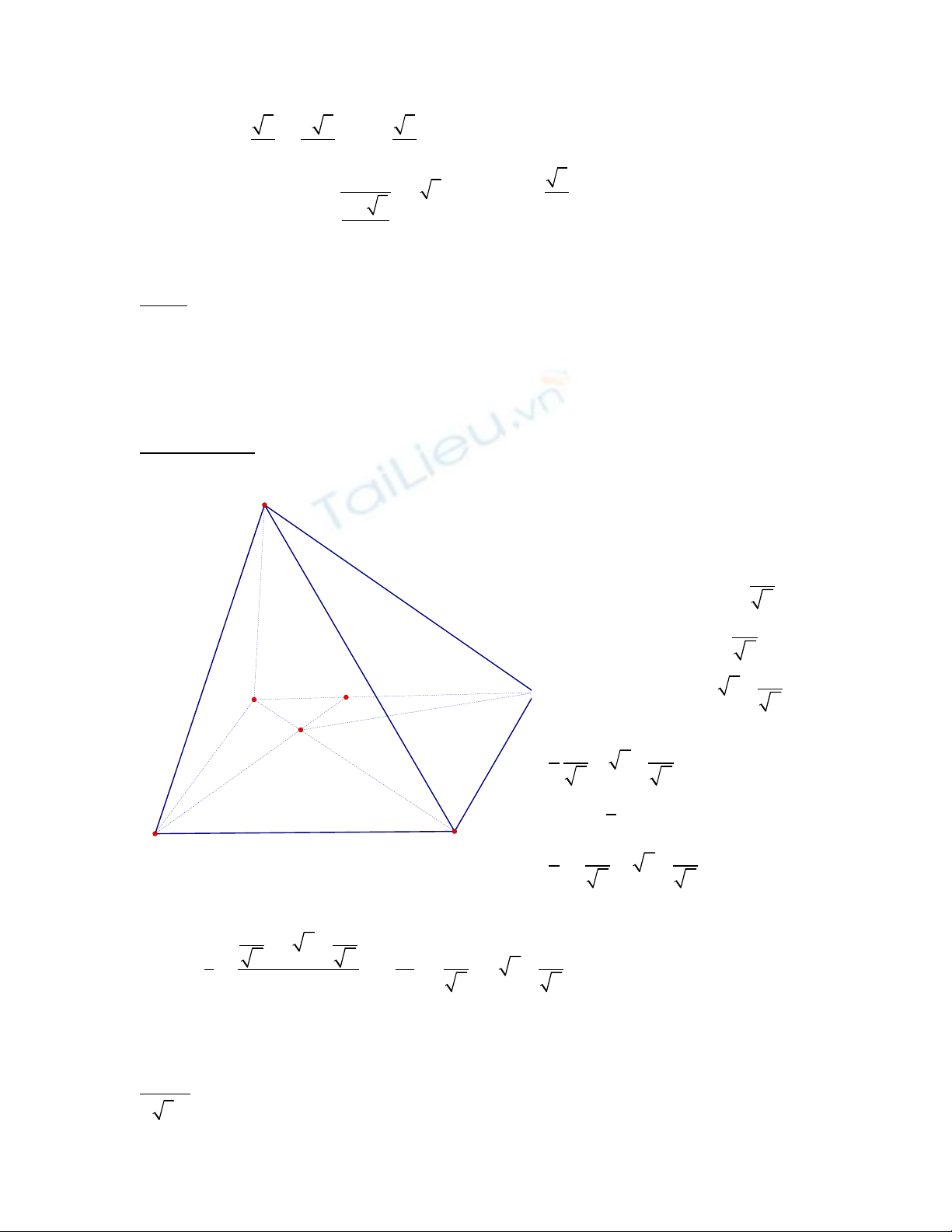
T đo yư max =y(
3 2 3 3
)
3 9 3
x= =�
Vây VSABCD min băng
3
3
4 3
2 3 cos 3
3.2 3
9
aa
α
= =�
Bai 5: Trên c nh AD c a hình vuông ABCD có đ dài là a, l y đi m M sao cho AM =ạ ủ ộ ấ ể
x (0 < x ≤ a).Trên đ ng th ng vuông góc v i m t ph ng (ABCD) t i A, l y đi m Sườ ẳ ớ ặ ẳ ạ ấ ể
sao cho SA = 2a.
a) Tính kho ng cách t đi m M đ n m t ph ng (SAC).ả ừ ể ế ặ ẳ
b) KÎ MH vu«ng gãc víi AC t¹i H . T×m vÞ trÝ cña M ®Ó thÓ tÝch khèi chãp
SMCH lín nhÊt.
Giai
Do SA
⊥
(ABCD) va SA
(SAC)
Suy ra (SAC)
⊥
(ABCD)
Lai co
MH
⊥
(SAC) suy ra d(M;
(SAC))=MH=AM
0
sin 45
=
2
x
Ta co:AH=
0
sin 45AM
=
2
x
Suy ra HC=AC-AH=
22
x
a−
SMHC=0.5.MH.MC=
1 1
( 2 )
22 2
xa−
VS.MCH=
1
3
SA.SMHC=
12 2
62 2
x x
a a
� �
−
� �
� �
T biêu th c trên ư ư
VS.MCH
2
3
2
12 2 2
3 2 6 2 2
x x
aa x x
a a x a M D
� �
+ −
� �
= − = =��� � �
� �
� �
� �
� �
Bai 6 Cho hình chóp S.ABCD có đáy ABCD là hình thoi ; hai đ ng chéo AC =ườ
2 3a
, BD = 2a và c t nhau t i O; hai m t ph ng (SAC) và (SBD) cùng vuông gócắ ạ ặ ẳ
H
B
C
A
D
S
M
v i m t ph ng (ABCD). Bi t kho ng cách t đi m O đ n m t ph ng (SAB)ớ ặ ẳ ế ả ừ ể ế ặ ẳ
b ng ằ
3
4
a
, tính th tích kh i chóp S.ABCD theo a.ể ố
Giai
T gia thiêt AC=ư
2 3a
;BD=2a va AC,BD cung vuông goc nhau tai trung điêm O cua
môi đ ng cheo.Ta co tam giac ABO vuông tai O va AO= ươ
3a
;BO=a.Do đo:
ˆ
ABD
=600,hay tam giac ABD đêu.
T gia thiêt suy ra 2 mp(SAC) va (SBD) cung vuông goc mp(ABCD) nên giao tuyên cuaư
chung la SO cung vuông goc (ABCD)
Do tam giac ABD đêu nên v i Hla trung điêm cua AB,Kla trung điêm cua HB,ta co ơ
DH
⊥
AB va DH=a
3
;OK//DH va OK=
13 ( )
2
DH a OK AB AB SOK= ⊥ ⊥� �
Goi I la hinh chiêu cua O lên SK,ta co AB
⊥
OI
( )OI SAB⊥�
hay OI la khoang cach t ư
O đên mp(SAB)
Tam giac SOK vuông tai O,OI la đ ng cao ươ
2 2 2
1 1 1
2
a
SO
OI OK SO
= + =� �
Diên tich đay:S ABCD=4.SABO=2.OA.OB=
2
2 3a
Đ ng cao khôi chop :SO=ươ
2
a
Thê tich khôi chop S.ABCD la:V SABCD=
1
3
SABCD.SO=
3
3
3
a
O
C
B
D
A
S
K
H
I