intTypePromotion=1
zunia.vn Tuyển sinh 2024 dành cho Gen-Z zunia.vn zunia.vn
ADSENSE
 » 
 » 

Chuyên đề nâng cao chủ đề đoạn thẳng, góc - Toán lớp 6

Chia sẻ: Tabicani09 | Ngày: | Loại File: PDF | Số trang:57

Thêm vào BST
Báo xấu
61
lượt xem 5
download
 
  Download Vui lòng tải xuống để xem tài liệu đầy đủ

Với mong muốn giúp các em học sinh dễ dàng hơn trong việc tìm kiếm tài liệu hoàn thành các bài tập. TaiLieu.VN mời các em cùng tham khảo Chuyên đề nâng cao 6 chủ đề đoạn thẳng, góc - Toán lớp 6. Nội dung tài liệu được tổng hợp và trình bày rõ ràng gồm 2 phần: tóm tắt lý thuyết bài học và bài tập. Hy vọng tài liệu sẽ giúp các em thuận tiện hơn trong việc tổng ôn lại kiến thức bài học và nâng cao kỹ năng giải bài tập.

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Chuyên đề nâng cao chủ đề đoạn thẳng, góc - Toán lớp 6

  1.  Sưu tầm CHUYÊN ĐỀ NÂNG CAO 6 CHỦ ĐỀ ĐOẠN THẲNG, GÓC Tài liệu sưu tầm, ngày 24 tháng 8 năm 2020
  2. NÂNG CAO VÀ PHÁT TRIỂN TOÁN 6 Website: tailieumontoan.com PHẦN: HÌNH HỌC Chương I. ĐOẠN THẲNG § 1. Điểm. Đường thẳng. Ba điểm thẳng hàng Kiến thức cơ bản: 1. Vị trí của điểm và đường thẳng (h.1) B - Điểm A thuộc đường thẳng a , kí hiệu A ∈ a - Điểm B không thuộc đường thẳng a , kí hiệu B∉a. a A 2. Ba điểm thẳng hàng khi chúng có cùng thuộc một đường thẳng. Ba điểm không thẳng hàng khi chúng Hình 1 không cùng thuộc bất kì đường thẳng nào. A M D 3. Trong ba điểm thẳng hàng, có một điểm và chỉ một điểm nằm giữa hai điểm còn lại. Trong hình 2, điểm M nằm giữa hai điểm A và B Hình 2 Nâng cao 1. Nếu có một điểm nằm giữa hai điểm khác thì ba điểm đó thẳng hàng. 2. Quan hệ ba điểm thẳng hàng còn được mở rộng thành nhiểu ( 4, 5,...) điểm thẳng hàng. 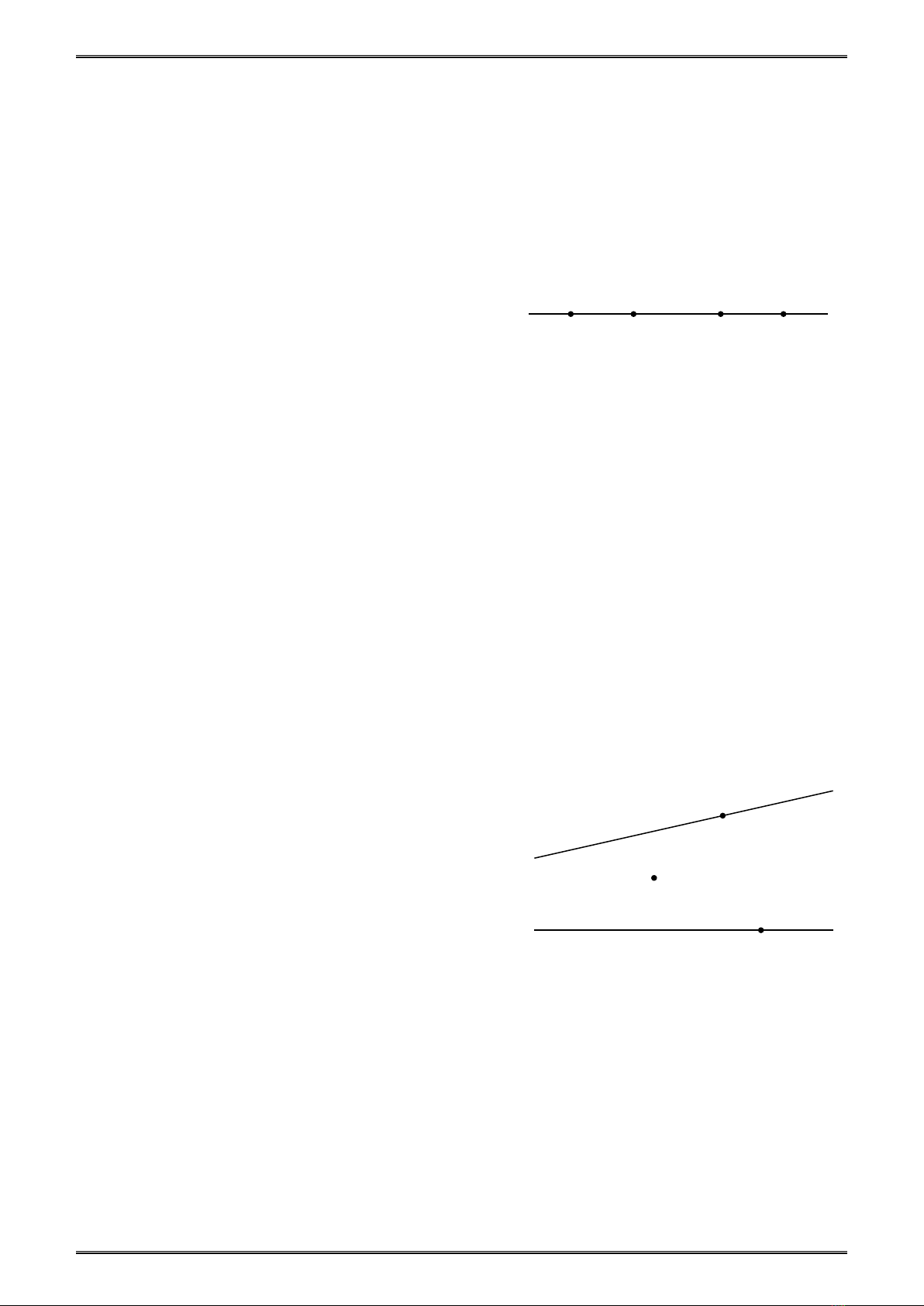Thí dụ 1: Trên đường thẳng a lấy 4 điểm A , B , C , D theo thứ tự đó. Lấy điểm M ∉ a . Hãy gọi tên: a) Tất cả các bộ 3 điểm không thẳng hàng; M b) Tất cả các bộ 3 điểm thẳng hàng; c) Tất cả các điểm nằm giữa điểm khác. Giải (h.3) a A B C D a) Các bộ ba điểm không thẳng hàng là: Hình 3 ( M , A, B ) ; ( M , A, C ) ; ( M , A, D ) ; ( M , B, C ) ; ( M , B, D ) ; ( M , C , D ) b) Các bộ ba điểm thẳng hàng là: ( A, B, C ) ; ( A, B, D ) ; ( A, C , D ) ; ( B, C , D ) c) B nằm giữa A và C ; B nằm giữa A và D ; C nằm giữa A và D ; C nằm giữa B và D . Nhận xét: Liên hệ tài liệu word toán SĐT hoặc zalo: 039.373.2038 -1-
  3. NÂNG CAO VÀ PHÁT TRIỂN TOÁN 6 Website: tailieumontoan.com Có bao nhiêu bộ 3 điểm thẳng hàng thì có bấy nhiêu trường hợp một điểm nằm giữa hai điểm khác. Thí dụ 2: Vẽ 4 điểm M , N , P , Q thẳng hàng sao cho đồng thời thỏa mãn 4 điều kiện sau: M không nằm giữa N và P (1) N không nằm giữa M và P (2) P không nằm giữa N và Q (3) M N P Q Q không nằm giữa N và P (4) Bằng lập luận hãy chứng tỏ rằng: Hình 4 a) Điểm P nằm giữa M và N b) Điểm N nằm giữa P và Q . Giải: (h.4) a) Xét 3 điểm thẳng hàng M , N , P thì: M không nằm giữa N và P (1) và N không nằm giữa M và P (2) vậy P nằm giữa M và N. b) P không nằm giữa N và Q (3) và Q không nằm giữa N và P (4) vậy N nằm giữa P và Q. BÀI TẬP 1. Trong hình 5 có hai đường thẳng m và n và ba điểm chưa đặt tên. Hãy điền các chữ A , B , C vào đúng vị trí của nó biết: a) Điểm A không thuộc đường thẳng m và cũng không thuộc đường thẳng n; m b) Điểm B không thuộc đường thẳng m ; c) điểm C không thuộc đường thẳng n . n 2. Vẽ các đường thẳng p và các điểm A , B trên p. Hình 5 a) Nêu cách vẽ điểm C thẳng hàng với 2 điểm A , B ; b) Nêu cách vẽ điểm D không thẳng hàng với 2 điểm A , B . 3. Hãy vẽ 5 điểm C , D , E , F , G không thẳng hàng nhưng ba điểm C , D , E , thằng; ba điểm E , F , G thẳng hàng. 4. Vẽ theo các cách diễn đạt sau: Liên hệ tài liệu word toán SĐT hoặc zalo: 039.373.2038 -2-
  4. NÂNG CAO VÀ PHÁT TRIỂN TOÁN 6 Website: tailieumontoan.com a) Điểm I nằm giữa hai điểm A và B ; điểm B nằm giữa I và K ; b) Hai điểm O , P không nằm cùng phía đối với Q ; hai điểm O và R nằm khác phía đối với Q nhưng P không nằm giữa O và R . 5. Cho ba điểm A , B , C ; mỗi điểm A , B đều không nằm giữa hai điểm còn lại. Hãy nêu điều kiện để: a) C nằm giữa A và B ; b) C không nằm giữa A và B . 6. Trái đất quay quanh Mặt Trời: Mặt Trăng quay xung quanh Trái Đất. Mặt Trời chiếu sáng tới Trái Đất và Mặt Trăng. Khi ba thiên thể này thẳng hàng thì xảy ra nhật thực hoặc nguyệt thực (là hiện tượng mặt trời hoặc mặt trăng đang sáng bỗng nhiên bị che lấp và tối đi). Hỏi: a) Khi xảy ra nhật thực thì Mặt Trăng ở vị trí nào? b) Khi xảy ra nguyệt thực thì Trái Đất ở vị trí nào? 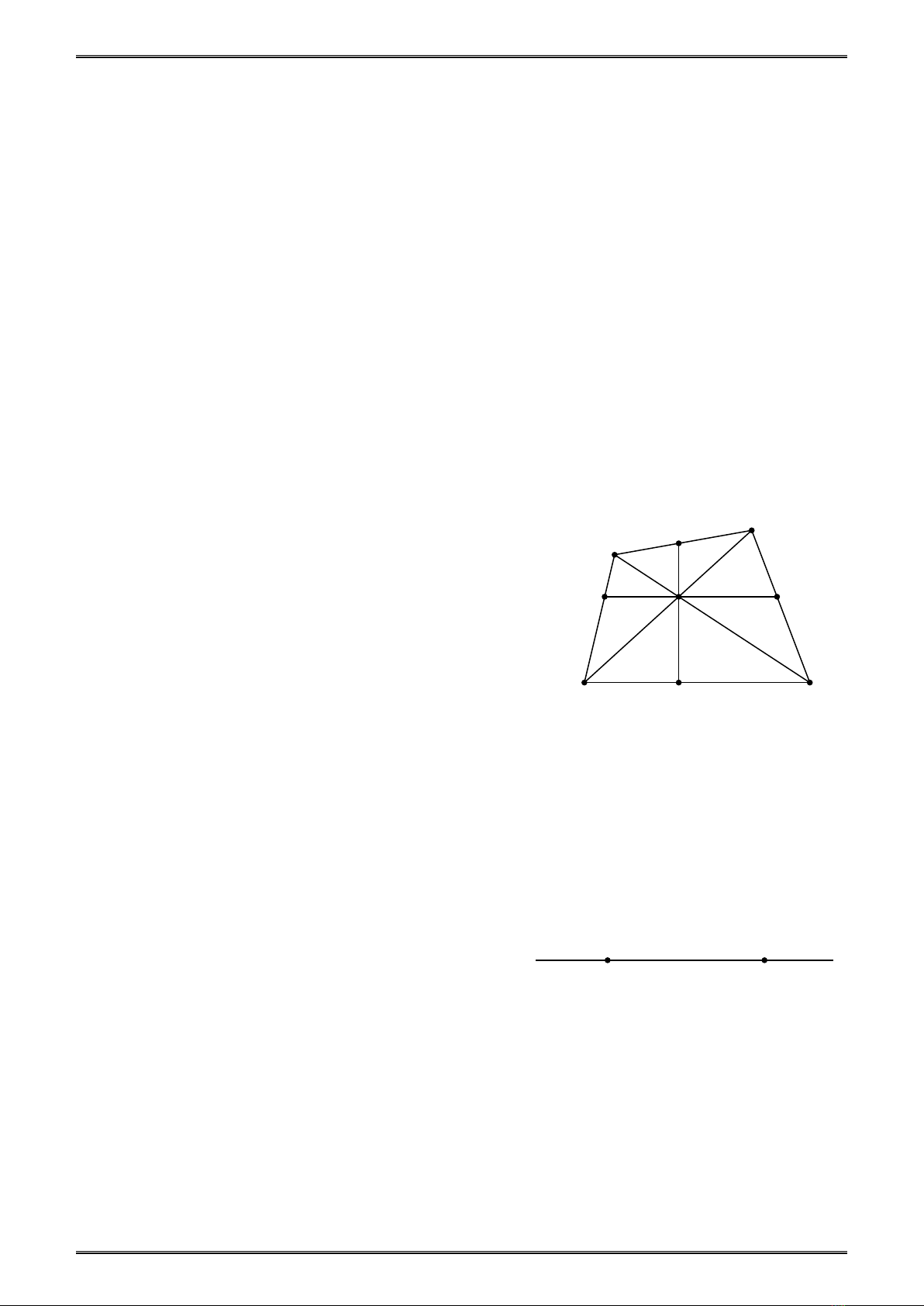B M 7. Xem hình 6 rồi cho biết: Có bao nhiêu trường hợp A một điểm nằm giữa hai điểm khác? E F 8. Theo hình 6, ta có thể trồng được 9 cây thành 8 hàng, mỗi hàng 3 cây. Hãy vẽ sơ đồ trồng 9 câu O thành: a) 9 hàng, mỗi hàng 3 cây; D N C b) 10 hàng, mỗi hàng 3 cây. Hình 6 § 2. Đường thẳng đi qua hai điểm Kiến thức cơ bản: 1. Có một đường thẳng và chỉ một đường thẳng đi qua hai điểm A và B (h.7). 2. Ba cách đặt tên đường thẳng: A B - Dùng một chữ cái in thường, ví dụ a - Dùng hai chữ cái in thường, ví dụ xy Hình 7 - Dùng hai chữ cái in hoa, ví dụ AB 3. Vị trí của hai đường thẳng phân biệt: - Hoặc không có điểm chung nào (gọi là hai đường thẳng song song. Ví dụ hai đường thẳng a , b trong hình 8. Liên hệ tài liệu word toán SĐT hoặc zalo: 039.373.2038 -3-
  5. NÂNG CAO VÀ PHÁT TRIỂN TOÁN 6 Website: tailieumontoan.com - Hoặc chỉ có một điểm chung nào (gọi là hai đường thẳng cắt nhau). Ví dụ hai đường thẳng m và n trong hình 9. m b O a n Hình 8 Hình 9 Nâng cao: 1. Muốn chứng minh hai hay nhiều đường thẳng trùng nhau ta chỉ cần chứng tỏ chúng có 2 điểm chung. 2. Ba (hay nhiều) đường thẳng cùng đi qua một điểm gọi là ba (hay nhiều) đường thẳng đồng quy. Muốn chứng minh nhiều đường thẳng đồng quy ta có thể xác định giao điểm của hai đường thẳng nào đó rồi chứng minh các đường thẳng còn lại nếu đều đi qua giao điểm này. Thí dụ 3: Cho trước 12 điểm trong đó không có 3 điểm nào thẳng hàng, Vẽ các đường thẳng đi qua các cặp điểm. a) Hỏi vẽ được bao nhiêu đường thẳng? b) Nếu thay 12 điểm bằng n điểm ( n ∈  ; n ≥ 2 ) thì vẽ được bao nhiêu đường thẳng? Giải: a) Chọn một trong số 12 điểm đã cho rồi nối điểm đó với 11 điểm còn lại ta được 11 đường thẳng. Làm như vậy với tất cả 12 điểm ta được 11.12 đường thẳng. Nhưng như thế thì mỗi đường thẳng đã được tính 2 lần (vì đường thẳng AB với đường 11.12 thẳng BA chỉ là một) do đó thực sự chỉ có = 66 (đường thẳng). 2 n ( n − 1) b) Cũng lập luận như trên, với n điểm thì số đường thẳng vẽ được là . 2 Nhận xét: n ( n − 1) - Với n là số điểm cho trước thì công thức giúp ta tính được số đường 2 thẳng đi qua tất cả các cặp điểm. Liên hệ tài liệu word toán SĐT hoặc zalo: 039.373.2038 -4-
  6. NÂNG CAO VÀ PHÁT TRIỂN TOÁN 6 Website: tailieumontoan.com - Ngược lại, với n là số đường thẳng cho trước (đôi một cắt nhau và không có ba n ( n − 1) đường thẳng nào đồng quy) thì công thức giúp ta tính được số giao điểm 2 của tất cả các cặp đường thẳng. Thí dụ 4: Cho 4 điểm A , B , C , D trong đó ba điểm A , B , C , thẳng hàng, ba điểm B , C , D thẳng hàng. Chứng tỏ rằng 4 điểm A , B , C , D thẳng hàng. Giải: Ba điểm A , B , C , thẳng hàng nên chúng cùng nằm trên một đường thẳng. Ba điểm B , C , D thẳng hàng nên chúng cùng nằm trên một đường thẳng. Hai đường thẳng này có hai điểm chung là B và C nên chúng phải trùng nhau, suy ra 4 điểm A , B , C , D thẳng hàng. BÀI TẬP 9. Cho trước hai điểm A và B . a) Hãy vẽ đường thẳng m đi qua A và B b) Hãy vẽ đường thẳng n đi qua A nhưng không đi qua B c) Hãy vẽ đường thẳng p không có điểm chung nào với đường thẳng m . 10. Cho trước 4 điểm A , B , C , D trong đó không có ba điểm nào thẳng hàng. Tìm M sao cho ba điểm M , A , B thẳng hàng; ba điểm M , C , D thẳng hàng. 11. Cho trước 6 điểm. Vẽ các đường thẳng đi qua các cặp điểm. a) Nếu trong 6 điểm đó không có ba điểm nào thẳng hàng thì sẽ vẽ được bao nhiêu đường thẳng? b) Nếu trong 6 điểm đó có đúng 3 điểm thẳng hàng thì sẽ vẽ được bao nhiêu đường thẳng? 12. Giải bóng đá vô địch quốc gia hạng chuyên nghiệp có 12 đội tham gia đấu vòng tròn hai lượt đi và về. Tính tổng số trận đấu. 13. Cho trước một số điểm trong đó không có ba điểm nào thẳng hàng. Vẽ các đường thẳng đi qua các cặp điểm. Biết tổng số đường thẳng vẽ được là 36 . Tính số điểm cho trước. 14. Có một số con đường (thẳng), chúng cắt nhau đôi một và không có ba đường nào đồng quy. Các con đường đó cắt nhau tạo thành 300 ngã tư. Hỏi có tất cả bao nhiêu con đường? 15. Cho 11 đường thẳng đôi một cắt nhau. a) Nếu trong số đó không có ba đường thẳng nào đồng quy thì có tất cả bao nhiêu giao điểm của chúng? Liên hệ tài liệu word toán SĐT hoặc zalo: 039.373.2038 -5-
  7. NÂNG CAO VÀ PHÁT TRIỂN TOÁN 6 Website: tailieumontoan.com b) Nếu trong 11 đường thẳng đó có đúng 5 đường thẳng đồng quy thì có tất cả bao nhiêu giao điểm của chúng? 16. Cho ba đường thẳng m , a , b đồng quy tại O ; ba đường thẳng n , a , b cũng đồng quy. a) Chứng minh rằng cả 4 đường thẳng m , n , a , b đồng quy tại O b) Vẽ thêm hai đường thẳng c , d không đi qua O . Hỏi 6 đường thẳng m , n , a , b , c , d có nhiều nhất là bao nhiêu giao điểm? 17. Cho trước n điểm trong đó không có ba điểm nào thẳng hàng. Vẽ các đường thẳng đi qua các cặp điểm. Tìm n biết rằng nếu có thêm 1 điểm (không thẳng hàng với bất kì 2 điểm nào trong số n điểm đã cho) thì số đường thẳng vẽ được tăng thêm là 8 . § 3. Tia Kiến thức cơ bản: 1. Hình gồm điểm O và một phần đường thẳng bị chia ra bởi điểm O được gọi là một tia gốc O . 2. Hai tia chung gốc tạo thành đường thẳng được gọi là hai tia đối nhau. Nhận xét: x O y Mỗi điểm trên đường thẳng là gốc chung nhau của hai tia đối nhau. Trong hình 10, hai tia Ox , Oy đối Hình 10 nhau. O M x 3. Điểm M thuộc tia Ox ( M ≠ O ) thì hai tia OM , Ox trùng nhau. (h.11). Hình 11 Nâng cao: Quan hệ giữa một điểm nằm giữa hai điểm với hai tia đối nhau, hai tia trùng nhau: Xét 3 điểm A , O , B thẳng hàng. 1. Nếu hai tia OA , OB đối nhau thì gốc O nằm giữa A và B . A O B 2. Ngược lại, Nếu O nằm giữa A và B thì: Hình 12 - Hai tia OA , OB đối nhau - Hai tia AO , AB trùng nhau: hai tia BO , BA trùng nhau. Thí dụ 5: Liên hệ tài liệu word toán SĐT hoặc zalo: 039.373.2038 -6-
  8. NÂNG CAO VÀ PHÁT TRIỂN TOÁN 6 Website: tailieumontoan.com Cho điểm O nằm giữa hai điểm A và B ; điểm M nằm giữa hai điểm A và O ; điểm N nằm giữa hai điểm B và O . a) Nêu tên các tia trùng nhau gốc O . b) Chứng tỏ rằng điểm O nằm giữa hai điểm M , N . Giải: (h.13) a) Điểm M nằm giữa hai điểm A và O nên hai tia OA , OM trùng nhau (1) Điểm N nằm giữa hai điểm B và O nên hai tia OB , ON trùng nhau A M O N B (2) b) Điểm O nằm giữa hai điểm A và Hình 13 B nên hai tia OA , OB đối nhau (3). Từ (1); (2); (3) suy ra hai tia OM , ON đối nhau do đó điểm O nằm giữa hai điểm M và N . Nhận xét: 1. Để chứng minh điểm O nằm giữa hai điểm M và N ta dùng phương pháp xét các tia gốc O . 2. Thí dụ 5 cho ta một dấu hiệu nhận biết z một điểm nằm giữa hai điểm khác. BÀI TẬP 18. Xem hình 14 rồi cho biết: H a) Những tia nào chung gốc O ? b) Hai tia nào đối nhau? x O y c) Hai tia nào trùng nhau? Hình 14 19. Cho đường thẳng xy . Lấy điểm O ∉ xy ; điểm A ∈ xy và điểm B trên tia Ay ( B khác A ) a) Kể tên các tia đối nhau, các tia trùng nhau; b) Kể tên hai tia không có điểm chung; c) Gọi M là một điểm di động trên xy . Xác định vị trí của M để cho tia Ot đi qua M không cắt hai tia Ax , By . 20. Vẽ hai đường thẳng mn và xy cắt nhau tại O . a) Kể tên các tia đối nhau; b) Trên tia Ox lấy điểm P , trên tia Om lấy điểm E ( P và E khác O ). Hãy tìm vị trí của Q để điểm O nằm giữa P và Q ; tìm vị trí của F để hai tia OE , OF trùng nhau. Liên hệ tài liệu word toán SĐT hoặc zalo: 039.373.2038 -7-
  9. NÂNG CAO VÀ PHÁT TRIỂN TOÁN 6 Website: tailieumontoan.com 21. Trên đường thẳng xy lấy một điểm O . Lấy điểm A trên tia Ox , điểm B trên tia Oy , điểm M nằm giữa O và A . Giải thích vì sao: a) Hai tia OA , OB đối nhau? b) Điểm O nằm giữa hai điểm M và B ? 22. Cho 4 điểm A , B , C và O . Biết hai tia OA , OB đối nhau; hai tia OA, OC trùng nhau. a) Giải thích vì sao 4 điểm A , B , C , O thẳng hàng. b) Nếu điểm A nằm giữa C và O thì điểm A có nằm giữa hai điểm B và C không? Vì sao? 23. Cho điểm O nằm giữa hai điểm A và B ; điểm I nằm giữa hai điểm O và B . Giải thích vì sao: a) O nằm giữa A và I ? b) I nằm giữa A và B ? § 4. Đoạn thẳng. Độ dài đường thẳng. Cộng độ dài hai đường thẳng Kiến thức cơ bản: 1. Đoạn thẳng AB là hình gồm điểm A , điểm B và tất cả các điểm nằm giữa hai điểm A và B (h.15) 2. Mỗi đoạn thẳng có một độ dài. Độ dài đoạn thẳng là một số dương. 3. AB = CD ⇔ AB và CD có cùng độ dài; A B AB < CD ⇔ AB ngắn hơn CD ; AB > CD ⇔ AB dài hơn CD . Hình 15 4. Nếu điểm M nằm giữa hai điểm A và B thì AM + MB = AB . A M B Ngược lại, nếu AM + MB =AB thì điểm M nằm giữa Hình 16 hai điểm A và B (h.16). Nâng cao : 1. Mệnh đề sau tương đương với tính chất trên : Nếu AM + MB ≠ AB thì điểm M không nằm giữa A và B . 2. Cộng liên tiếp (h.17) Liên hệ tài liệu word toán SĐT hoặc zalo: 039.373.2038 -8-
  10. NÂNG CAO VÀ PHÁT TRIỂN TOÁN 6 Website: tailieumontoan.com Nếu điểm M nằm giữa hai điểm A và B ; điểm N nằm giữa M và B . A M N B Thì AM + MN + NB = AB . Hình 17 Thí dụ 6 : Cho điểm M nằm giữa hai điểm A và B . Giải thích vì sao AM < AB ; MB < AB . Giải : (h.18) Vì điểm M nằm giữa hai điểm A và B nên AM + MB = AB A M B Do AM > 0 ; BM > 0 nên AM < AB ; BM < AB . Hình 18 Thí dụ 7 : Cho ba điểm M , O , N thẳng hàng. Điểm N không nằm giữa hai điểm M và O . Cho biết MN = 3cm ; ON = 1cm , hãy so sánh OM với ON . Giải : (h.19) Nếu điểm M nằm giữa hai điểm O và N thì O M N OM + MN = ON . Thay số : OM + 3 = 1 (vô lí) Vậy điểm M không 3cm 1cm nằm giữa giữa O và N . Hình 19 Điểm N không nằm giữa M và O (đề bài) Suy ra điểm O nằm giữa hai điểm M và N . Ta có : MO + ON = MN ; MO + 1 =3 ; MO = 2 (cm). Do đó OM > ON (vì 2 > 1 ). Nhận xét : Trong cách giải của ví dụ này, để tìm ra điểm O nằm giữa hai điểm M và N ta đã dùng phương pháp loại trừ. Trong ba điểm M , O , N thẳng hàng có một và chỉ một điểm nằm giữa hai diểm khác. Điểm N không nằm giữa hai điểm còn lại (đề bài). Điểm M không nằm giữa hai điểm còn lại (tìm ra được nhờ phương pháp phản chứng). Vậy điểm O phải nằm giữa hai điểm còn lại. BÀI TẬP 24. Cho 5 điểm A , B , C , D , E trong đó không có ba điểm nào thẳng hàng. Vẽ các đoạn thẳng đi qua các cặp điểm. Hỏi vẽ được bao nhiêu đoạn thẳng, là nhưng đoạn thẳng nào ? Kết quả trên có thay đổi nếu cả 5 điểm A , B , C , D , E thẳng hàng ? Liên hệ tài liệu word toán SĐT hoặc zalo: 039.373.2038 -9-
  11. NÂNG CAO VÀ PHÁT TRIỂN TOÁN 6 Website: tailieumontoan.com 25. Cho trước n điểm ( n ∈  ; n ≥ 2 ) Vẽ các đoạn thẳng đi qua các cặp điểm được tất cả 28 đoạn thẳng. Tìm n . 26. Vẽ 5 đoạn thẳng đôi một cắt nhau sao cho tổng số giao điểm là 10. GIải thích vì sao số giao điểm không thể quá 10 ? 27. Xem hình 20 rồi cho biết a) Hình này có mấy tia ? x' b) Hình này có mấy đoạn thẳng ? C c) Những cặp đoạn thẳng nào không cắt nhau ? B d) Vì sao có thể khẳng định tia Ox không cắt đoạn thẳng BC ? A x O y D Hình 20 y' 28. Cho hai tia chung gốc Ox , Oy . Trên tia Ox lấy hai điểm B và C sao cho B nằm giữa O và C Trên tia Oy lấy điểm A sao cho OA > OC . a) So sánh OA với OB . b) So sánh OA − OB với OB . 29. Trên đường thẳng a lấy 4 điểm E , F , G , H theo thứ tự đó. Giả sử EH = 7cm ; EF = 2cm ; FG = 3cm a) So sánh FG với GH . b) Tìm những cặp đoạn thẳng bằng nhau. 30. Cho đoạn thẳng AB . Trên tia đối của tia AB lấy điểm E , trên tia đối của tia BA lấy điểm F sao cho AE < BF . Hãy so sánh AF với BE . 31. Cho ba điểm A , B , C . a) Giả sử AB = 2cm ; BC = 3cm ; CA = 5cm , hãy chứng tỏ A , B , C thẳng hàng. b) Giả sử AB = 2cm ; BC = 3cm ; CA = 4cm , hãy chứng tỏ A , B , C không thẳng hàng. 32. Cho đoạn thẳng AB . Lấy điểm O nằm giữa A và B , Lấy điểm I nằm giữa O và B . a) Giả sử AB = 5cm ; AO = 2cm ; BI = 2cm , Tính OI . b) Giả sử AO = a ; BI = b , tìm điều kiện của a và b để AI = OB . Liên hệ tài liệu word toán SĐT hoặc zalo: 039.373.2038 -10-
  12. NÂNG CAO VÀ PHÁT TRIỂN TOÁN 6 Website: tailieumontoan.com §5. Vẽ đoạn thẳng cho biết độ dài Kiến thức cơ bản: 1. Trên tia Ox bao giờ cũng vẽ được một và a chỉ một điểm M sao cho OM = a (đơn vị dài) (h.21). x 2. Trên tia Ox , OM = a , ON = b nếu 0 < a < b O M thì điểm M nằm giữa hai điểm O và N (h.22). Hình 21 Nâng cao: Trên toa Ox có ba điểm M , N , P ; OM = a ; ON = b ; OP = c nếu 0 < a < b thì điểm N nằm giữa hai điểm M và P (h.23) (xem ví dụ 9). b c b x x O N M P M O N a a Hình 22 Hình 23 Thí dụ 8 : Trên tia Ox lấy điểm P và Q sao cho OP = 3cm ; PQ = 2cm . Tính OQ . Giải : (h.24a, b) Ta xét hai trường hợp : 3cm 2cm a) Trường hợp Q nằm trên tia đối của tia x PO (h.24a) lúc đó P nằm giữa hai điểm Q O P O và Q , suy ra OQ = OP + PQ = 3 + 2 = 5 (cm). Hình 24a b) Trường hợp Q nằm trên tia PO (h.24b) 3 Vì PQ < PO(2 < 3) nên Q nằm giữa P và x O do đó PQ + QO = PO P O Q 2 Suy ra OQ = OP − PQ = 3 − 2 = 1 (cm). Hình 24b Nhận xét : Trên tia Ox lấy P sao cho OP = 3cm, điểm P là điểm duy nhất, còn điểm Q thì không duy nhất. Tại sao như vậy ? Liên hệ tài liệu word toán SĐT hoặc zalo: 039.373.2038 -11-
  13. NÂNG CAO VÀ PHÁT TRIỂN TOÁN 6 Website: tailieumontoan.com Điểm Q không duy nhất trên tia Ox vì điểm Q không cạc gốc O của tia Ox một khoảng 2cm mà cách P một khoảng PQ = 2cm ; điểm P chỉ là một điểm thuộc tia Ox chứ P không phải là gốc của tia Ox . Thí dụ 9 : Gọi M , N , P là ba điểm trên tia Ox ; OM = a ; ON = b ; OP = c ; Giải thích vì sao nếu a < b < c thì điểm N nằm giữa hai điểm M và P . Giải: (h.25) Hai điểm M , N thuộc tia Ox mà c OM < ON (a < b) nên điểm M nằm b giữa hai điểm O và N suy ra hai tia x O M N P NM , NO trùng nhau (1) a Hai điểm N và P thuộc tia Ox mà ON < OP (b < c) nên điểm N nằm Hình 25 giữa hai điểm O và P , suy ra hai tia NO và NP đối nhau (2) Từ (1) và (2) suy ra hai tia NM , NP đối nhau, do đó điểm N nằm giữa hai điểm M và P . BÀI TẬP 33. Gọi M , N , P là ba điểm trên tia Ox sao cho OM = 2cm , ON = 3cm , OP = 5cm . So sánh MN và NP . 34. Gọi A và B là hai điểm trên tia Ox sao cho OA = 4cm ; OB = 6cm . Trên tia BA lấy điểm C sao cho BC = 3cm . So sánh AB với AC . 35. Cho A và B là hai điểm trên tia Ox sao cho OA = a (cm) với a > 0 ; AB = 2cm .Tính OB. 36. Vẽ đoạn thẳng AB = 5cm . Lấy hai điểm E và F nằm giữa A và B sao cho AE + BF = 7cm . a) Chứng tỏ rằng điểm E nằm giữa hai điểm B và F . b) Tính EF . 37. Vẽ hai tia chung gốc Ox , Oy . Trên tia Ox lấy hai điểm A và B (điểm A nằm giữa O và B ). Trên tia Oy lấy hai điểm M và N sao cho OM = OA ; ON = OB . a) Chứng tỏ rằng điểm M nằm giữa O và N ; b) So sánh AB với MN . 38*. Trên đoạn thẳng AB lấy hai điểm O và I sao cho OA < OB và AI > IB . Hỏi trong các bộ ba điểm A , O , I và B , O , I điểm nào nằm giữa hai điểm còn lại ? Liên hệ tài liệu word toán SĐT hoặc zalo: 039.373.2038 -12-
  14. NÂNG CAO VÀ PHÁT TRIỂN TOÁN 6 Website: tailieumontoan.com §6. Trung điểm của đoạn thẳng Kiến thức cơ bản : 1. Trung điểm của đoạn thẳng là điểm nằm giữa hai đầu đoạn thẳng và cách đều hai đầu đọa thẳng đó (h.26). 2. Nếu M là trung điểm của đoạn A M B AB = MB thẳng AB thì: MA = . 2 Hình 26 Nâng cao : AB 1. Nếu M nằm giữa hai đầu đoạn thẳng AB và AM = thì M là trung điểm của AB . 2 (Xem thí dụ 11). 2. Mỗi đoạn thẳng đều có một trung điểm duy nhất. Thí dụ 10 : Cho đoạn thẳng AB = a . Điểm O nằm giữa A và B Gọi M và N thứ tự là trung điểm của OA và OB . Tính MN . Giải. (h.27) M là trung điểm của OA nên M nằm a AO giữa A và O ; OM = . ? 2 N là trung điểm của OB nên N nằm OB A M O N B giữa O và B ; ON = . 2 Hình 27 Vì có O nằm giữa A và B (đề bài) nên O nằm giữa M và N (xem ví dụ 5 ). AO OB AO + OB AB a Vậy MN = OM + ON = + = = hay MN = . 2 2 2 2 2 Nhận xét: Độ dài MN là một số không đổi, nó phụ thuộc vào vị trí của điểm O trên đoạn thẳng AB . AB Ta luôn có MN = . 2 Thí dụ 11: AB Cho điểm M nằm giữa hai đầu đoạn thẳng AB và AM = . Giải thích vì sao M là trung 2 điểm của AB . Liên hệ tài liệu word toán SĐT hoặc zalo: 039.373.2038 -13-
  15. NÂNG CAO VÀ PHÁT TRIỂN TOÁN 6 Website: tailieumontoan.com Giải. (h.28) Điểm M nằm giữa A và B (1) M B A Nên AM + MB = AB = AB − AM MB Hình 28 AB AB MB = AB − = 2 2 Do đó AM = MB. ( 2) Từ (1) và ( 2 ) suy ra M là trung điểm của AB . BÀI TẬP 39. Cho ba điểm M , N , O sao cho OM = 2cm ; ON = 2cm và MN = 4cm . Vì sao có thể khẳng định O là trung điểm của đoạn MN . 40. Trên tia Ox lấy hai điểm A và M sao cho OA = 3cm , OM = 4,5cm . Trên tia Ax lấy điểm B sao cho M là trung điểm của AB . Hỏi điểm A có phải là trung điểm của đoạn thẳng OB không? Vì sao? 41. Trên đường thẳng a lấy 6 điểm M , N , O, P, Q, R theo thứ tự đó. Biết rằng MN= NO = OP= PQ= = QR . Tìm những điểm là trung điểm của đoạn thẳng. 42. Cho đoạn thẳng AB = 6cm . Lấy hai điểm C , D thuộc đoạn thẳng AB sao cho = BD AC = 2cm . Gọi M là trung điểm của AB . a) Giải thích tại sao M cũng là trung điểm của CD . b) Tìm trên hình vẽ những điểm khác cũng là trung điểm của đoạn thẳng. 43. Trên tia Ax lấy hai điểm O và B sao cho AO = 2cm ; AB = 5cm . Gọi I là trung điểm của OB . Tính AI . 44. Trên đường thẳng xy lấy một điểm O và hai điểm M , N sao cho OM = 2cm ; ON = 3cm . Vẽ các điểm A và B trên đường thẳng xy sao cho M là trung điểm của OA ; N là trung điểm của OB . Tính độ dài AB. 45 * . Cho đoạn thẳng AB và trung điểm M của nó. Lấy điểm O thuộc tia đối của tia BA ( O khác B ). Hãy so sánh OM với trung bình cộng của hai đoạn thẳng OA, OB . 46 * . Cho đoạn thẳng AB = 2100 ( cm ) . Gọi M 1 là trung điểm của đoạn thẳng AB ; gọi M 2 là trung điểm của đoạn thẳng M 1B ; gọi M 3 là trung điểm của đoạn thẳng M 2 B,..., gọi M 100 là trung điểm của đoạn thẳng M 99 B . Tính độ dài của đoạn thẳng M 1M 100 . Liên hệ tài liệu word toán SĐT hoặc zalo: 039.373.2038 -14-
  16. NÂNG CAO VÀ PHÁT TRIỂN TOÁN 6 Website: tailieumontoan.com § 7. Ôn tập chương I Thí dụ 12. Cho 4 điểm A, B, M , N sao cho hai tia MA, MN đối nhau; hai tia NM , NB đối nhau và AM = a ; BN = b ( a < b ) . a) Bốn điểm A, B, M , N có thẳng hàng b a không? Vì sao? A N B b) So sánh AN với BM . M Giải. (h.29) Hình 29 a) Hai tia MA, MN đối nhau nên M nằm giữa A và N ; Ba điểm A, M , N cùng nằm trên một đường thẳng (1) . Hai tia NM , NB đối nhau nên điểm N nằm giữa M và N và ba điểm B, M , N cùng nằm trên cùng một đường thẳng. ( 2) Hai đường thẳng (1) và ( 2 ) có hai điểm chung là M và N nên chúng trùng nhau do đó bốn điểm A, B, M , N thẳng hàng. b) AN =AM + MN =+ a MN (1) BM = BN + MN = b + MN ( 2) Vì a < b nên từ ( 3) và ( 4 ) suy ra AN < BM . Nhận xét: Để chứng minh bốn điểm A, B, M , N thẳng hàng ta đã chứng minh bốn điểm này nằm trên hai đường thẳng rồi chứng minh hai đường thẳng đó trùng nhau do chúng có hai điểm chung. BÀI TẬP 47. Xem hình 30 rồi cho biết: a) Hình đó có mấy tia? C z b) Hình đó có mấy đoạn thẳng? c) Độ dài của đoạn thẳng AB là bao nhiêu biết O là trung điểm của AB và OB = a ? y x 48. Gọi O là một điểm của đoạn thẳng O AB = 4cm . Xác định vị trí điểm O để: A B a) Tổng AB + BO đạt giá trị nhỏ nhất; Hình 30 b) Tổng AB + BO = 2 BO ; c) Tổng AB + BO = 3BO . 49. Gọi M là trung điểm của đoạn thẳng AB và C là một điểm của đoạn thẳng đó. Cho biết AB = 6 ( cm ) và AC = a ( cm ) , ( 0 < a ≤ 6 ) . Tính khoảng cách CM . Liên hệ tài liệu word toán SĐT hoặc zalo: 039.373.2038 -15-
  17. NÂNG CAO VÀ PHÁT TRIỂN TOÁN 6 Website: tailieumontoan.com 50. Cho đoạn thẳng CD = 5cm . Trên đoạn thẳng này lấy hai điểm I và K sao cho CI = 1cm ; DK = 3cm . a) Điểm K có phải là trung điểm của đoạn thẳng CD không? b) Chứng tỏ rằng điểm I là trung điểm của đoạn thẳng CK . 51 * . Cho đoạn thẳng AB ; điểm O thuộc tia đối của tia AB . Gọi M , N thứ là trung điểm của OA, OB . a) Chứng tỏ rằng OA < OB . b) Trong ba điểm O, M , N điểm nào nằm giữa hai điểm còn lại ? c) Chứng tỏ rằng độ dài đoạn thẳng MN không phụ thuộc vào vị trí của điểm O ( O thuộc tia đối của tia AB ). Liên hệ tài liệu word toán SĐT hoặc zalo: 039.373.2038 -16-
  18. NÂNG CAO VÀ PHÁT TRIỂN TOÁN 6 Website: tailieumontoan.com Chương II. GÓC § 1. Nửa mặt phẳng Kiến thức cơ bản 1. Hình gồm đường thẳng a và một phần mặt phẳng bị chia ra bởi a được gọi là một nửa mặt phẳng bờ a . Nhận xét: A Bất kì đường thẳng nào nằm trên mặt phẳng cũng là bờ chung của hai nửa mặt phẳng đối nhau. Trong hình 31 , nửa mặt phẳng bờ a chứa điểm A và a M nửa mặt phẳng bờ a chứa điểm M là hai nửa mặt phẳng Hình 31 đối nhau bờ a . 2. Tia Oz nằm giữa hai tia Ox và Oy nếu tia Oz cắt đoạn y B thẳng AB tại điểm M nằm giữa A và B z ( A ∈ Ox ; B ∈ Oy ; A và B khác 0 ) (xem hình 32 ). M Nhận xét: x Nếu hai tia Ox, O y đối nhau thì mọi tia Oz khác Ox, Oy đều O A nằm giữa hai tia Ox, Oy . Hình 32 Nâng cao: B Trên hình 33 : − Hai điểm A, B cùng thuộc một nửa mặt phẳng bờ a A thì đoạn thẳng AB không cắt a . − Hai điểm A và B thuộc hai nửa mặt phẳng đối nhau bờ a thì đoạn thẳng AC cắt a tại điểm nằm giữa A a và C . Thí dụ 13. Hình 33 C Cho tia Ot nằm giữa hai tia Oa, Ob không đối nhau; tia Om nằm giữa hai tia Oa, Ot ; tia On nằm giữa hai tia Ob, Ot . Giải thích vì sao tia Ot nằm giữa hai tia Om, On . Giải. (h. 34 ) Liên hệ tài liệu word toán SĐT hoặc zalo: 039.373.2038 -17-
  19. NÂNG CAO VÀ PHÁT TRIỂN TOÁN 6 Website: tailieumontoan.com Lấy điểm A trên tia Oa , điểm B trên tia O Ob ( A và B khác O ). Tia Ot nằm giữa hai tia Oa, Ob nên cắt đoạn thẳng AB tại điểm T nằm giữa A và B . Tương tự, tia Om cắt đoạn thẳng AT tại điểm M nằm B N giữa A và T ; tia On cắt đoạn thẳng BT A M T tại điểm N nằm giữa B và T . Từ đó suy b m ra T nằm giữa hai điểm M và N , do đó a t n tia Ot nằm giữa hai tia Om, On . Hình 34 Nhận xét . − Nếu hai tia Oa, Ob đối nhau thì kết luận trên vẫn đúng. − Thí dụ 13 cho ta một dấu hiệu nhận biết một tia nằm giữa hai tia khác. BÀI TẬP 52. Cho bốn điểm A, B, C , D không nằm trên đường thẳng a . Biết đoạn thẳng AB không cắt a , đoạn thẳng BC cắt a , đoạn thẳng CD không cắt a . Hỏi đoạn thẳng AD có cắt đường thẳng a không? 53. Năm bạn A, B, C , D, E có nhà ở hai bên đường cao tốc. A đến nhà B ; B đến nhà C ; C đến nhà D ; D đến nhà E đều phải đi qua đường cao tốc. Hỏi những bạn nào đến nhà nhau không đi qua đường cao tốc? 54. Cho đường thẳng m và năm điểm A, B, C , D, E không thuộc m . a) Chứng tỏ rằng trong hai nửa mặt phẳng đối nhau bờ là đường thẳng m , có một mặt phẳng chứa ít nhất 3 điểm. b) Cứ qua hai điểm vẽ một đoạn thẳng. Hỏi nhiều nhất có mấy đoạn thẳng cắt m ? 55. Trên hai nửa mặt phẳng đối nhau, bờ t ' t ta vẽ hai tia Ox và Oy ( O ∈ t ' t ) . Chứng tỏ rằng hoặc tia Ot hoặc tia Ot ' nằm giữa hai tia Ox và Oy . 56. Trên một nửa mặt phẳng bờ a lấy điểm A , trên nửa mặt phẳng đối lấy hai điểm B và C ( A, B, C ∉ a ) . Gọi M và N thứ tự là giao điểm của AB và AC với đường thẳng a . a) Chứng tỏ rằng tia BN nằm giữa hai tia BA , BC ; tia CM nằm giữa hai tia CA, CB . b) Giải thích tại sao hai đoạn thẳng BN và CM cắt nhau. Liên hệ tài liệu word toán SĐT hoặc zalo: 039.373.2038 -18-
  20. NÂNG CAO VÀ PHÁT TRIỂN TOÁN 6 Website: tailieumontoan.com §2. Góc. Số đo góc. Cộng số đo hai góc Kiến thức cơ bản: 1. Góc là hình gồm hai tia chung gốc (h.35a) Góc bẹt là góc có hai cạnh là hai tia đối nhau (h.35b) y x O y O x Hình 35a Hình 35b 2. Mỗi góc có một số đo dương. Số đo của góc bẹt là 180° . Sô đo của mỗi góc không vượt quá 180° . 3.   ⇔ A và B A= B  có cùng số đo A < B  ⇔ số đo A < số đo B   ⇔ số đo A > số đo B A > B  4. 0° < góc nhọn < góc vuông < góc tù < góc bẹt. ( 90° ) (180° ) z 5. Hai góc kề nhau là hai góc có một cạnh chung và y hai cạnh còn lại nằm trên hai nửa mặt phẳng đối nhau có bờ là cạnh chung.  ⇔ 6. A phụ với B A+ B  = 90° O x ⇔ A bù với B  = 180° A+ B Hình 36 Hai góc vừa kề, vừa bù gọi là hai góc kề bù. Hai góc kề bù có tổng bằng 180° và hai cạnh ngoài là hai tia đối nhau. + 7. Nếu tia Oy nằm giữa hai tia Ox và Oz thì xOy . yOz = xOz + Ngược lại nếu xOy  thì tia Oy nằm giữa hai tia Ox và Oz. (h.36) yOz = xOz Nâng cao: 1. Mệnh đề sau tương đương với tính chất trên: Liên hệ tài liệu word toán SĐT hoặc zalo: 039.373.2038 -19-
ADSENSE

CÓ THỂ BẠN MUỐN DOWNLOAD

THÔNG TIN
TRỢ GIÚP
HỖ TRỢ KHÁCH HÀNG
Theo dõi chúng tôi

Chịu trách nhiệm nội dung:

Nguyễn Công Hà - Giám đốc Công ty TNHH TÀI LIỆU TRỰC TUYẾN VI NA

LIÊN HỆ

Địa chỉ: P402, 54A Nơ Trang Long, Phường 14, Q.Bình Thạnh, TP.HCM

Hotline: 093 303 0098

Email: support@tailieu.vn

Giấy phép Mạng Xã Hội số: 670/GP-BTTTT cấp ngày 30/11/2015 Copyright © 2022-2032 TaiLieu.VN. All rights reserved.

 

Đồng bộ tài khoản
2=>2