Chuyên đề : PHƯƠNG TRÌNH ĐƯỜNG THẲNG VÀ ĐƯỜNG TRÒN
Daukhacha.toan@gmail.com
- Trang 1 -
79 BÀI TẬP HÌNH HỌC PHẲNG TIÊU BIỂU
- Tài liệu để ôn thi đại học và cao đẳng
- Tài liệu chỉ dùng cho HS học theo chương trình chuẩn
- Tài liệu gồm 79 bài tập được chọn lọc kĩ và giải chi tiết
BT1. Trong mặt phẳng
Oxy
cho các điểm
(
)
(
)
(
)
(
)
1;0 , 2;4 , 1;4 , 3;5
A B C D
− −
và đường thẳng
: 3 5 0
d x y
− − =
. Tìm điểm
trên d sao cho hai tam giác
,
MAB MCD
có diện tích bằng nhau.
Giải
M thuộc d thì
(
)
;3 5
M a a
−
Mặt khác :
(
)
3;4 5
1
: 4 3 4 0
3 4
AB AB
x y
AB x y
= − ⇒=
−
= ⇔ + − =
−
(
)
4;1 17
1 4
: 4 17 0
4 1
CD CD
x y
CD x y
=⇒=
+ −
= ⇔ − − =
Tính :
( )
(
)
(
)
1 2
4 3 3 5 4 4 3 5 17
13 19 3 11
, ,
5 5
17 17
a a a a
a a
h M AB h
+ − − − − −
− −
= = = = =
Nếu diện tich 2 tam giác bằng nhau thì :
1 2
11
13 19 3 11
5.13 19 17. 3 11
1 1
. .
12
13 19 11 3
2 2 5 17
8
a a
a a a
AB h CD h a a a
− = −
− −
=
= ⇔ = ⇔ ⇔
− = −
=
Vậy trên d có 2 điểm :
( )
1 2
11 27
; , 8;19
12 12
M M
−
BT2. Cho hình tam giác ABC có diện tích bằng 2. Biết
(
)
(
)
1;0 , 0;2
A B
và trung điểm I của AC
nằm trên đường thẳng
:
d y x
=
. Tìm toạ độ đỉnh C
Giải
Nếu C nằm trên
:
d y x
=
thì
(
)
A a;a
do đó suy ra
(
)
C 2a 1;2a
−
Ta có :
( )
0 2
, 2
2
d B d −
= = .
Theo giả thiết :
( ) ( ) ( )
2 2
1 4
. , 2 2 2 2 0
22
S AC d B d AC a a= =
⇒
= = − + −
2 2
1 3
2
8 8 8 4 2 2 1 0
1 3
2
a
a a a a
a
−
=
⇔ = − + ⇔ − − = ⇔ +
=
Vậy ta có 2 điểm C : 1 2
1 3 1 3 1 3 1 3
; , ;
2 2 2 2
C C
− − + +
 Trong mÆt ph¼ng täa ®é  cho tam gi¸c  víi
(
)
(
)
1;1 , 2;5
A B
−
và ®Ønh n»m trªn
www.MATHVN.com
www.MATHVN.com
Chuyên đề : PHƯƠNG TRÌNH ĐƯỜNG THẲNG VÀ ĐƯỜNG TRÒN
Daukhacha.toan@gmail.com - Trang 2 -
®−êng th¼ng
4 0
x
− =
, v träng t©m cña tam gi¸c n»m trªn ®−êng th¼ng
2 3 6 0
x y
− + =
. TÝnh
diÖn tÝch tam gi¸c 
Giải
Tọa độ C có dạng :
(
)
C 4;a
,
( ) ( )
5
3;4 1 1
: 4 3 7 0
3 4
AB
AB x y
AB x y
=
= − ⇒− −
= ⇔ + − =
−
Theo tính chất trọng tâm ;
1 2 4 1
3 3
1 5 6
3 3
3
A B C
G G
ABC
G
G
xxx
x x
y y y a a
y
y
+ + − +
= = =
⇔
+ + + + +
= =
=
Do G nằm trên
2 3 6 0
x y
− + =
, cho nên :
6
2.1 3 6 0 2
3
aa
+
⇒− + = ⇔ =
.
Vậy
(
)
M 4;2
và
( ) ( )
4.4 3.2 7
1 1 15
, 3 . , 5.3
2 2 2
16 9
ABC
d C AB S AB d C AB
+ −
= = ⇒= = =
+ (đvdt)
 Trong mÆt ph¼ng täa ®é
Oxy
cho tam gi¸c , víi
(2; 1) , (1; 2)
A B
− −
, träng t©m cña
tam gi¸c n»m trªn ®−êng th¼ng
: 2 0
d x y
+ − =
. T×m täa ®é ®Ønh C biÕt diÖn tÝch tam gi¸c 
b»ng
27
2

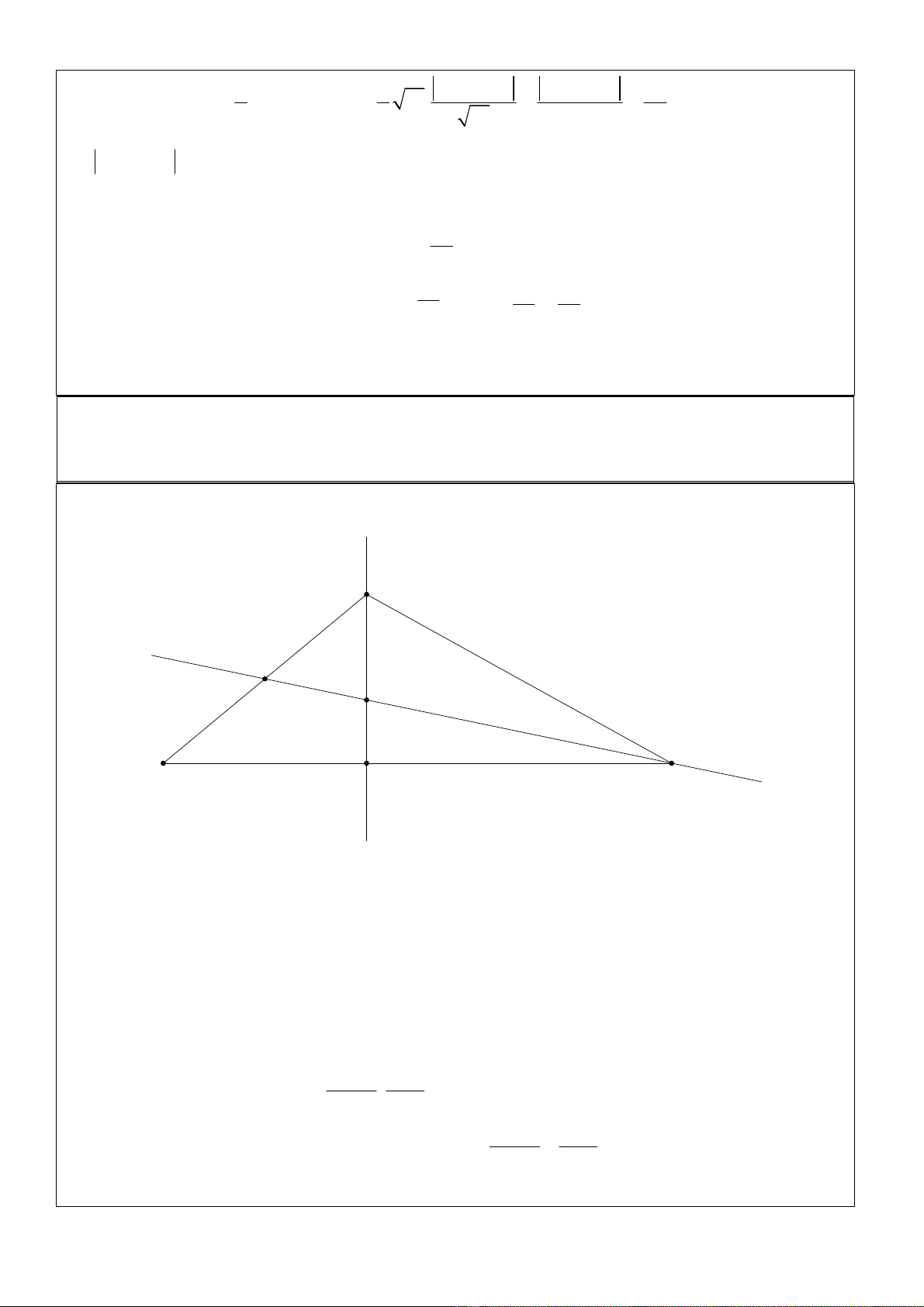
Giải.
d
M
A
B
C
Ta có : M là trung điểm của AB thì
3 1
;
2 2
M
−
. Gọi
(
)
C a;b
, theo tính chất trọng tam tam giác
:
3
3
3
3
G
G
a
x
b
y
+
=
−
=
Do G nằm trên d :
( )
3 3
2 0 6 1
3 3
a b a b
+ −
+ − = ⇔ + =
Ta có :
( ) ( ) ( )
3 5
2 1
1;3 : 3 5 0 ,
1 3
10
a b
x y
AB AB x y h C AB
− −
− −
=
⇒
= ⇔ − − = ⇔ =
www.MATHVN.com
www.MATHVN.com
Chuyên đề : PHƯƠNG TRÌNH ĐƯỜNG THẲNG VÀ ĐƯỜNG TRÒN
Daukhacha.toan@gmail.com - Trang 3 -
Từ giả thiết :
( )
2 5 2 5
1 1 27
. , 10.
2 2 2 2
10
ABC
a b a b
S AB h C AB − − − −
= = = =
2 5 27 2 32
2 5 27
2 5 27 2 22
a b a b
a b a b a b
− − = − =
⇔ − − = ⇔ ⇔
− − = − − = −
Kết hợp với (1) ta có 2 hệ :
( )
1 2
20
6 6 3
2 32 3 38 38 38 20
; , 6;12
33 3
6 6
12
2 22 3 18
6
b
a b a b
a b a aC C
a b a b
b
a b a
a
= −
+ = + =
− = =
=
⇔ ⇔ ⇔ ⇒− −
+ = + =
=
− = − = −
= −
BT5. Trong mặt phẳng Oxy cho
ABC
∆
có
(
)
A 2;1
. Đường cao qua đỉnh B có phương trình
3 7 0
x y
− − =
. Đường trung tuyến qua đỉnh C có phương trình
1 0
x y
+ + =
. Xác định tọa độ B
và C. Tính diện tích
ABC
∆
.
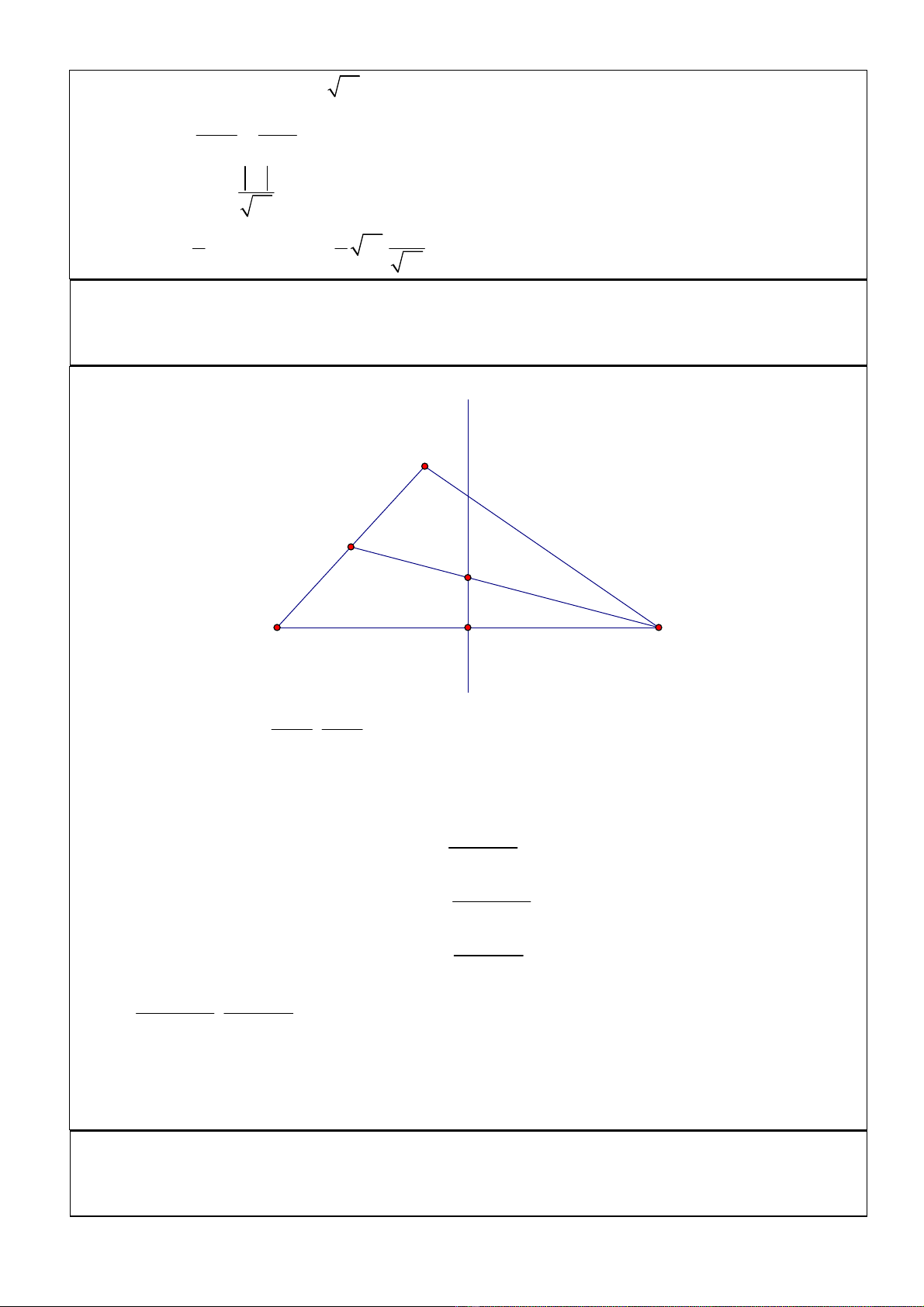
Giải
M
B
A
C
Đường thẳng AC qua
(
)
A 2;1
và vuông góc với đường cao kẻ qua B, nên có véc tơ chỉ phương
( ) ( ) ( )
2
1; 3 : 1 3
x t
n AC t R
y t
= +
= −
⇒
∈
= −
Tọa độ C là giao của (AC) với đường trung tuyến kẻ qua C :
2
1 3
1 0
x t
y t
x y
= +
⇒= −
+ + =
Giải ta được :
2
t
=
và
(
)
C 4; 5
−
. Vì B nằ
m trên
đườ
ng cao k
ẻ
qua B suy ra
(
)
3 7;
B a a
+
.
M là trung
đ
i
ể
m c
ủ
a AB
3 9 1
;
2 2
a a
M
+ +
⇒
.
M
ặ
t khác M n
ằ
m trên
đườ
ng trung tuy
ế
n k
ẻ
qua C :
( )
3 9 1
1 0 3
2 2
1; 2
a a a
B
+ +
+ + = ⇔ = −
⇒−
www.MATHVN.com
www.MATHVN.com
Chuyên đề : PHƯƠNG TRÌNH ĐƯỜNG THẲNG VÀ ĐƯỜNG TRÒN
Daukhacha.toan@gmail.com - Trang 4 -
Ta có :
(
)
( )
( )
1; 3 10
2 1
: 3 5 0
1 3
12
;10
AB AB
x y
AB x y
h C AB
= − − ⇒=
− −
= ⇔ − − =
=
Vậy :
( )
1 1 12
. , 10. 6
2 2 10
ABC
S AB h C AB
= = =
(đvdt).
BT6. Trong mặt phẳng với hệ tọa độ Oxy, cho tam giácABC biết
(
)
5;2
A
. Phương trình đường
trung trực cạnh BC, đường trung tuyến CC’ lần lượt là
– 6 0
x y
+ =
và
2 – 3 0
x y
+ =
. Tìm tọa
độ các đỉnh của tam giácABC
Giải
x
+
y
- 6 = 0
M
N
C
B
A
Gọi
(
)
B a;b
suy ra
5 2
;
2 2
a b
M
+ +
. M nằm trên trung tuyến nên :
2 14 0
a b
− + =
(1).
B, B đối xứng nhau qua đường trung trực cho nên
( ) ( )
:x a t
BC t R
y b t
= +
∈
= +
.
Từ đó suy ra tọa độ N :
6
2
3 6
2
6 0 6
2
a b
t
x a t a b
y b t x
x y
b a
y
− −
=
= +
− −
= + ⇒=
+ − =
+ −
=
3 6 6
;
2 2
a b b a
N
− − + −
⇔
. Cho nên ta có tọa độ
(
)
2 6;6
C a b a
− − −
Do C nằm trên đường trung tuyến
5 2 9 0
a b
− − =
(2)
Từ (1) và (2) :
( ) ( )
2 14 0 37
37;88 , 20; 31
5 2 9 0 88
a b a B C
a b b
− + = =
⇒⇔⇒− −
− − = =
BT7. Trong mặt phẳng với hệ tọa độ Oxy cho hai đường thẳng
: 3 8 0
x y
∆ + + =
,
':3 4 10 0
x y
∆ − + =
và điểm
(
)
2;1
A
−
. Viết phương trình đường tròn có tâm thuộc đường thẳng
∆
, đi qua điểm A và tiếp xúc với đường thẳng
∆
’.
www.MATHVN.com
www.MATHVN.com
Chuyên đề : PHƯƠNG TRÌNH ĐƯỜNG THẲNG VÀ ĐƯỜNG TRÒN
Daukhacha.toan@gmail.com - Trang 5 -
Giải
Gọi tâm đường tròn là I, do I thuộc
( )
2 3
: 2 3 ; 2
2
x t
I t t
y t
= − +
∆⇒− + − −
= − −
A thuộc đường tròn
( ) ( )
2 2
3 3
IA t t R
⇒= + + =
(1)
Đường tròn tiếp xúc với
(
)
(
)
3 2 3 4 2 10 13 12
'
5 5
t t t
R R
− + − − − + +
∆⇒= ⇔ =
. (2)
Từ (1) và (2) :
( ) ( ) ( ) ( ) ( )
2 2 2 2 2
13 12
3 3 25 3 3 13 12
5
t
t t t t t
+
+ + = ⇔ + + = +
BT8. Trong mặt phẳng với hệ tọa độ Oxy cho đường tròn hai đường tròn
2 2
( ) : – 2 – 2 1 0,
C x y x y
+ + =
2 2
( ') : 4 – 5 0
C x y x
+ + =
cùng đi qua
(
)
1;0
M
. Viết phương trình
đường thẳng qua M cắt hai đường tròn
( ), ( ')
C C
lần lượt tại A, B sao cho
2
MA MB
=
.
Giải
* Cách 1.
Gọi d là đường thẳng qua M có véc tơ chỉ phương
( )
1
; :
x at
u a b d
y bt
= +
=
⇒
=
Đường tròn
(
)
(
)
(
)
(
)
1 1 1 2 2 2
: 1;1 , 1. : 2;0 , 3
C I R C I R
= − =
, suy ra :
(
)
(
)
(
)
(
)
(
)
2 2 2 2
1 2
: 1 1 1, : 2 9
C x y C x y
− + − = + + =
Nếu d cắt
(
)
1
C
tại A :
( )
2
2 2 2
2 2 2 2
2 2
02 2
2 0 1 ;
2
t M ab b
a b t bt A
b
a b a b
ta b
= →
⇒+ − = ⇔ ⇒+
+ +
=
+
Nếu d cắt
(
)
2
C
tại B :
( )
2
2 2 2
2 2 2 2
2 2
06 6
6 0 1 ;
6
t M
a ab
a b t at B
a
a b a b
ta b
= →
⇒+ + = ⇔ ⇒− −
+ +
= −
+
Theo giả thiết :
(
)
2 2
2 4 *
MA MB MA MB= ⇔ =
.
Ta có :
2 2
2 2
2 2
2 2 2 2 2 2 2 2
2 2 6 6
4
ab b a ab
a b a b a b a b
+ = +
+ + + +
.
2 2
2 2
2 2 2 2
6 : 6 6 0
4 36
4. 36
6 : 6 6 0
b a d x y
b a b a b a d x y
a b a b
= − → + − =
⇔ = ⇔ = ⇔ = → − − =
+ +
* Cách 2.
- Sử dụng phép vị tự tâm I tỉ số vị tự
1
2
k
= −
. (Học sinh tự làm)
BT9. Trong mặt phẳng với hệ toạ độ Oxy, hãy viết phương trình các cạnh của tam giác ABC biết
trực tâm
(
)
1;0
H
, chân đường cao hạ từ đỉnh B là
(
)
0;2
K
, trung điểm cạnh AB là
(
)
3;1
M
.
Giải
www.MATHVN.com
www.MATHVN.com