7
CHƯƠNG 7: CHUYỂN ĐỘNG CƠ BẢN CỦA VẬT RẮN.
I. CHUYỂN ĐỘNG TỊNH TIẾN CỦA VẬT RẮN.
1. Định nghĩa và ví dụ.
a. Định nghĩa: Chuyển động tịnh tiến của vật rắn là
chuyển động mà mỗi đoạn thẳng thuộc vật đều song song
với vị trí ban đầu của nó.
b. Ví dụ:
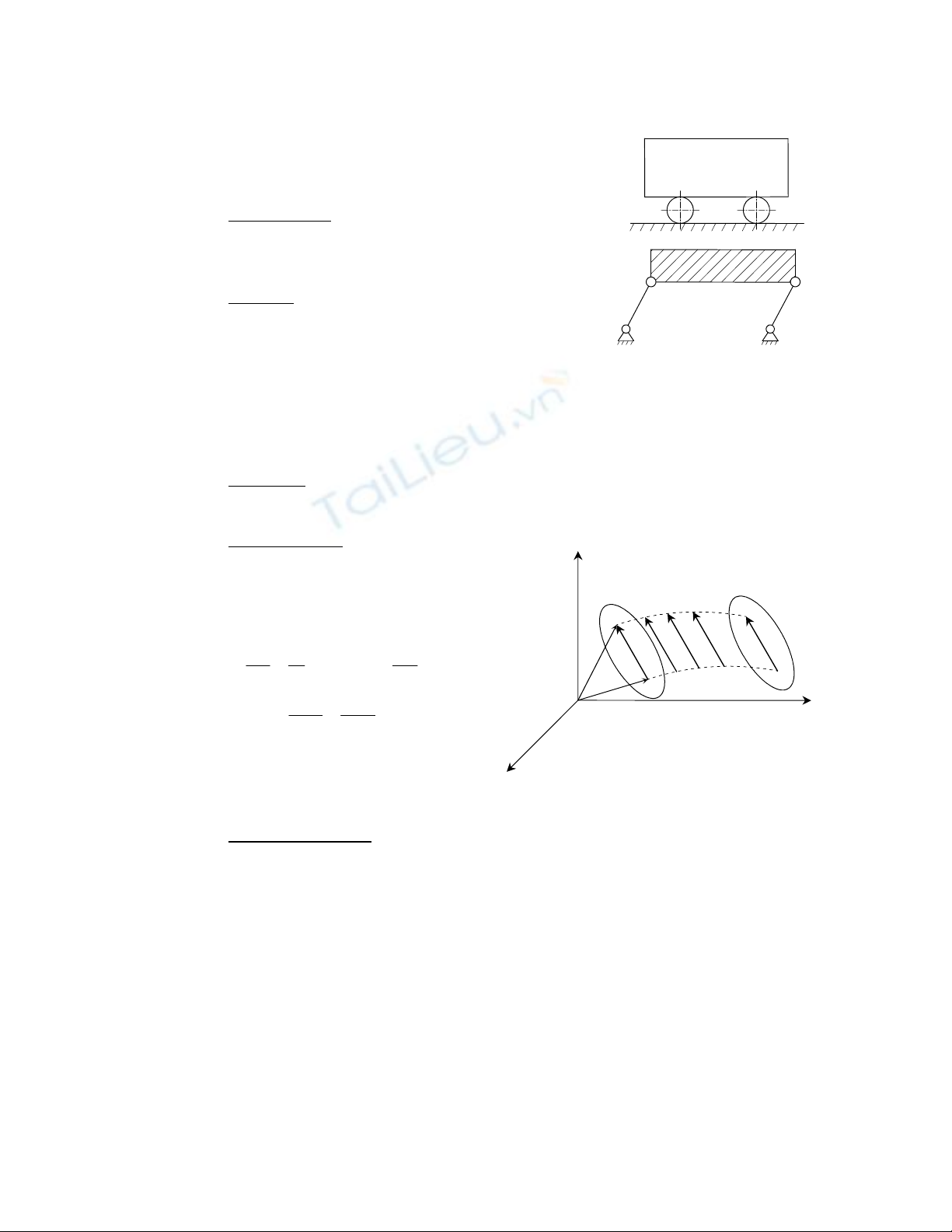
- Thùng xe chuyển động tịnh tiến so với mặt đường
trên đoạn đường thẳng.
- Chuyển động của khâu AB trong cơ cấu như hình vẽ.
Chuyển động tịnh tiến có thể là thẳng hoặc cong, các điểm thuộc vật rắn chuyển
động tịnh tiến có thể chuyển động không thẳng, không đều nên không có khái niệm điểm
chuyển động tịnh tiến.
2. Tính chất của chuyển động tịnh tiến.
a. Định lý: Trong chuyển động tịnh tiến, mọi điểm thuộc vật chuyển động giống hệt
nhau. Nghĩa là tại mỗi thời điểm vận tốc và gia tốc của các điểm thuộc vật giống hệt nhau.
Quỹ đạo của mọi điểm thuộc vật có thể tịnh tiến để trùng khít lên nhau.
b. Chứng minh: Trên vật khảo sát
lấy hai điểm A,B có các vectơ định vị
lần lượt là
A
r
r
,
B
r
r
. Ta có: BA
rrAB
=+
uuur
(7.1).
Do vật rắn chuyển động tịnh tiến
nên
AB
uuur
=const. Theo định nghĩa ta có:
(
)
BA
BA
A
drdrd
VrABV
dtdtdt
==+==
rr
uruuurur
r
BA
BA
dVdV
dtdt
WW
===
urur
uuruur
Nhìn vào (7.1) ta thấy quỹ đạo điểm
B chính là quỹ đạo điểm A trượt đi một
vectơ hằng
AB
uuur
.
c. Một số nhận xét:
- Khảo sát một số chuyển động tịnh tiến của vật rắn có thể thay bằng khảo sát
chuyển động của một điểm thuộc vật.
- Lấy tên chuyển động của chất điểm thuộc vật để đặt tên cho chuyển động của vật ấy.
- Lấy vận tốc, gia tốc của điểm thuộc vật làm vận tốc, gia tốc của vật.
II. CHUYỂN ĐỘNG CỦA VẬT RẮN QUANH TRỤC CỐ ĐỊNH.
1. Định nghĩa: Nếu trong quá trình chuyển động vật rắn có hai điểm cố định thì vật
rắn chuyển động quay quanh trục cố định đi qua hai điểm ấy.
Trục đi qua hai điểm cố định được gọi là trục quay của vật rắn.
A B
O
x
y
z
A
B
1
B
1
A
2
A
2
B
3
B
3
A
n
B
n
A
8
2. Phương trình chuyển động của vật rắn quay quanh trục cố
định .
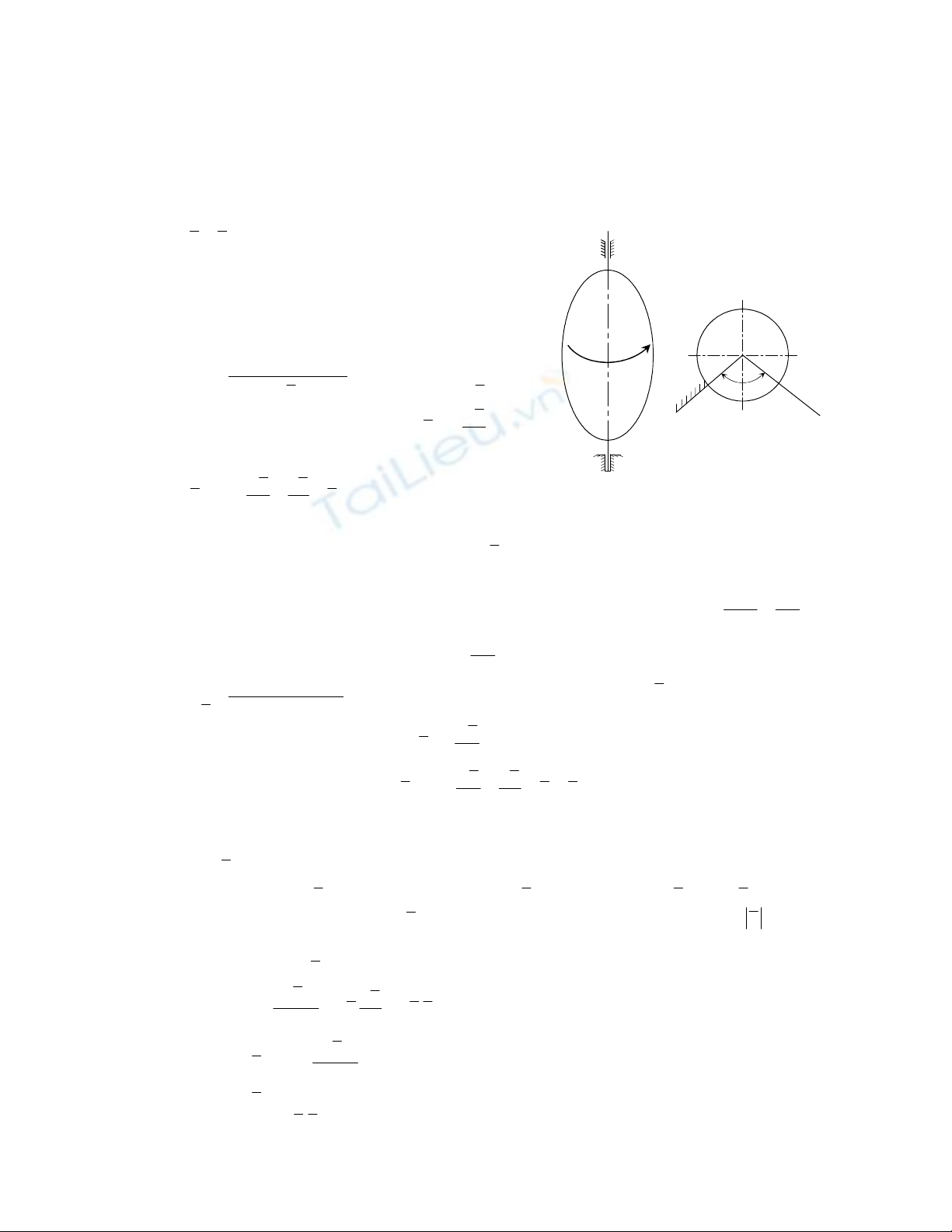
Dựng hai mặt phẳng
o
π
và
π
chứa trục quay của vật,
o
π
là mặt phẳng cố định còn
π
là
mặt phẳng động gắn với vật rắn. Vị trí của mặt phẳng
π
xác định vị trí của vật. Gọi ϕ là góc
giữa hai mặt phẳng
o
π
và
π
như vậy ϕ là thông số xác định vị trí của vật rắn quay quanh trục
cố định. Ta có phương trình chuyển động của vật rắn:
(
)
t
ϕ=ϕ
.
Quy ước:
0
ϕ>
khi vật quay ngược chiều kim
đồng hồ. Đơn vị tính góc ϕ là
[
]
rad
.
3. Vận tốc góc và gia tốc góc
của vật. :
a. Vận tốc góc: Giả sử trong khoảng thời gian
∆t góc định vị
ϕ
biến thiên một lượng là
∆ϕ
.
- Vận tốc góc trung bình: tb
t
∆ϕ
ω=
∆
.
- Vận tốc góc tức thời:
t0
d
lim
tdt
∆→
∆ϕϕ
ω===ϕ
∆
&
. (7.2)
Kết luận: Vận tốc góc của vật rắn quay quanh trục cố định là đạo hàm cấp một theo
thời gian góc quay của vật ấy. Đơn vị tính
ω
là
[
]
rad/s
.
Trong kỹ thuật ta hay dùng đơn vị vòng/phút, ký hiệu là n. Vậy trong một phút vật quay
được một góc
2.n
ϕ=π
rad. Do đó trong một giây vật quay được một góc
2.n.n
6030
ππ
ϕ==. Ta
có công thức chuyển đơn vị như sau.
.n
30
π
ω= rad/s .
b. Gia tốc góc: Giả sử trong khoảng thời gian ∆t vận tốc góc
ω
biến thiên một lượng là
∆ω
.
- Gia tốc góc trung bình: tb
t
∆ω
ε=
∆
.
- Gia tốc góc tức thời: t0
d
lim
tdt
∆→
∆ωω
ε===ω=ϕ
∆
&&&
. (7.3)
Kết luận: Gia tốc góc của vật rắn quay quanh trục cố định là đạo hàm cấp một theo
thời gian của vận tốc góc và bằng đạo hàm cấp hai theo thời gian góc quay vật ấy. Đơn vị
tính
ε
là
2
rad/s


.
Gia tốc góc
ε
đặc trung cho sự biến thiên
ω
theo thời gian. Khi
0
ε=
thì
const
ω=
, ta
có chuyển động quay đều. Khi
0
ε≠
ta có chuyển động quay biến đổi. Nếu
ω=ω
tăng dần
theo thời gian ta có chuyển động quay nhanh dần, ngược lại ta có chuyển động quay chậm dần.
Chú ý rằng
22
ω=ω
là đại lượng đặc trưng cho sự biến đổi vận tốc.
Ta có
(
)
2
dd
22.
dtdt
ωω
=ω=ωε
. Từ đó suy ra một số trường hợp sau:
-
(
)
2
d
00
dt
ω
ε=⇒=
⇒ Chuyển động quay đều.
-
0
ε≠
⇒ Chuyển động quay biến đổi.
•
.0
ωε>
⇒ Chuyển động quay nhanh dần.
ϕ
0
π
π
9
•
.0
ωε<
⇒ Chuyển động quay chậm dần.
4. Một số chuyển động quay đặc biệt.
a. Chuyển động quay đều: Chuyển động quay đều là chuyển động quay có
0
const
ω=ω=
.
Ta có: d
d.dt
dt
ϕ
ω=⇒ϕ=ω
. Tích phân hai vế ta có :
0
t
ϕ=ω+ϕ
(7.4)
0
d
d
0
dtdt
ω
ω
ε===
(Vì 0
const
ω=ω=
)
b. Chuyển động quay biến đổi đều: Chuyển động quay biến đổi đều là chuyển động
quay có
const
ε=
.
Ta có:
d
d.dt
dt
d
d.dt
dt
ω
ε=⇒ω=ε
ϕ
ω=⇒ϕ=ω
. Tích phân hai vế ta có : 0
2
00
t
tt
2
ω=ε+ω
ϕ=ε+ω+ϕ
(7.5)
5. Vectơ vận tốc góc và vectơ gia tốc góc.
Để biểu diễn rõ ràng những đặc trưng của chuyển động quay người
ta dùng khái niệm vectơ vận tốc góc và vectơ gia tốc góc.
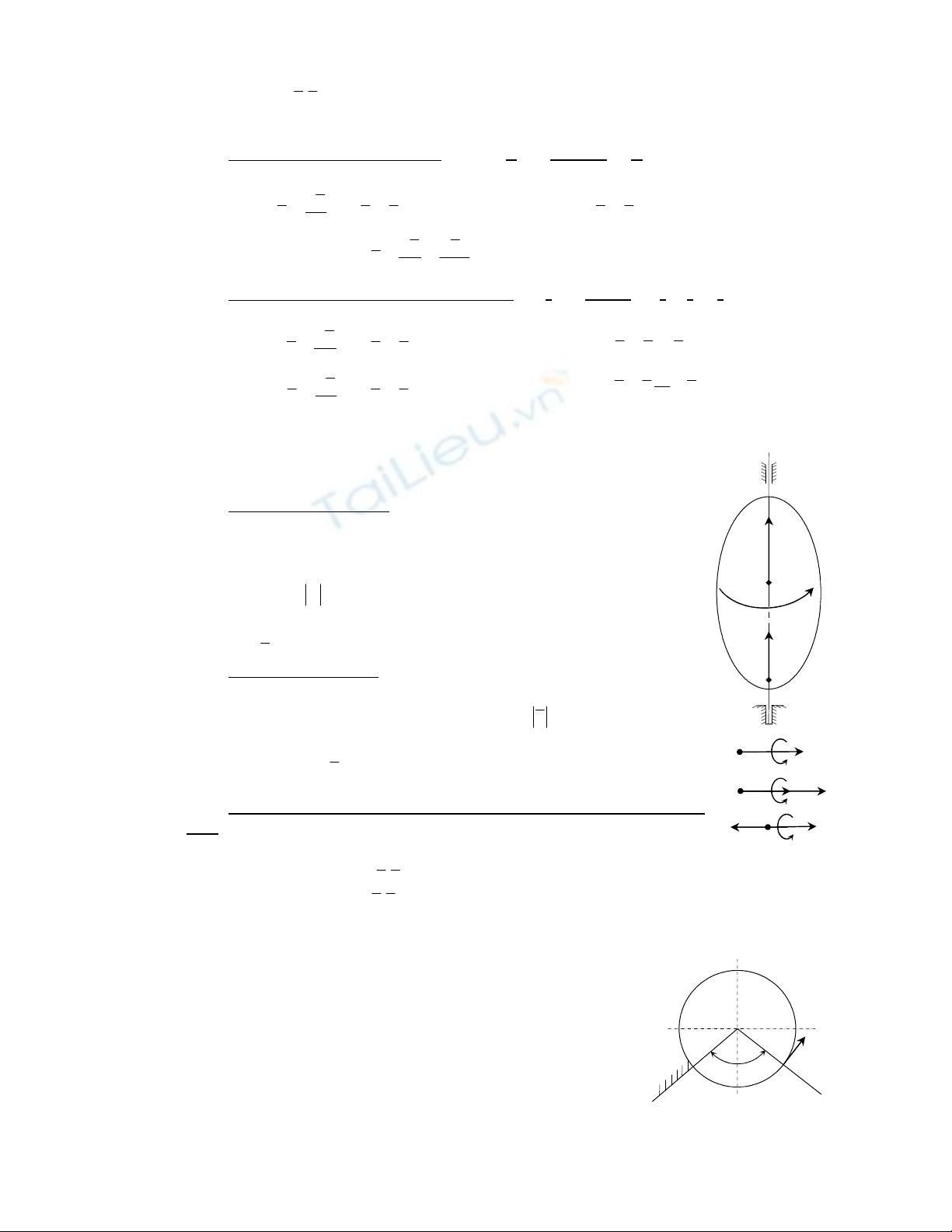
a. Vectơ vận tốc góc : Ký hiệu là
ω
r
, được xác định như sau:
- Phương
ω
r
trùng với trục quay của vật rắn.
- Chiều xác định sao cho nhìn từ mút
ω
r
thấy vật quay ngược
chiều kim đồng hồ.
- Độ lớn
ω=ω
r
.
Nếu gọi
k
r
là vectơ đơn vị trên trục quay ta có:
.k
ω=ω
r
r
.
b. Vectơ gia tốc góc: Ký hiệu là
ε
r
, được xác định như sau:
- Phương
ε
r
trùng với trục quay của vật rắn.
- Chiều xác phụ thuộc vào giá trị của
ε=ε
, nếu
0
ε>
thì
ε
r
cùng
phương với
ω
r
và ngược lại.
- Độ lớn
.k
ε=ε
r
r
.
c. Biểu diễn tính chuyển động theo vectơ vận tốc góc và gia tốc
góc:
- Quay đều:
const0
ω=⇒ε=
rr
- Quay nhanh dần:
.0
ωε>
⇒
ω
r
và
ε
r
cùng chiều.
- Quay chậm dần:
.0
ωε<
⇒
ω
r
và
ε
r
ngược chiều.
III. CHUYỂN ĐỘNG CỦA ĐIỂM THUỘC VẬT RẮN
QUANH TRỤC CỐ ĐỊNH.
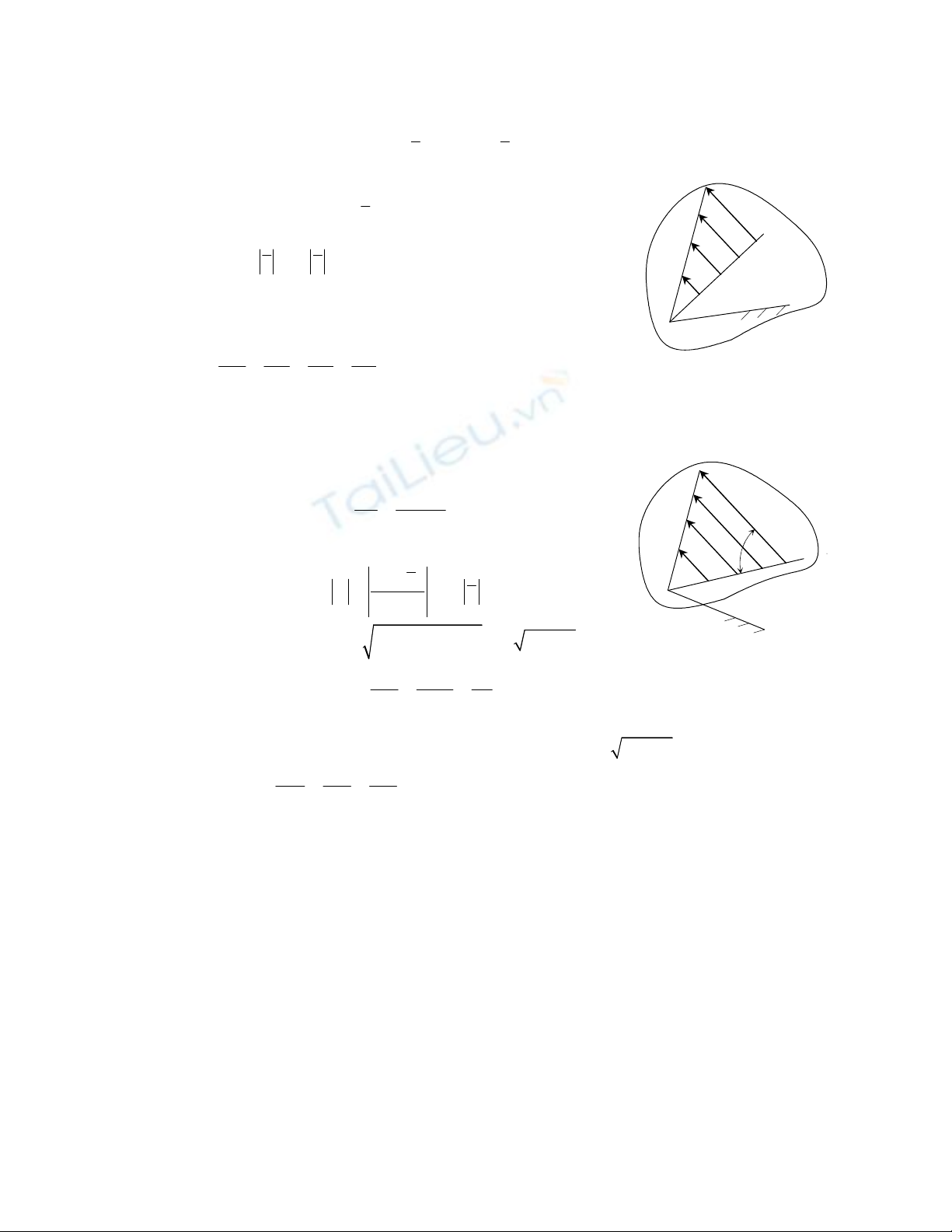
Xét chuyển động của điểm M thuộc vật rắn. M cách trục
quay z là R=IM. Khi vật rắn quay, quỹ đạo M là đường tròn tâm
I bán kính R=IM.
1. Phương trình chuyển động của điểm
thuộc vật.
Do đã biết quỹ đạo của M nên ta dùng hệ tọa độ tự nhiên
để khảo sát. Chọn O là giao điểm của quỹ đạo điểm M với mặt phẳng
0
π
làm gốc toạ độ,
ω
r
ε
r
0
ε>
ω
r
ε
r
ω
r
ω
r
ε
r
ϕ
I
0
π
π
M
10
chọn chiều quay ngựơc chiều kim đồng hồ làm chiều dương. Như vậy vị trí của M được
xác định bằng cung
¼
sOM
=. Ta có phương trình chuyển động của M:
¼
()
sOMR.t
==ϕ . (7.6)
2.Vận tốc của điểm thuộc vật.
Ta có:
t00
VVts.t
==
ur
rr
&
. Như vậy vận tốc điểm M vuông
góc với IM, hướng theo chiều quay của vật và có độ lớn
bằng:
VsR.R.
==ϕ=ω
&&
(7.7)
Nhận xét: Tại mỗi thời điểm xác định, vận tốc các điểm
thuộc vật rắn quay quanh trục cố định phân bố theo quy luật
tam giác vuông đồng dạng với hệ số đồng dạng là
MNAB
VVVV
IMINIAIB
ω====
urururur
.
3.Gia tốc của điểm thuộc vật.
Điểm M chuyển động tròn nên trong trường hợp tổng quát ta có:
n
WWW
τ
=+
uuruuruur
.
-
n
W
uur
hướng vào tâm quỹ đạo.
()
2
2
n2
R.
V
R..
R
ω
===ω
ρ
W
-
τ
uur
W
hướng tiếp tuyến quỹ đạo.
(
)
dR.
VR.R..
dt
τω
===ω=ε
&&
W
Gia tốc toàn phần
()()
22
n42
n22
WWWR
WR.
tg WR.
τ
τ
=+=ω+ε
εε
α===
ωω
(7.8)
Nhận xét: Gia tốc của các điểm thuộc vật rắn quay quanh trục cố định phân bố theo
quy luật tam giác thường đồng dạng với hệ số đồng dạng là
42
ω+ε
.
Ta có: N
MA
W
WW
IMINIA
==.
IV. MỘT SỐ TRUYỀN ĐỘNG CƠ BẢN.
1. Khái niệm về truyền động.
Trong các cơ cấu máy thường gồm ba bộ phận là bộ phận sinh năng lượng, bộ phận
truyền năng lượng (truyền động) và bộ phận công tác. Ví dụ trong hệ động lực tàu bộ phận
sinh năng lượng là động cơ, bộ phận truyền động là hệ trục còn bộ phận công tác là chân
vịt.
Chúng ta thường gặp một số dạng truyền động sau:
- Truyền động điện: cự ly truyền động rất xa.
- Truyền động thuỷ lực: cự ly truyền động trung bình.
- Truyền động cơ khí: cự ly truyền động ngắn.
Trong môn học này chúng ta chỉ nghiên cứu truyền động cơ khí.
M
N
A
B
I
π
0
π
M
V
ur
N
V
ur
A
V
ur
B
V
ur
π
0
π
M
N
A
B
I
M
W
uur
N
W
uur
A
W
uur
B
W
uur
α
11
2. Truyền động chuyển động quay thành chuyển động quay.
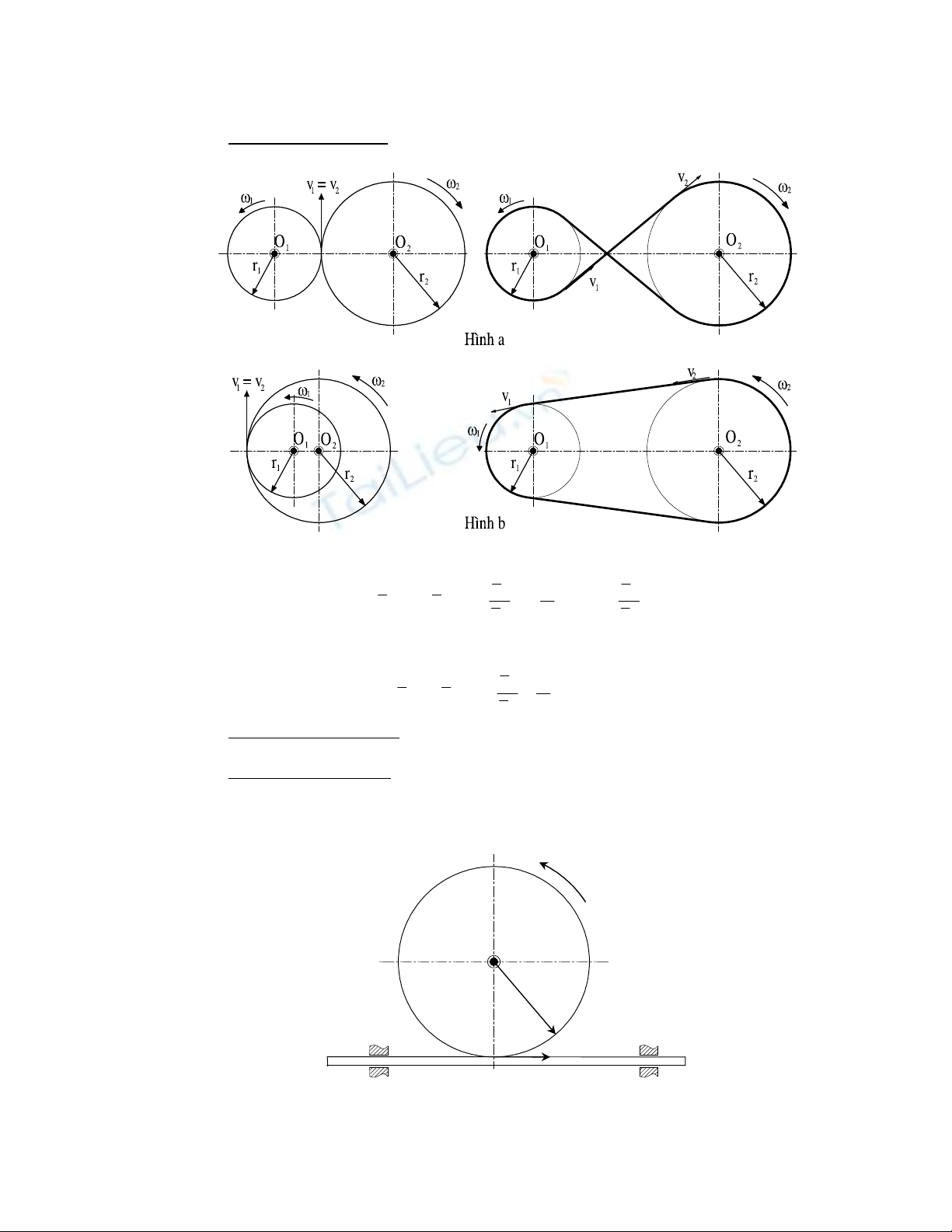
a. Hai trục song song :
- Truyền động bánh răng trụ ăn khớp ngoài, bánh ma sát ngoài, bộ truyền đai chéo:
Ta có
12
VV
=
urur
nên
ω=−ω
1122
rr
⇔
12
21
r
r
ω
=−
ω. Tỷ số
1
2
ω
ω
được gọi là tỷ số truyền,
dấu trừ chứng tỏ chúng quay ngược chiều nhau.
- Truyền động bánh răng trụ ăn khớp trong, bánh ma sát trong, bộ truyền đai thẳng:
Tương tự
12
VV
=
urur
nên
1122
rr
ω=ω
⇔
12
21
r
r
ω
=
ω.
b. Hai trục vuông góc : Truyền động bánh răng côn, bánh ma sát côn, trục vít bánh
vít. c. Hai trục chéo nhau : Cơ cấu cácđăng.
3. Truyền động chuyển động quay thành chuyển động tịnh tiến
và ngược lại.
- Truyền động bánh răng, thanh răng và truyền động bánh ma sát.
Ta có
12
VV
=
urur
⇒
Vr.
=ω
- Truyền động bằng cơ cấu cam.
1
O
12
VV
=
1
r