1
PHẦN 2: ĐỘNG HỌC
MỞ ĐẦU
Động học khảo sát chuyển động cơ học của vật thể (chất điểm) về mặt hình học,
không quan tâm đến nguyên nhân gây chuyển động và biến đổi chuyển động của chúng.
Khi vật thể có kích thước rất bé so với quỹ đạo chuyển động của nó hoặc có thể
bỏ qua thì ta coi đó là chất điểm chuyển động, gọi tắt là động điểm.
Để đơn giản chúng ta xem không gian và thời gian không phụ thuộc vào chuyển
động của vật khảo sát và gọi là không gian thuyệt đối và thời gian tuyệt đối. Không gian
tuyệt đối được quan niệm là không gian Ơcơlít không phụ thuộc vào thời gian và các vật
thể chuyển động quanh nó. Thời gian tuyệt đối được quan niệm là thời gian trôi đều từ quá
khứ qua hiện tại đến tương lai.
Chuyển động xảy ra trong không gian nhưng hoàn toàn có tính tương đối phụ
thuộc vào vật lấy làm mốc để theo dõi chuyển động. Vật lấy làm mốc được gọi là hệ quy
chiếu.
Để tính thời gian ta chọn một thời điểm tuỳ ý làm thời điểm gốc (t0), thường chọn
t0 là lúc bắt đầu khảo sát chuyển động.
Động học được chia làm hai phần chính là “Động học điểm” và “Động học vật
rắn”. Nghiên cứu động học điểm ngoài ý nghĩa tự thân nó còn nhằm chuẩn bị cho khảo sát
chuyển động của vật rắn.
Động học nghiên cứu 3 vấn đề chính:
1. Phương trình chuyển động → Xác định vị trí đối tượng.
2. Vận tốc chuyển động → Xác định hướng và tốc độ chuyển động.
3. Gia tốc chuyển động → Biểu thị sự thay đổi vận tốc.
CHƯƠNG 6: ĐỘNG HỌC ĐIỂM
I. NGHIÊN CỨU CHUYỂN ĐỘNG CỦA ĐIỂM BẰNG PHƯƠNG PHÁP VECTƠ.
1. Phương trình chuyển động của điểm.
Xét điểm M chuyển động trong hệ quy chiếu Oxyz. Vị trí của
điểm M được xác định bởi vectơ
r
r
=
OM
uuuur
. M chuyển động thì
r
r
thay
đổi theo thời gian.
(
)
=
rr
(6.1)
Phương trình (6.1) được gọi là phương trình chuyển động của
điểm M dạng vectơ. M chuyển động liên tục, tại mỗi thời điểm M có
một vị trí xác định và có hướng chuyển động xác định nên
(
)
rt
r
là
hàm liên tục, đơn trị.
Tập hợp các vị trí của M trong hệ quy chiếu Oxyz được gọi là quỹ đạo điểm M
trong hệ quy chiếu ấy. Phương trình (6.1) được gọi là phương trình tham số của quỹ đạo.
• Nếu quỹ đạo là đường thẳng ⇒ Chất điểm chuyển động thẳng.
• Nếu quỹ đạo là đường cong ⇒ Chất điểm chuyển động cong.
2. Vận tốc điểm.
Xét chất điểm M chuyển động trên quỹ đạo C như hình vẽ.
Giả sử tại thời điểm t chất điểm tại vị trí M, xác định bởi vectơ
r
r
.
Tại thời điểm 1
ttt
=+∆
chất điểm tại vị trí M1, xác định bởi vectơ
1
r
r
.
O
x
y
z M
O
M
1
M
r
r
1
r
r
V
ur
tb
V
ur
r
∆
r
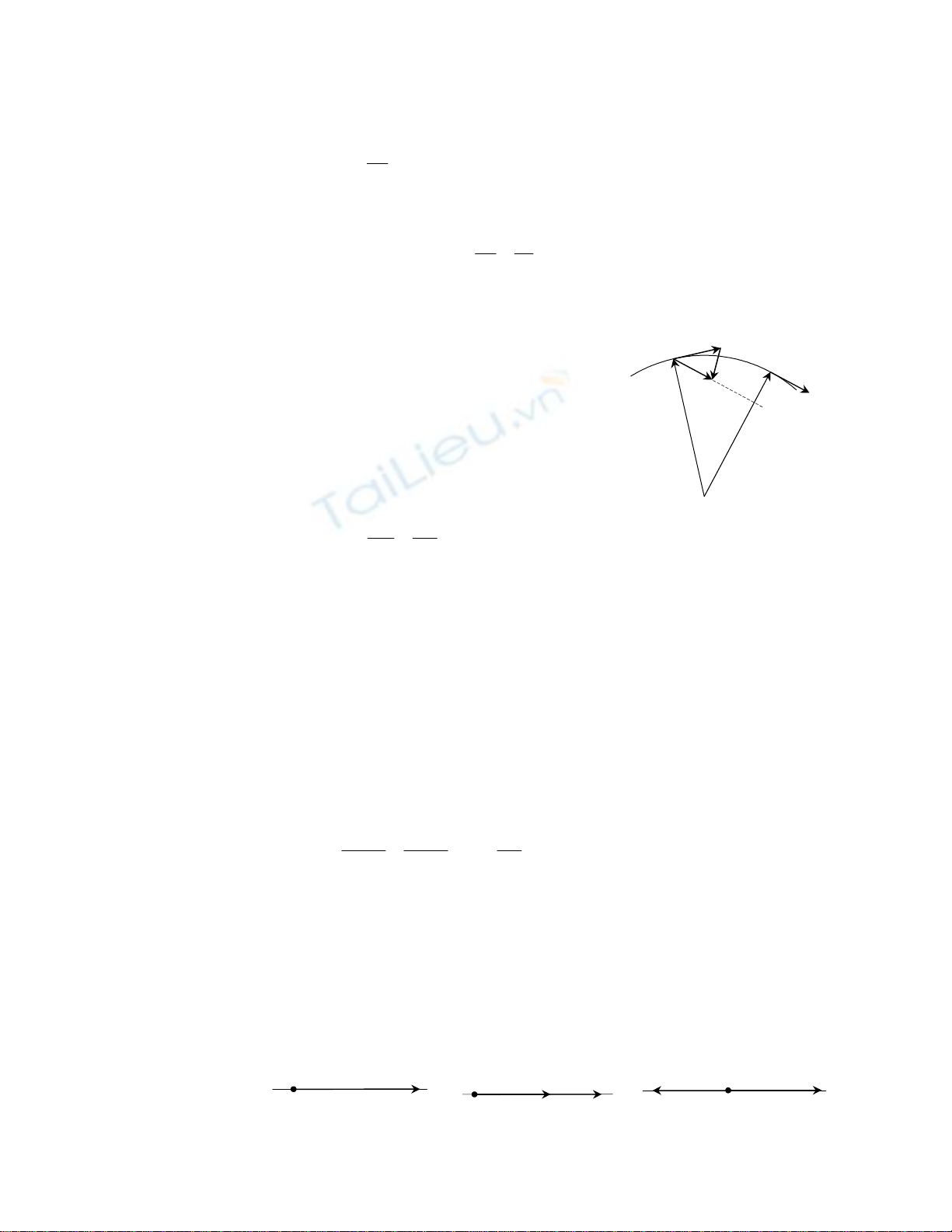
2
Sau một khoảng thời gian
1
ttt
∆=−
chất điểm di chuyển được một đoạn là
1
MM
uuuuur
=
1
r
r
-
r
r
=
r
∆
r
.
Đại lượng tb
r
V
t
∆
=
∆
r
ur
được gọi là vận tốc trung bình của điểm trong khoảng thời gian
∆t,
tb
V
ur
hướng theo cát tuyến MM1.
Vận tốc tức thời của động điểm tại thời điểm t được xác định như sau:
V
ur
=tb
t0t0
rdr
limVlimr
tdt
∆→∆→
∆
===
∆
rr
ur
r
&
(6.2)
Khi ∆t→ 0 ⇒ M1→ M ⇒
V
ur
nằm theo phương tiếp tuyến với quỹ đạo tại M.
Kết luận: Vận tốc của điểm là đạo hàm bậc nhất theo thời gian của vectơ định vị
điểm ấy. Đơn vị đo vận tốc là mét/giây, ký hiệu là m/s.
3. Gia tốc điểm.
Giả sử: Tại thời điểm t, chất điểm tại M, vận tốc là
V
ur
.
Tại thời điểm t1
= t+∆t, chất điểm tại M1
, vận tốc là
1
V
ur
. Sau
một khoảng thời gian ∆t, vận tốc chất điểm biến thiên một
đại lượng
V
∆
ur
=
V
ur
-
1
V
ur
.
Gia tốc của điểm tại thời điểm t được xác định theo công
thức:
.
tb
t0t0
dV
limlimVr
tdt
V
WW
∆→∆→
∆
=====
∆
urur
uuruurur
r
&&
(6.3)
Kết luận: Gia tốc của điểm là đạo hàm bậc nhất theo thời gian của vectơ vận tốc và
là đạo hàm bậc hai theo thời gian của vectơ định vị điểm ấy.
V
∆
ur
luôn hướng về phía lõm
của quỹ đạo do vậy
W
uur
cũng luôn hướng về phía lõm quỹ đạo. Đơn vị đo gia tốc là
mét/giây2, ký hiệu là m/s2.
4. Một số nhận xét về tính chất chuyển động.
Xét tích V
W
∧
uruur
=
V
.
W
.sin(
V
ur
,
W
uur
).
V
W
∧
uruur
=0 ⇒ sin(
V,
W
uruur
)= 0 ⇒
V
ur
và
W
uur
cùng phương ⇒ Chuyển động thẳng.
V
W
∧
uruur
≠
0 ⇒ sin(
V,
W
uruur
)
≠
0 ⇒
V
ur
và
W
uur
không cùng phương ⇒ Chuyển động
cong.
Ta nhận thấy giá trị V2 cũng đặc trưng cho sự thay đổi vận tốc, và ta có:
2
V
=
(
)
2
V
ur
Xét đại lượng : 22
d(V)d(V)dV
2.V.2.V.
dtdtdt
W
===
urur
ururuur
, ta có
V.
W
uruur
=
V.
W
.cos(
V,
W
uruur
).
V.
W
uruur
=0 ⇒ cos(
V,
W
uruur
)= 0 ⇒
V
ur
và
W
uur
vuông góc hoặc
W
uur
= 0 ⇒ Chuyển động
đều.
V.
W
uruur
>0 ⇒ cos(
V,
W
uruur
) > 0 ⇒ (
V,
W
uruur
) < 90o ⇒ Chuyển động nhanh dần.
V.
W
uruur
<0 ⇒ cos(
V,
W
uruur
) < 0 ⇒ (
V,
W
uruur
) > 90o ⇒ Chuyển động chậm dần.
Tính chất chuyển động được tóm tắt trong bảng sau:
Chuyển
động Đều Nhanh dần Chậm dần
Thẳng
M
V
ur
V
ur
W
uur
M
M
W
uur
V
ur
O
M
1
M
1
V
ur
1
V
ur
V
ur
V
∆
ur
r
r
1
r
r
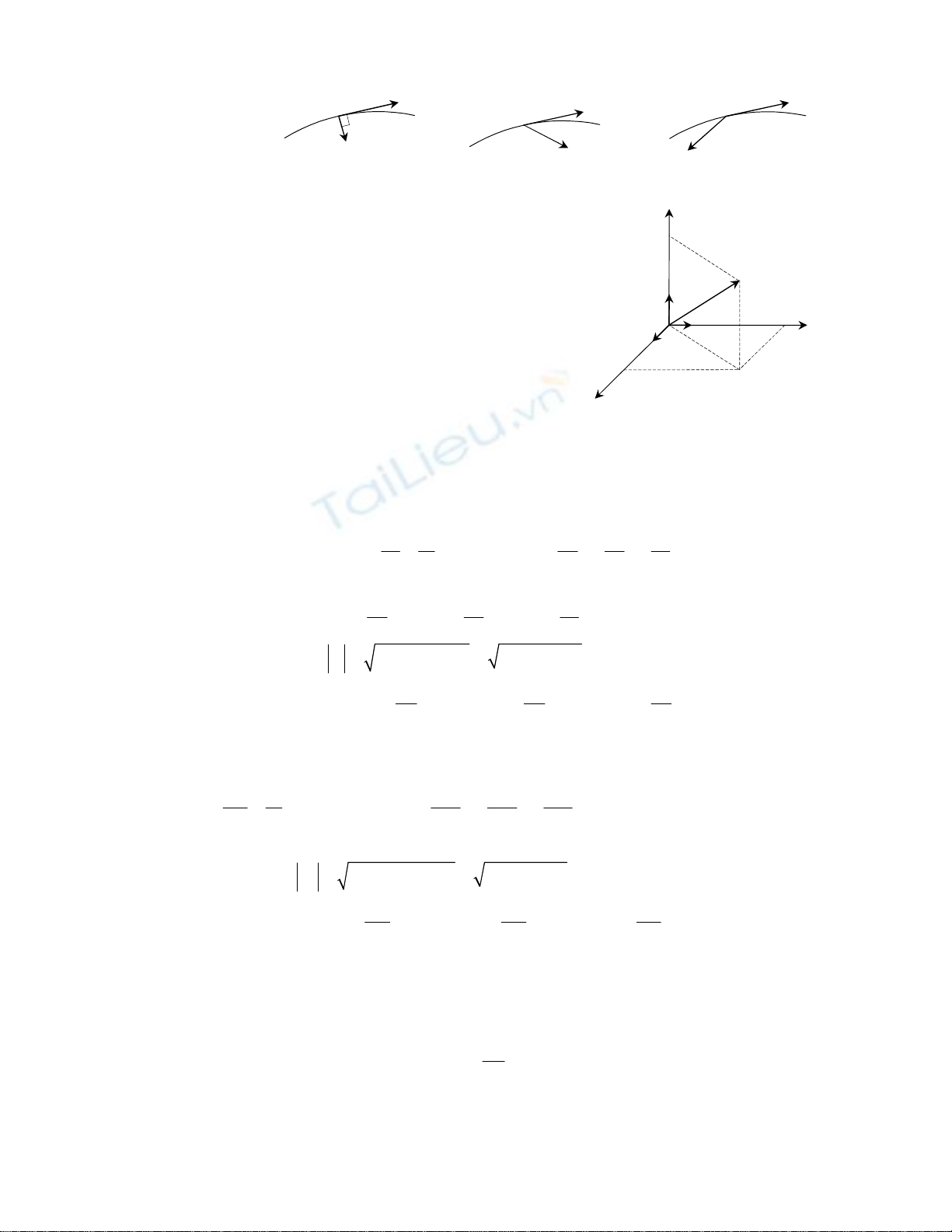
3
Cong
II. NGHIÊN CỨU CHUYỂN ĐỘNG CỦA ĐIỂM
BẰNG PHƯƠNG PHÁP ĐÊCÁC.
1. Phương trình chuyển động của
điểm.
Xét điểm M(x,y,z)
∈
Oxyz.
r
r
=
OM
uuuur
.
i
r
,j
r
,
k
r
là các vectơ đơn vị trên các trục
Ox,Oy,Oz.
Vị trí điểm M được xác định bằng vectơ định vị
r
r
.
r
r
= x.
i
r
+y. j
r
+z.
k
r
.
Khi M chuyển động thì: x=x(t), y=y(t), z=z(t) (6.4)
Đây là phương trình chuyển động của điểm M trong hệ tọa độ Đề các.
2. Vận tốc điểm.
Theo (6.2) ta có:
V
ur
=
()
drd
xiy.jz.k
dtdt
=++
r
rr
v
=
dxdydz
ijk
dtdtdt
++
rrr
.
Chiếu đẳng thức trên lên các trục tọa độ ta được:
xdx
Vx
dt
==
ur
&
;ydy
Vy
dt
==
ur
&
;zdz
Vz
dt
==
ur
&
(6.5)
⇒
222222
xyz
y
xz
VVVVVxyz
V
VV
Cos(Ox,V);Cos(Oy,V);Cos(Oz,V)
VVV
==++=++
===
ur
&&&
ururur (6.6)
3. Gia tốc điểm.
Theo (6.3) ta có:
W
uur
=
()
xyz
dVd
ViV.jV.k
dtdt
=++
ur
rr
v
=y
xz
dV
dVdV
ijk
dtdtdt
++
rrr
=
x.iy.jz.k
++
rrr
&&&&&&
Chiếu đẳng thức trên lên các trục tọa độ ta được:
x
W
uur
=
x
&
&
;
y
W
uur
=
y
&
&
;
z
W
uur
=
z
&
&
(6.7)
⇒
222222
xyz
y
xz
xyz
Cos(Ox,);Cos(Oy,);Cos(Oz,)
WWWWW
W
WW
WWW
WWW
==++=++
===
uur
&&&&&&
uuruuruur (6.8)
Ví dụ: Điểm M
∈
mặt phẳng Oxy có phương trình chuyển động:
xb.sint
yd.cost
=ω
=ω
(b,d là các hằng số dương, giả sử b<d)
Xác định: - Phương trình quỹ đạo điểm M.
- Vận tốc, gia tốc tại t1=
2
π
ω
.
Bài giải:
1. Tìm phương trình quỹ đạo điểm M. Khử tham số t ta có:
M
V
ur
W
uur
M
W
uur
V
ur
M
V
ur
W
uur
M
Z
Y
X
x
y
z
k
r
j
r
i
r
O
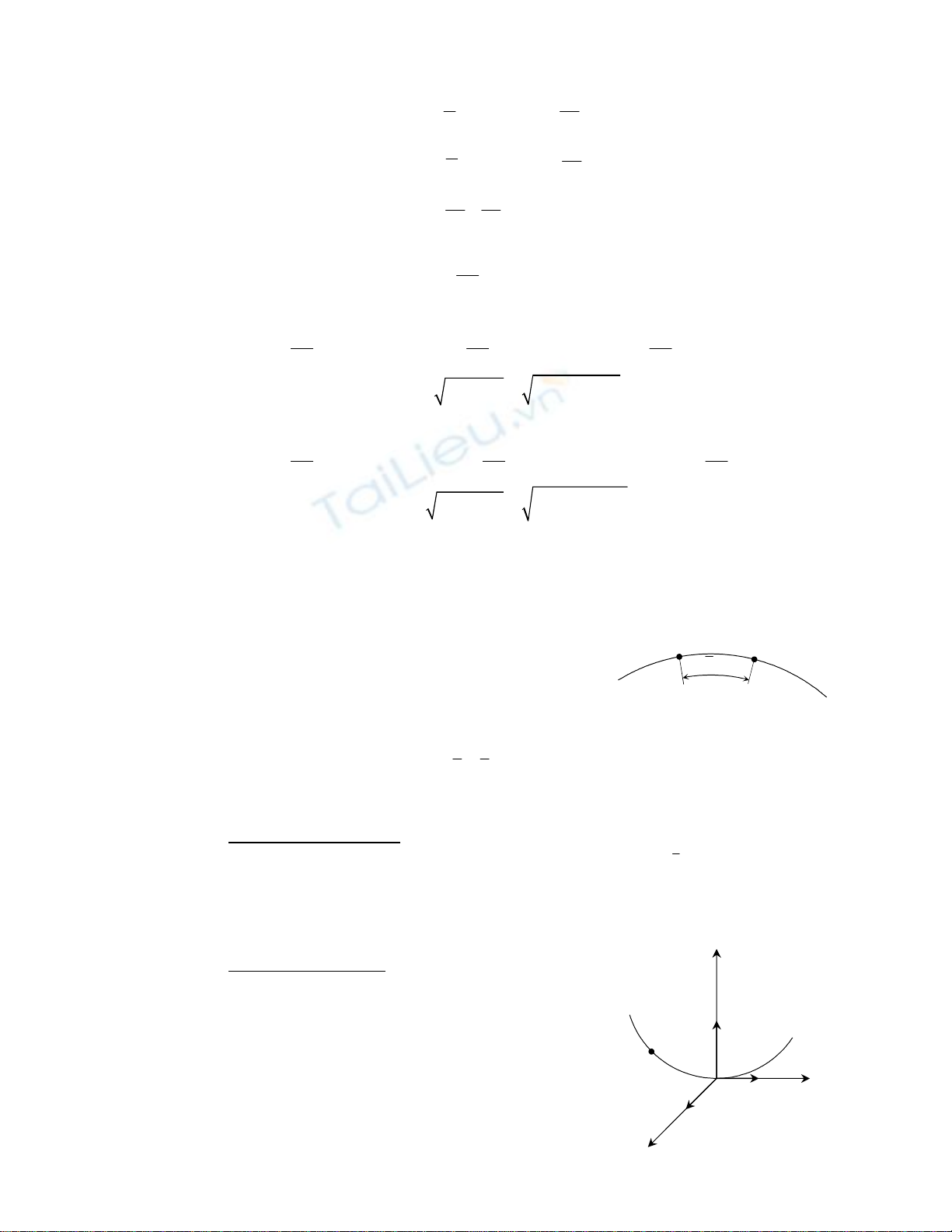
4
2
22
2
2
2
xx
(1)
sintsint
bb
yy
cost
(2)
cost
dd
ω=ω=

⇔


ω= ω=
(1)+ (2) ⇔
22
22
22
xy
sintcost
bd
ω+ω=+=1 ⇒ Phương trình quỹ đạo điểm M là đường
elíp có trục bé là 2b, trục lớn là 2d.
2. Tìm vận tốc, gia tốc tại t1=
2
π
ω
.
a, Tìm vận tốc: Ta có:
x
V
=
x
&
=b.ω.cos(ωt);
y
V
=
y
&
= -d.ω.sin(ωt).
Tại t1=
ω
π
2
ta có
x
V
=b.ω.cos(ω
ω
π
2
) = 0;
y
V
= -d.ω.sin(ω
ω
π
2
) = -d.ω.
()
2
222
xy
VVV0d.
=+=+−ω
= d.ω.
b, Tìm gia tốc: Ta có:
x
W
=
x
V
&
= -b.ω2.sin(ωt);
y
W
=
y
V
&
= -d.ω2.cos(ωt).
Tại t1=ω
π
2
ta có
x
W
= -b.ω2.sin(ωω
π
2
) = -b.ω2;
x
W
= -d.ω2.cos(ωω
π
2
) = 0.
()
2
2222
xy
b.0
WWW
=+=−ω+
= b.ω2.
III. NGHIÊN CỨU CHUYỂN ĐỘNG CỦA ĐIỂM BẰNG PP TọA Độ TỰ NHIÊN.
1. Phương trình chuyển động.
Phương pháp tọa độ tự nhiên được áp dụng khi biết trước quỹ đạo chuyển động
của chất điểm.
Giả sử chất điểm M chuyển động theo quỹ đạo (C)
cho trước trong một hệ quy chiếu không gian. Chọn điểm
O tuỳ ý trên quỹ đạo (O
∈
C) làm điểm gốc và định chiều
dương trên quỹ đạo.
Điểm M được xác định bằng độ dài đại số cung OM. Do M chuyển động nên:
ss(t)
=
(6.9)
2. Hệ tọa độ tự nhiên.
a, Mặt phẳng mật tiếp:
Lấy cung vô cùng bé MM1 trên quỹ đạo có giá trị đại số là
s
d
. Một cách gần đúng
có thể xem cung MM1 nằm trong một mặt phẳng π. Mặt phẳng π được gọi là mặt phẳng
mật tiếp của quỹđạo tại M.
Chú ý: Nếu quỹ đạo là đường cong phẳng thì mặt phẳng quỹ đạo cũng chính là mặt
phẳng mật tiếp mọi điểm trên quỹ đạo.
b, Hệ tọa độ tự nhiên: Trong mặt phẳng mật điểm M
của quỹ đạo dựng các trục:
Mt: Hướng theo tiếp tuyến quỹ đạo.
Mn: Hướng theo pháp tuyến quỹ đạo về phía lõm.
Mb: Vuông góc với mặt phẳng mật tiếp (chứa Mt và
Mn). Mtnb được gọi là hệ tọa độ tự nhiên, Mn gọi là pháp
tuyến chính của quỹ đạo, vectơ đơn vị trên trục này là
0
n
r
. Mb
0
- +
M t
b
n
0
n
r
0
t
r
0
b
r
O M
(
)
St
-
+
(C)
5
gọi là trùng pháp tuyến vectơ đơn vị trên trục này là 0
b
r
. Mt là tiếp tuyến có vectơ đơn vị là
0
t
r
. Người ta thường chọn 0
b
r
sao cho Mtnb tạo thành hệ trục thuận.
Tại mỗi thời điểm chất điểm có một vị trí M xác định và ta dựng được một hệ tọa độ tự
nhiên tương ứng. Hệ tọa độ tự nhiên thay đổi theo vị trí điểm M trên quỹ đạo phản ánh một
phần tính chất hình học của quỹ đạo.
3. Độ cong và bán kính cong quỹ đạo.
Nhận xét: Quỹ đạo càng cong thì tiếp tuyến của nó đổi hướng càng nhanh dọc
theo quỹ đạo ấy.
Người ta đưa ra khái niệm độ cong quỹ đạo trung
bình: tb
k
s
∆ϕ
=
∆
. tb
k
là độ cong trung bình của cung
MM1.
Độ cong quỹ đạo tại M được định nghĩa:
s0
d
klim
sds
∆→
∆ϕϕ
==
∆
Đại lương
1
k
ρ=
gọi là bán kính cong quỹ đạo tại điểm M.
Ví dụ: Xét đường tròn tâm O, bán kính R. Ta có ds = R.dϕ.
Vậy
dd1
k
dsR.dR
ϕϕ
===
ϕ mà
1
k
ρ=
nên ta luôn có
R
=
ρ
. Bán kính cong của đường
tròn tại mọi điểm đều bằng bán kính của đường tròn đó.
4. Vận tốc điểm.
Vì vectơ
V
ur
hướng theo tiếp tuyến quỹ đạo nên
t0
VV.t
=
ur
r
. Ta có:
drdrdsdr
V.s.
dtdsdtds
===
rrr
ur
&.
Trong hình học vi phân người ta đã chứng minh
0
dr
t
ds
=
r
r
⇒
0
Vs.t
=
ur
r
&
.
Chiếu lên các trục tọa độ tự nhiên ta được: t
Vs
=
&
; nb
VV0
==
(6.10)
Chú ý
t
VV
=
ur
.
5. Gia tốc điểm.
Trong hệ tọa độ tự nhiên, vectơ gia tốc được xác định theo công thức:
tnb
000
.t.n.b
WWWW=++
uur
r
r
r
.
Theo định nghĩa :
()
0
t0t0t0t0t
dt
dVd
V.tVtVtVtV
dtdtdt
W===+=+
ur
r
uur
rrrr
&
&&
⇔ 0
t0t
dt
ds
VtV
dsdt
W=+×
r
uur
r
&. Hình học vi phân đã chứng minh
00
dtn
ds =
ρ
r
r
vì vậy ta có:
2
00t
t0tt0ttt00
nnV
ds
VtVVtVVvtn
dt
W=+×=+×=+
ρρρ
rr
uur
rrr
r
&&
&
(Chú ý:
t
ds
V
dt
=
)
Đặt t
t0
V.t
W=
uur
r
&
và 2
nt
0
V
.n
W=ρ
uur
r
ta được:
tn
WWW
=+
uuruuruur
(6.11)
- t
t
t0
dV
V.t
dt
W==
ur
uur
r
& gọi là gia tốc tiếp tuyến hướng theo tiếp tuyến với quỹ đạo và
phản ánh sự biến đổi vận tốc về trị số.
M
1
M
1
V
ur
1
V
ur
V
ur
∆ϕ
s
∆