17
CHƯƠNG 9: CHUYỂN ĐỘNG SONG PHẲNG CỦA VẬT RẮN .
I. ĐỊNH NGHĨA, MÔ HÌNH. PHƯƠNG TRÌNH CHUYỂN ĐỘNG.
1. Định nghĩa và ví dụ.
a, Định nghĩa: Chuyển động song phẳng của vật rắn là chuyển động mà trong đó mỗi
điểm thuộc vật luôn di chuyển trong một mặt phẳng cố định và song song với một mặt
phẳng quy chiếu chọn trước.
b, Ví dụ:
- Chiếc xe chuyển động trên sàn phẳng, mỗi điểm thuộc thùng xe chuyển động trên
một mặt phẳng song song với mặt phẳng sàn. Như vậy thùng xe chuyển động song phẳng.
- Bánh xe lăn trên đường cong phẳng song song với mặt phẳng bánh xe, mỗi điểm
trên bánh xe dều chuyển động trong một mặt phẳng song song với mặt phẳng của bánh.
Vậy bánh xe chuyển động song phẳng.
- Cơ cấu tay quay thanh truyền, cơ cấu 4 khâu … là các cơ cấu chuyển động song
phẳng.
- Chuyển động quay quanh trục cố định, chuyển động tịnh tiến phẳng là các trường
hợp riêng của chuyển động song phẳng.
2. Mô hình và thực chất của chuyển động
song phẳng.
a, Mô hình nghiên cứu:
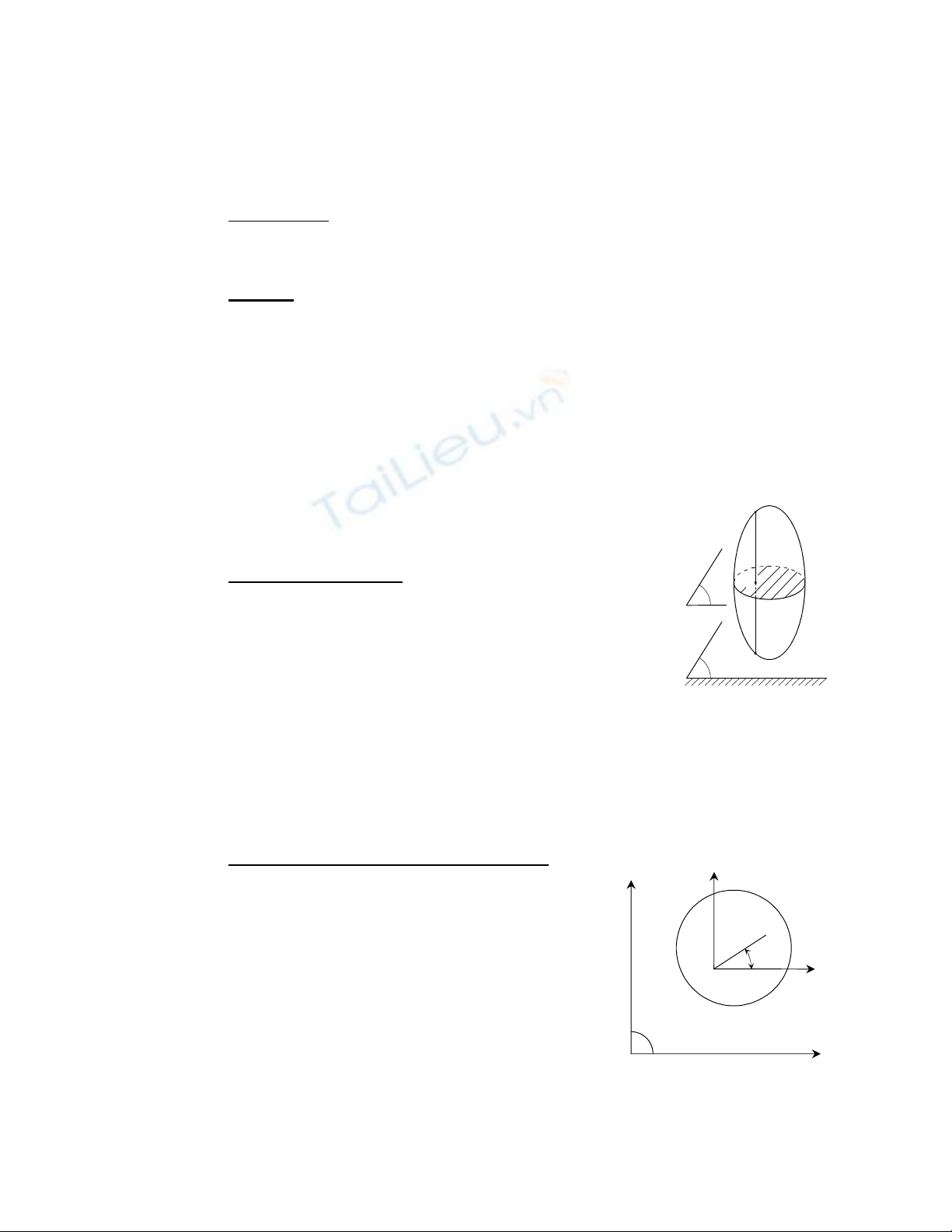
- Giả sử vật rắn ∑ chuyển động song phẳng, theo định nghĩa
thì điểm M chuyển động trên mặt phẳng
π
song song với mặt phẳng
quy chiếu
0
π
như hình vẽ.
- Mặt phẳng
π
giao vật rắn ∑ tạo thành thiết diện (hình phẳng)
S. Qua M dựng đường thẳng vuông góc
π
cắt vật rắn tại A,B.
- Khi vật rắn chuyển động song phẳng thì AB chuyển động tịnh tiến nên mọi điểm
thuộc AB đều chuyển động giống M. Tương tự các đoạn thẳng khác thuộc vật rắn vuông
góc
π
cũng chuyển động tịnh tiến.
- Ta có thể kết luận: Nghiên cứu chuyển động của vật rắn chuyển động song phẳng
có thể quy về nghiên cứu chuyển động của hình phẳng S trong mặt phẳng
π
. Chuyển động
của vật rắn chuyển động song phẳng có thể coi là chuyển động phẳng.
b, Thực chất của chuyển động song phẳng:
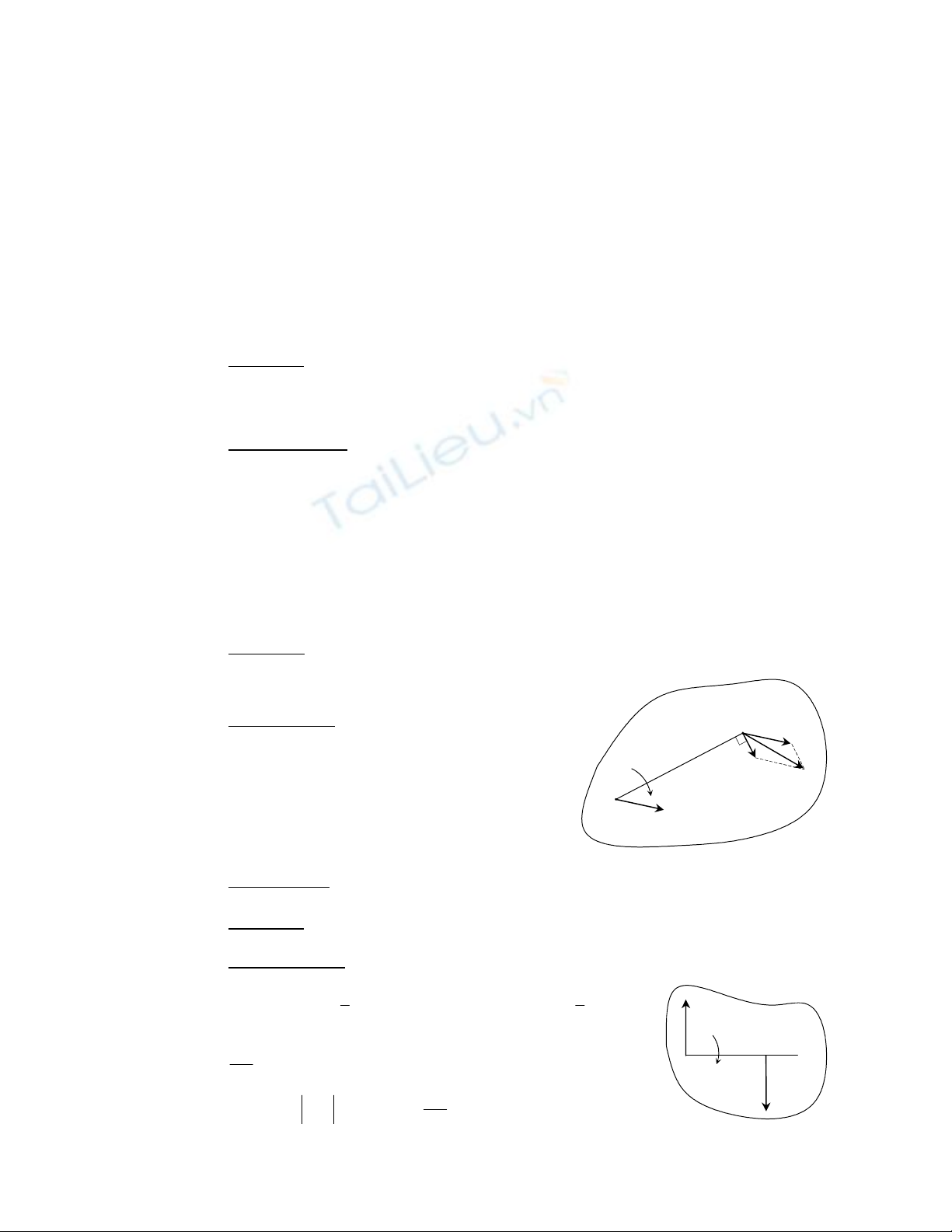
- Trên hình phẳng S ta gắn một hệ quy chiếu động
Oxy với gốc O gắn chặt với S còn Ox, Oy luôn song song
với các trục O1x1 và O1y1 của hệ cố định.
- Chuyển động của hình phẳng S có thể phân thành
các chuyển động cơ bản là:
• Chuyển động tịnh tiến cùng với hệ động
Oxy so với hệ cố định O1x1y1.
• Chuyển động quay quanh O trong hệ động.
- Như vậy thực chất của chuyển động song phẳng
là tổng hợp hai chuyển động là chuyển động tịnh tiến và
chuyển động quay. Bao giờ cũng có thể phân tích chuyển động song phẳng thành hai
chuyển động cơ bản là chuyển động tịnh tiến của hệ động so với hệ cố định và chuyển
động quay quanh cực O trong hệ động.
M S
A
B
0
π
π
1
O
Ο
π
X
1
Y
X
Y
S
I
α
18
3. Phương trình chuyển động song phẳng của vật rắn.
Theo phân tích trên ta có vị trí của hình phẳng S được xác định bằng ba thông số là
tọa độ điểm cực O trong hệ cố định là
oo
x,y
và góc quay của S quanh O là ϕ.
Như vậy phương trình chuyển động của thiết diện S có dạng:
(
)
()
()
OO
OO
xxt
yyt
t
=
=
ϕ=ϕ
(9.1)
II. VẬN TỐC CÁC ĐIỂM THUỘC VẬT RẮN CHUYỂN ĐỘNG SONG PHẲNG.
1. Định lý liên hệ vận tốc.
a, Định lý: Vận tốc điểm B tuỳ ý thuộc hình phẳng S chuyển động phẳng, bằng tổng
hình học của vận tốc điểm cực A và vận tốc của điểm B quay quanh A.
BABA
VVV
=+
ururur
(9.2)
b, Chứng minh:
Điểm B tham gia hai chuyển động nên ta dùng định lý hợp vận tốc:
aer
VVV
=+
ururur
(*)
-
a
V
ur
là vận tốc tuyệt đối của B, vậy
Ba
VV
=
urur
.
-
e
V
ur
là vận tốc theo của hệ động chính là vận tốc của điểm cực, vậy
Ae
VV
=
urur
.
-
r
V
ur
là vận tốc tương đối của B chính là vận tốc quay của B quanh A, vậy
BAr
VV
=
urur
.
Thay vào (*) ta được (9.2), định lý đã được chứng minh.
2. Định lý hình chiếu vận tốc.
a, Định lý: Hình chiếu vận tốc của hai điểm bất kỳ thuộc hình phẳng lên trục đi qua
hai điểm ấy bằng nhau.
AB
ABAB
hcVhcV
=
urur
(9.3)
b, Chứng minh:
Chiếu đẳng thức (9.2) lên AB ta được:
BABA
ABABAB
hcVhcVhcV
=+
ururur
.
Do BA
VAB
⊥
ur
nên BA
AB
hcV0
=
ur
⇒
BA
ABAB
hcVhcV
=
urur
(ĐPCM).
3. Tâm vận tốc tức thời.
a, Định nghĩa: Điểm P trên hình phẳng S mà tại thời điểm khảo sát có vận tốc bằng
không, gọi là tâm vận tốc tức thời.
b, Định lý: Tại mỗi thời điểm nếu ω≠0, tồn tại duy nhất một tâm vận tốc tức thời.
c, Chứng minh:
- Chứng minh sự tồn tại của tâm vận tốc tức thời:
Giả sử ta biết
ω
và
A
V
ur
. Quay
A
V
ur
theo chiều
ω
một góc
90o ta được nửa đường thẳng AB. Trên AB lấy điểm P sao cho:
A
V
AP =
ω
. Theo định lý liên hệ vận tốc ta có:
PAPA
VVV
=+
ururur
Ta thấy A
PA
A
V
V.AP.V
=ω=ω=
ω
ur
, mặc khác
PA
V
ur
cùng
A
B
ω
A
V
ur
A
V
ur
BA
V
ur
B
V
ur
A P B
A
V
ur
PA
V
ur
ω
19
phương, ngược chiều với
A
V
ur
nên ta có:
PAA
VV
=−
urur
. Thay vào ta có
PAPA
VVV
=+
ururur
, hay
PAA
VVV0
=−=
ururur
. Như vậy tồn tại điểm P có vận tốc bằng 0.
- Chứng minh tính duy nhất của tâm vận tốc tức thời:
Giả sử có hai điểm P1 và P2 tại thời điểm khảo sát có vận tốc bằng 0. Viết định lý
liên hệ vận tốc cho P
1 và P
2
ta được:
2112
PPPP
VVV
=+
ururur
. Vì 21
PP
VV0
==
urur
nên
12
PP 12
V.PP0
=ω=
ur
. Điều này vô lý, như vậy tâm vận tốc tức thời là duy nhất.
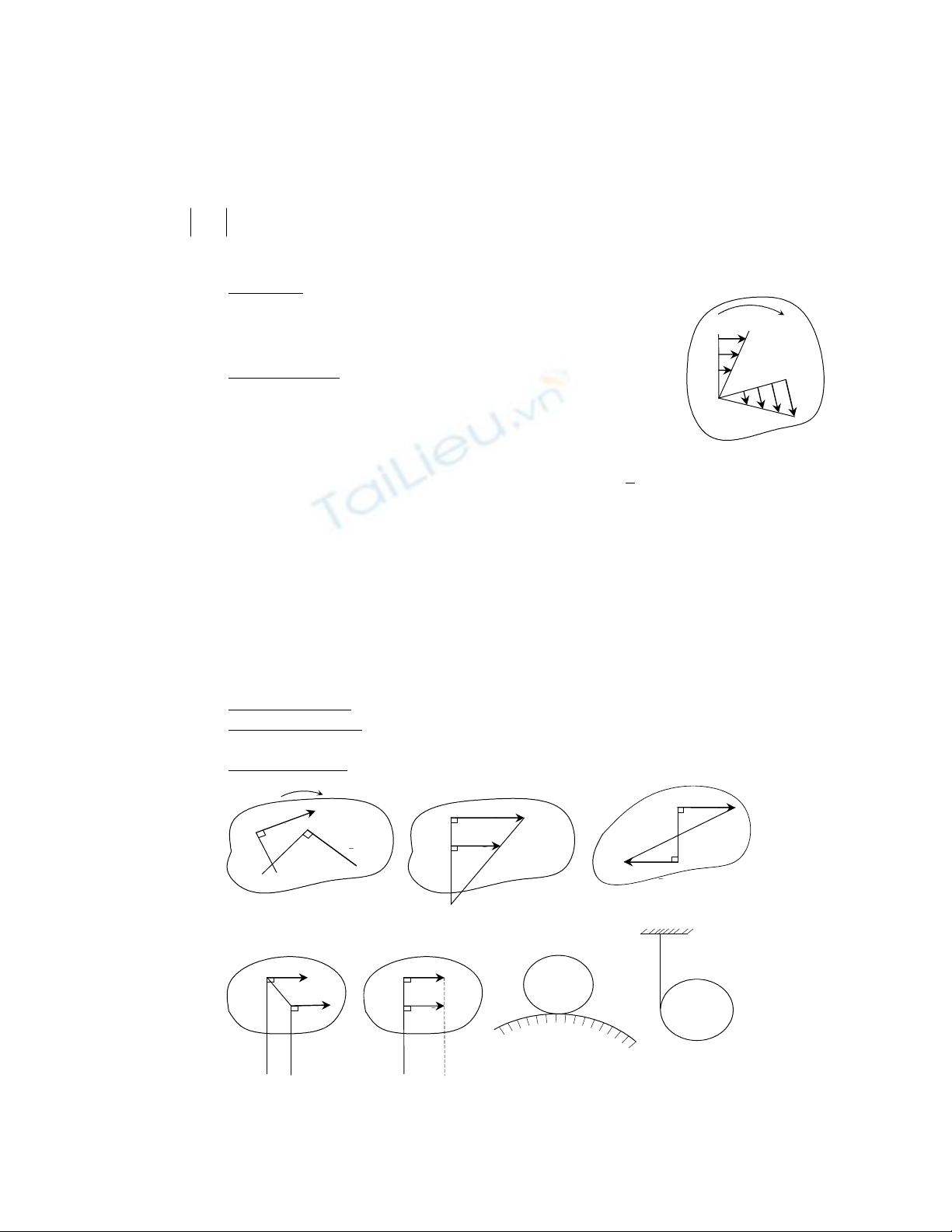
4. Định lý phân bố vận tốc.
a, Định lý: ở mỗi thời điểm vận tốc các điểm thuộc hình phẳng
nói chung được phân bố như hình phẳng ấy đang quay quanh tâm
vận tốc tức thời với vận tốc gócω. Nếu ω =0 thì hình phẳng chuyển
động tịnh tiến tức thời.
b, Chứng minh:
- Xét trường hợp
0
ω≠
: Viết định lý liên hệ vận tốc của điểm
A bất kỳ với điểm cực P ta có:
APAP
VVV
=+
ururur
, Vì P
V0
=
ur
nên
AAP
VV
=
urur
.
A
V
ur
có
.AP
AP
Phöông AP
Chieàu höôùng theo chieàu
Ñoä lôùn V
⊥
ω
=ω
- Xét trường hợp
0
ω=
: Viết định lý liên hệ vận tốc của điểm A bất kỳ với điểm
cực P ta có:
APAP
VVV
=+
ururur
, Vì
0
ω=
nên AP
V0
=
ur
⇒
AP
VV
=
urur
.
Vậy vận tốc các điểm như nhau nên hình phẳng chuyển động tịnh tiến tức thời. Định
lý đã được chứng minh.
5. Quy tắc thực hành tìm tâm vận tốc tức thời.
Dựa vào các kết quả trên ta tìm được một số quy tắc thực hành xác định tâm vận tốc
tức thời như sau:
a, Trường hợp 1: Biết vận tốc điểm A và phương vận tốc điểm B. Hình (a).
b, Trường hợp 2: Biết vận tốc điểm A, B và phương của chúng song song.
Hình(b,c,d)
c, Trường hợp 3: Biết một điểm thuộc hình phẳng có vận tốc bằng không.Hình(e)
ω
A
B
P
A
V
ur
B
V
ur
Hình a
P
A
B
A
V
ur
B
V
ur
Hình b
A
B
P
A
V
ur
B
V
ur
Hình c
P
(S)
(S)
P
Hình e
A
B
A
V
ur
B
V
ur
P
→
∞
A
B
A
V
ur
B
V
ur
P
→
∞
Hình d
P
A
B
A
V
ur
B
V
ur
ω