7
CHƯƠNG 12: HÌNH HỌC KHỐI LƯỢNG
I. KHỐI TÂM CỦA CƠ HỆ.
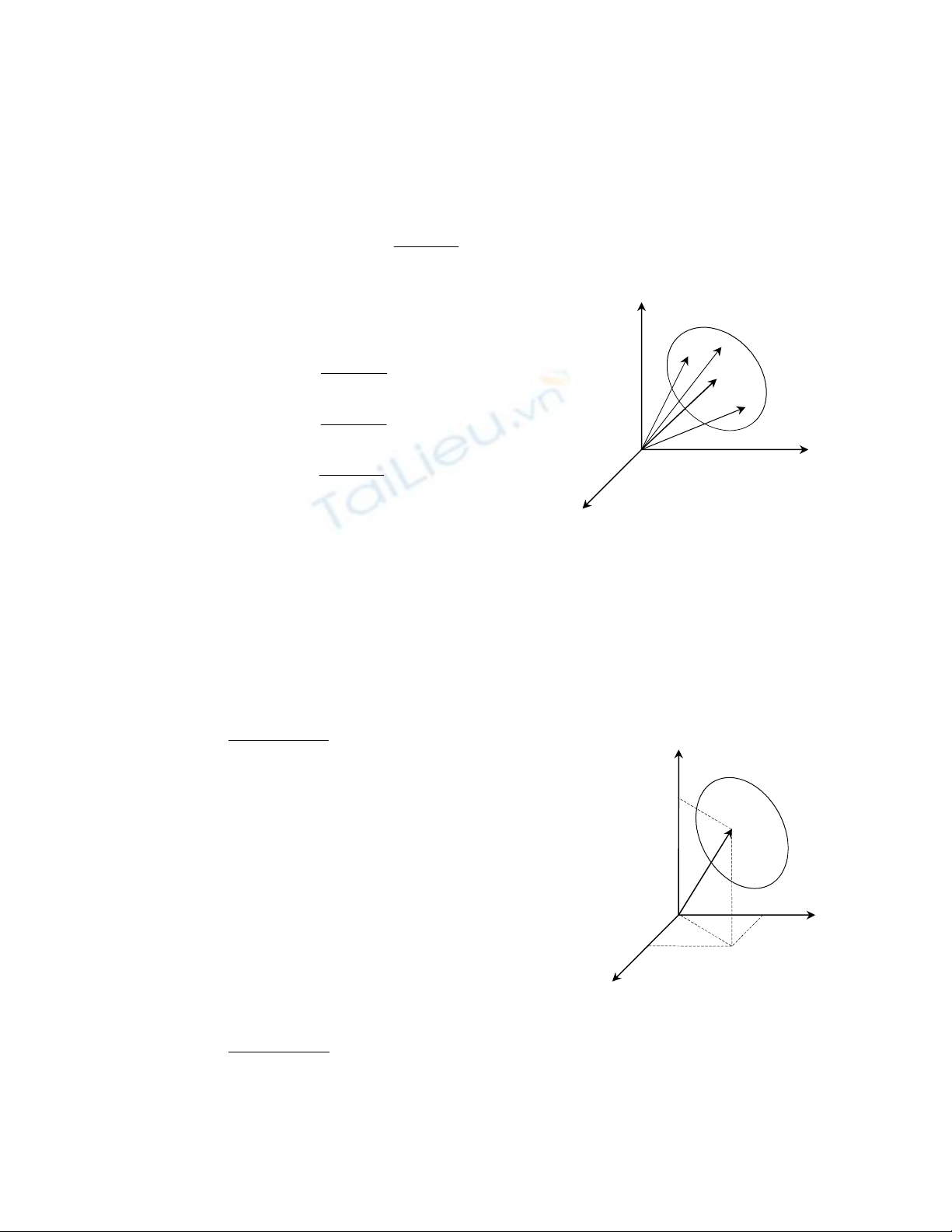
Xét hệ chất điểm
1
M
,
2
M
,...,
n
M
có khối lượng tương ứng là
1
m
,
2
m
,...,
n
, có các
vectơ định vị tương ứng là
1
r
r
,
2
r
r
,...,
n
r
r
. Khối tâm của cơ hệ là một điểm hình học C được
xác định theo công thức:
KK
C
m.r
r
M
=
∑
r
r (12.1)
Trong đó
C
r
r
là vectơ định vị khối tâm cơ hệ,
K
Mm
=
∑
là khối lượng của cả hệ.
Chiếu (12.1) lên các trục tọa độ ta được:
KK
C
KK
C
KK
C
mx
xM
my
yM
mz
zM
=
=
=
∑
∑
∑
(12.2)
Với
C
x
,
C
y
,
C
z
là tọa độ điểm C,
K
x
,
K
y
,
K
z
là
tọa độ chất điểm thứ K.
Nếu cơ hệ ở gần mặt đất thì khối tâm của cơ hệ trùng với trọng tâm của nó. Nhân cả
tử và mẫu của (12.1) hoặc (12.2) với gia tốc trọng trường g ta sẽ nhận được các công thức
trọng tâm của hệ. Khối tâm của cơ hệ luôn tồn tại còn trọng tâm thì chỉ tồn tại khi cơ hệ ở
gần mặt đất.
II. MÔMEN QUÁN TÍNH CỦA VẬT RẮN.
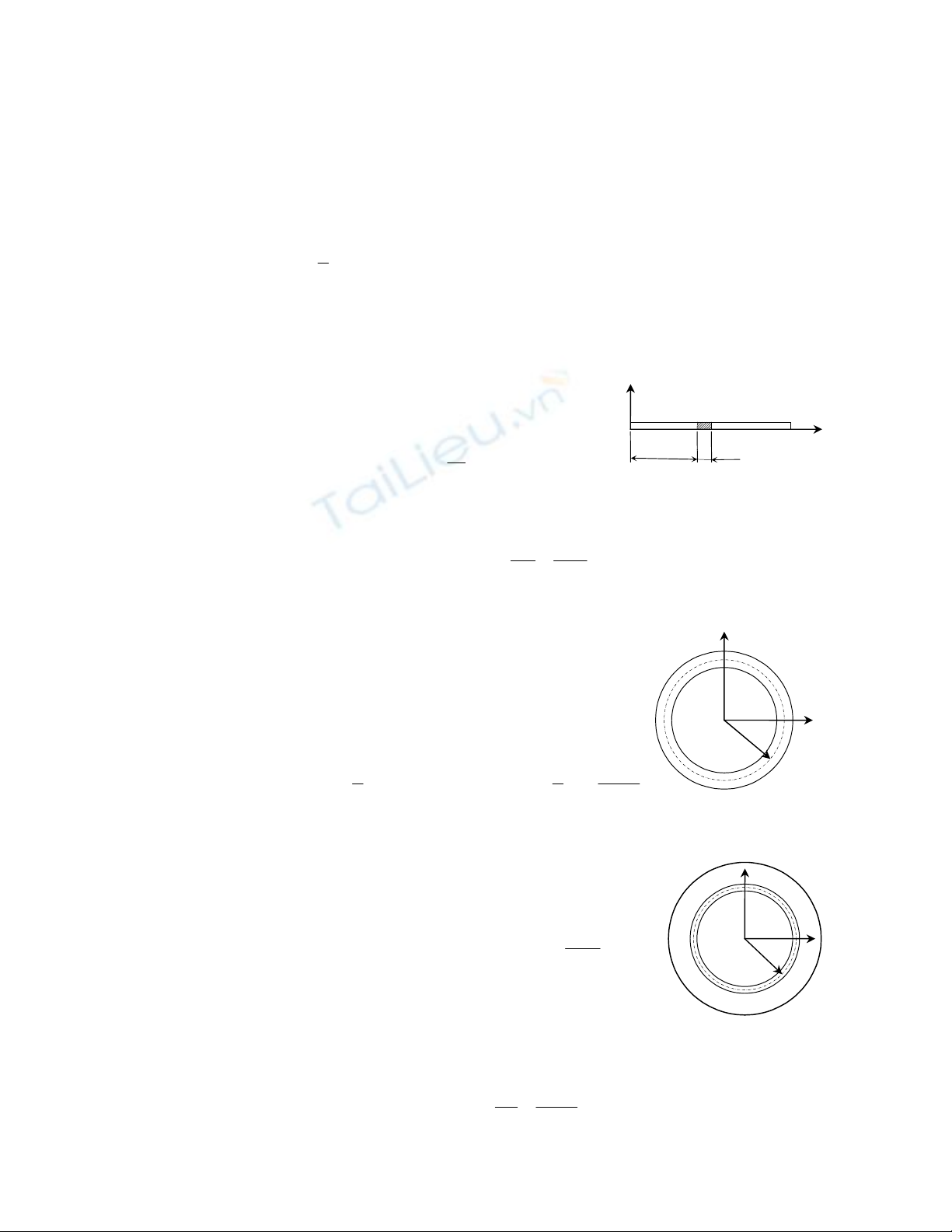
1. Mômen quán tính của vật đối với trục.
a, Định nghĩa: Mômen quán tính của vật rắn đối với trục z (ký hiệu là
z
J
) là đại lượng vô
hướng, được xác định theo công thức:
2
zKK
Jm.d
=
∑
. (12.3)
Trong công thức trên
K
m
là khối lượng chất điểm
K
M
,
K
d
là khoảng cách từ chất điểm
K
M
đến trục z.
Gọi
K
x
,
K
y
,
K
z
là tọa độ chất điểm
K
M
. Ta dễ
dàng chứng minh được:
22
xKKK
22
yKKK
22
zKKK
Jm.(yz)
Jm.(xz)
Jm.(xy)
=+
=+
=+
∑
∑
∑
(12.4)
2. Mômen quán tính của vật đối với
điểm.
a, Định nghĩa: Mômen quán tính của vật rắn đối với điểm O, ký hiệu là
O
J
đại lượng vô
hướng, được xác định theo công thức:
2
OKK
Jm.r
=
∑
. (12.5)
O
X
Y
Z
1
M
2
M
n
M
C
1
r
r
2
r
r
C
r
r
n
r
r
Y
O
X
Z
K
M
K
r
r
y
x
z
k
d
8
Trong công thức trên
K
m
là khối lượng chất điểm
K
M
,
K
r
là khoảng cách từ chất
điểm
K
M
đến điểm O.
3. Mối liên hệ giữa mômen quán tính của vật đối với điểm và
trục.
Ta có
2222222
xyzKKKKKKKKKKO
JJJm.(2x2y2z)2m.(xyz)2m.r2J
++=++=++==
∑∑∑
.
Hay là:
()
Oxyz
1
JJJJ
2
=++ (12.6)
III. MÔMEN QUÁN TÍNH CỦA MỘT SỐ VẬT ĐỒNG CHẤT.
1. Đối với thanh mỏng đồng chất.
Xét thanh mỏng AB có khối lượng M và chiều dài L.
Chia thanh làm nhiều phần tử dọc theo chiều dài thanh. Xét
một phần từ cách trục Ay là
K
x
, có độ dài là
K
x
∆
. Khối
lượng của nó là
KK
m.x
=γ∆
, với
M
l
γ=
là khối lượng một
đơn vị chiều dài thanh.
Mômen quán tính của thanh với trục Ay là:
22
AyKKKK
Jm.xx.x
==γ∆
∑∑
. Chuyển tổng
này qua giới hạn ta nhận được: l
32
2
Ay
0
.lM.l
J.xdx
33
γ
=γ==
∫ (12.7)
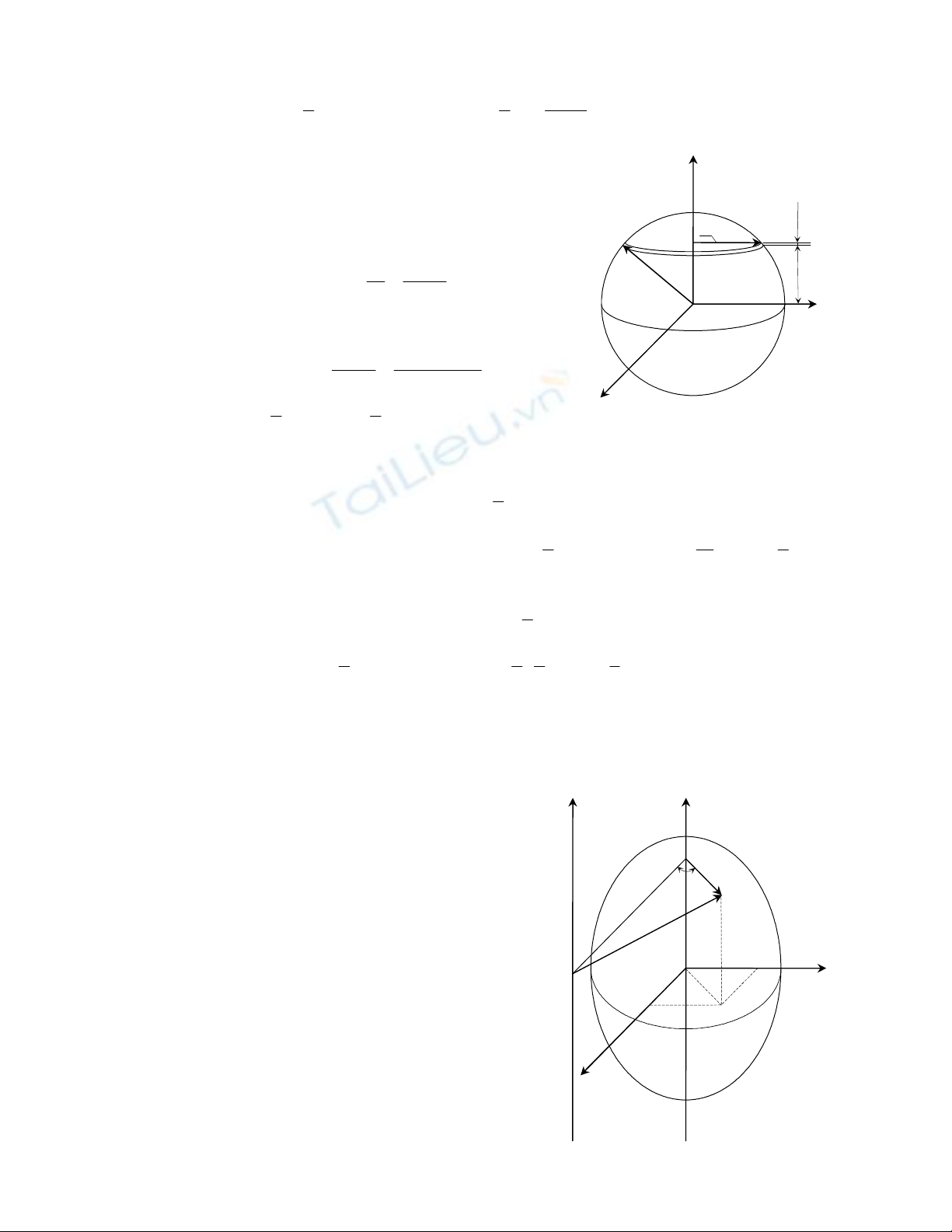
2. Đối với vòng tròn, vỏ trụ tròn đồng chất.
Xét vòng tròn hoặc vỏ trụ tròn đồng chất có khối lượng M
và bán kính R. Chia vòng tròn hoặc vỏ trụ tròn làm nhiều phần tử
nhỏ. Xét phần tử thứ K có khối lượng của nó là
K
m
.
Mômen quán tính của vòng tròn hoặc vỏ trụ tròn với trục
z qua tâm và vuông góc với mặt phẳng của nó là:
22
zK
Jm.RM.R
==
∑
(12.8)
Chú ý
()
Ozxyz
1
JJJJJ
2
==++ ⇒
2
xyz
1M.R
JJJ
22
===
(12.9)
3. Đối với tấm tròn, khối trụ tròn đồng chất.
Xét tấm tròn hoặc khối trụ tròn đồng chất có khối lượng M và
bán kính R. Chia tấm tròn hoặc khối trụ tròn làm nhiều vành tròn
nhỏ. Xét vành tròn thứ K có bán kính
K
r
, bề dày vành tròn là
K
r
∆
.
Khối lượng của vành tròn là
kkk
m.2.r.r
=γπ∆
, với
2
M
.R
γ=π là khối
lượng một đơn vị diện tích tấm.
Mômen quán tính của tấm tròn hoặc khối trụ tròn với trục z
qua tâm và vuông góc với mặt phẳng của nó là:
23
zkkKKk
J.2.r.r.r2.r.r
=γπ∆=πγ∆
∑∑
(12.10)
Chuyển tổng này qua giới hạn ta nhận được:
R
42
3
z
0
RM.R
J2.r.dr2.
42
=πγ=πγ=
∫ (12.11)
k
X
k
X
∆
A B
x
y
Y
X
R
ur
Y
X
k
r
r
9
Chú ý
()
Ozxyz
1
JJJJJ
2
==++ ⇒
2
xyz
1M.R
JJJ
24
=== (12.12)
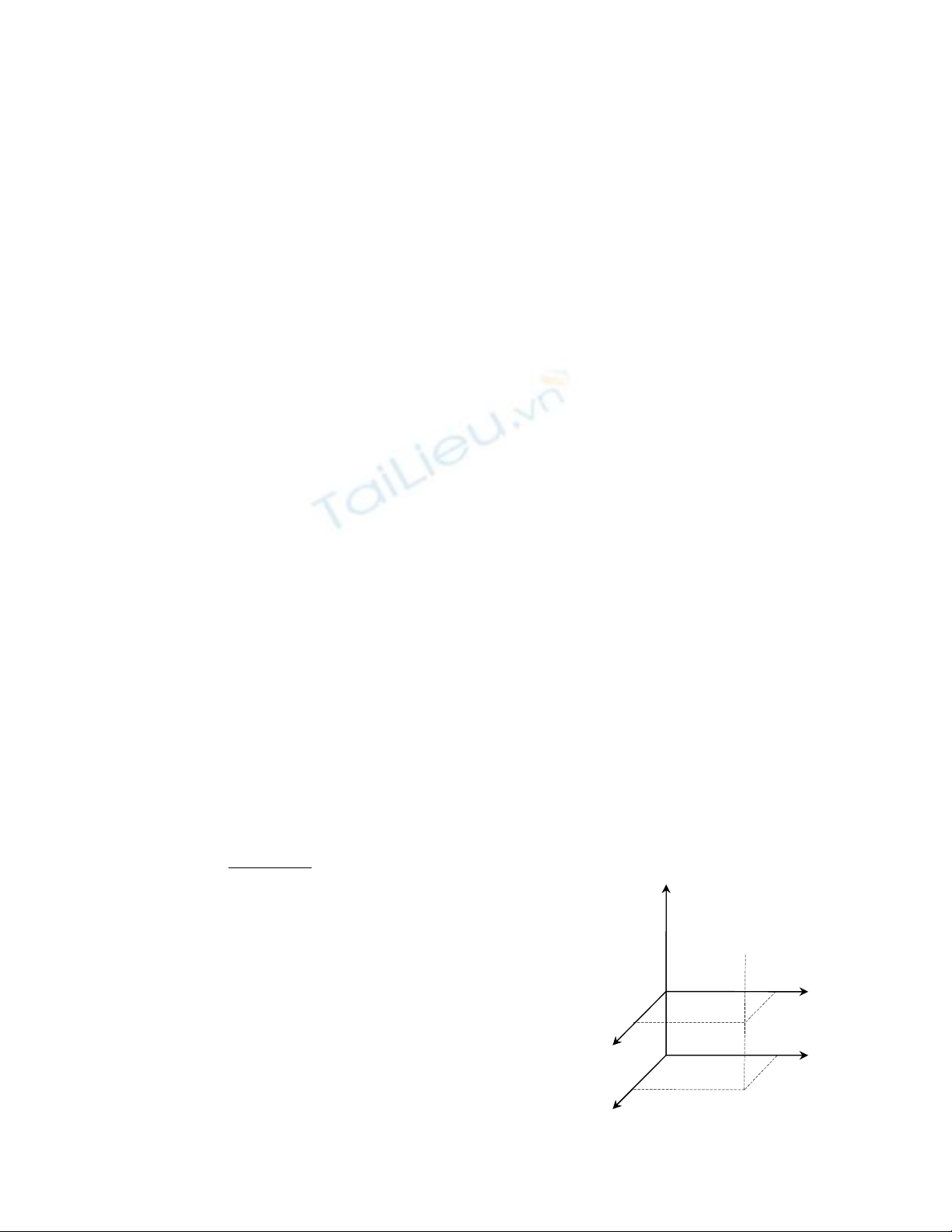
4. Đối với khối cầu đồng chất.
Xét khối cầu đồng chất có khối lượng M và bán
kính R. Chia khối cầu làm nhiều tấm tròn mỏng song song
với mặt phẳng Oxy. Xét tấm tròn thứ K có bán kính
K
r
, bề
dày tấm tròn
K
z
∆
. Khối lượng của tấm tròn là
2
kKk
m..r.z
=γπ∆
, với
3
M3.M
V4.R
γ==
π là khối lượng một
đơn vị thể tích.
Mômen quán tính của tấm tròn với trục z là:
222
KKKkK
z
m.r..r.z.r
J
22
γπ∆
∆==
()
2
422
KkKk
11
..r.z..Rz.z
22
=γπ∆=γπ−∆
Mômen quán tính khối cầu với trục z là tổng mômen quán tính của các tấm tròn với
trục đó, vậy ta có:
()
2
22
zzKk
1
JJ..Rz.z
2
=∆=γπ−∆
∑∑
Chuyển tổng qua giới hạn ta được:
()
R2
2252
zK
R
182
J..Rz.dz..RMR
2155
−
=γπ−=γπ=
∫
(12.13)
Vì tính đối xứng nên ta có :
2
xyz
2
JJJMR
5
=== .
Mặc khác
()
Oxyz
1
JJJJ
2
=++ nên
22
O
323
JMRMR
255

==

 (12.14)
IV. MÔMEN QUÁN TÍNH CỦA VẬT ĐỐI VỚI CÁC TRỤC SONG SONG.
1. Định lý: Mômen quán tính của vật với trục
1
z
nào đó bằng tổng mômen quán tính
của nó đối với trục z song song
1
z
đi qua khối
tâm của vật và tích khối lượng của vật với bình
phương khoảng cách giữa hai trục ấy:
2
z1Cz
JJM.d
=+ (12.15)
Chứng minh: Dựng hệ quy chiếu Cxyz có
Cz song song
1
z
, trục
1
z
nằm trong mặt phẳng
Cxz. Theo định nghĩa ta có:
2
z1K1K
Jm.r
=
∑
;
2
zCKK
Jm.r
=
∑
.
Xét tam giác ABMK ta có:
222
1KKK
rrd2.d.r.c
os
=+−α
mà
KK
r.cx
os
α=
⇒
222
1KKK
rrd2.d.x
=+− thay vào ta có:
(
)
222
z1K1KKKK
Jm.rm.rd2.d.x
==+−
∑∑
⇒
22
z1KKKKK
Jm.rm.d2.dm.x
=+−
∑∑∑
(*)
O Y
X
Z
k
r
r
R
ur
Z
k
∆Z
k
C
Y
X
Z
1
Z
A
B
k
M
k
r
r
1k
r
r
α
d
k
x
k
y
10
Theo công thức (12.2) ta có:
KKC
m.xM.x0
==
∑
(vì
C
x
=0).
Vậy (*) trở thành:
222
z1KKKzC
Jm.rm.dJM.d
=+=+
∑∑
(ĐPCM)
Nhận xét: Trong các trục có cùng phương thì mômen quán tính đối với trục qua khối
tâm có giá trị bé nhất.
V. MÔMEN QUÁN TÍNH CỦA VẬT ĐỐI VỚI CÁC TRỤC CẮT NHAU TẠI MỘT
ĐIỂM.
Định lý: Mômen quán tính của vật đối với trục
∆
đi qua gốc tọa độ với các góc chỉ
phương là
,,
αβγ
có biểu thức xác định là:
xyzxyyzzx
JJcJcJc2.Jc.c2.Jc.c2.Jc.c
222
ososososososososos
∆
=α+β+γ−αβ−βγ−γα
(12.16)
Trong đó
22
xKKK
22
yKKK
22
zKKK
Jm.(yz)
Jm.(xz)
Jm.(xy)
=+
=+
=+
∑
∑
∑; và
yzKKK
zxKKK
xyKKK
Jm.y.z
Jm.z.x
Jm.x.y
=
=
=
∑
∑
∑ ta được:
Các đại lượng
yzzxxy
J,J,J
được gọi là những mômen tích quán tính (còn có tên là
mômen quán tính ly tâm). Từ (12.6) ta có thể tính mômen quán tính của trục bất kỳ khi biết
sáu đại lượng trên.
VI. CÁC ĐỊNH LÝ VỀ TRỤC QUÁN TÍNH CHÍNH VÀ TRỤC QUÁN TÍNH CHÍNH
TRUNG TÂM.
1. Định nghĩa về trục quán tính chính và trục quán tính chính trung tâm.
TrụcOz được gọi là trục quán tính chính tại O nếu thỏa mãn điều kiện:
zxzy
JJ0
==
(12.17)
TrụcOz được gọi là trục quán tính chính trung tâm nếu nó là trục quán tính chính và
đi qua khối tâm của vật rắn.
Mômen quán tính của vật đối với trục quán tính chính được gọi là mômen quán tính
chính, và đối với trục quán tính chính trung tâm được gọi là mômen quán tính chính trung
tâm. Chú ý: Người ta đã chứng minh được rằng : Tại mỗi điểm của vật có ba trục quán
tính chính vuông góc với nhau.
2. Các định lý.
a, Định lý 1: Trục quán tính chính của vật rắn tại điểm O, không đi qua khối tâm của
vật thì nó chỉ là trục quán tính chính của vật tại điểm O.
Chứng minh: Giả sử Oz là trục quán tính chính
của vật tại O. Ta sẽ chứng minh nó không phải là trục
quán tính chính của vật tại điểm O1 nào đó. Ta lấy O1
trên Oz và cách O là d. Gắn vào O, O1 các hệ trục tọa
độ như hình vẽ. Vì Oz là trục quán tính chính của vật
rắn tại O nên zxzy
JJ0
==
.
Ta có:
(
)
zxKKKKKK
Jm.z.xm.zd.x
′′ ′′
==−
∑∑
(
)
zxKKKKKKKK
zxzxCC
Jm.zd.xm.z.xdm.x
JJM.x.dM.x.d
′′
′′
=−=−
=−=−
∑∑∑
Z
X
Y
Y’
X’
O
O’
k
M
k
x
k
y
k
y
′
k
x
′
11
Vì Oz không đi qua khối tâm C nên C
x0
≠
, vậy zx
J0
′′
≠
. Rõ ràng trục Oz không
phải là trục quán tính chính của vật rắn tại O1.
b, Định lý 2: Trục quán tính chính trung tâm của vật là trục quán tính chính của mọi
điểm trên trục ấy.
Chứng minh: Ta thấy khi Oz là trục trục quán tính chính trung tâm thì nó đi qua
khối tâm C, tức là C
x0
=
. Vậy zx
J0
′′
=
, tương tự ta cũng chứng minh đượczy
J0
′′
=
. Rõ
ràng trục Oz là trục quán tính chính của mọi điểm thuộc Oz.
c, Định lý 3: Nếu vật rắn đồng chất có một trục đối xứng thì trục đó là trục quán tính
chính trung tâm.
Chứng minh: Gọi trục đối xứng của vật rắn là z thì khối tâm của vạt phải nằm trên
trục này. Nếu vật có phần tử
K
M
có khối lượng
K
m
, có tọa độ
(
)
KKK
x,y,z
thì tương ứng
sẽ có phần tử
K
M
′
đối xứng với
K
M
qua trục z.
K
M
′
có khối lượng
K
m
, có tọa độ
(
)
KKK
x,y,z
−− .Ta có :
(
)
()
yzKKKKKKKKKKKK
zxKKKKKKKKKKKK
Jm.y.zm.y.zm.y.zm.y.z0
Jm.z.xm.z.xm.z.xm.z.x0
=+−=−=
=+−=−=
∑∑∑∑
∑∑∑∑ .
Do đó z là trục quán tính chính, mặc khác z đi qua khối tâm C nên z là trục quán tính
chính trung tâm của vật rắn.
d, Định lý 4: Nếu vật rắn đồng chất có mặt phẳng đối xứng thì trục vuông góc với
mặt phẳng đó là trục quán tính chính tại giao điểm giữa mặt phẳng đối xứng và trục.
Chứng minh: Chọn trục Ox, Oy thuộc mặt phẳng đối xứng. Nếu vật có phần tử
K
M
có khối lượng
K
m
, có tọa độ
(
)
KKK
x,y,z
thì tương ứng sẽ có phần tử
K
M
′
đối xứng với
K
M
qua mặt phẳng Oxy.
K
M
′
có khối lượng
K
m
, có tọa độ
(
)
KKK
x,y,z
−.Ta có :
(
)
()
yzKKKKKKKKKKKK
zxKKKKKKKKKKKK
Jm.y.zm.y.zm.y.zm.y.z0
Jm.z.xm.z.xm.z.xm.z.x0
=+−=−=
=+−=−=
∑∑∑∑
∑∑∑∑ .
Do đó Oz là trục quán tính chính của vật rắn.
Chú ý rằng khối tâm C của vật rắn nằm trên mặt phẳng đối xứng, do vậy trục vuông
góc với mặt phẳng đối xứng tại khối tâm C sẽ là trục quán tính chính trung tâm.