9
CHƯƠNG 2: HỆ LỰC ĐỒNG QUY – HỆ NGẪU LỰC
§I. HỆ LỰC ĐỒNG QUY.
1. Khái niệm về hệ lực đồng quy.
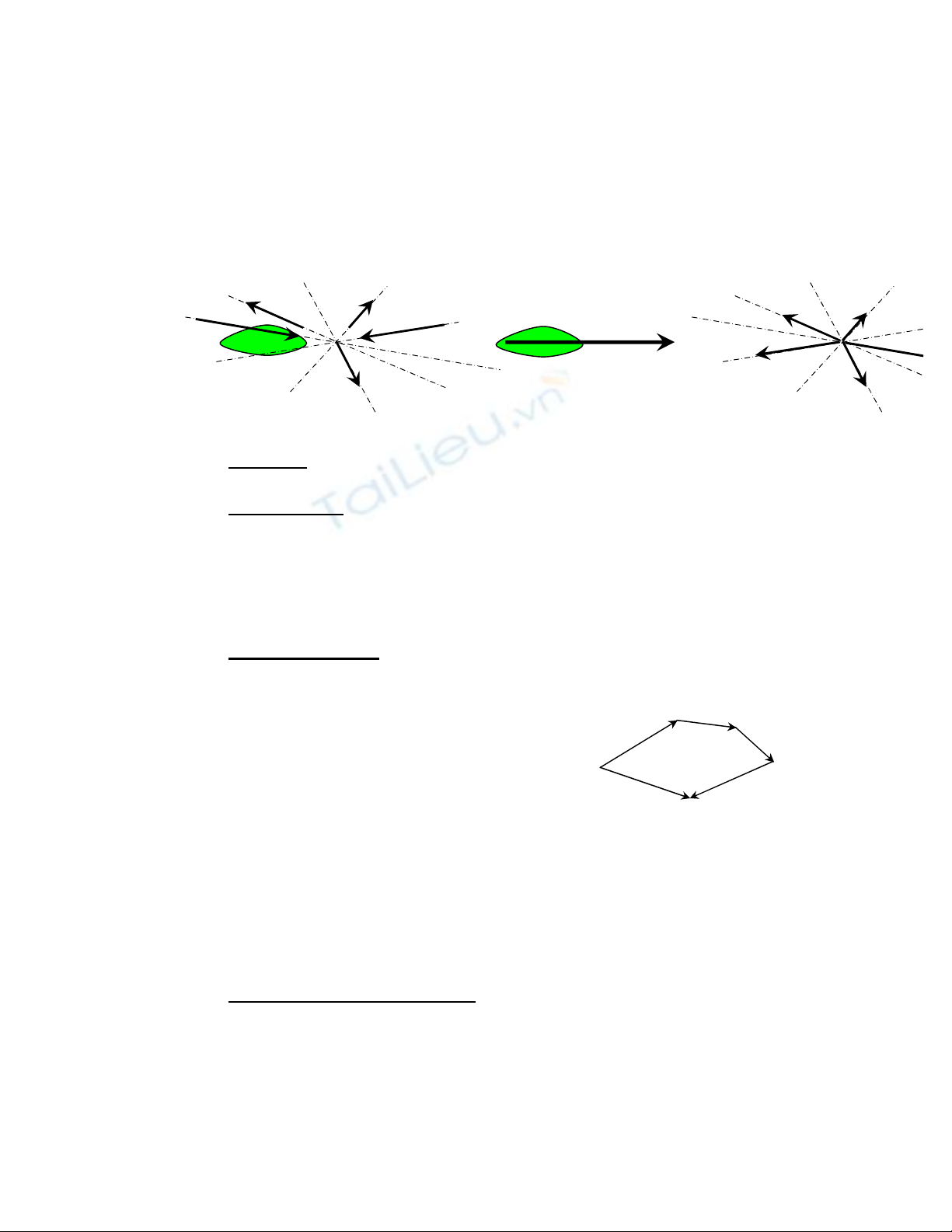
Ø Hệ lực đồng quy là một hệ lực mà các đường tác dụng của chúng đồng quy tại
một điểm.
Ø Theo hệ quả trượt lực, bao giờ ta cũng có thể trượt các lực đã cho theo đường tác
dụng của chúng tới điểm đồng quy của các đường tác dụng.
2. Hợp lực của hệ lực đồng quy.
a. Định lý: Hệ lực đồng quy tương đương với một hợp lực đặt tại điểm đồng quy của
chúng. Vectơ biểu diễn hợp lực bằng tổng hình học của các vectơ biểu diễn các lực đã cho.
b.Chứng minh: Giả sử ta có hệ lực đồng quy
(
)
12n
F,F,...,F
rrr
đặt lên vật rắn tại điểm O.
Theo tiên đề 3 ta có:
121
F+ FR
≡
ururur
đặt tại O, hợp
R
ur
và
3
F
ur
ta được
213123
RR+ FFFF
≡=++
urururururur
đặt tại O. Tiếp tục như vậy ta được:
()
12n
...
n-2n
RR+ F =FFF
≡+++
urururururur
3. Phương pháp xác định hợp lực của hệ lực đồng quy.
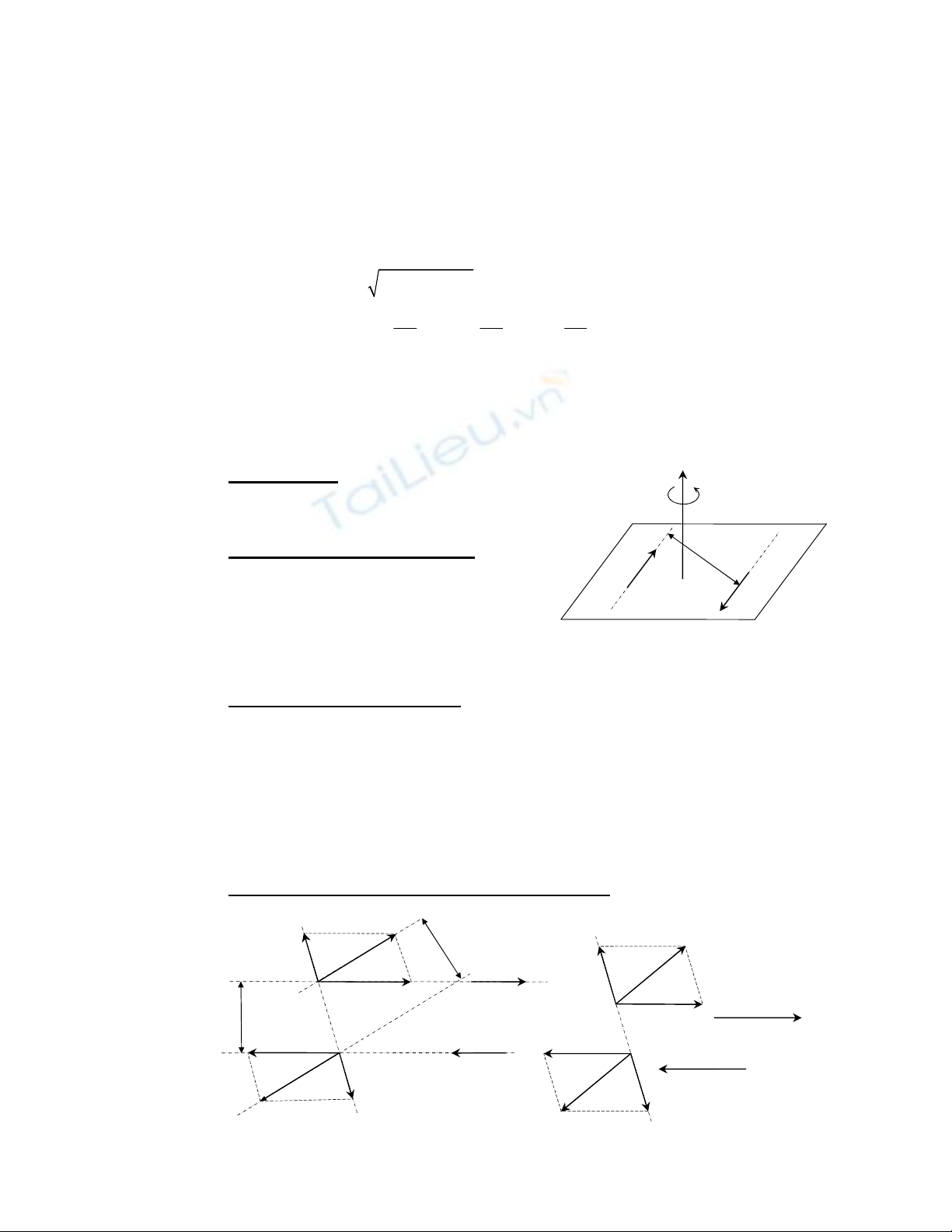
a. Phương pháp vẽ: Lấy một điểm A chọn tuỳ ý làm cực, vẽ các vectơ
A
1
A
uuuur
=
1
F
ur
,
1
AA
2
uuuuur
=
2
F
ur
,…,
n1n
AA
−
uuuuuuur
=
n
F
ur
như hình vẽ. Ta có:
n
AA
uuuur
=
A
1
A
uuuur
+1
AA
2
uuuuur
+…+
n1n
AA
−
uuuuuuur
=
12n
...
FFF
+++
ururur
=
R
′
uur
Vậy
R
′
uur
=
12n
...
FFF
+++
ururur
(2.1)
n
A,A
uuuuuur
=n
k
k1
F
=
∑
ur
được gọi là vectơ chính của hệ
lực đã cho, ký hiệu là
R
′
uur
. Như vậy vectơ biểu diễn
hợp lực của hệ lực đồng quy bằng vectơ chính của hệ lực ấy.
Sự khác nhau giữa vectơ chính
R
′
uur
và hợp lực
R
ur
.
- Vectơ
R
ur
biểu diễn hợp lực của hệ lực đồng quy nên là vectơ trượt và đi qua điểm
đồng quy của hệ lực đã cho.
- Vectơ
R
′
uur
là tổng hình học của các vectơ biểu diễn các lực đã cho nên là vectơ và
vẽ ở đâu cũng được.
b. Phương pháp chiếu (giải tích): Gọi các hình chiếu của lực bất kỳ
k
F
uur
thuộc hệ lực
đã cho là
kx
F
,
ky
F
,
kz
F
hoặc là Xk,Yk,Zk. Hình chiếu vectơ
R
ur
lên các trục toạ độ sẽ lần lượt
bằng tổng đại số của các hình chiếu ấy.
F
r
2
F
r
3
F
r
i
F
r
n
F
r
i
F
r
2
F
r
3
F
r
n
F
r
Trượt lực
A
A1 A2
An
R
′
uur
A3
10
nn
xx1x2xnxkxk
K1K1
nn
yy1y2ynykyk
K1K1
nn
zz1z2znzkzk
K1K1
RRFFFFX
RRFFFFY
RRFFFFZ
==
==
==
′
==+++==
′
==+++==
′
==+++==
∑∑
∑∑
∑∑
L
L
L
(2.2)
Cường độ và hướng của
R
ur
được xác định như sau:
222
xyz
y
xz
RRRR
R
RR
Cos,Cos,Cos
RRR
=++
α=β=γ=
(2.3)
(α, β,γ là góc hợp bởi
R
ur
với Ox, Oy, Oz.)
II.HỆ NGẪU LỰC.
1. Khái niệm về ngẫu lực.
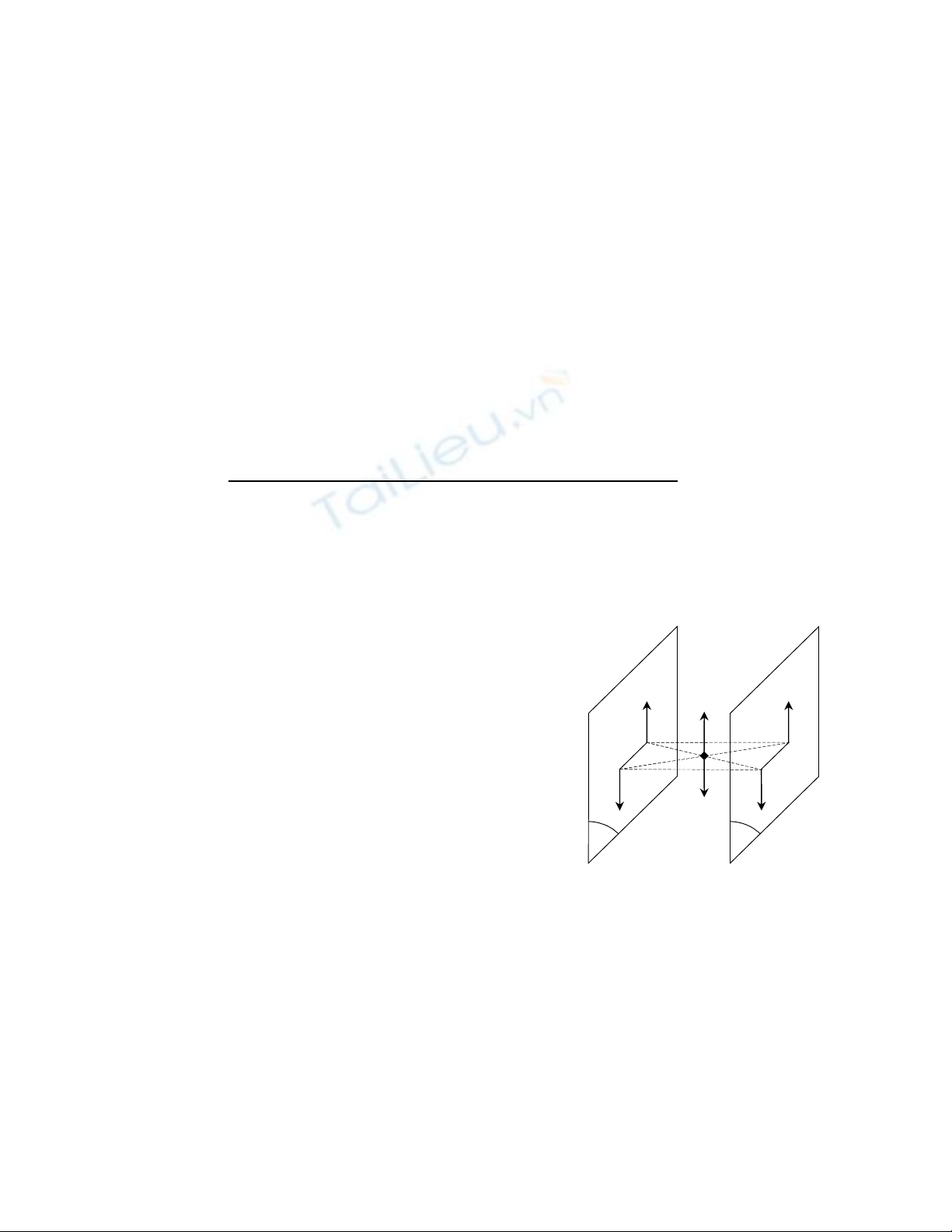
a. Định nghĩa: Ngẫu lực là một hệ lực gồm
hai lực song song ngược chiều và cùng cường độ,
ký hiệu
(
)
′
uruur
F,F
, gọi tắt là ngẫu.
b. Các đặc trưng của ngẫu lực: Ngẫu lực
có 3 đặc trưng cơ bản như sau:
- Mặt phẳng tác dụng: là mặt phẳng chứa
hai lực thành phần .
- Chiều quay của ngẫu lực trong mặt phẳng.
- Cường độ tác dụng của ngẫu lực: bằng tích số
Fd
×
. Trong đó F là giá trị lực
thành phần, d là khoảng cách hai đường tác dụng.
c. Vectơ mômen của ngẫu lực: Để biểu diễn các đặc trưng của ngẫu lực, người ta
dùng vectơ mômen ngẫu lực, ký hiệu
m
uur
có:
- Gốc nằm tuỳ ý trong mặt phẳng tác dụng của ngẫu lực.
- Phương vuông góc với mặt phẳng tác dụng.
- Chiều sao cho khi nhìn từ đầu mút của vectơ xuống mặt phẳng tác dụng thì thấy
chiều quay của ngẫu lực ngược chiều quay kim đồng hồ.
- Độ lớn bằng tích
Fd
×
.
2. Các định lý về biến đổi tương đương ngẫu lực.
a. Định lý 1-Định lý về hai ngẫu lực tương đương: Hai ngẫu lực cùng nằm trong
mặt phẳng có cùng chiều quay và cùng giá trị mômen thì tương đương nhau.
h
2
F
′
ur
1
F
′
ur
F
′
ur
B
A
2
F
r
F
r
F
r
d
Φ
ur
′
Φ
uur
F
r
F
′
ur
P
ur
P
′
uur
Φ
ur
′
Φ
uur
R
ur
R
ur
Trường hợp a Trường hợp b
m
uur
F
r
F
′
ur
d
11
Chứng minh: Giả sử hai ngẫu lực
(
)
F,F
′
uruur
và
(
)
,
′
ΦΦ
uruur
cùng nằm trong một mặt
phẳng, có cùng chiều quay và có cùng giá trị mômen
Φ
F.d = .h
như hình vẽ.
- Trường hợp a: xét trường hợp
F
ur
không //
Φ
ur
. Đường tác dụng của
F
ur
và
Φ
ur
cắt
nhau tại A, của
F
′
uur
và
′
Φ
uur
cắt nhau tại B.
Trượt
F
ur
và
F
′
uur
về các giao điểm A, B như hình vẽ. Theo tiên đề 3, biến đổi
F
ur
,
F
′
uur
thành hai thành phần
1
F
ur
,
2
F
ur
và
1
F
′
uur
,
2
F
′
uur
theo hai phương.
Ta có:
(
)
(
)
1212
FF,F,FF,F
′′′
≡≡
urururuuruuruur
⇒
(
)
(
)
(
)
(
)
12121122
F,FF,F,F,FF,F vaø F,F
′′′′′
≡≡
uruurururuuruururuururuur
.
Rõ ràng
(
)
11
F,F0
′
≡
uruur
⇒
(
)
(
)
22
F,FF,F
′′
≡
uruururuur
2
F.dF.h
⇒=
Theo giả thiết
=Φ
F.d.h
⇒
2
F
=
Φ
, ta dễ thấy
2
F
ur
và
Φ
ur
,
2
F
′
uur
và
′
Φ
uur
cùng đường tác
dụng và cùng chiều ⇒
(
)
(
)
(
)
22
F,F,F,F
′′′
≡ΦΦ≡
uruururuururuur
- Trường hợp b:
ur
F
//
Φ
ur
: Biến đổi (
(
)
(
)
F,FP,P
′′
≡
uruururuur
với
P
ur
không //
F
ur
rồi trở về
trường hợp đầu.
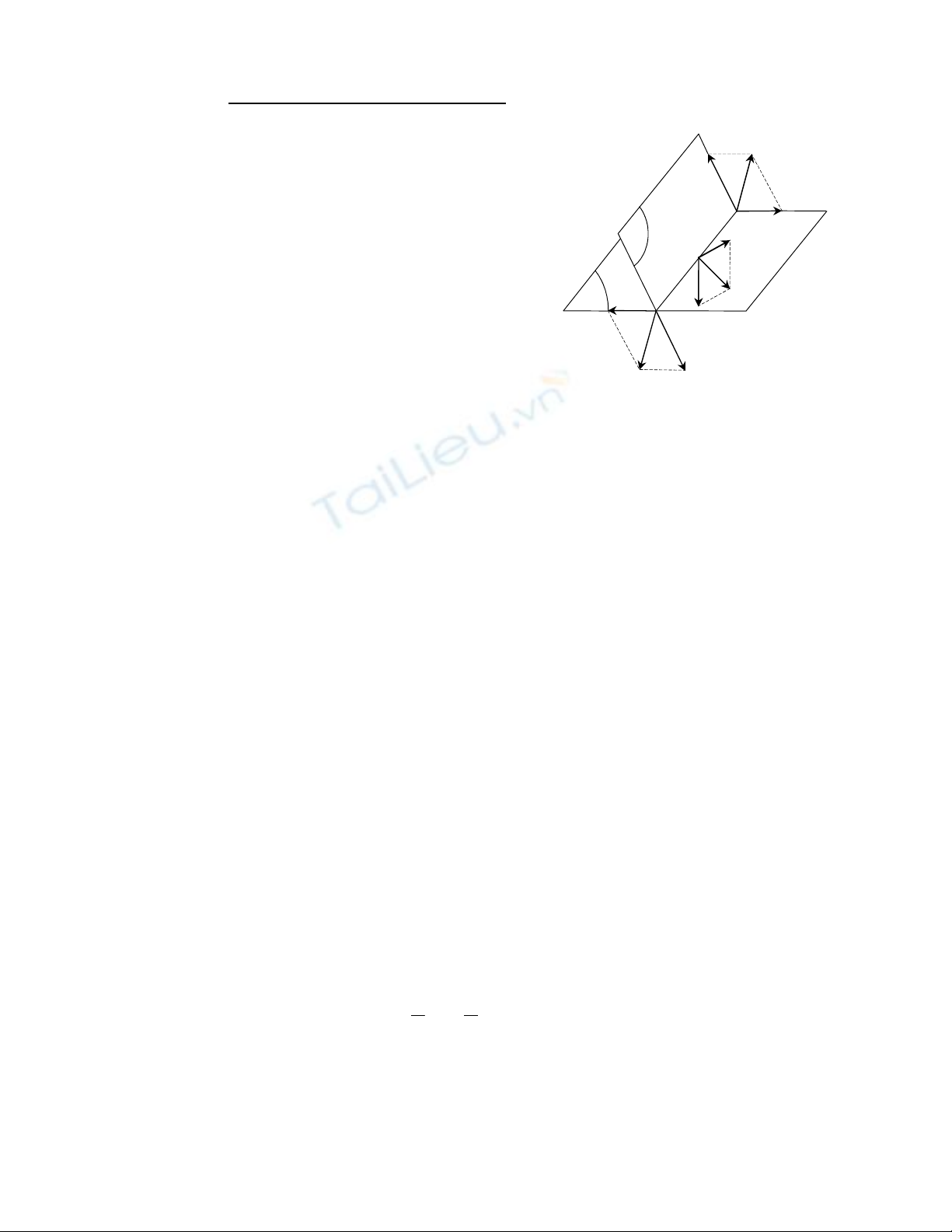
b. Định lý 2- Định lý về dời ngẫu lực theo mặt phẳng song song: Tác dụng của ngẫu lực
không thay đổi khi dời ngẫu lực đến những mặt phẳng song song.
Chứng minh: Giả sử ngẫu lực
(
)
F,F
′
uruur
∈ mặt phẳng π. Ta lấy mặt phẳng π1 song song
với mặt phẳng π. Trên mặt phẳng π1 chọn A1, B1 sao cho
11
AB
uuuuur
=
AB
uuur
⇒ ABB1A1 là hình
bình hành.
Gọi I là giao điểm của AB1 và A1B. Tại I ta đặt thêm hai lực cân bằng
Φ
ur
và
′
Φ
uur
sao
cho
Φ
ur
=
F
ur
⇒
(
)
F,F
′
uruur
≡
(
)
(
)
(
)
F,F,,F, vaø F,
′′′′
ΦΦ=ΦΦ
uruururuururuuruurur
.
Áp dụng định lý 1 ta được:
(
)
(
)
1
F,,F
′′
Φ≡Φ
uruuruur
với
1
F
′
uur
=
′
Φ
uur
=
F
′
uur
đặt tại B1.
(
)
(
)
1
F,,F
′′
Φ≡Φ
uururuurur
với
1
F
ur
=
Φ
ur
=
F
ur
đặt tại A1.
⇒
(
)
F,F
′
uruur
≡
(
)
1
,F
′
Φ
uur
và
(
)
1
,F
′
Φ
uurur
≡
(
)
11
,,F,F
′′
ΦΦ
uururuur
Ta có:
(
)
,0
′
ΦΦ≡
uur
⇒
(
)
F,F
′
uruur
≡
(
)
11
F,F
′
uruur
Như vậy ngẫu lực
(
)
11
F,F
′
uruur
chính là ngẫu lực
(
)
F,F
′
uruur
dời đến mặt phẳng π1.
Nhận xét:
- Vectơ mômen của ngẫu lực
m
uur
là vectơ tự do (có điểm đặt tự do).
- Tác dụng của ngẫu lực không thay đổi khi:
• Dời tuỳ ý ngẫu lực trong mặt phẳng tác dụng của nó.
• Dời đến các mặt song song.
• Thay đổi cánh tay đòn hoặc thay đổi giá trị của lực thành phần mà không
làm thay đổi giá trị của mômen ngẫu lực.
π
1
π
B
A
A1
B1 I
F
′
ur
F
r
F
r
1
F
′
ur
Φ
ur
′
Φ
uur
12
c. Định lý 3- Định lý về hợp ngẫu lực.
- Định lý về hợp hai ngẫu lực: Hợp hai ngẫu lực được một ngẫu lực có vectơ mômen
bằng tổng các vectơ mômen của hai ngẫu lực đã cho.
Chứng minh: Giả sử có hai ngẫu lực nằm
trong hai mặt phẳng π1 và π2 giao nhau theo giao
tuyến AB. Ta có thể biến đổi hai ngẫu lực trên thành
hai ngẫu lực
(
)
F,F
′
uruur
và
(
)
P,P
′
uruur
như hình vẽ có vectơ
mômen tương ứng
1
m
uur
,
2
m
uur
.
Rõ ràng
F
ur
và
F
′
uur
,
P
ur
và
P
′
uur
đối xứng qua tâm
I (trung điểm AB).
Theo tiên đề 3 ta có:
(
)
F,P
urur
≡
Φ
ur
và
(
)
F,P
′′
uuruur
≡
′
Φ
uur
⇒
(
)
F,F,P,P
′′
uruururuur
≡
(
)
,
′
ΦΦ
uruur
.
Do tính chất đối xứng nên
(
)
,
′
ΦΦ
uruur
cũng là một ngẫu lực.Ta có:
1
m
uur
=
BAF
∧
uuurur
,
2
m
uur
=
BAP
∧
uuurur
⇒
1
m
uur
+
2
m
uur
=
BAF
∧
uuurur
+
BAP
∧
uuurur
=
BA(FP)
∧+
uuururur
=
BA
∧Φ
uuurur
=
m
uur
.
Với
m
uur
là vectơ mômen ngẫu lực
(
)
,
′
ΦΦ
uruur
.
- Định lý về hợp hệ ngẫu lực: Hợp hệ ngẫu lực được một ngẫu lực có vectơ
mômen bằng tổng các vectơ mômen của các ngẫu lực đã cho.
n
i
i1
mm
=
=
∑
uuruur
(2.4)
Chứng minh: Giả sử ta có hệ ngẫu lực như sau:
(
)
(
)
(
)
1122nn
F,F,F,F,...,F,F
′′′
uruururuururuur
. Các
hệ ngẫu lực này có các vectơ mômen ngẫu lực tương ứng là
12n
m,m,...,m
uuruuruur
Theo định lý 3 ta có:
(
)
(
)
(
)
112211
F,F vaø F,FR,R
′′′
≡
uruururuururuur
⇔
121
mmm
′
+=
uuruuruur
.
(
)
(
)
(
)
113322
R,R vaø F,FR,R
′′′
≡
uruururuururuur
⇔
132
mmm
′′
+=
uuruuruur
()()
(
)
(
)
(
)
n2n2nn
R,R vaø F,FF,F
−−
′′
≡
uruururuururur
⇔
()
n2n
mmm
−
′′
+=
uuruuruur
…………………………………………………………………………………
(
)
(
)
(
)
(
)
1122nn
F,F +F,FF,FF,F
′′′′
++=
uruururuururuururuur
L ⇔
12n
mmmm
+++=
uuruuruuruur
L
Hệ quả: Khi các ngẫu lực có cùng chung mặt phẳng tác dụng thì:
n
i
i1
mm
=
=
∑
(2.5)
Như vậy hệ ngẫu lực phẳng tương đương với một ngẫu lực tổng hợp có mômen đại
số bằng tổng đại số của những mômen ngẫu lực đã cho.
π
2
π
1
B
A
P
ur
F
r
Φ
ur
P
′
uur
F
′
ur
′
Φ
uur
I
m
uur
2
m
uur
m
uur