13
CHƯƠNG 3: HỆ LỰC KHÔNG GIAN
I. VECTƠ CHÍNH VÀ MÔMEN CHÍNH CỦA HỆ LỰC KHÔNG GIAN.
1. Vectơ chính của hệ lực không gian.
a. Định nghĩa: Vectơ chính của hệ lực không gian, ký hiệu
′
uur
R
, là tổng hình học của
các vectơ biểu diễn các lực của hệ lực.
R
′
uur
=
12n
FFF
+++
L
=n
k
k1
F
=
∑
r
(3.1)
b. Phương pháp xác định:
- Phương pháp vẽ: Lấy điểm O bất kỳ trong không gian, lần lượt vẽ các vectơ
1
1
OAF
=
uuuurr
,
2
12
AAF
=
uuuuur r
,⋅⋅⋅ ,
()
n
n1
AAF
−
=
uuuuuuur r
=
n
F
uur
.
Đường gãy khúc
()
12n
n-1
OAA...AA
gọi là đa giác lực. Vectơ
n
OA
uuuur
=
R
′
uur
gọi là vectơ
khép kín của đa giác lực.
- Phương pháp giải tích (chiếu):
n
x1x2xnxkx
k1
n
y1y2ynyky
k1
n
z1z2znzkz
k1
RFFFF
RFFFF
RFFFF
=
=
=
′=+++=
′
=+++=
′
=+++=
∑
∑
∑
L
L
L
(3.2)
222
xyz
y
xz
RRRR
R
RR
Cos;Cos;Cos
RRR
′′′′
=++
′
′′
α=β=γ=
′′′
(3.3)
(3.4)
Với α,β,γ là các góc hợp bởi
R
′
uur
và các trục Ox, Oy, Oz.
2. Mômen chính của hệ lực không gian.
a. Định nghĩa: Mômen chính của hệ lực không gian đối với tâm O, ký hiệu
uur
O
M
, là
một vectơ bằng tổng hình học các vectơ mômen các lực thuộc hệ lực đối với tâm O.
()()
nn
O
Okk
k
k1k1
MmFrF
==
==∧
∑∑
uuruurrr
r
(3.5)
b. Phương pháp xác định:
- Phương pháp vẽ: Lấy điểm O bất kỳ trong không gian, lần lượt vẽ các vectơ :
1
OA
uuuur
=
O1
m
uur
=
(
)
O1
mF
uurr
,
12
AA
uuuuur
=
O2
m
uur
=
(
)
O2
mF
uurr
, ⋅⋅⋅ ,
n1n
AA
−
uuuuuuur
=
On
m
uur
=
(
)
On
mF
uurr
Đa giác
()
12n
n-1
OAA...AA
gọi là đa giác vectơ mômen
n
OA
uuuur
=
O
M
uur
gọi là vectơ khép
kín của đa giác.
- Phương pháp chiếu:
14
() ()
()
() ()
()
() ()
()
nnn
Ox
Oxkxk
kkzkky
k1k1k1
nnn
Oy
Oykyk
kkxkkz
k1k1k1
nnn
Oz
Ozkzk
kkykkx
k1k1k1
MmFmFyFzF
MmFmFzFxF
MmFmFxFyF
===
===
===
===−
===−
===−
∑∑∑
∑∑∑
∑∑∑
rr
rr
rr
(3.6)
Trong đó:
kkk
x,y,z
là toạ độ của điểm đặt lực
k
F
ur
.
kxkykz
F,F,F
là hình chiếu của
k
F
ur
trên các trục Ox, Oy, Oz.
()()()
222
O
OOO
M=MMM
MMM
C;C;C
MMM
++
αβγ
OxOyOz
OxOyOz
(3.7)
os=os=os= (3.8)
c. Định lý biến thiên mômen chính:
Định lý: Biến thiên mômen chính của hệ lực khi tâm lấy mômen thay đổi từ O đến O’
bằng mômen của vectơ chính đặt tại O lấy đối với điểm O’.
(
)
OO
OO
MMmR
′
′
′
−=
uuruuruuruur
(3.9)
Chứng minh:
Ta có:
()()
nn
O
Okk
k
k1k1
MmFrF
′
′
==
′
==∧
∑∑
uuruurrr
r
()()
nn
O
Okk
k
k1k1
MmFrF
==
==∧
∑∑
uuruurrr
r
⇒
O
M
′
uur
-
O
M
uur
=
()
n
k
k
k1
rF
=
′
∧
∑
ur
r
-
()
n
k
k
k1
rF
=
∧
∑
ur
r
=
()
n
k
kk
k1
rrF
=

′
−∧

∑
r
rr
Ta có kk
rrOO
′′
−=
uuuur
rr
nên:
O
M
′
uur
-
O
M
uur
=
()
n
k
k1
OOF
=
′
∧
∑
uuuurr
=
()
n
k
k1
OOF
=
′
∧
∑
uuuurr
=
O
OOR
′′
∧
uuuuruur
=
(
)
OO
mR
′
′
uuruur
Nhận xét:
Trường hợp hệ lực đồng quy tại O ta có: O
M0
=
uur
⇒
(
)
O
O
M=mR
′
′
′
uuruuruur
(3.10)
Trường hợp hệ lực phẳng:
()
n
O
Ok
k1
MmF
=
=
∑
r
(3.11)
II.THU GỌN HỆ LỰC KHÔNG GIAN.
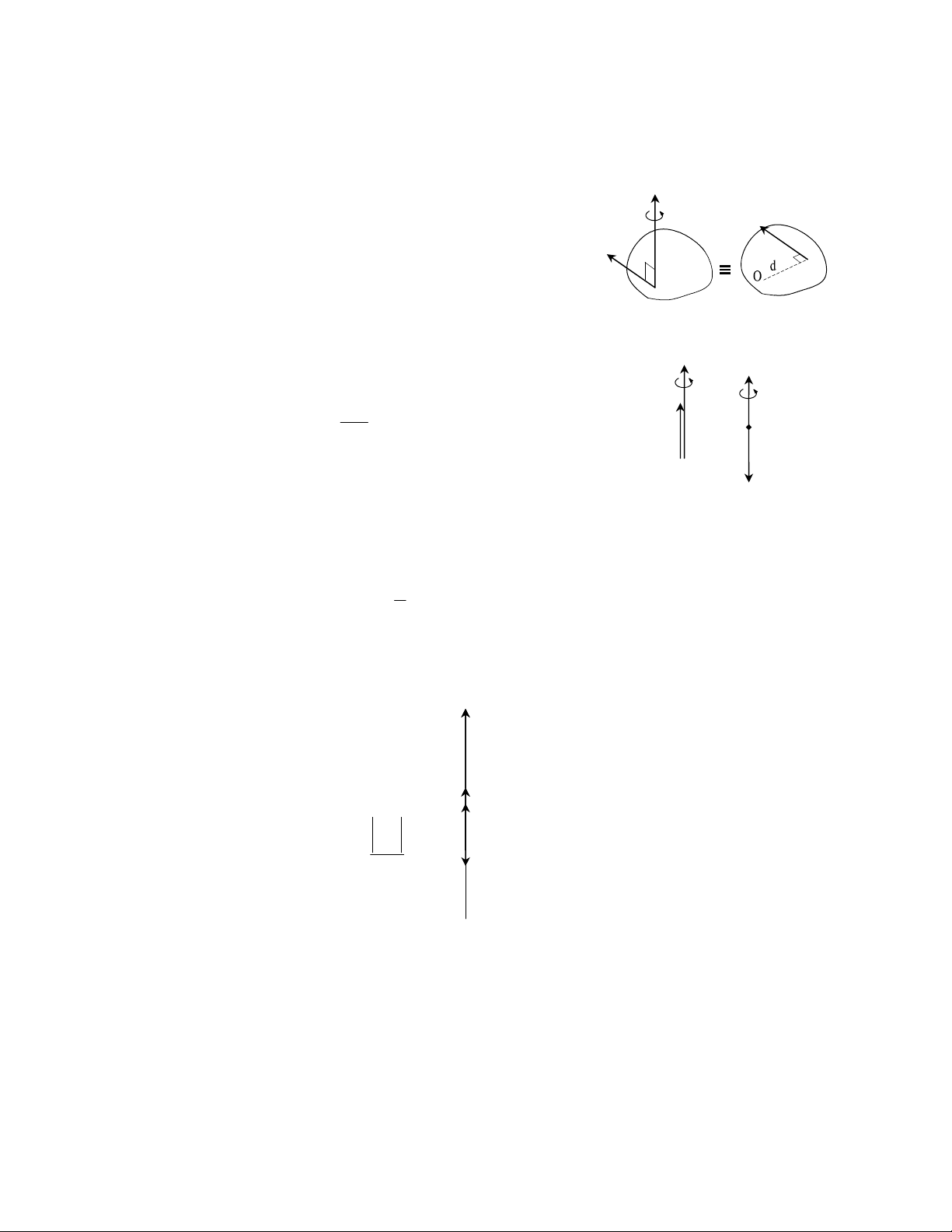
1. Định lý dời lực song song.
Định lý: Lực
ur
F
đặt tại A tương đương với lực
′
uur
F
song song, cùng chiều, cùng cường
độ với lực
ur
F
nhưng đặt tại O và một ngẫu lực có mômen bằng mômen của lực
ur
F
lấy đối với
điểm O.
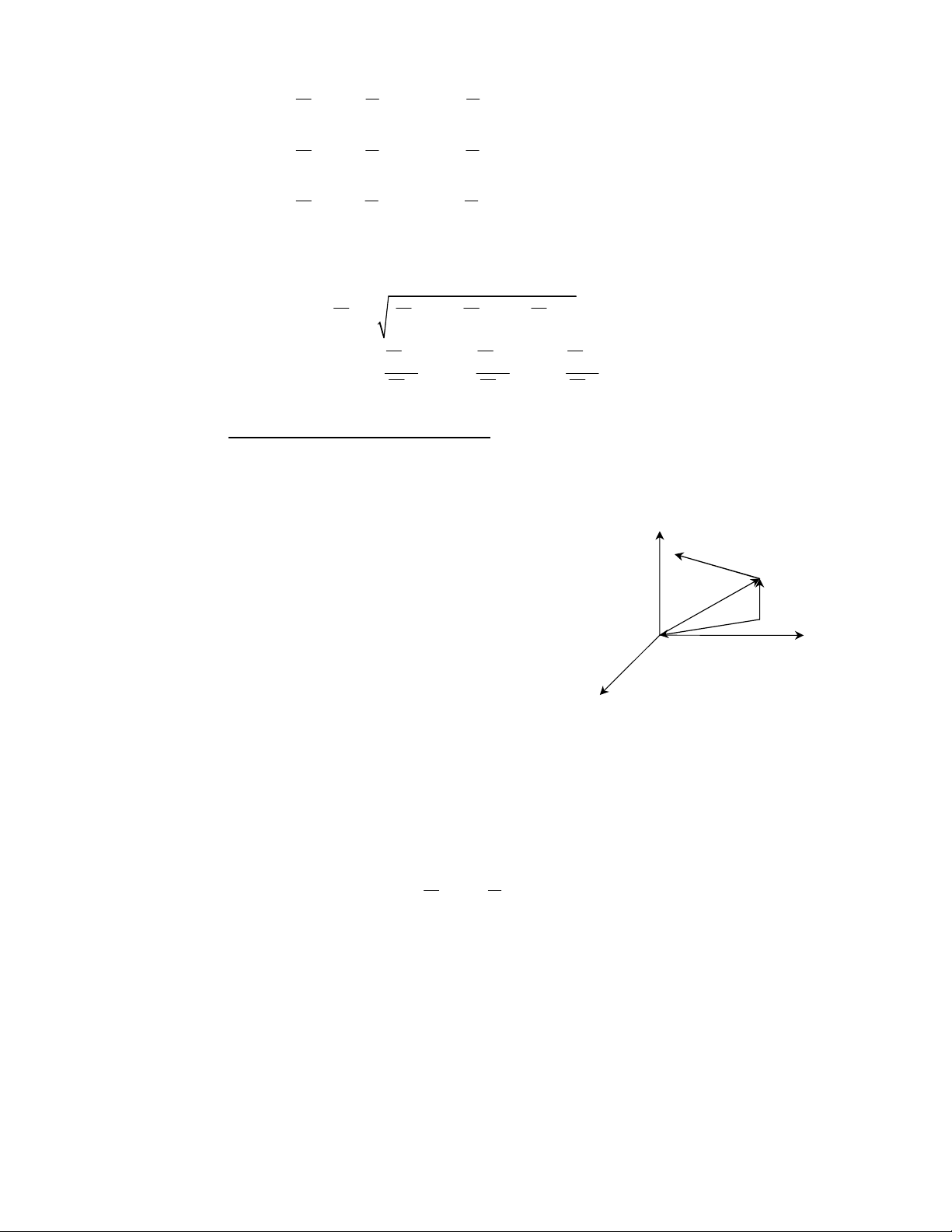
Chứng minh:
O O’
k
r
r
k
r
′
r
k
F
r
Z
Y
X
15
Đặt tại O hai lực
F
′
uur
và
F
′′
uur
với
(
)
F,F0
′′′
≡
uuruur
và
F
ur
=
F
′
uur
⇒
(
)
F
ur
≡
(
)
F,F,F
′′′
uruuruur
≡
F
′
uur
và
(
)
F,F
′′
uruur
⇒
(
)
F
ur
≡
F
′
uur
và
(
)
O
mF
uurur
.
Nhận xét:
Nhận thấy
M
uur
=
(
)
O
mFF
⊥
uurrr
.
⇒ Hệ lực gồm một lực
F
′
uur
và một vectơ mômen
M
uur
vuông góc với
F
′
uur
sẽ tương đương với một lực
F
ur
cách
F
′
uur
một đoạn
M
d
F
=. Điểm đặt của lực
F
ur
phụ thuộc vào chiều của
M
uur
.
2. Thu gọn hệ lực không gian về tâm.
Định lý: Hệ lực không gian bất kỳ tương đương với một lực và một ngẫu lực đặt tại
một điểm tuỳ ý, chúng được gọi là lực thu gọn và ngẫu lực thu gọn. Lực thu gọn được biểu
diễn bằng vectơ chính của hệ lực đặt tại tâm thu gọn, còn ngẫu lực thu gọn có vectơ
mômen bằng mômen chính của hệ lực đối với tâm thu gọn.
Chứng minh:
Lần lượt dời các lực
12n
F,F,...,F
rrr
về tâm tâm thu gọn (giả sử là O).
(
)
()
()
111O1
222O2
nnnOn
FF vaø mmF
FF vaø mmF
........................................
..
FF vaø mmF
′
≡=
′
≡=
′
≡=
uruuruuruurur
uruuruuruurur
uruuruuruurur
Cộng từng vế ta được:
(
)
(
)
(
)
12n12n12n
,,...,,,...,m,m,...,m
FFFFFF vaø
′′′
=
urururuuruuruuruuruuruur
Vì
(
)
12n
,,...,
FFF
′′′
uuruuruur
là hệ lực đồng quy tại O nên:
(
)
12n
,,...,
FFF
′′′
uuruuruur
≡
O
R
′
uur
=n
k
k1
F
=
′
∑
ur
=n
k
k1
F
=
∑
r
=
R
′
uur
.
Và
(
)
12n
m,m,...,m
uuruuruur
=
O
M
uur
=
()
n
Ok
k1
mF
=
∑
uurr
Vậy khi thu gọn hệ lực không gian về O ta được:
()
n
Ok
k1
n
O
Ok
k1
RFR
MmF
=
=
′′
==
=
∑
∑
uurruur
uuruurr
(3.12)
3. Các bất biến của hệ lực không gian.
Từ (3.12). Ta có: O
RRConst
′
==
uruur
(3.13)
Đây là bất biến thứ nhất của hệ lực không gian. Mặt khác theo định lý biến thiên
mômen chính khi thay đổi tâm thu gọn ta có:
(
)
OO
OO
MMmR
′
′
′
−=
uuruuruuruur
, nhân hai vế với
O
R
ur
ta
được:
O
M
′
uur
.
O
R
ur
–
O
M
uur
.
O
R
ur
=
(
)
OO
mR
′
′
uuruur
.
O
R
uuur
. Mà
(
)
OO
mR
′
′
uuruur
⊥
O
R
ur
⇒
(
)
OO
mR
′
′
uuruur
.
O
R
ur
= 0
nên:
Thay vào ta có
O
M
′
uur
.
O
R
ur
–
O
M
uur
.
O
R
ur
= 0 hay
O
M
′
uur
.
O
R
ur
=
O
M
uur
.
O
R
ur
= const. (3.14)
O A
(
)
O
mF
uurr
F
r
F
′
ur
F
′′
uur
16
Đây là bất biến thứ hai của hệ lực không gian: “Tích vô hướng của mômen thu gọn và
lực thu gọn của hệ lực không gian là một hằng số”. Hay “Hình chiếu của mômen thu gọn
lên lực thu gọn là một hằng số”
* Các trường hợp xảy ra:
1.
O
R
′
uur
= 0,
O
M
uur
= 0 ⇔ hệ lực không gian cân
bằng
2.
O
R
′
uur
= 0,
O
M
uur
≠ 0 ⇔ hệ lực không gian
tương đương với một ngẫu lực tại O.
3.
O
R
′
uur
≠ 0,
O
M
uur
= 0 ⇔ hệ lực không gian
tương đương với một hợp lực đặt tại O.
4.
O
R
′
uur
≠ 0,
O
M
uur
≠ 0
a)
O
R
′
uur
⊥
O
M
uur
⇔ Hệ lực không gian tương
đương với một hợp lực
R
ur
bằng vectơ chính
R
′
uur
và
cách O một đoạn
O
O
M
d
R
=
′
.
b)
O
R
′
uur
//
O
M
uur
:
O
R
′
uur
↑↑
O
M
uur
⇔ Hệ lực không gian
tương đương với hệ xoắn thuận.
O
R
′
uur
↑↓
O
M
uur
⇔ Hệ lực không gian
tương đương với hệ xoắn ngược.
c)
(
)
O
O
R,M
′
uuruur
=
2
π
α≠
⇒ Hệ lực không gian tương đương một hệ xoắn nhưng
trục xoắn không đi qua tâm thu gọn.
Chứng minh:
Phân tích
OOO
12
MMM
=+
uuruuruur
(
)
O
O
R,M
′
⇒
uuruur
≡
(
)
OO
O21
R,M vaø M
′
uuruuruur
Theo trường hợp đầu tiên ta
có:
(
)
O
O2
R,M
′
uuruur
≡
O1
R
′
uur
với
O1
R
′
uur
có điểm
đặt cách O một đoạn
O
2
M
d
R
=
′
uur
.
Vậy
(
)
O
O
R,M
′
uuruur
≡
(
)
O
1O1
M,R
′
uuruur
.
Rõ ràng đây là một hệ xoắn và
trục xoắn không đi qua tâm thu gọn O mà đi qua O1 cách O một khoảng d.
III. CÁC KẾT QUẢ KHI THU GỌN HỆ LỰC KHÔNG GIAN VỀ TÂM THU GỌN
(CÁC DẠNG TỐI GIẢN CỦA HỆ LỰC KHÔNG GIAN)
1. Định lý Varinhông.
Nếu hệ lực không gian có hợp lực thì mômen của hợp lực đối với một tâm bất kỳ
bằng tổng mômen của các lực thành phần đối với tâm ấy.
Trường hợp a
O
MM
=
uuruur
O
RR
=
urur
O
R
ur
Trường hợp b
O
MM
=
uuruur
O
O
RR
=
urur
O
MM
=
uuruur
O
RR
=
urur
O
Hệ xoắn
thuận
Hệ xoắn
ngược
O
RR
′
=
uurur
O
O
M
uur
O
1
M
uur
O
2
M
uur
O
d
O
1
M
uur
O1
RR
′
=
uurur
O1
17
()()
n
OOk
k1
mRmF
=
=
∑
uururuur r
. (3.15)
Chứng minh: Giả sử hệ lực không gian có hợp lực
R
ur
. Gọi O1
là điểm nằm trên đường tác dụng của
R
ur
. Theo định lý biến thiên
mômen chính ta có:
(
)
OO1
OO1
MMmR
′
−=
uuruuruuruur
.
Dễ dàng thấy
O
M
uur
= 0 nên
O
M
uur
=
(
)
OO1
mR
′
uuruur
. Mặc khác
O1
R
′
uur
=
R
ur
⇒
O
M
uur
=
(
)
OO1
mR
′
uuruur
=
()
n
Ok
k1
mF
=
∑
uurr
. (ĐPCM)
2. Các dạng chuẩn của hệ lực không gian.
1.
R
′
uur
= 0,
O
M
uur
= 0: Hệ lực không gian cân bằng
2.
R
′
uur
= 0,
O
M
uur
≠ 0: Hệ lực không gian tương đương với một ngẫu lực (không phụ
thuộc vào tâm thu gọn).
3.
R
′
uur
≠ 0,
O
M
uur
= 0: Hệ lực không gian tương đương với một hợp lực.
4.
O
R
′
uuur
≠ 0,
O
M
uur
≠ 0
a)
O
R
′
uuur
⊥
O
M
uur
: Hệ lực không gian tương đương với một hợp lực
R
ur
bằng vectơ
chính
R
′
uur
và cách O một đoạn
O
O
M
d
R
=
′
b)
O
R
′
uuur
//
O
M
uur
: Hệ lực không gian tương đương với một hệ xoắn.
c) (
O
R
′
uuur
,
O
M
uur
) =
2
π
α≠
: Hệ lực không gian tương đương một hệ xoắn nhưng trục
xoắn không đi qua tâm thu gọn.
IV. CÁC DẠNG TỐI GIẢN CỦA CÁC HỆ LỰC ĐẶC BIỆT.
1. Hệ lực đồng quy.
Vì
()
n
O
Ok
k1
MmF
=
=
∑
uuruurr
=0 ⇒
R0
R0
′
=
′
≠
uur
uur ⇔
Heä löïc ñoàng quy caân baèng
Heä löïc ñoàng quy coù hôïp löïc
2. Hệ ngẫu lực.
Vì n
k
k1
RF0
=
′
==
∑
uurr
nên ⇒
O
O
M0
M0
=
≠
uur
uur ⇔ Heä ngaãu löïc caân baèng
Heä ngaãu löïc töông ñöông vôùi moät nga
ãu löïc.
3. Hệ lực song song.
Vì n
k
k
k1
FR//F
=
′
=
∑
uuruurr
⇒
()
n
O
Ok
k1
MmFR
=
′
=⊥
∑
uuruurruur
.
⇒
()
O
O
O
OO
M0,R0
M0,R0
M0,R0
M0,R0;MR
′
==
′
≠=
′
=≠
′′
≠≠⊥
uuruur
uuruur
uuruur
uuruuruuruur
⇔
Heä caân baèng
Heä coù ngaãu löïc
Heä coù hôïp löïc
Heä coù hôïp löïc khoâng ñi qua taâm thu
goïn
O
MM
=
uuruur
R
ur
O
1
O
O1
R
′
uur