31
CHƯƠNG 5: TRỌNG TÂM
I. TÂM CỦA HỆ LỰC SONG SONG.
1 Định lý về hợp lực hệ lực song song.
Trường hợp hệ lực song có hợp lực, nếu giữ nguyên điểm đặt, cường độ và quan hệ
song song giữa các lực thành phần nhưng thay đổi phương chung của chúng một cách tuỳ
ý, thì hợp lực cũng thay đổi phương theo nhưng luôn đi qua một điểm C cố định. Điểm C
đó được gọi là tâm hệ lực song
song.
Chứng minh:
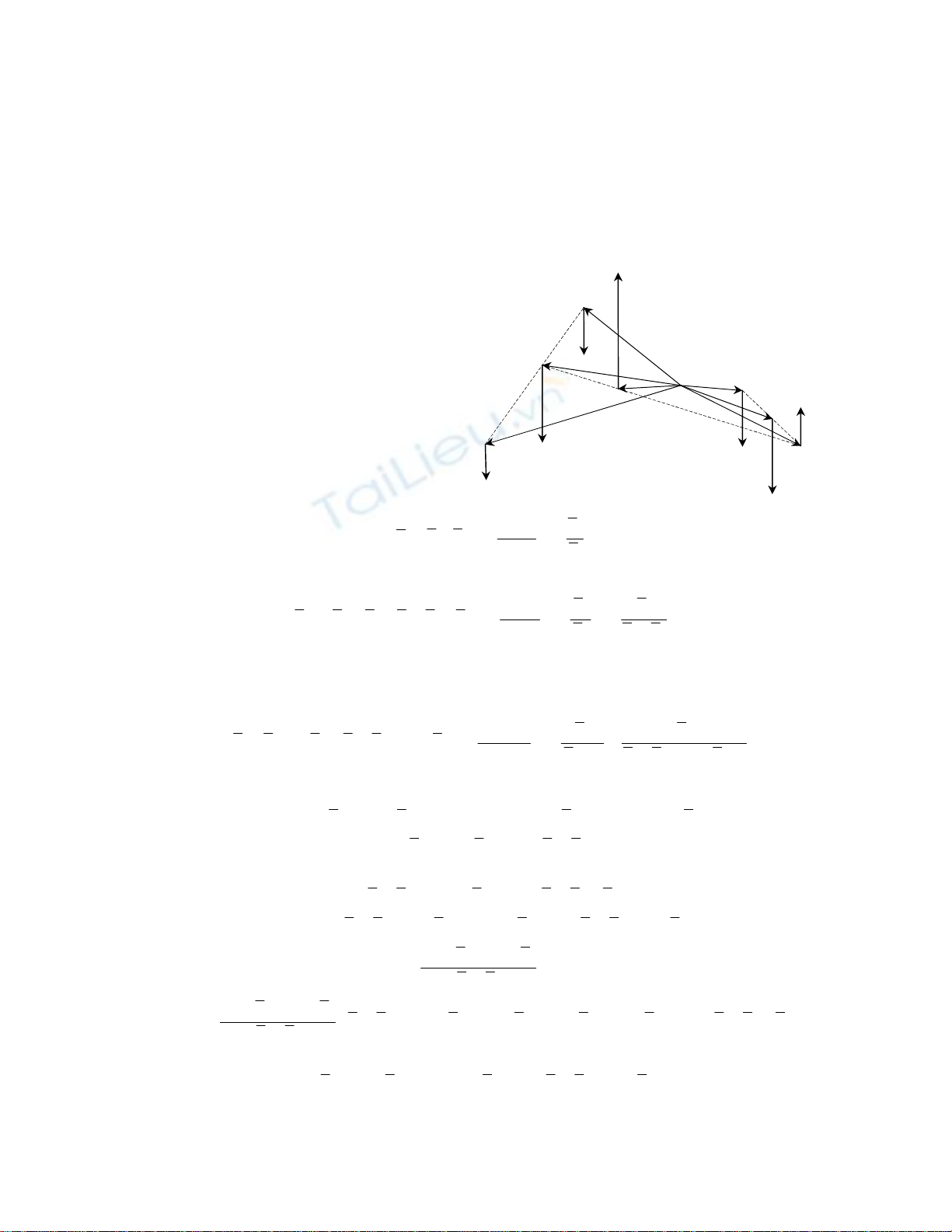
Xét hệ lực song song bất kỳ
(
)
12n
,,...,
FFF
ururur
trong không gian,
đặt tại các điểm tương ứng
12n
A,A,...,A
.
Ta lần lượt hợp các lực không
tạo thành ngẫu lực từng đôi một.
Hợp lực
F
r
và
2
F
ur
ta được
1
R
ur
đặt tại C1 nằm trên A1,A2.
R
=
1
F
+
2
F
và
112
1
12
CAF
F
CA
=−
uuuuur
uuuuur (a).
Tiếp tục hợp
1
R
ur
và
1
F
ur
ta được
2
R
ur
đặt tại C2 nằm trên C1A3. Với :
213123
RRFFFF
=+=++
và 3321
112
23
FF
CC
RFF
CA =−=−
+
uuuuur
uuuuur (b)
Tiếp tục hợp lần lượt các lực ta được
()
n2
R
−
ur
đặt tại
()
n2
C
−
. Tiếp tục hợp lực này với
n
F
ur
ta được hợp lực
R
ur
của hệ đặt tại điểm C thuộc
()
n
n2
CA
−với :
n2n12n
RRFFFF
−
=+=+++
L
và
()
() ()
n2 nn
12
n2n1
n
CC FF
RFFF
CA
−
−−
=−=
+++
uuuuuuur
uuuur L (c)
Gọi
K
OA
uuuuur
là vectơ định vị điểm AK và
OC
uuur
là vectơ định vị điểm C. Từ (a) ta có:
111122
CA.FCA.F0
+=
uuuuuruuuuur
⇔ 111212
(OAOC).F(OAOC).F0
−+−=
uuuuruuuuruuuuruuuur
⇔
1122112
OA.FOA.FOC(FF)
+=+
uuuuruuuuruuuur
(a’)
Biến đổi (b), (c) tương tự ta cũng được :
11233212.3
OC(FF)OA.FOC(FFF)
++=++
uuuuruuuuruuuur
(b’)
n212n1nn12n
OC.(FFF)OA.FOC(FFF)
−−
++++=+++
uuuuuuruuuuruuur
LL
(c’)
Biến đổi (a’) thành:
1122
112
OA.FOA.F
OC FF
+
=+
uuuuruuuur
uuuur
thay vào (b’) ta được:
1122
1233112233212.3
12
OA.FOA.F
.(FF)OA.FOA.FOA.FOA.FOC(FFF)
FF
+++=++=++
+
uuuuruuuur
uuuuruuuuruuuuruuuuruuuur
Tiếp tục biến đổi tương tự ta được:
1122nn12.n
OA.FOA.FOA.FOC(FFF)
+++=+++
uuuuruuuuruuuuruuur
LL
(5.1)
A1
A2
C1
A3
C
2
An
C
1
F
r
2
F
r
3
F
r
n
F
r
1
R
ur
2
R
ur
R
ur
32
Rõ ràng vị trí điểm C không phụ thuộc vào phương chung của các vectơ thành phần
mà chỉ phụ thuộc giá trị đại số của các lực và điểm đặt của chúng. Như vậy định lý đã được
chứng minh.
2 Tâm hệ lực song song.
Từ (5.1) ta rút ra:
n
kk
k1n
k
k1
OA.F
OC
F
=
=
=∑
∑
uuuur
uuur .
Nếu gọi
K
r
r
là vectơ định vị điểm AK và
C
r
r
là vectơ định vị điểm C thì : Điểm hình học C
được gọi là tâm của hệ lực song song được xác định theo công thức:
n
k
k
k1
Cn
k
k1
F.r
r
F
=
=
=∑
∑
r
r (5.2).
Chiếu lên các phương ta được:
kkkkkk
kkk
CCC
kkk
kkk
x.Fy.Fz.F
x;y;z
FFF
===
∑∑∑
∑∑∑
(5.3)
II. TRỌNG TÂM CỦA VẬT RẮN.
1. Định nghĩa trọng tâm của vật.
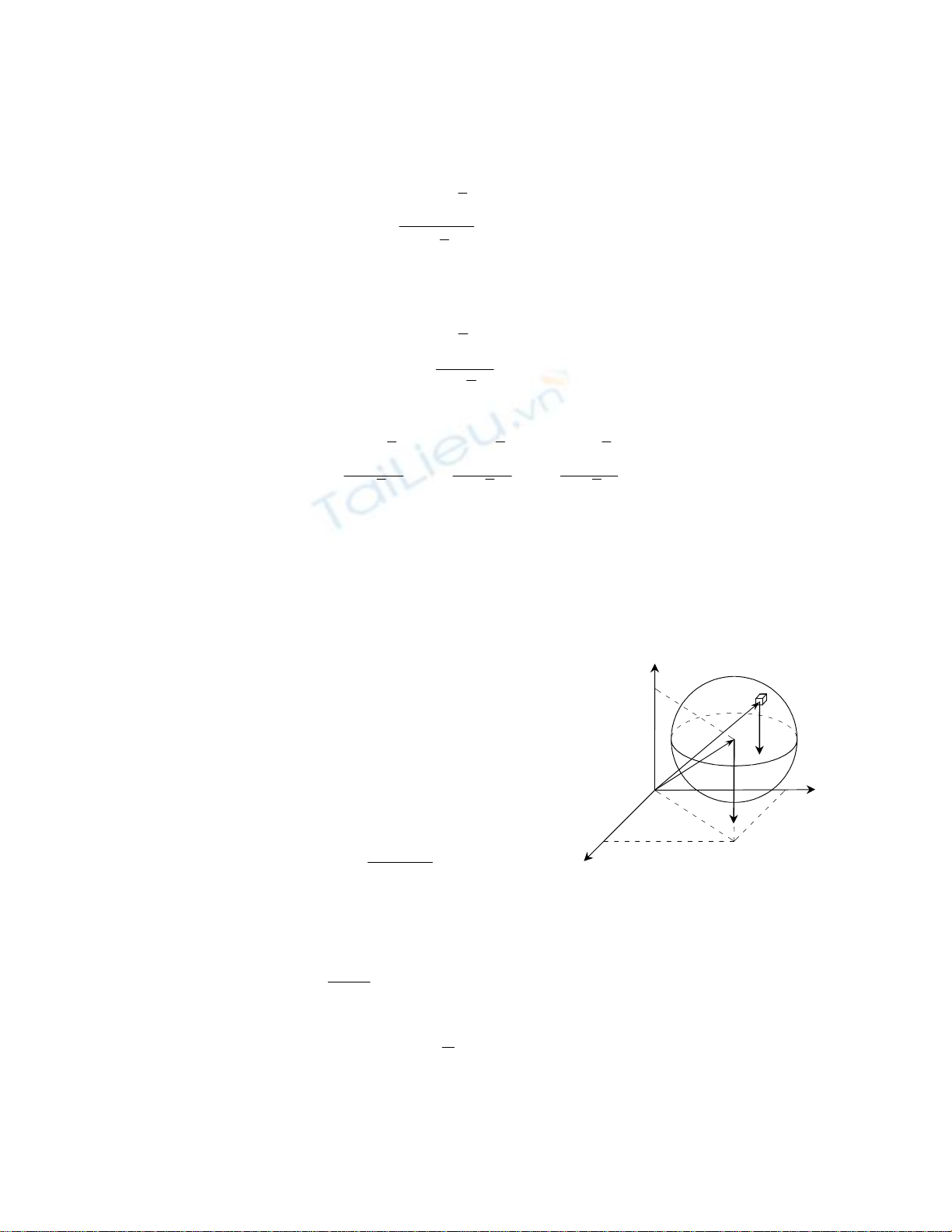
Khảo sát vật rắn nằm gần mặt đất chịu tác dụng của trọng lực
P
ur
hướng về tâm quả
đất. Chia vật rắn thành nhiều phần tử nhỏ. Mỗi phần tử chịu lực hút của quả đất (trọng lực
hướng về tâm quả đất).
Vì khoảng cách từ mỗi phần tử đến tâm quả
đất rất lớn nên có thể coi hệ các trọng lực là hệ lực
song song cùng chiều, giá trị của trọng lực được
gọi là trọng lượng của phần tử.
Ký hiệu Mk
là một điểm nào đó thuộc phần
tử thứ k, nó có trọng lượng ∆Pk và
k
r
r
là vectơ định
vị của điểm Mk.
Từ (5.2) ta có:
n
kk
k1
Cn
k
k1
P.r
r
P
=
=
∆
=
∆
∑
∑
r
r (5.4)
Theo toán học khi n→ ∞ thì
C
rr
→
rr
và k
PP
∆→
∑
. Khi đó C được gọi là trọng tâm
của vật rắn và: V
C
r.dP
r
P
=
∫
r
r
Định nghĩa :Trọng tâm của vật là điểm hình học được xác định bằng công thức:
C
V
1
rr.dP
P
=
∫
rr
(5.5)
2. Các công thức xác định trọng tâm của vật.
Chiếu (5.5) lên 3 trục toạ độ ta được:
x
y
z
C
xC
yC
zC Mk
k
P
∆
ur
P
ur
O
C
r
r
k
r
r
33
C
V
1
xx.dP
P
=
∫
; C
V
1
yy.dP
P
=
∫
; C
V
1
zz.dP
P
=
∫
(5.6)
(5.5) và (5.6) gọi là các công thức xác định trọng tâm của vật.
III. TRỌNG TÂM CÁC VẬT ĐỒNG CHẤT:
1. Khối đồng chất:
Một khối được gọi là đồng chất nếu thoả mãn: dP
conts
dV
ρ== ⇒ dP=ρ.dV⇒ P=ρ.V.
Với ρ gọi là trọng lượng riêng của vật
Khi đó: C
V
1
rr..dV
P
=ρ
∫∫∫
rr
= C
V
rr.dV
.V
ρ
=ρ
∫∫∫
rr
=
V
1
r.dV
V
∫∫∫
r
(5.7)
Hoặc C
V
1
xx.dV
V
=
∫∫∫
; C
V
1
yy.dV
V
=
∫∫∫
; C
V
1
zz.dV
V
=
∫∫∫
(5.8)
2. Mặt đồng chất (tấm đồng chất):
Một tấm (mặt) được gọi là đồng chất nếu thoả mãn: dP
conts
dS
ρ== ⇒ dP=ρ.dS⇒
P=ρ.S.
Khi đó: C
S
1
rr.dS
S
=
∫∫
rr
(5.9), hoặc: C
S
1
xx.dS
S
=
∫∫
; C
S
1
yy.dS
S
=
∫∫
;C
S
1
zz.dS
S
=
∫∫
(5.10)
3. Thanh, đường đồng chất:
Một đường (thanh) gọi là đồng chất nếu thoả mãn: dP
const
dL
ρ== ⇒ dP=ρ.dL⇒
P=ρ.L.
Khi đó: C
L
1
rr.dL
L
=
∫
rr
(5.11), hoặc: C
L
1
xx.dL
L
=
∫
; C
L
1
yy.dL
L
=
∫
;C
L
1
zz.dL
L
=
∫
(5.12)
IV: CÁC PP XÁC ĐỊNH TT CỦA VẬT VÀ CÁC ĐỊNH LÝ LIÊN QUAN.
1. Phương pháp đối xứng.
Định lý 1: Nếu vật rắn đồng chất có tâm (trục, mặt phẳng) đối xứng thì trọng tâm
của nó nằm tại tâm (trục, mặt phẳng) đối xứng.
Chứng minh: Xét vật có tâm đối xứng O, đồng chất. ứng với phần tử MK có trọng
lượng ∆PK và vectơ định vị
K
r
r
thì có phần tử
K
M
′
có trọng lượng ∆PK đối xứng qua tâm O,
tức vectơ định vị của nó là
k
r
−
r
. Phân hoạch vật rắn thành từng cặp phần tử đối xứng qua
tâm và tính tổng.
(
)
kkkk
C
P.rPr
r0
P
∆+∆−
==
∑∑
rr
r (đpcm)
Xét vật có trục đối xứng, chọn Oz làm trục đối xứng. Khi đó ứng với mỗi điểm MK
có toạ độ xK, yK và trọng lượng ∆PK thì có điểm
K
M
′
có toạ độ -xK, -yK và trọng lượng ∆PK
34
⇒
(
)
()
kkkk
kk
C
kkkk
kk
C
x.Px.P
x0
P
y.Py.P
y0
P
∆+−∆
==
∆+−∆
==
∑∑
∑∑ ⇒ C nằm trên trục Oz là trục đối xứng
Định lý 2:Nếu vật rắn gồm các phần mà trọng tâm của các phần đó nằm trên một
đường thẳng ( mặt phẳng) thì trọng tâm của vật cũng nằm trên đường thẳng (mặt phẳng)
đó.
Chứng minh: Giả thiết vật rắn gồm n phần có trọng lượng là
12n
P,P,...,P
và có trọng
tâm tương ứng là
12n
C,C,...,C
. Trọng tâm của cả vật khảo sát là tâm của hệ lực song song
(
)
12n
,,...,
PPP
ururur
nghĩa là:
⇔
n
Ckk
k1
1
xx.P
P=
=∑; n
Ckk
k1
1
yy.P
P=
=∑; n
Ckk
k1
1
zz.P
P=
=∑ (1)
Nếu
12n
C,C,...,C
thuộc đường thẳng ∆ thì chọn đường thẳng ∆ đó làm trục Oz. Khi
đó xk=0, yk= 0 thay vào (1) ta có xC = 0, yC= 0. Như vậy điểm C cũng thuộc trục Oz hay C
thuộc ∆.
Tương tự nếu Ci thuộc mặt phẳng π thì ta chọn π làm mặt phẳng Oxy ⇒ zi = 0. Thay
vào (1) ta có zC = 0. Như vậy điểm C thuộc mặt phẳng π.
2. Phương pháp phân chia thêm bớt.
Định lý 1: (Định lý phân chia thêm bớt, vật ghép)
Nếu vật rắn được ghép từ m phần, mỗi phần có trọng lượng P
i
và trọng tâm C
i
(xi,yi,zi) thì trọng tâm của vật được xác định nhờ công thức:
m
ii
i1
Cm
i
i1
P.x
x
P
=
=
=∑
∑
;
m
ii
i1
Cm
i
i1
P.y
y
P
=
=
=∑
∑
;
m
ii
i1
Cm
i
i1
P.z
z
P
=
=
=∑
∑
(5.13)
Chứng minh: Trọng tâm của vật rắn là tâm của hệ lực song song
12m
P,P,...,P
. Từ
(5.3) ta có (5.13)
Xét trường hợp vật rắn bị khuyết. Khi đó công thức trên vẫn đúng vì phần khuyết
được xem như là phần ghép có trọng lượng âm.
3. Phương pháp tích phân.
Xác định qui luật biến thiên của trọng tâm từng phần tử khi phân hoạch. Kết hợp với
đổi biến số của tích phân ta dùng các công thức (5.7), (5.8),..., (5.12) để tìm trọng tâm của
vật.
4. Phương pháp quay – định lý GuynĐanh. (Tham khảo).
5. Phương pháp thực nghiệm.
Phương pháp cân
Phương pháp treo
Phương pháp tâm lắc.
V: TRỌNG TÂM CỦA MỘT SỐ VẬT ĐƠN GIẢN.
1. Thanh đồng chất.
Áp dụng định lý 1 của phương pháp đối xứng ta dễ dàng nhận thấy trọng tâm của
thanh đồng chất là điểm giữa của thanh.
35
2. Các vật có dạng hình học cơ bản.
Áp dụng phương pháp đối xứng ta dễ dàng nhận thấy trọng tâm của hình bình hành,
chữ nhật, hình vuông, khối hộp, khối chữ nhật, khối lập phương đồng chất chính là tâm
hình học của chúng.
3. Tam giác.
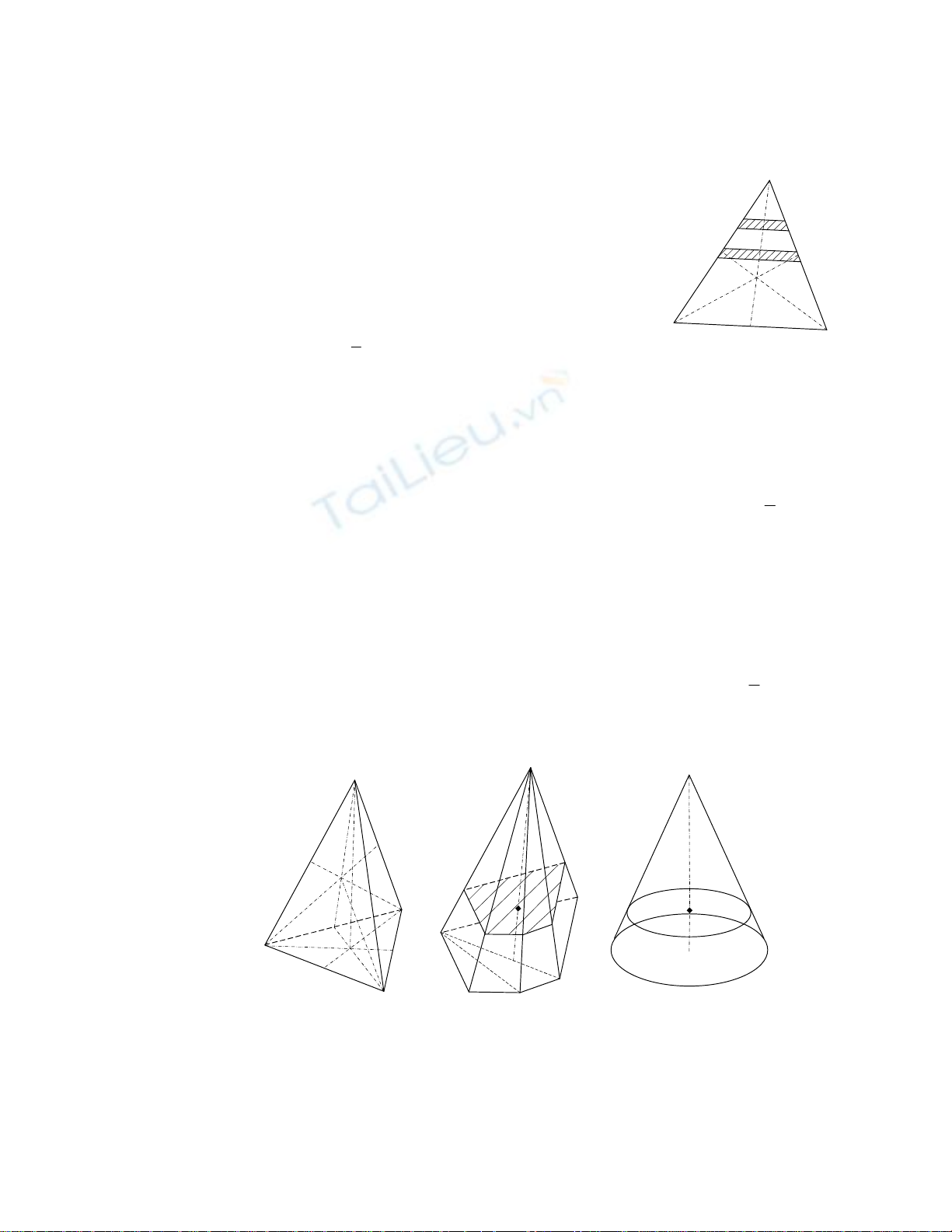
Chia tam giác thành các dải mỏng song song với đáy BC
của tam giác. Trọng tâm của mỗi dải nằm trên trung điểm của
nó tức sẽ nằm trên trung tuyến AM. Như vậy trọng tâm tam giác
nằm trên trung tuyến AM. Tương tự chia tam giác theo cạnh
đáy AC ta thấy trọng tâm tam giác phải nằm trên trung tuyến
BN. Như vậy trọng tâm tam giác chính là giao của 3 đường
trung tuyến. CM= 1
AM
3
.
3. Tứ diện.
Phân hoạch tứ diện SABD thành những lát vô cùng mỏng hình tam giác song song với
đáy ABD. Trọng tâm mỗi tam giác nằm tại giao của các đường trung tuyến. Do vậy trọng tâm
của tứ diện nằm trên đường SM là đường nối đỉnh tứ diện và trọng tâm đáy tam giác. Tương tự
ta cũng chứng minh được trọng tâm tứ diện cũng phải nằm trên đoạn BN. Như vậytrọng tâm tứ
diện là giao của hai đường SM, BN. Theo hình học ta có công thức: CM= 1
SM
4
.
4. Hình chóp
Với hình chóp đáy là đa giác ta có thể phân đa giác này thành các tam giác. Trọng
tâm của các tứ diên này nằm trên một mặt phẳng song song với đáy và khoảng cách từ mặt
phẳng này đến đỉnh chóp gấp 3 lần khoảng cách đến đáy. Cũng có thể phân hoạch hình
chóp thành các lát mỏng song song với đáy, như vậy trọng tâm hình chóp phải nằm trên
đường nối giữa đỉnh chóp và trọng tâm đáy đa giác. Kết hợp hai phân tích trên ta có trọng
tâm hình chóp nằm trên đường nối đỉnh chóp S với trọng tâm của đáy M. CM= 1
SM
4
.
Với hình chóp đáy là đường cong khép kín ta có thể coi đó là đa giác khi số cạnh
tiến đến vô cùng và ta cũng nhận được kết quả tương tự.
S
D
B
A
N
M
C
S
A
B D E
F
M
C C
M
S
A
D
C
M
N