DAÏNG ÑEÀ THI HSG M«n thi TO¸N CAÁP HUYEÄN
Thêi gian lµm bµi 150 phót, kh«ng kÓ thêi gian giao ®Ò
Câu 1. ( 2,5 đi m) Cho bi u th c ể ể ứ
1 x 1 x 1
P = x x x x x
� �
� �� �
� �� �
� �� �
− −
− − +
:
.
a) Tìm x ñeå P xaùc ñònh, rút g n P. ọ
b) Tính giá tr c a P khi ị ủ
2
x = 2 3+
.
c) Tìm giá tr c a x th a mãn đng th c ị ủ ỏ ẳ ứ
P. x 6 x 3 x 4= − − −
.
Câu 2. ( 2,0 đi mể)
a) Cho a + b + c = 0 và a, b, c khác 0. Ch ng minh r ng: ứ ằ
2 2 2
1 1 1 1 1 1
a b c
a b c
+ + = + +
b) Gi i ph ng trình ả ươ
x 7 x 5 2+ − − =
.
Câu 3. ( 1,5 điểm)
a) Tìm giá tr l n nh t và nh nh t c a bi u th c ị ớ ấ ỏ ấ ủ ể ứ
A = x 2 6 x− + −
b) Cho x và y th a mãn ỏ
( ) ( )
2 2
x x 2011 y y 2011 2011+ + + + =
. Tính x + y.
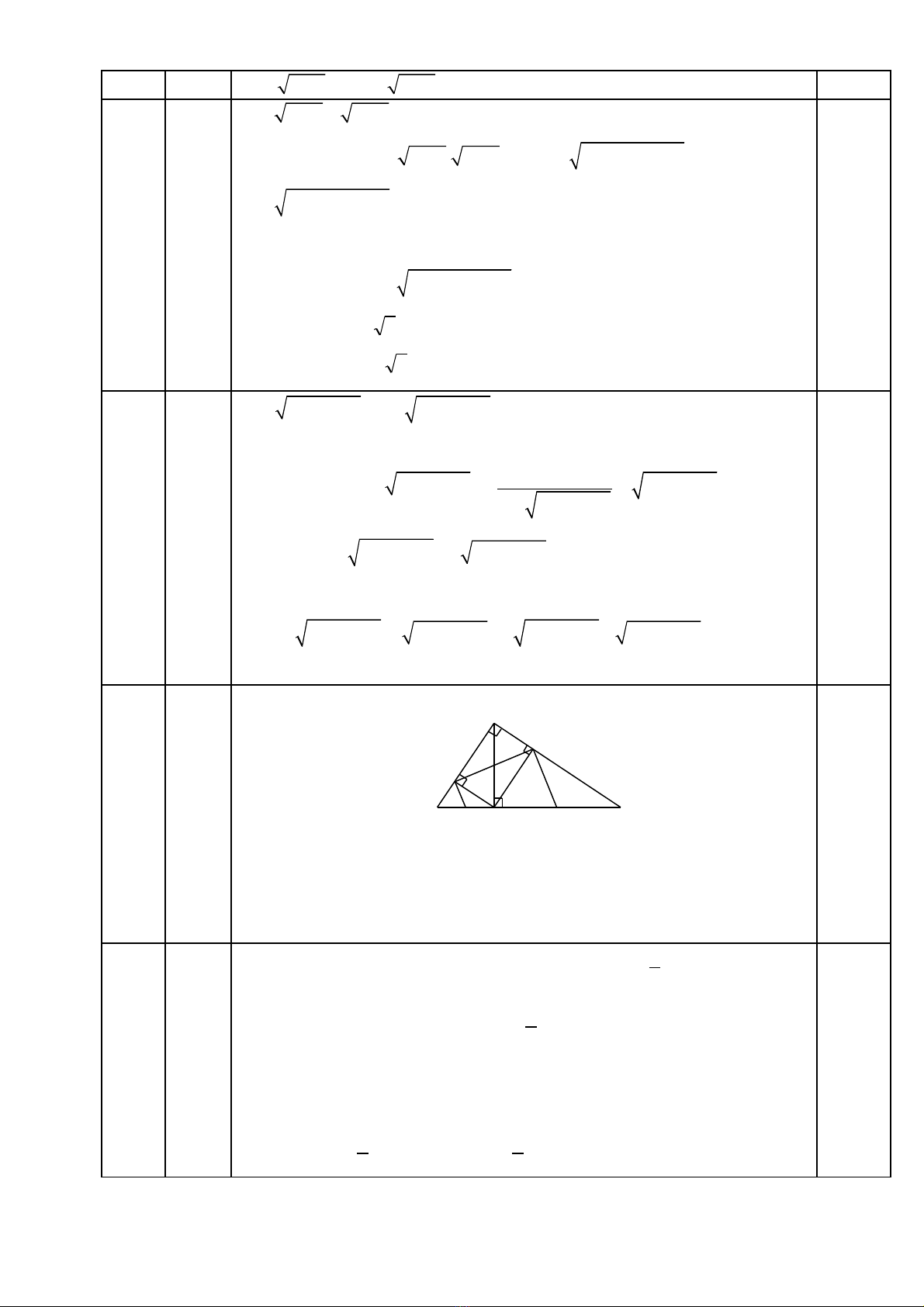
Câu 4. (2,5 đi mể): Cho tam giác ABC vuông t i A, đng cao AH chia c nh huy nạ ườ ạ ề
BC thành hai đo n BH. CH có đ dài l n l t là 4cm, 9cm. G i D và E l n l t là hìnhạ ộ ầ ượ ọ ầ ượ
chi u c a H trên AB và AC. ế ủ
a) Tính đ dài đo n th ng DE.ộ ạ ẳ
b) Các đng th ng vuông góc v i DE t i D và E l n l t c t BC t i M và N. Tínhườ ẳ ớ ạ ầ ượ ắ ạ
di n tích t giác DENM.ệ ứ
Câu 5. (1,5 đi mể) Cho tam giác ABC vuông t i A ( ABạ
<
AC); trung tuy n AM.ế
G i ọ
;
ﾷ
AMB
β
=
. Ch ng minh r ng ứ ằ
( )
2
sin + cos 1 sin .
α α β
= +
------------- Heát -------------
Kú thi chän häc sinh giái líp 9 – N¨m häc 2011 - 2012
Híng dÉn chÊm M«n TO¸N
(Thêi gian lµm bµi 150 phót, kh«ng kÓ thêi gian giao ®Ò)
CâuÝN i dungộđi mể
1 a
1đ
1 x 1 x 1
P x :
x x x x
� �
− −
� �
= − −
� �
� �� �
+
� �� �
, ĐKXĐ:
x 0, x 1>
=
( )
x 1 x 1 x 1
:
x x x 1x
� �
− − −
� �� �
−
� �� �
� � +
� �
=
( )
x 1 x 1 x 1
:
xx x 1
− − − +
+
=
x 1
x
−
:
( )
x x
x x 1
−
+
=
x 1
x
−
( )
( )
x 1
x x 1
x+
−
=
b
0,75đ
V i x = ớ
32
2
ĐKXĐ, x = 4
−
2
3
=
( )
2
3 1−
x 3 1= −
Nên P =
( )
2
3 1 1
3 1
− +
−
=
13
3
=
.
c)
0,75đ
ĐK: x
4
P.
x
= 6
x
−
3
−
4x
.
x
= 6
x
−
3
−
4x
( )
2
x 1+
= 6
x
−
3
−
4x
x + 2
x
+ 1 = 6
x
−
3
−
4x
( )
2
x 2 x 4 0− + − =
(*)
Do
( )
2
x 2 0−
x > 0;
x 4 0−
,
x
4
Nên đ (*) x y ra thì ể ả
( )
2
x 2 0− =
và
x 4 0− =
x = 4 (TM ĐKXĐ)
2 a)
1,0 Ta có
2 2 2
2
1 1 1 1 1 1 2 2 2
a b c a b c ab bc ac
� �
+ + = + + + + +
� �
� �
=
( )
2 2 2
2 a b c
1 1 1
a b c abc
+ +
+ + +
=
2 2 2
1 1 1 0
a b c
+ + +
=
2 2 2
1 1 1
a b c
+ +
2 2 2
2
1 1 1 1 1 1 1 1 1
a b c a b c a b c
� �
+ + = + + = + +
� �
� �
b
1,0
x 7 x 5 2+ − − =
( ĐKXĐ: x
5)
x 7 x 5 2+ = − +
(*)
x + 7 = x – 5 + 4 + 4
x 5−
(do caùc veá (*) khoâng aâm)
N
M
E
D
H
C
B
A
4
x 5−
= 8
x 5−
= 2
x = 9 (
ĐKXĐ)
3 a
0,75
A x 2 6 x= − + −
ĐKXĐ
2 x 6
A 0>�
A2 = x
−
2 + 6
−
x + 2
x 2. 6 x− −
= 4 +
( ) ( )
2 x 2 6 x− −
Vì
( ) ( )
2 x 2 6 x 0− −
Nên A2
4
hay A
2
- Do đó MinA = 2
x = 2 ho c x = 6 ( tm ĐK)ặ
M t khác Aặ2 = 4 +
( ) ( )
2 x 2 6 x− −
4
+ x
−
2 + 6 – x = 8 (theo Cauchy)
A2
8
hay A
22
- Do đó MaxA =
22
x
−
2 = 6
−
x hay x = 4 (tm ĐK)
0,25
0,25
0,25
b
0,75
()()
2 2
x x 2011 y y 2011 2011+ + + + =
(hai nhaân töû v.traùi phaûi
khaùc 0) Nên
()
2 2
2
2011
x x 2011 y 2011 y
y y 2011
+ + = = + −
+ +
T ng tươ ự
2
y y 2011+ +
=
2
x 2011 x+ −
C ng v theo v , ta cóộ ế ế
x + y +
2
y 2011+
+
2
x 2011+
=
2
y 2011+
+
2
x 2011+
−
x
−
y
2(x + y) = 0 nên x + y = 0
4 a)
1,0 Ta có T giác ADHE là hình ch nh t vì có 3 góc vuông nên AH = DEứ ữ ậ
Mà AH2 = BH.CH ( Theo h th c gi a đng cao và hình chi u)ệ ứ ữ ườ ế
Nên AH2 = 4.9 = 36. Do đó AH = 6 cm nên DE = 6 cm.
b)
1,5
C. minh đc: * M là trung đi m c a BH nên DM = ượ ể ủ
2
1
BH = 2 cm
* N là trung đi m c a HC nên EN = ể ủ
2
1
HC = 4,5 cm
Nên t giác DENM là hình thang vuông có 2 đáy 2 cm và 4,5 cm và đngứ ườ
cao DE = 6 cm.
Do đó SDENM =
2
1
(DM + EN).DE =
2
1
(2 + 4,5).6 = 19,5(cm2)
H
M
C
B
A
5
1,5
T A v AH ừ ẽ
BC
Vì AB < AC nên HB < HC.
Do đó H n m gi a B và Mằ ữ
Nên sin
=
AH
AM
=
2AH
BC
( Vì AM =
2
1
BC Theo t/c trung tuy n trong tam giác vuông)ế
M t khác ặ
( )
2
sin cos
α α
+
= sin2
+ cos2
+ 2sin
.cos
= 1 + 2sin
.cos
Mà 2. sin
cos
=
AB AC
2BC BC
� �
=
2
AH.BC 2AH
2BC
BC =�
Do đó sin
= 2.sin
cos
Vì v y ậ
( )
2
sin cos
α α
+
= 1 + sin
.