Đề cương học kì 1 Đại số và Giải tích 12: Từ cơ bản đến nâng cao [mới nhất]

ĐỀ CƯƠNG HỌC KÌ 1 NĂM 2020

2020

Từ cơ bản tới nâng cao

Các dạng toán đa dạng và đầy đủ

dành cho học sinh muốn đạt 8+

Muïc luïc

CHƯƠNG 1. ÖÙNG DUÏNG ÑAÏO HAØM ÑEÅ KHAÛO SAÙT & VEÕ ÑOÀ THÒ HAØM SOÁ

................................................ 1

§ 1. TÍ NH ÑÔN ÑI EÄU CUÛA HAØM SOÁ ......................................................................................................................................... 1

 Daïng toaùn 1: Tìm caùc khoaûng ñôn ñieäu ( khaûo saùt chieàu bieán thieân) ..................................................................................... 2

 Daïng toaùn 2. Tìm tham soá m ñeå haøm soá ñôn ñieäu tr eân mieàn xaùc ñònh cuûa noù .................................................................. 14

 Daïng toaùn 3. M oät soá baøi toaùn vaän duïng & vaän duïng cao thöôøng gaëp ............................................................................... 21

§ 2. CÖÏC TRÒ CUÛA HAØM SOÁ ......................................................................................................................................................... 27

 Daïng toaùn 1: Tìm ñieåm cöïc ñaïi, cöïc tieåu, giaù trò cöïc ñaïi, giaù trò cöïc tieåu ....................................................... 28

 Daïng toaùn 2. Tìm tham soá m ñeå haøm soá ñaït cöïc tr ò taïi ñieåm x = xo cho tröôùc ................................................................ 34

 Daïng toaùn 3. Bieän luaän hoaønh ñoä cöïc tr ò hoaëc tung ñoä cöïc trò

............................................................................................ 37

 Daïng toaùn 4. Moät soá baøi toaùn vaän duïng & vaän duïng cao thöôøng gaëp ................................................................................ 47

§ 3. GI AÙ TRÒ LÔÙN NHAÁT VAØ GI AÙ TRÒ NHOÛ NHAÁT CUÛA HAØM SOÁ

............................................................................... 57

 Daïng toaùn 1: Tìm gtnn vaø gtln cuûa haøm soá khi ñeà cho ñoà thò hoaëc baûng bieán thieân ............................................. 58

 Daïng toaùn 2. Tìm giaù tr ò lôùn nhaát vaø giaù tr ò nhoû nhaát cuûa haøm soá tr eân ñoaïn ................................................... 60

 Daïng toaùn 3. Tìm giaù tr ò l ôùn nhaát, giaù trò nhoû nhaát cuûa haøm soá treân khoaûng ................................................... 64

 Daïng toaùn 4. Moät soá baøi toaùn vaän duïng & vaän duïng cao thöôøng gaëp ............................................................. 67

§ 4. ÑÖÔØNG TI EÄM CAÄN ............................................................................................................................... 73

 Daïng toaùn 1: Tìm ñöôøng tieäm caän ñöùng, tieäm caän ngang cuûa ñoà thò haøm soá

...................................................... 74

 Daïng toaùn 2. Baøi toaùn tieäm caän l ieân quan ñeán tham soá ............................................................................... 77

§ 5. KHAÛO SAÙT SÖÏ BI EÁN THI EÂN VAØ VEÕ ÑOÀ THÒ HAØM SOÁ ...................................................................... 85

 Daïng toaùn 1: Nhaän daïng ñoà thò haøm soá

...................................................................................................... 85

 Daïng toaùn 2. Bieán ñoåi ñoà thò

................................................................................................................... 99

 Daïng toaùn 3. Töông giao khi ñeà cho baûng bieán thieân hoaëc ñoà thò

..................................................................... 103

 Daïng toaùn 4. Töông giao cuûa hai haøm cuï theå

.............................................................................................. 114

CHƯƠNG 2. HAØM SOÁ LUYÕ THÖØA, HAØM SOÁ M UÕ, HAØM SOÁ LOGARI T ................................................ 119

§ 1. Coâng thöùc muõ & l ogarit ........................................................................................................................... 119

 Daïng toaùn 1: Coâng thöùc muõ vaø caùc bieán ñoåi ............................................................................................... 119

 Daïng toaùn 2. Coâng thöùc loâgarit vaø caùc bieán ñoåi .......................................................................................... 122

§ 2. Haøm soá luyõ thöøa – Haøm soá muõ – Haøm soá logarit ......................................................................................135

 Daïng toaùn 1: Tìm taäp xaùc ñònh cuûa haøm l uõy thöøa, muõ, l oâgarit ....................................................................... 136

 Daïng toaùn 2. Tìm ñaïo haøm cuûa haøm muõ – l oâgarit ...................................................................................... 140

 Daïng toaùn 3. Ñôn ñieäu vaø cöïc trò cuûa haøm soá muõ & l oâgarit .......................................................................... 143

 Daïng toaùn 4. Giaù trò l ôùn nhaát vaø giaù trò nhoû nhaát cuûa haøm soá muõ & loâgarit .................................................... 146

 Daïng toaùn 5. Nhaän daïng ñoà thò haøm soá muõ – l uõy thöøa vaø l oâgarit ................................................................ 149

 Daïng toaùn 5. Baøi toaùn laõi suaát vaø moät soá baøi toaùn thöïc teá khaùc .................................................................... 153

§ 3. Phöông trình muõ, phöông tr ình l ogarit .................................................................................................... 165

 Daïng toaùn 1: Phöông trình muõ & l oâgarit cô baûn ( hay ñöa veà cuøng cô soá) ........................................................ 165

 Daïng toaùn 2. Giaûi phöông trình muõ – l oâgarit baèng caùch ñaët aån phuï

............................................................. 173

 Daïng toaùn 3. Baøi toaùn chöùa tham soá trong phöông trình muõ & l oâgarit ( naâng cao) ........................................... 178

 Daïng toaùn 4. Phöông phaùp haøm soá ( naâng cao) ........................................................................................... 185

§ 4. Baát phöông trình muõ – Baát phöông trình l ogarit .................................................................................... 189

 Daïng toaùn 1: Baát phöông tr ình muõ & loâgarit cô baûn hoaëc ñöa veà cuøng cô soá

.................................................... 189

 Daïng toaùn 2. Phöông phaùp ñaët aån phuï hoaëc phöông phaùp ñaùnh giaù

................................................................ 193

 Daïng toaùn 3. Tìm m ñeå baát phöông trình nghieäm ñuùng, coù nghieäm ( naâng cao) .................................................. 197

ĐỊA CHỈ GHI DANH:



TRUNG TÂM THẾ VINH – 45A LÊ THÚC HOẠCH – Q. TÂN PHÚ (ĐỐI DIỆN TRƯỜNG THPT TRẦN PHÚ).



TRUNG TÂM HOÀNG GIA – 56 PHỐ CHỢ – P. TÂN THÀNH – Q. TÂN PHÚ (SAU CHỢ TÂN PHÚ).



71/25/10 PHÚ THỌ HÒA – P. PHÚ THỌ HÒA – Q. TÂN PHÚ – TP. HỒ CHÍ MINH.

ĐIỆN THOẠI GHI DANH:



0983.047.188 – Zalo (Thầy Nguyễn Đức Nam) – Face: https://www.facebook.com/marion.zack/



0933.755.607 – Zalo (Thầy Lê Văn Đoàn) – 0929.031.789 – Face: https://www.facebook.com/levan.doan.902

NHÓM TOÁN THẦY LÊ VĂN ĐOÀN:

Ths. Lê Văn Đoàn – Ths. Trương Huy Hoàng – Ths. Nguyễn Tiến Hà – Thầy Bùi Sỹ Khanh – Thầy Nguyễn Đức

Nam – Thầy Đỗ Minh Tiến – Thầy Nguyễn Duy Tùng – Thầy Trần Nguyễn Vĩnh Nghi – Thầy Hoàng Minh

Thiện – Thầy Trần Quốc Tuấn.

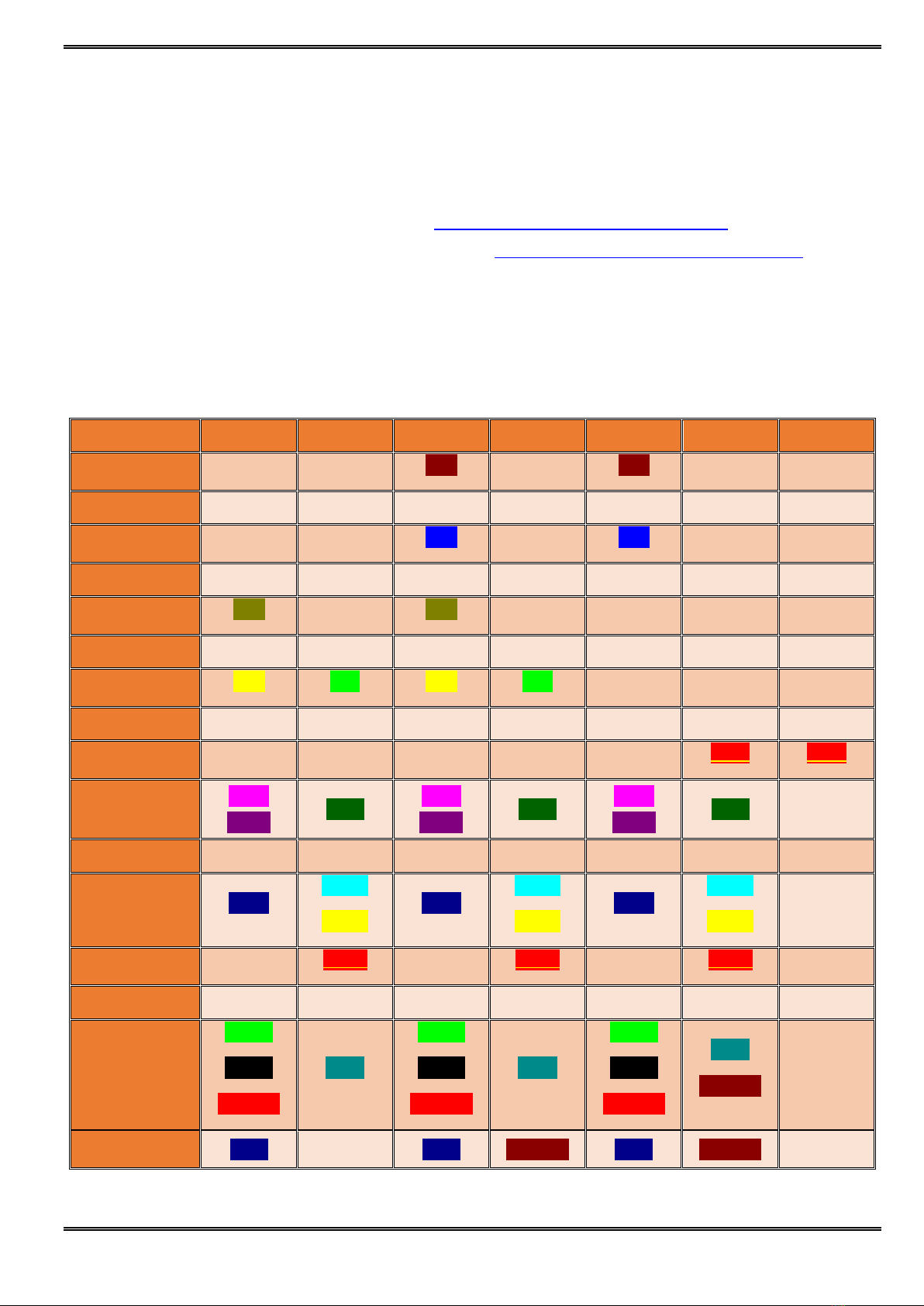
THỜI KHÓA BIỂU CÁC LỚP TOÁN ĐANG HỌC (Sau 05/09 sẽ mở thêm lớp mới, hs theo dõi thông báo):

KHỐI 6 Thứ hai Thứ ba Thứ tư Thứ năm Thứ sáu Thứ bảy Chủ nhật

19’15 – 21’15 T6A T6A

KHỐI 7 Thứ hai Thứ ba Thứ tư Thứ năm Thứ sáu Thứ bảy Chủ nhật

17’30 -19’30 T7A T7A

KHỐI 8 Thứ hai Thứ ba Thứ tư Thứ năm Thứ sáu Thứ bảy Chủ nhật

19’15 – 21’15 T8A T8A

KHỐI 9 Thứ hai Thứ ba Thứ tư Thứ năm Thứ sáu Thứ bảy Chủ nhật

17’30 -19’30 T9A T9B T9A T9B

KHỐI 10 Thứ hai Thứ ba Thứ tư Thứ năm Thứ sáu Thứ bảy Chủ nhật

17’45 -19’15 T10C T10C

19’30 – 21’00 T10A

10HG T10B T10A

10HG T10B Giải đề

KHỐI 11 Thứ hai Thứ ba Thứ tư Thứ năm Thứ sáu Thứ bảy Chủ nhật

17’45 -19’15 T11A T11B1

T11B2 T11A T11B1

T11B2 Giải đề

19’30 – 21’00 T11-C T11-C T11-C

KHỐI 12 Thứ hai Thứ ba Thứ tư Thứ năm Thứ sáu Thứ bảy Chủ nhật

17’45 -19’15

T12A1

T12A2

T12HG1

T12C

T12A1

T12A2

T12HG1

T12C

T12A1

T12A2

T12HG1

T12C

T12HG2

Lớp

chuyên đề

VD và

VDC

19’30 – 21’00 T12B T12B T12HG2 T12B T12HG2

§iÖn tho¹i ghi danh: 0983.047.188 (ThÇy Nam) – 0933.755.607 (ThÇy §oµn) Chuyªn ®Ò: Hµm sè

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 1 -

Chöông 1. ÖÙNG DUÏNG ÑAÏO HAØM ÑEÅ KHAÛO SAÙT & VEÕ ÑOÀ THÒ HAØM SOÁ

§ 1. TÍ NH ÑÔN ÑI EÄU CUÛA HAØM SOÁ

A. KIẾN THỨC CƠ BẢN

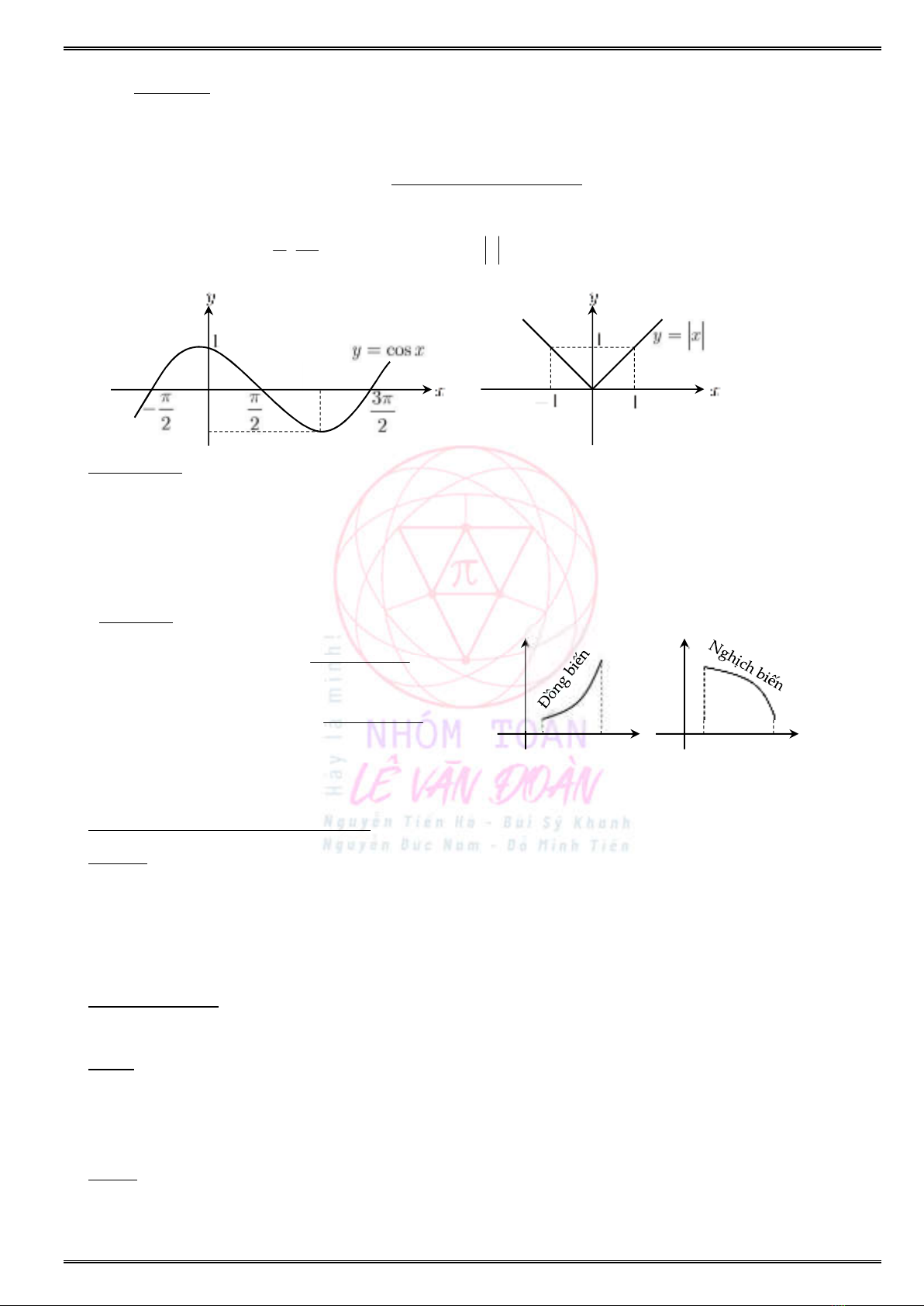
Từ đồ thị hình

và hình

bên dưới, hãy chỉ các khoảng tăng (đồng biến), giảm (nghịch biến) của hàm

số

cosy x

trên đoạn 3

;

2 2

 

 

 



 

 

và của hàm số

y x

trên khoảng ( ; )  ?

1. Định nghĩa

Cho hàm số ( )y f x xác định trên

với

là khoảng hoặc đoạn hoặc nửa khoảng.

— Hàm số ( )y f x đồng biến (tăng) trên

nếu 1 2 1 2 1 2

, , ( ) ( ).x x K x x f x f x    

— Hàm số ( )y f x nghịch biến (giảm) trên

nếu 1 2 1 2 1 2

, , ( ) ( ).x x K x x f x f x    

Hàm số đồng biến hoặc nghịch biến trên

được gọi chung là đơn điệu trên

Nhận xét: Từ định nghĩa, nếu 1 2

, x x K  và 1 2

x x thì hàm số:

— ( )f x đồng biến trên 2 1

2 1

( ) ( ) 0.

f x f x

Kx x



 



( )f x nghịch biến trên 2 1

2 1

( ) ( ) 0.

f x f x

Kx x



 



— Nếu hàm số đồng biến trên

thì đồ thị đi lên từ trái sang phải và nghịch biến trên

thì đồ thị đi

xuống từ trái sang phải.

2. Tính đơn điệu và dấu của đạo hàm

Định lí (thừa nhận): Giả sử hàm số ( )y f x có đạo hàm trên khoảng

— Nếu ( ) 0, f x x K

   thì hàm số đồng biến trên khoảng

— Nếu ( ) 0, f x x K

   thì hàm số nghịch biến trên khoảng

Nếu ( ) 0, f x x K

   thì hàm số không đổi trên khoảng

Định lí mở rộng: Nếu ( ) 0, f x x K

   (hoặc ( ) 0, )f x x K

   và ( ) 0f x

 chỉ tại một số điểm

hữu hạn của

thì hàm số đồng biến (nghịch biến) trên khoảng

Ví dụ: Hàm số 3 2

2 6 6 7y x x x   

xác định trên



Ta có: 2 2

6 12 6 6( 1) .y x x x

    

Do đó 0 1y x

    và 0, 1.y x

  

Theo định lí mở rộng, hàm số luôn đồng biến trên ( ; ). 

Lưu ý: Nếu

là một đoạn hoặc nửa khoảng thì phải bổ sung giả thiết “hàm số ( )y f x liên tục

trên đoạn hoặc nửa khoảng đó”. Chẳng hạn: Nếu hàm số ( )y f x liên tục trên [ ; ]a b và có đạo hàm

( ) 0, f x x K

   trên khoảng ( ; )a b thì hàm số đồng biến trên đoạn [ ; ].a b

(Hình 2)

(Hình 1)

§iÖn tho¹i ghi danh: 0983.047.188 (ThÇy Nam) – 0933.755.607 (ThÇy §oµn) Chuyªn ®Ò: Hµm sè

Ths. Lª V¨n §oµn - Ths. Tr¬ng Huy Hoµng - Ths. NguyÔn TiÕn Hµ - Bïi Sü Khanh - NguyÔn §øc Nam - §ç Minh TiÕn Trang - 2 -

Daïng toaùn 1: Tìm caùc khoaûng ñôn ñieäu (khaûo saùt chieàu bieán thieân)



 Bài toán. Tìm các khoảng đơn điệu (khảo sát chiều biến thiên) của hàm số ( ).y f x

 Phương pháp:

 Bước 1. Tìm tập xác định

của hàm số. Tính đạo hàm ( ).y f x

 



 Bước 2. Tìm các điểm tại đó ( ) 0f x

 hoặc ( )f x

 không xác định.

 Bước 3. Sắp xếp các điểm theo thứ tự tăng dần và lập bảng biến thiên (xét dấu ).y



Bước 4. Từ bảng biến thiên, kết luận:



 

đồng biến và



 

nghịch biến.

1. Hàm số 3 2

3 1y x x  

đồng biến trên

khoảng nào dưới đây ?

A. (0;2). B. (1; ).

C. ( ;0). D. ( ;1).

2. Hàm số 3 2

3 9y x x x   

nghịch biến trên

khoảng nào dưới đây ?

A. ( 1; 3). B. (3; ).

C. (2;4). D. ( ;1).

Lời giải. Tập xác định

.D

3 6 , 0 0 2.y x x y x x

 

      

Bảng biến thiên (xét dấu ) :y





y



0  0



Chọn đáp án C.

........................................................................................

3. Hàm số 3

3 12y x x  

nghịch biến trên

khoảng nào sau đây ?

A. (0;2). B. (1; ).

C. ( ; 1).  D. ( 1;1).

4. Hàm số 3 2

( ) 3 9 11f x x x x    

đồng biến

trên khoảng nào sau đây ?

A. (3; ). B. ( 1; ). 

C. ( 1; 3). D. ( ;3).

..................................................................................

........................................................................................

5. Hàm số nào sau đây luôn đồng biến trên

.

A. 3

3 .y x x 

B. 3

2 .y x x  

C. 4 2

2 .y x x 

D. 3 2

4 .

y x x x  

6. Hàm số nào sau luôn nghịch biến trên

.

A. 3

4 .y x x  

B. 3 2

3 3 .y x x x   

C. 4 2

2 .y x x 

D. 3 2

4 .y x x x  

..................................................................................

........................................................................................

Đề cương học kì 1 Đại số và Giải tích 12 – Từ cơ bản đến nâng cao

Tài liêu mới

Tài liệu Tổng hợp bài tập định lý Viète

Bài tập ôn luyện ngữ pháp tiếng Anh cơ bản

Bài tập vận dụng về từ vựng, ngữ pháp tiếng Anh

Bài tập So sánh hơn và nhất của tính từ

Tài liệu tham khảo Tiếng Anh lớp 8

Đề ôn tập Vật lí lớp 12

Tài liệu chuyên đề: Cực trị hàm số

Câu hỏi trắc nghiệm ôn tập môn Toán lớp 11

Tài liệu Tổng hợp lý thuyết Toán lớp 8

Tài liệu Lý thuyết và bài tập Tiếng Anh lớp 6

Tài liệu Bài tập cơ bản và nâng cao Đại số 7 (Dành cho giáo viên, phụ huynh)

Tài liệu bồi dưỡng học sinh giỏi môn Lịch sử lớp 9 (Sách Kết nối tri thức)

Tài liệu Hình học 9 - Chương 5: Đường tròn - Tự luận có lời giải (Sách Kết nối trí thức với cuộc sống)

Phiếu bài tập cuối tuần Tiếng Việt 1 - Tuần 1 đến tuần 5

Phiếu bài tập cuối tuần Tiếng Việt 1 - Tuần 2 - Đề 4

Giới thiệu

Về chúng tôi

Việc làm

Quảng cáo

Liên hệ

Chính sách

Thoả thuận sử dụng

Chính sách bảo mật

Chính sách hoàn tiền

DMCA

Hỗ trợ

Hướng dẫn sử dụng

Đăng ký tài khoản VIP

093 303 0098

support@tailieu.vn

Phương thức thanh toán

Theo dõi chúng tôi

Facebook

Youtube

TikTok

Đề cương học kì 1 Đại số và Giải tích 12 – Từ cơ bản đến nâng cao

Tài liêu mới

AI tóm tắt

Giới thiệu tài liệu

Đối tượng sử dụng

Từ khoá chính

Nội dung tóm tắt

Hỗ trợ

Phương thức thanh toán

Theo dõi chúng tôi