së gd&®t th¸i b×nh
tr−êng thpt b¾c ®«ng quan
®Ò kiÓm tra chÊt l−îng häc kú II-lÇn II
m«n : To¸n 12 N¨m häc 2008-2009
( Thêi gian lμm bμi 150, kh«ng kÓ giao ®Ò )
I. PhÇn chung dμnh cho tÊt c¶ c¸c thÝ sinh ( 7,0 ®iÓm)
C©u 1 : (3,5 ®iÓm) Cho hμm sè 1
2
x
y
x
−
=
+
1. Kh¶o s¸t vμ vÏ ®å thÞ (C) cña hμm sè
2. ViÕt ph−¬ng tr×nh tiÕp tuyÕn cña (C) biÕt tiÕp tuyÕn ®i qua ®iÓm A(0; -1)
3. Gäi (H) lμ h×nh ph¼ng giíi h¹n bëi (C), trôc hoμnh vμ ®−êng th¼ng y = -3x – 1. TÝnh thÓ
tÝch vËt thÓ trßn xoay sinh bëi (H) khi quay quanh Ox
C©u 2 : (2,0 ®iÓm)
1. Gi¶i bÊt ph−¬ng tr×nh
(
)
1
31
3
log (9 9) log 3 7
xx
x+
+
>− −
2. T×m gi¸ trÞ lín nhÊt, nhá nhÊt cña hμm sè
0
4
() 1 dt
25
x
fx
t
⎛⎞
=−
⎜
−
⎝⎠
∫⎟
trªn ®o¹n [7 ; 16]
C©u 3 : (1,0 ®iÓm) Cho h×nh chãp tam gi¸c ®Òu S.ABC cã diÖn tÝch ®¸y b»ng 3, gãc gi÷a c¹nh bªn
vμ mÆt ®¸y b»ng 450 .X¸c ®Þnh t©m vμ tÝnh diÖn tÝch mÆt cÇu ngo¹i tiÕp h×nh chãp
C©u 4 : (0,5 ®iÓm) Cho c¸c sè thùc d−¬ng x, y. Chøng minh r»ng 2
y
xy
x
y
e
x
++
<
II. PhÇn riªng : (3,0 ®iÓm)
ThÝ sinh häc ch−¬ng tr×nh nμo chØ ®−îc lμm theo ch−¬ng tr×nh ®ã
1. Theo ch−¬ng tr×nh chuÈn
C©u 5a : (2,0 ®iÓm) Trong kh«ng gian Oxyz cho ®−êng th¼ng '
1
2'
:5
3
4
xt
dy t
z
=−
⎧
⎪
−+
⎨
⎪=
⎩
Hai mÆt ph¼ng (α) vμ (α’) lÇn l−ît cã ph−¬ng tr×nh lμ x + y -3 = 0 vμ x + 2z -1 = 0
1. Chøng tá (α) c¾t (α’). ViÕt ph−¬ng tr×nh tham sè cña ®−êng th¼ng d2 lμ giao tuyÕn cña hai
mÆt ph¼ng (α) vμ (α’)
2. Chøng tá d1 vμ d2 chéo nhau. TÝnh kho¶ng c¸ch gi÷a d1 vμ d2
C©u 6a : (1,0 ®iÓm) Trong mÆt ph¼ng phøc cho bèn ®iÓm A, B, C, D lÇn l−ît biÓu diÔn cho bèn sè
phøc 4.
(3 3) ; (3+ 3) ; 1 + 3i ; 2 + (1+ 3)iii++
Chøng minh r»ng bèn ®iÓm A, B, C, D cïng thuéc mét ®−êng trßn
2. Theo ch−¬ng tr×nh n©ng cao
C©u 5b : (2,0 ®iÓm) Trong kh«ng gian Oxyz cho ba ®iÓm 11
( ;0;0), K(0; ;0)
22
Hvμ 1
(1;1; )
3
I .
1. Chøng tá ba ®iÓm H, I, K kh«ng th¼ng hμng. TÝnh diÖn tÝch cña tam gi¸c HIK
2. ViÕt ph−¬ng tr×nh tham sè cña ®−êng th¼ng d lμ h×nh chiÕu vu«ng gãc cña trôc Ox trªn
mÆt ph¼ng (HIK)
C©u 6b : (1,0 ®iÓm) Gi¶i ph−¬ng tr×nh sau trªn tËp c¸c sè phøc :
10 5
2
10
(1 ) ( 3 )
(1 3)
ii
z
i
−+
=−−
---------------------HÕt------------------------
Hä vμ tªn thÝ sinh :...........................................................Sè b¸o danh ......http:laisac.page.tl
së gd&®t th¸i b×nh
tr−êng thpt b¾c ®«ng quan
kiÓm tra chÊt l−îng häc kú II - lÇn II
m«n : To¸n 12  N¨m häc 2008-2009
h−íng dÉn chÊm vμ biÓu ®iÓm
Néi dung §iÓm
C©u 1 : (3,5 ®iÓm) Cho hμm sè 1
2
x
y
x
−
=
+
1. Kh¶o s¸t vμ vÏ ®å thÞ (C) cña hμm sè
2. ViÕt ph−¬ng tr×nh tiÕp tuyÕn cña (C) biÕt tiÕp tuyÕn ®i qua ®iÓm A(0;-1)
3. Gäi (H) lμ h×nh ph¼ng giíi h¹n bëi (C) , trôc hoμnh vμ ®−êng th¼ng
y = -3x – 1 . TÝnh thÓ tÝch vËt thÓ trßn xoay sinh bëi (H) khi quay quanh Ox
a) TËp x¸c ®Þnh : R\{-2} 0,25
b) Sù biÕn thiªn
* Giíi h¹n-tiÖm cËn
,
2
2
, lim
x
x
Lim y y
−
+→−
→− =+∞ =−∞
Do ®ã ®−êng th¼ng x = - 2 lμ tiÖm cËn ®øng cña ®å thÞ hμm sè
, nªn ®−êng th¼ng y = -1 lμ tiÖm cËn ngang cña ®å thÞ hμm sè
1
x
Lim y
→±∞ =−
0,25
1.
(2,0)
* B¶ng biÕn thiªn
+) 2
3
'(2)
yx
−
=+< 0 ,∀x ≠ -2
x -∞ -2 +∞
y’ - -
y -1 +∞
-∞ -1
Hμm sè nghÞch biÕn trªn c¸c kho¶ng (-∞ ;-2) vμ ( -2 ; +∞)
0,25
0,25
0,25
c. §å thÞ
+ Giao víi Oy : (0;1/2)
+ Giao víi Ox : (1;0)
NX : §å thÞ nhËn I(-2;-1) lμ
giao ®iÓm cña hai ®−êng tiÖm
cËn lμm t©m ®èi xøng
0,75
2
(1,0)
+ Gäi x0 lμ hoμnh ®é tiÕp ®iÓm suy ra ph−¬ng tr×nh tiÕp tuyÕn cã d¹ng
()
0
0
2
0
0
1
3() 2
2
x
yxx
x
x
−
−
=−+
+
+
+ V× tiÕp tuyÕn ®i qua A(0;-1) nªn ta cã
()
0
00
2
0
0
1
3
1()
2
2
x
xx
x
x
1
−
−
−
=−+⇔
+
+=−
0,25
0,5
Suy ra ph−¬ng tr×nh tiÕp tuyÕn lμ : y = -3x-1 0,25
3
(0,5)
+) §T y = -3x-1lμ tiÕp tuyÕn t¹i tiÕp ®iÓm (-1;2) vμ c¾t trôc hoμnh t¹i ®iÓm(-1/3;0)
Theo h×nh vÏ ë trªn (TiÕp tuyÕn nμy kh«ng c¾t (C) t¹i mét ®iÓm nμo kh¸c n÷a)
+ Gäi (H1) lμ h×nh ph¼ng giíi h¹n bëi (C) , Ox , x = -1,x=1.Suy ra thÓ tÝch vËt thÓ
trßn xoay sinh bëi (H1) khi quay quanh Ox lμ
22
11 1
12
11 1
13 96
11
22 2
(2)
x
Vdx dx
xx x
x
ππ π
−− −
⎛⎞
−
⎛⎞ ⎛ ⎞
==−=−
⎜⎟
⎜⎟ ⎜ ⎟
++ +
+
⎝⎠ ⎝ ⎠ ⎝⎠
∫∫ ∫ dx+
§Æt x+2=u ⇒ du=dx ; x= -1⇒ u=1 , x=1 ⇒ u =3
3
1
ln
3
12
1
96 9
16(86ln3)Vduuu
uu
u
ππ π
⎛⎞⎛ ⎞
= −+ =−− +=−
⎜⎟⎜ ⎟
⎝⎠⎝ ⎠
∫
0,25
+ Gäi (H2) lμ h×nh ph¼ng giíi h¹n bëi tiÕp tuyÕn (ý 2), Ox, x = -1, x =-1/3 .
Suy ra thÓ tÝch khèi trßn xoay sinh bëi (H2) khi quay quanh Ox b»ng thÓ tÝch cña
khèi nãn trßn xoay cã b¸n kÝnh ®¸y b»ng 2 vμ chiÒu cao b»ng 2/3
⇒ 2
2
12 8
..(.2)
33 9
V
π
π
==
+ ThÓ tÝch khèi trßn xoay cÇn t×m lμ V = V1 – V2 = π64 6ln3
9
⎛⎞
−
⎜⎟
⎝⎠
(§vtt)
0,25
C©u 2 : (2,0 ®iÓm)
1. Gi¶i bÊt ph−¬ng tr×nh
(
)
1
31
3
log (9 9) log 3 7
xx
x+
+
>− −
2. T×m gi¸ trÞ lín nhÊt , nhá nhÊt cña hμm sè
0
4
() 1 dt
25
x
fx
t
⎛⎞
=−
⎜⎟
−
⎝⎠
∫
trªn ®o¹n [7 ; 16]
+ §iÒu kiÖn > 0
1
3
x+−73
7
log 3
x⇔> (*)
0,25
1.
(1,0)
+ §−a bÊt ph−¬ng tr×nh vÒ d¹ng 2.9x -7. 3x – 9 < 0
+ Gi¶i ra 3
9
log 2
x<
0,25
0,25
+ KÕt hîp víi (*) suy ra 3
79
log log
32
x<< 3
( KÕt luËn ) 0,25
+
1
2
00
( ) d 4 (25 ) d(25- )
xx
f
xt t
−
=+ −
∫∫ t
+ TÝnh ®−îc () 8 25 40fx x x=+ −− ( X¸c ®Þnh vμ liªn tôc trªn ®o¹n [7 ; 16] )
0,25
0,25
2.
(1,0) + Ta cã 4
'( ) 1 25
fx
x
=− − vμ '( ) 0 9 (7;16)fx x
=
⇔=∈
0,25
+ f(7) = 24 2 33− ; f(9 ) = 1 ; f(16) = 0
Suy ra
[] []
7;16 7;16
ax ( ) 1 , min ( ) 0mfx fx
=
=
0,25
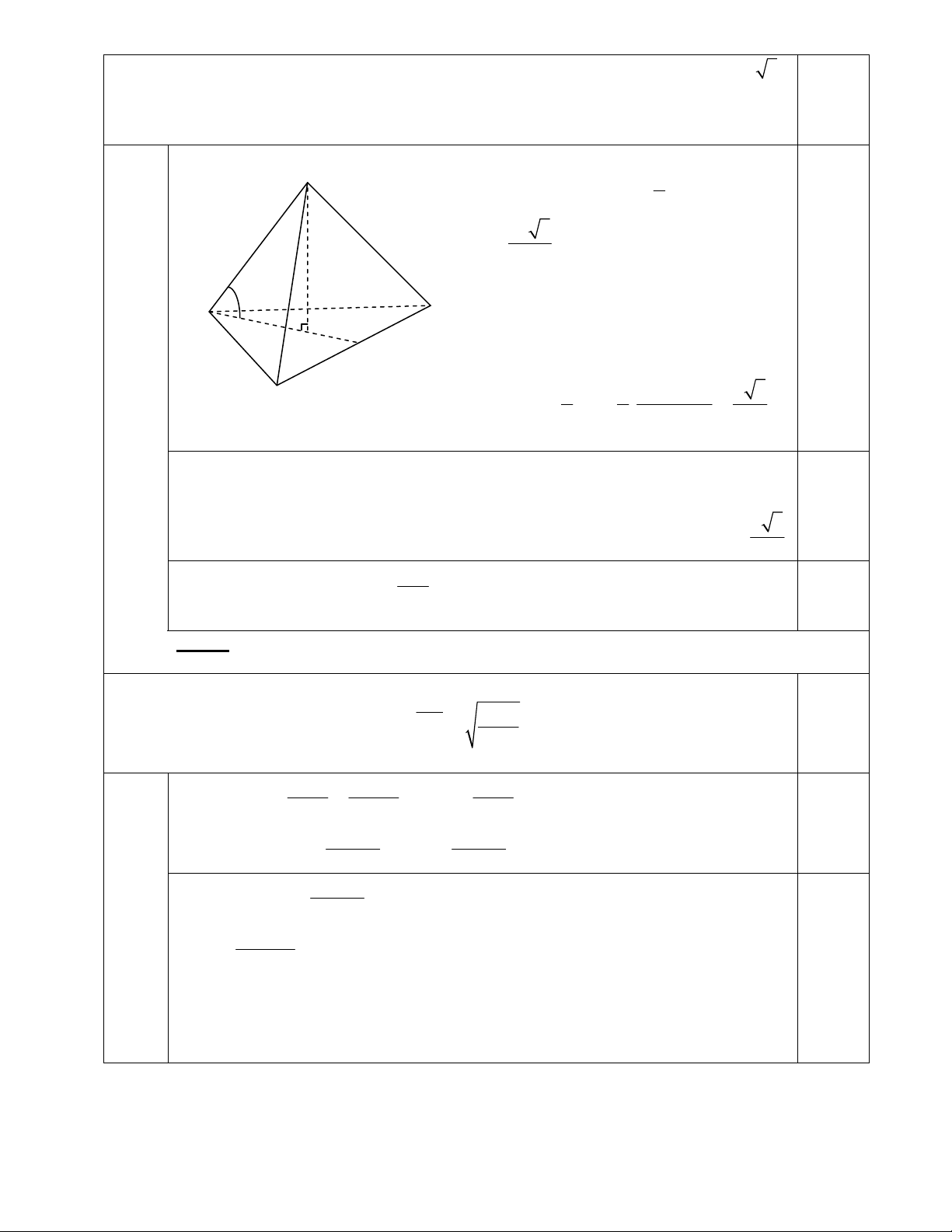
C©u 3 : (1,0 ®iÓm) Cho h×nh chãp tam gi¸c ®Òu S.ABC cã diÖn tÝch ®¸y b»ng 3
gãc gi÷a c¹nh bªn vμ mÆt ®¸y b»ng 450 .X¸c ®Þnh t©m vμ tÝnh diÖn tÝch mÆt cÇu
ngo¹i tiÕp h×nh chãp
+ Gäi tam gi¸c ®Òu ABC cã c¹nh ®¸y
b»ng x ⇒ dtΔABC = 20
1sin 60
2x
23x
=
4
Theo gi¶ thiÕt ⇒ x = 2
+ Gäi H lμ h×nh chiÕu vu«ng gãc cña S
trªn (ABC) ⇒ HA = HB = HC
hay H lμ träng t©m tam gi¸c ABC
⇒ 222 23
.
33 3
dt ABC
AI BC
Δ
== =
HA
(V× AI ⊥ BC)
0,25
0,25
MÆt kh¸c gãc gi÷a c¹nh bªn vμ mÆt ®¸y h×nh chãp = (SA,(ABC))=(SA,AH)
= ∠⇒ ΔSAH vu«ng c©n t¹i H ⇒ HS = HA = HB = HC
0
45SAH
S
A
B
450
H I
C
=
Suy ra H lμ t©m mÆt cÇu ngo¹i tiÕp h×nh chãp S.ABC cã b¸n kÝnh R = HA = 23
3
0,25
DiÖn tÝch mÆt cÇu S= 4πR2 = 16
3
π
0,25
Chó ý : NÕu häc sinh x¸c ®Þnh kh«ng chÝnh x¸c vÞ trÝ t©m cña mÆt cÇu mμ vÉn
®−a ra ®−îc kÕt qu¶ ®óng vÒ diÖn tÝch mÆt cÇu th× ®−îc 0,5 ®iÓm
C©u 4 : (0,5 ®iÓm) Cho c¸c sè thùc d−¬ng x , y . Chøng minh r»ng
2
y
xy
x
y
e
x
+
+
<
+ ) B§T 2
ln 2
x
yy
x
xy
+
⇔ (1) .§Æt
>
+, t > 1
xyt
x
+
=
(1) trë thμnh lnt > 2( 1)
1
t
t
−
+
2( 1)
ln 0
1
t
tt
−
⇔
−>
+
0,25
+ XÐt f(t) = l 2( 1)
n1
t
tt
−
−+ trªn [1;+∞) ,
[
)
2
2
(1)
'( ) 0, 1; (f'(t) = 0 t = 1)
(1)
t
ft t
tt
−
=≥∀∈+∞ ⇔
+
Suy ra f(t) ®ång biÕn trªn [1;+∞) .Do ®ã t >1 ⇔ f(t) > f(1) = 0
Tõ ®ã suy ra ®iÒu ph¶i chøng minh
0,25
C©u 5a : (2,0 ®iÓm) Trong kh«ng gian Oxyz cho ®−êng th¼ng
1
2'
:5
4
xt
dy t
z
=−
⎧
⎪=− +
⎨
⎪=
⎩
3'
Hai mÆt ph¼ng (α) vμ (α’) lÇn l−ît cã ph−¬ng tr×nh lμ x+y-3 = 0 vμ x + 2z -1 = 0
1. Chøng tá (α) c¾t (α’). ViÕt ph−¬ng tr×nh tham sè cña ®−êng th¼ng d2 lμ
giao tuyÕn cña hai mÆt ph¼ng (α) vμ (α’)
2. Chøng tá d1 vμ d2 chéo nhau. TÝnh kho¶ng c¸ch gi÷a d1 vμ d2
+ (α) cã vÐc t¬ ph¸p tuyÕn lμ (1;1; 0)n
→
(α’) cã vÐc t¬ ph¸p tuyÕn lμ '(1; 0; 2)n
→
DÔ thÊy hai vÐc t¬ kh«ng cïng ph−¬ng (Hay ',nknkR
≠
∈
G
JG
), suy ra (α) c¾t (α’)
0,5
1.
+ d2 lμ tËp hîp tÊt c¶ c¸c ®iÓm M(x;y;z) tho¶ m·n hÖ 30
21
xy
xz 0
+
−=
⎧
⎨
+
−=
⎩
Cho y = 0 ⇒ x =3 vμ z = -1 ⇒
(
)
3; 0; 1M
−
∈ d2
+Do d2 vu«nggãc víi vμ ' nªn dn
→
n
→
2 cã vÐc t¬ chØ ph−¬ng 2,'unn
→→→
⎡
⎤
=
=
⎢
⎥
⎣
⎦(2;-2;-1)
Suy ra ph−¬ng tr×nh tham sè cña d2 lμ
32
2
1
x
t
yt
zt
=
+
⎧
⎪=−
⎨
⎪
=
−−
⎩
0,25
0,25
+ ChØ ra 2 vÐc t¬ chØ ph−¬ng , cña d
1
u
→
2
u
→
1 vμ d2 kh«ng cïng ph−¬ng , ®ång thêi
hª ph−¬ng tr×nh sau v« nghiªm suy ra d
32 2'
253
14
tt
t
t
+=−
⎧
⎪−=−+
⎨
⎪−− =
⎩
't1 vμ d2 chéo nhau
0,5
2. + MÆt ph¼ng (β) chøa d2 vμ //d1 , suy ra (β) ®i qua M vμ cã vÐc t¬ ph¸p tuyÕn
n
β
→vu«ng gãc víi (-2; 3;0) vμ nªn lÊy
1
u
→
2
u
→
n
β
→= [ , ]=(-3;-2;-2)
1
u
→
2
u
→
⇒ Ph−¬ng tr×nh (β) : -3(x-3) - 2y - 2(z+1) = 0 ⇔ - 3x - 2y - 2z + 7 = 0
0,25
+ Kho¶ng c¸ch gi÷a d1 vμ d2 b»ng kho¶ng c¸ch gi÷a d1 vμ (β) vμ còng b»ng
kho¶ng c¸ch gi÷a M1(0;-5;4)∈ d1 vμ (β)
⇒d(d1 , d2)= d(M1, (β))= 222
-3.0 2.( 5) 2.4 7
(3) (2) (2)
−
−− +
−+−+− 9
17
= 0,25
KÕt luËn :