SỞ GIÁO DỤC – ðÀO TẠO ðỀ KIỂM TRA HỌC KỲ II LỚP 12THPT
BÌNH DƯƠNG Năm học 2008 - 2009
Môn : Toán
Thời gian làm bài: 150 phút
( Không kể thời gian phát ñề )
I. PHẦN CHUNG CHO TẤT CẢ THÍ SINH (7 điểm)
Câu I (3 điểm)
Cho hàm số y = x3 – 6x2 + 9x,
1/ Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho.
2/ Tính diện tích hình phẳng giới hạn bởi đồ thị (C), trục hoành và hai đường thẳng
x = 1, x = 2.
Câu II (3 điểm)
1/ Tính tích phân I =
1
0
x
2 1
( x ).e .dx
+
∫.
2/ Giải phương trình log
2
(x – 3) + log
2
(x – 1) = 3.
3/ Cho hàm số y = cos2 3x, chứng minh y" + 18.(2y – 1) = 0.
Câu III (1 điểm)
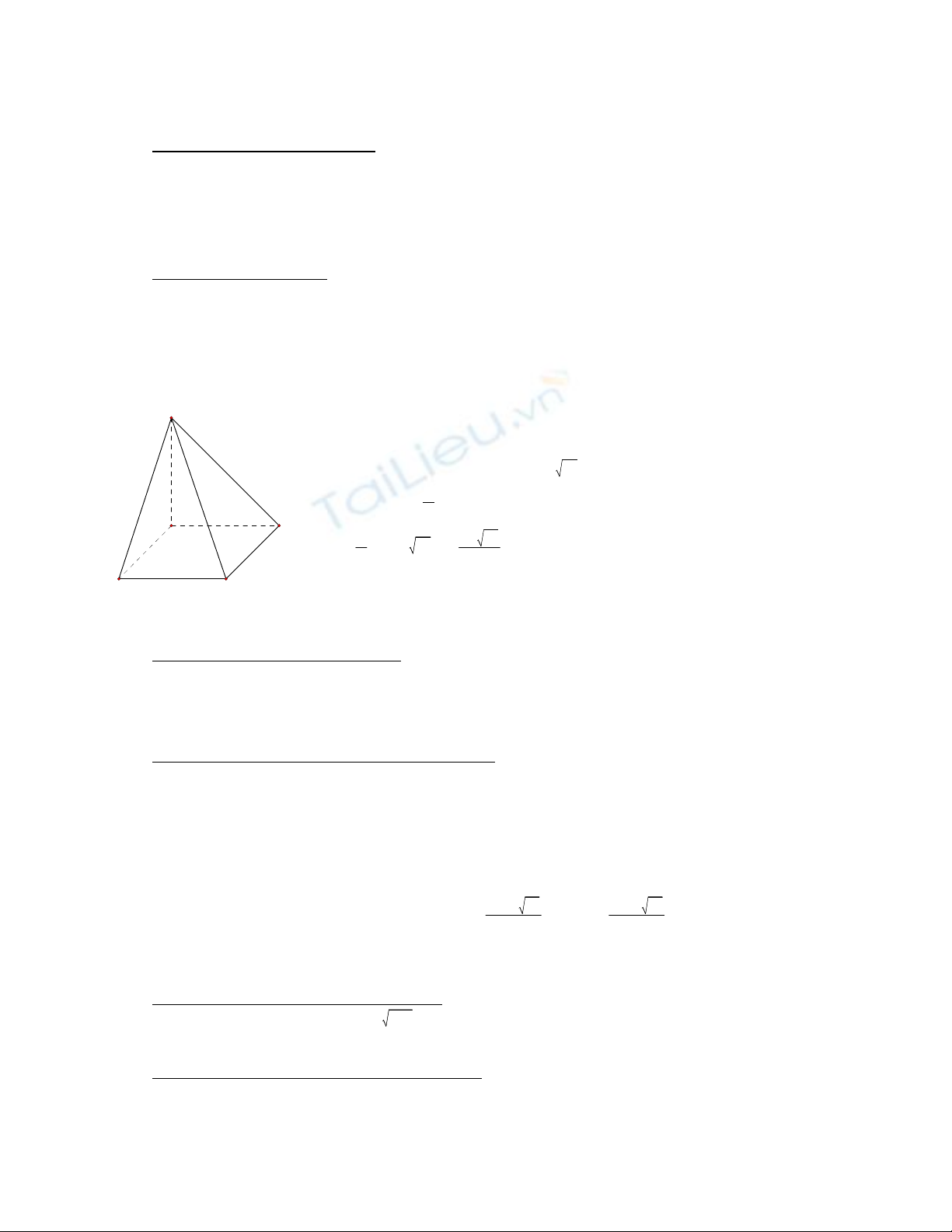
Cho khối chóp S.ABCD có ABCD là hình vuông cạnh a, SB = a
3
và SA vuông góc
mặt phẳng (ABCD). Tính thể tích khối chóp theo a.
II. PHẦN RIÊNG (3 điểm)
Thí sinh học chương trình nào thì chỉ được làm phần dành riêng cho chương trình đó
(phần 1 hoặc 2).
1. Theo chương trình chuẩn:
Câu IV.a (2 điểm)
Trong không gian với hệ toạ độ Oxyz, cho tam giác ABC có A(−1, 1, 2), B(0, 1, 1) và
C(1, 0, 4).
1/ Chứng minh tam giác ABC là tam giác vuông.
2/ Gọi M là điểm thoả
MB
uuur
= 2
MC
uuur
, viết phương trình mặt phẳng (P) qua M và vuông
góc đường thẳng BC.
Câu V.a (1 điểm)
Tìm nghiệm phức của phương trình bậc hai 2z2 – 5z + 4 = 0.
2. Theo chương trình nâng cao:
Câu IV.b (2 điểm)
Trong không gian với hệ toạ độ Oxyz, cho điểm I(3, 4, 2) và mặt phẳng (P) có phương
trình 4x + 2y + z – 1 = 0.
1/ Viết phương trình mặt cầu (S) có tâm I và tiếp xúc mặt phẳng (P).
2/ Cho đường thẳng d có phương trình
1
x
=
2
=
1
3
z
−
, viết phương trình đường thẳng
∆ vuông góc đường thẳng d, qua điểm I và song song với mặt phẳng (P).
Câu V.b (1 điểm)
Cho hàm số y = 2
1
1
x mx
x
− +
−
có
đồ
th
ị
(C), tìm m
để
đồ
th
ị
(C) có 2
đ
i
ể
m c
ự
c
đạ
i và c
ự
c
ti
ể
u tho
ả
y
CĐ
. y
CT
= 5.
------------------
Hết
----------------------
SỞ GIÁO DỤC – ðÀO TẠO KIỂM TRA HỌC KỲ II LỚP 12THPT
BÌNH DƯƠNG Năm học 2008 - 2009
BIỂU ðIỂM – HƯỚNG DẪN CHẤM TOÁN 12
Câu I (3 điểm)
1/
Khảo sát sự biến thiên và vẽ đồ thị (2 điểm)
Mx
đ
: ∀x. 0,25
đ
y' = 3x
2
– 12x + 9 = 0 ↔ x = 1, x = 3. 0,25
đ
x 2
B
ả
ng bi
ế
n thiên: 0,75
đ
x –
∞
1 3 +
∞
y' + 0 – 0 +
y –
∞
C
Đ
(4)
CT(0)
+
∞
(gồm 3 í, mỗi í 0,25đ: dấu y', cực trị, lim y khi x
→
±∞
,
nếu nghiệm của y' hoặc dấu của y' sai thì BBT không cho điểm, kể cả đồ thị).
Đ
i
ể
m ∈
đồ
th
ị
: x = 0 → y = 0 , x = 2 → y = 2.
Đồ
th
ị
: 0,50
đ
2/
Tính diện tích hình phẳng (1 điểm)
d
ự
a vào
đồ
th
ị
, ta có S =
23 2
1
6 9
(x x x).dx
− +
∫
= 0,25
đ
= [
4
4
x
– 2x
3
+
2
9
2
x
]
2
1
=
13
4
. 0,50
đ
+ 0,25
đ
Câu II (3 điểm)
1/
Tính tích phân (1 điểm)
I =
1
0
x
2 1
( x ).e .dx
+
∫
= 2.
1
0
x
x.e .dx
∫
+
1
0
x
e .dx
∫
•
1
0
x
e .dx
∫
= [e
x
]
1
0
= e – 1. 0,25
đ
•
đặ
t u = x → u' = 1, v' = e
x
→ v = e
x
, 0,25
đ
t
ừ
đ
ó
1
0
x
x.e .dx
∫
= [x.e
x
]
1
0
–
1
0
x
e .dx
∫
= 1. 0,25
đ
V
ậ
y I = 2 + e – 1 = 1 + e. 0,25
đ
2/
Giải phương trình (1 điểm)
đ
i
ề
u ki
ệ
n: x > 3. 0,25
đ
khi
đ
ó, pt. ↔ log
2
[(x – 3).(x – 1)] = 3 0,25
đ
↔ x
2
– 4x + 3 = 3 ↔ x
2
– 4x = 0 0,25
đ
↔ x = 4 (lo
ạ
i x = 0) 0,25
đ
3/
Chứng minh (1 điểm)
ta có y' = 2cos3x.(–3sin3x) = –3sin6x 0,25
đ
→ y" = –18cos6x 0,25
đ
t
ừ
đ
ó y" + 18.(2y – 1) = –18cos6x + 18.(2cos
2
3x – 1) =
= –18cos6x + 18cos6x = 0. 0,50
đ
Câu III (1 điểm)
hình v
ẽ
: 0,25
đ
tam giác vuông SAB → SA
2
= SB
2
– AB
2
=
= 3a
2
– a
2
= 2a
2
→ SA = a
2
. 0,25
đ
t
ừ
đ
ó V =
1
3
.S
ABCD
.SA = 0,25
đ
=
1
3
.a
2
.a
2
= 3
2
3
a
. 0,25
đ
1. Theo chương trình chuẩn
:
Câu IV.a (2 điểm)
1/
Tam giác ABC vuông (1 điểm)
ta có:
AB
uuur
= (1, 0, –1),
AC
uuur
= (2, –1, 2) 0,25
đ
x 2
→
AB
uuur
.
AC
uuur
= 0 → AB ⊥ AC 0,25
đ
→ tam giác ABC vuông t
ạ
i A. 0,25
đ
2/
Viết phương trình mặt phẳng (P) (1 điểm)
ta có
MB
uuur
= 2
MC
uuur
→ C là trung
đ
i
ể
m MB → M(2, –1, 7) 0,50
đ
m
ặ
t ph
ẳ
ng (P) qua M và có vpt.
BC
uuur
= (1, –1, 3) 0,25
đ
→ (P): x – 2 – (y + 1) + 3.(z – 7) = 0 ↔ x – y + 3z – 24 = 0. 0,25
đ
Câu V.a (1 điểm)
ta có ∆ = 25 – 32 = –7 = 7i
2
0,25
đ
x 2
t
ừ
đ
ó pt. có 2 nghi
ệ
m ph
ứ
c phân bi
ệ
t là z =
5 7
4
i
+
và z =
5 7
4
i
−
0,25
đ
x 2
2. Theo chương trình nâng cao
:
Câu IV.b (2 điểm)
1/
Viết phương trình mặt cầu (1 điểm)
(S) có bán kính R = d[I, (P)] =
21
0,50
đ
→ ph
ươ
ng trình (S): (x – 3)
2
+ (y – 4)
2
+ (z – 2)
2
= 21 0,50
đ
2/
Viết phương trình đường thẳng (1 điểm)
d có vcp.
a
r
= (1, 2, 3) và (P) có vpt.
n
r
= (4, 2, 1) 0,25
đ
x 2
→ ∆ có vcp. là
a
r
∧
n
r
= (–4, 11, –6) 0,25
đ
→
phương trình
∆
: x = 3 – 4t, y = 4 + 11t, z = 2 – 6t. 0,25đ
Câu V.b (1 điểm)
A
B
DC
S
ta có y' = 2
2
2 1
( 1)
x x m
x
− + −
−, đặt f(x) = x2 – 2x + m – 1 0,25đ
từ đó (C) có 2 điểm cực trị khi f(x) có 2 nghiệm phân biệt
≠
1
↔
∆
' > 0 và f(1)
≠
0
↔
2 – m > 0 và m – 2
≠
0
↔
m < 2 0,25đ
khi đó, 2 điểm cực trị có hoành độ là x1 và x2 nên yCĐ . yCT = 5
↔
(2x1 – m).(2x2 – m) = 5
↔
4x1.x2 – 2m.(x1 + x2) + m2 = 5
↔
4.(m – 1) – 2m.2 + m2 = 5
↔
m2 = 9 0,25đ
↔
m = –3 (loại m = 3) 0,25đ
---------------------------------------------------------------------------------------------------