§¸p ¸n v¾n t¾t vµ biÓu ®iÓm m«n To¸n 12 Ban KHTN - HK2.
Tr−êng THPT ®a phóc
KiÓm tra häc kú 2
N¨m häc: 2008-2009 M«n: To¸n - Líp: 12 Ban KHTN
---------
&
-----------
Thêi gian: 90 phót
Hä tªn häc sinh:…………………………………………………………………………. SBD:
Bµi 1:
(
3.0 ®iÓm
) Cho hµm sè
3
( 1)
y x kx k
= + + +
cã ®å thÞ (C
k
) ( víi k lµ tham sè).
a. Kh¶o s¸t vµ vÏ ®å thÞ (C
-3
) cña hµm sè khi k=-3.
b. TÝnh diÖn tÝch h×nh ph¼ng giíi h¹n bëi (C
-3
) vµ trôc hoµnh.
c. T×m c¸c gi¸ trÞ cña k ®Ó (C
k
) tiÕp xóc víi ®−êng th¼ng (d) cã ph−¬ng tr×nh: y = x + 1.
Bµi 2: (
2.0 ®iÓm
)
a. TÝnh tÝch ph©n sau:
1
1ln
e
I x xdx
x
= +
∫
.
b. Gi¶i ph−¬ng tr×nh sau trªn tËp sè phøc:
2
(3 2 ) 6 0
z i z i
− + + =
.
Bµi 3: (4
.0 ®iÓm
) Trong kh«ng gian víi hÖ täa ®é Oxyz, cho ®iÓm A(2; 5; 3) vµ ®−êng th¼ng (d):
1 2
2 1 2
x y z
− −
= =
vµ ®−êng th¼ng (d'):
3 2 1
.
7 2 3
x y z
− − −
= =
−
a) Chøng minh r»ng (d) vµ (d') chÐo nhau.
b) ViÕt ph−¬ng tr×nh ®−êng vu«ng gãc chung cña (d) vµ (d’)
c) T×m ®iÓm A’ ®èi xøng víi ®iÓm A qua ®−êng th¼ng (d). ViÕt ph−¬ng tr×nh ®−êng th¼ng (d'') ®i qua
A' vµ song song víi (d').
d) ViÕt ph−¬ng tr×nh mÆt ph¼ng (P) chøa ®−êng th¼ng (d) vµ song song víi ®−êng th¼ng (d’).
Bµi 4: (1
.0 ®iÓm
)
Cho a, b, c lµ c¸c sè d−¬ng. Chøng minh r»ng:
( )
3
. . .
a b c
a b c
abc a b c
+ +
≤
HÕt
Tr−êng THPT ®a phóc
KiÓm tra häc kú 2
N¨m häc: 2008-2009 M«n: To¸n - Líp: 12
--------- & ---------- Thêi gian: 90 phót
§¸p ¸n v¾n t¾t vµ biÓu ®iÓm
Chó ý:
Häc sinh lµm ®óng, c¸ch gi¶i kh¸c (lËp luËn ®óng, ®ñ) vÉn cho ®ñ ®iÓm.
Thang
®iÓm
Bµi 1:
(3.0) Cho hµm sè 3
( 1)
y x kx k
= + + +
cã ®å thÞ (C
k
) ( víi k lµ tham sè).
a)
Víi k = -3 hµm sè trë thµnh
3
3 2
y x x
= − −
, TX§: D= R
0.25
(1.0 ®)
- T×m ®−îc ®¹o hµm y', c¸c giíi h¹n, cùc trÞ ...
-
B¶ng biÕn thiªn (®Çy ®ñ th«ng tin)
0.5
-
KÕt luËn vÒ tÝnh
§ång biÕn, nghÞch biÕn, cùc trÞ
0.25
-
Giao ®å thÞ víi c¸c trôc: Oy t¹i (0;
-
2), Ox ...
-
VÏ ®å thÞ hµm sè ...
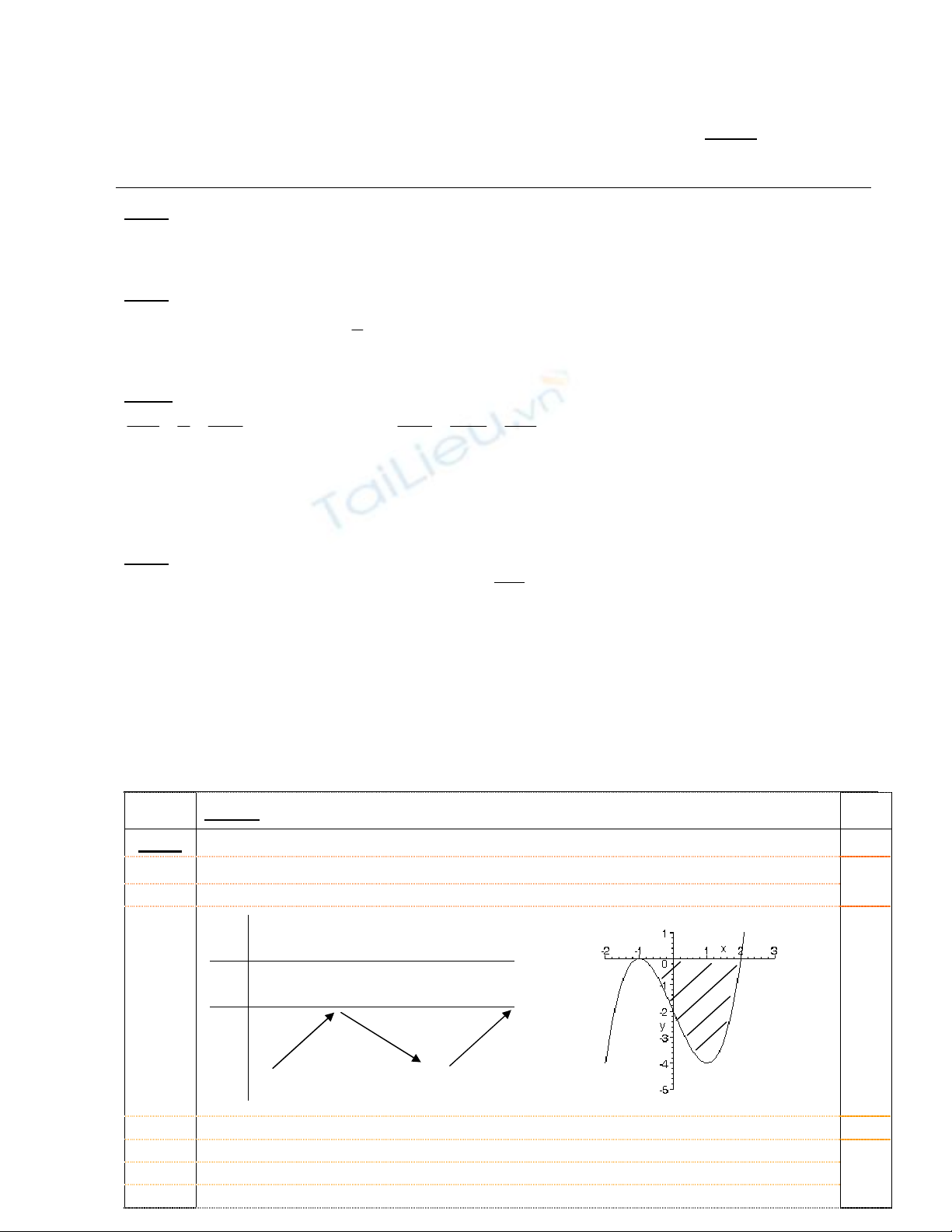
x
-∞ -1 0 1 +∞
y'
+ 0 - 0 +
y
0 -2
-∞ -4
+
∞
§¸p ¸n v¾n t¾t vµ biÓu ®iÓm m«n To¸n 12 Ban KHTN - HK2.
b)
- MiÒn cÇn tÝnh diÖn tÝch lµ miÒn "
g¹ch chÐo
". DiÖn tÝch cÇn tÝnh lµ:
0.25
(1.0 ®)
( )
2
2 2 4
3 3 2
1 1 1
3
3 2 3 2 2 2 4
x
S x x dx x x dx x x
− − −
= − − = − + + = + − =
∫ ∫
27
4
. 0.5
- TÝnh ®−îc ®óng, kÕt luËn. 0.25
c)
(C
k
)
tiÕp xóc víi ®−êng th¼ng (d): y = x + 1 khi vµ chØ khi hÖ sau cã nghiÖm
0.5
(1.0 ®)
3
2
( 1) 1
3 1
x kx k x
x k
+ + + = +
+ =
- Gi¶i hÖ ®óng, kÕt luËn ®óng: k=-2, k=1/4
0.5
Bµi 2:
(2.0 ®iÓm)
a)
(1.0 ®)
TÝnh tÝch ph©n sau:
1 1 1 1
1 ln ln
ln ln ln
e e e e
x x
I x xdx x x dx x xdx dx
x x x
= + = + = +
∫ ∫ ∫ ∫
0.25
TÝnh ®−îc
2
1
1
1
ln
4
e
e
I x xdx
+
= =
∫
(Ph−¬ng ph¸p tõng phÇn)
0.25
TÝnh ®−îc
2
1 1
ln 1
ln (ln )
2
e e
x
I dx xd x
x
= = =
∫ ∫
0.25
KÕt luËn ®óng:
2
1 2
3
4
e
I I I
+
= + =
.
0.25
b)
Gi¶i ph−¬ng tr×nh sau: 2
(3 2 ) 6 0
z i z i
− + + =
.
(1.0 ®)
TÝnh ®−îc:
i125
−
=
∆
0.25
§Ó t×m ®−îc c¨n bËc hai gi¶i ®−îc hÖ ph−¬ng tr×nh
2 2
5
2 12
x y
xy
− =
= −
0.25
Gi¶i ®−îc hÖ, kÕt luËn
∆
cã hai c¨n bËc hai lµ: 3-2i vµ -3+2i. KL pt cã hai ng: z=3; z=2i.
0.5
Bµi 3:
(3.0 ®iÓm)
a.
(1.0 ®)
Cho ®iÓm A(2; 5; 3), (d):
1 2
2 1 2
x y z
− −
= =
vµ (d'):
3 2 1
.
7 2 3
x y z
− − −
= =
−
(d) cã VTCP
(
)
2;1;2
d
u=
uur
qua ®iÓm M(1;0;2);
(d') cã VTCP
(
)
'
7; 2;3
d
u= −
uur
qua ®iÓm M'(3;2;1)
0.25
Ta cã:
( )
'
, 1; 20;11 0
d d
u u
= − − ≠
uur uur r
vµ
'
, . ' 0
d d
u u MM
≠
uur uur uuuuur
0.5
KÕt luËn ®óng (l−u ý cã thÓ lµm c¸ch kh¸c)
0.25
b.
(1.0 ®)
ViÕt ph−¬ng tr×nh ®−êng vu«ng gãc chung cña (d) vµ (d’)
Ph©n
tÝch c¸ch lµm ®óng
1.0
ViÕt ®óng ph−¬ng tr×nh
c.
(1.0 ®)
T×m h×nh chiÕu cña A trªn d. Gäi H lµ h×nh chiÕu vu«ng gãc cña A trªn d.
0.5
Do H
∈
(d)
⇒
H(1+2t;t;2t+2)
⇒
(
)
2 1; 5; 2 1
AH t t t
= − − −
uuur
. Mµ
(
)
. 0 1 3;1; 4 .
d d
AH u AH u t H⊥⇒= ⇔ = ⇒
uuur uur uuur uur
A' ®èi xøng víi A
qua (d). Suy ra ®−îc A'(4;
-
3;3)
(d'') qua A'(4;-3;3) vµ song song víi (d') cã VTCP
(
)
'
7; 2;3
d
u−
uur
, (còng lµ VTCP cña (d''))
0.5
Suy ra (d'') cã ph−¬ng tr×nh:
4 3 3
7 2 3
x y z
− + −
= =
−
.
d. mp(P) chøa (d) vµ song song víi (d')
⇒
(P) qua H(3;1;4) cã VTPT
0.5
§¸p ¸n v¾n t¾t vµ biÓu ®iÓm m«n To¸n 12 Ban KHTN - HK2.
( )
'
, 1; 20;11
P d d
n u u
= = − −
uur uur uur
(1.0 ®)
Suy ra (P): -1(x-3) - 20(y-1) + 11(z-4) = 0
⇔
x + 20y -11z + 20 = 0.
0.5
KÕt luËn ®óng
Bµi 4:
(1.0 ®iÓm)
(1.0 ®)
Cho a, b, c lµ c¸c sè d−¬ng. Chøng minh r»ng:
( )
3
. . .
a b c
a b c
abc a b c
+ +
≤
B§T cÇn CM
ln( ) ln ln ln
3
a b c
abc a a b b c c
+ +
⇔ ≤ + +
0.25
(
)
(
)
(
)
ln ln ln 3 ln ln ln
a b c a b c a a b b c c
⇔ + + + + ≤ + +
0.25
(
)
(
)
(
)
(
)
(
)
(
)
ln ln ln ln ln ln 0
a b a b b c b c c a c a
⇔ − − + − − + − − ≥
Ta cã nhËn xÐt sau:
NÕu 0<
(
)
(
)
ln ln ln ln 0
x y x y x y x y
≤⇒≤⇒− − ≥
0.25
NÕu
(
)
(
)
ln ln ln ln 0
x y x y x y x y
>⇒>⇒− − >
Nh− vËy trong mäi tr−êng hîp ta lu«n cã:
(
)
(
)
ln ln 0
x y x y
− − ≥
suy ra §PCM.
0.25
HÕt