SỞ GD&ĐT THÁI NGUYÊN
TRƯỜNG THPT LƯƠNG PHÚ
ĐỀ KIỂM TRA 45 PHÚT – HỌC KỲ 2
Môn: Đại số và Giải tích lớp 11
(Chương 4)
(Đề tham khảo)
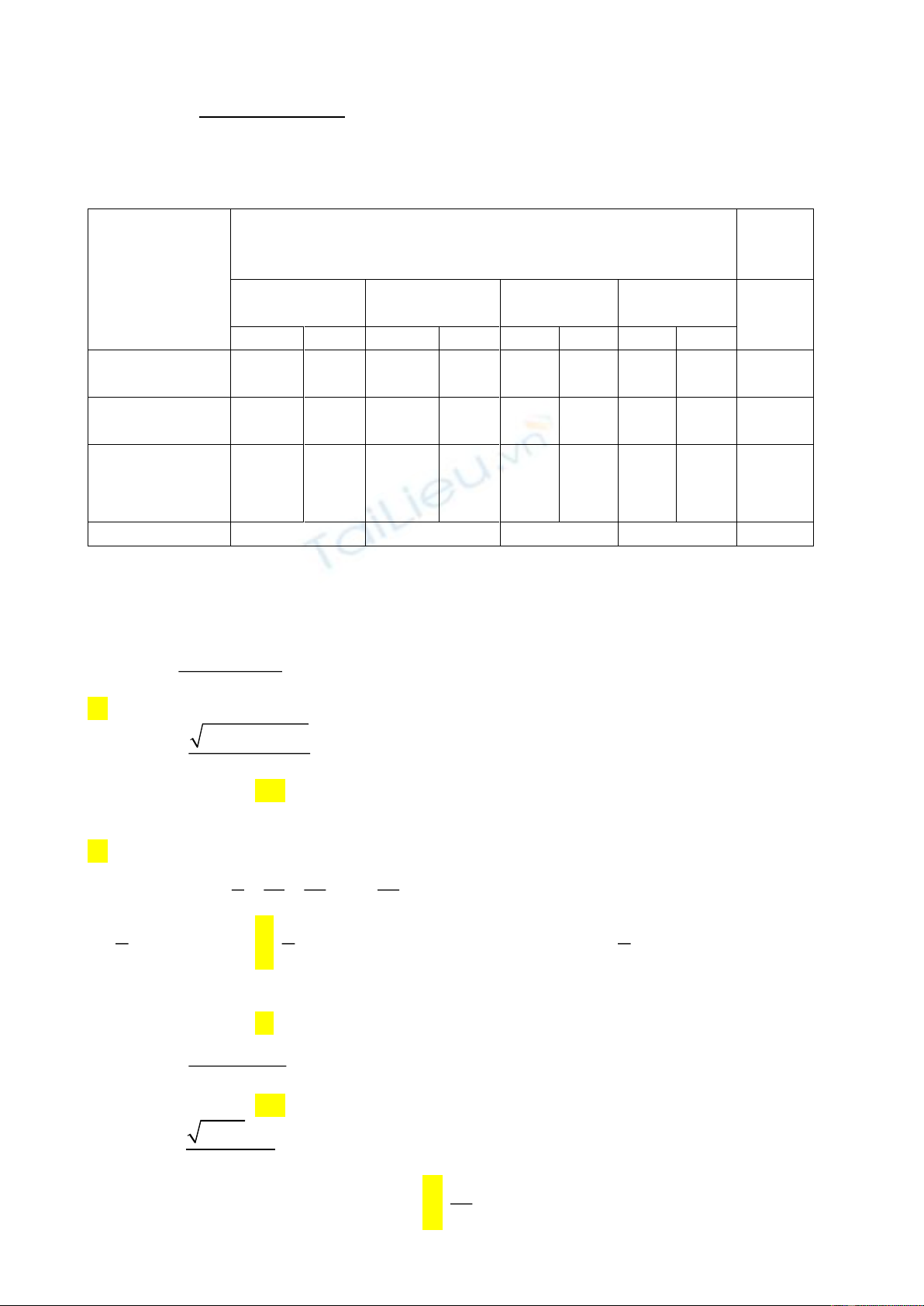
MA TRẬN ĐỀ KIỂM TRA
Các chủ đề
cần đánh giá
Mức độ nhận thức – Hình thức câu hỏi
Tổng
số
điểm
Nhận biêt
Thông hiểu
Vận dụng
cao
TN
TL
TN
TL
TN
TL
TN
TL
Giới hạn dãy
số
1=0,5d
1=0,5d
2=1d
1=1d
3 điểm
Giới hạn hàm
số
2=1d
3=1,5d
1=1d
1=1d
4,5
điểm
Hàm số liên
tục
1=2d
1=0,5d
2,5
điểm
Tổng
3,5
3,5
1,0
10,0
Đề số 1
Phần I. Trắc nghiệm (5 điểm)
Câu 1:
32
43
71
lim
1 5 2
nn
nn


bằng
A.
0
B.
2
C.
1
D.

Câu 2:
2
16 7 3
lim
41
nn
n


bằng
A. 3 B. - 1 C. 1 D. - 4
Câu 3:
3
lim 2 6 11nn
bằng
A.

B. 6 C.

D. 2
Câu 4: Tổng
1 1 1 1
1 ... ...
4 16 64 4n
bằng
A.
5
4
B.
4
3
C. 0 D.
4
5
Câu 5:
3
1
lim 5 4 12
xxx
 
bằng
A. 9 B. 11 C. - 5 D. 3
Câu 6:
2
5
45
lim 5


x
xx
x
bằng
A. - 4 B. - 6 C. 0 D.

Câu 7:
2
4
31
lim
16
x
x
x

bằng
A. 0 B. 2 C.
1
16
D.

Câu 8:
2
2
7 2 18
lim
12 4
x
xx
x


bằng
A.
1
2
B.
1
3
C.
1
2
D.
1
3
Câu 9:
2
lim 4 5
xxx
 
bằng
A.

B. 3 C.

D. 0
Câu 10: Hàm số
223
khi 3
3
3 5 khi 3
xx x
fx x
mx


liên tục tại
3x
khi m bằng
A. 1 B. 4 C. - 2 D. 3
Phần II. Tự luận (5 điểm)
Câu 1: Tính các giới hạn sau:
a)
2
2
2
4
lim 32

x
x
xx
; b)
3
2
3 2 1
lim 2
nn
nn

Câu 2: Cho hàm số
38 khi 2
21 khi x=2
xx
fx x
mx
. Tìm tất cả các giá trị của tham số thực
m
để
hàm số liên tục tại
2x
.
Câu 3. Tính giới hạn
3
1
2 1 3 2
lim 1
x
xx
x
Đáp án
Câu 1.
a)
2
2
2 2 2
22
4 2 2 2
lim lim lim 4
3 2 2 1 1 2 1

x x x
xx
xx
x x x x x
b) Chia cả tử và mẫu cho
3
n
(
3
n
là lũy thừa bậc cao nhất của
n
trong phân thức), ta
được
23
2
21
3
lim lim 21
nnn
u
nn

. Vì
23
21
lim 3 3 0
nn



,
2
21
lim 0
nn




và
2
210
nn

với mọi
n
nên theo quy tắc 3,
lim n
u 
.
Câu 2.
fx
xác định trên .
Ta có
2 2 1fm
và
32
2 2 2
8
lim lim lim 2 4 12
2
x x x
x
f x x x
x
.
(có thể dùng MTCT để tính giới hạn của hàm số)
Để
fx
liên tục tại
2x
thì
2
11
lim 2 2 1 12 2
xf x f m m
.
Câu 3.
Ta có
33
2 1 3 2 2 1 1 1 3 2
1 1 1

x x x x
x x x
2
33
2 2 3 3
2 1 1 1 1 3 2 3 2 1


xx
xx x x x
2
33
23
2 1 1 1 3 2 3 2


xxx
.
Tac có:
12
33
23
lim 0
2 1 1 1 3 2 3 2






xxxx
.
Do đó
3
1
2 1 3 2
lim 0
1
x
xx
x
Đề số 2
Phần I. Trắc nghiệm (5 điểm)
Câu 1. Kết quả đúng của
2
25
lim 3 2.5
n
nn
là:
A.
5
2
. B.
1
50
. C.
5
2
. D.
25
2
.
Câu 2. Kết quả đúng của
2
4
21
lim 32
nn
n
là
A.
3
3
. B.
2
3
. C.
1
2
. D.
1
2
.
Câu 3. Chọn kết quả đúng của
325
lim 35
nn
n

:
A.
5
. B.
2
5
. C.

. D.

.
Câu 4. Giá trị đúng của
22
lim 1 3 2nn
là:
A.

. B.

. C.
0
. D.
1
.
Câu 5.
5
lim 32
xx

bằng:
A.
0
. B.
1
. C.
5
3
. D.

.
Câu 6. Chọn kết quả đúng trong các kết quả sau của
2
3
1
21
lim 22
x
xx
x


là:
A.

. B.
0
. C.
1
2
. D.

.
Câu 7. Chọn kết quả đúng trong các kết quả sau của
32
5
1
21
lim 21
x
xx
x


là:
A.
2
. B.
1
2
. C.
1
2
. D.
2
.
Câu 8. Chọn kết quả đúng trong các kết quả sau của
cos5
lim 2
x
x
x

là:
A.

. B.
0
. C.
1
2
. D.

.
Câu 9. Giá tri đúng của
3
3
lim 3
x
x
x
A. Không tồn tại. B.
0
. C.
1
. D.

.
Câu 10. Cho hàm số
21
1
x
fx x
với
2x
và
2
2 3, 0f m m
. Giá trị của
m
để
fx
liên tục tại
2x
là:
A.
3
. B.
3
. C.
2
. D.
2
Phần II. Tự luận (5 điểm)
Câu 1. Tìm các giới hạn sau
a)

n 2 n 1
n n 1
4.3 2.7
B lim
47
b)

2
3
x2
x 3 2x
lim
x 6 2x 1
Câu 2. Xét tính liên tục của hàm số sau tại
3x
:


2
x3 khi x 3
2x 3 3
fx
x 1 khi x 3
Câu 3. Tính giới hạn
n
x1
x1
A lim x1
.
Đáp án
Câu
1
2
3
4
5
6
7
8
9
10
Đáp
án
D
A
D
B
A
B
A
B
C
C
Câu 1.
a) Ta có:






n
n
42
36 772
B lim 49
47
7
.
b) Ta có:

22
33
x2
x 3 2x 2 3 2.2 7 4
lim 5
x 6 2x 1 2 6 2.2 1
.
Câu 2.
Ta có
f(3) 4
và


2
x 3 x 3
lim f(x) lim (x 1) 4
;

x 3 x 3 x 3 x 3
x 3 2x 3 3
lim f(x) lim lim 3 lim f(x)
2
2x 3 3
Vậy hàm số gián đoạn tại
x3
.
Câu 3.
Ta có:

n n 1 n 2
x 1 (x 1)(x x ... x 1)
Suy ra:

nn 1 n 2
x1
x x ... x 1
x1
Do đó:

n 1 n 2
x1
A lim x x ... x 1 n
.