SỞ GD&ĐT VĨNH PHÚC
—————————
ĐỀ CHÍNH THỨC
KỲ THI CHỌN HSG LỚP 11 THPT NĂM HỌC 2010-2011
ĐỀ THI MÔN: TOÁN
(Dành cho học sinh THPT chuyên Vĩnh Phúc )
Thời gian làm bài: 180 phút, không kể thời gian giao đề.
————————————
Câu I (4 điểm)
1. Giải phương trình:
2
3 1 cos 3 1 sin .cos sin cos 3 0
x x x x x
2. Giải hệ phương trình:
2 2
2 2
2 1
2 3 1 , ,
1
x y
y z x y z
xy yz zx

฀
Câu II (2 điểm)
Giả sử
, , ,
lần lượt là số đo các góc
฀
฀
฀
฀
, , ,
DAB ABC BCD CDA
của tứ giác lồi
ABCD
bất kì.
1. Chứng minh rằng sin sin sin 3sin
3
A B C
A B C
.
2. Tìm giá trị lớn nhất của biểu thức
sin sin sin sin
3
A
P B C D
.
Câu III (1 điểm)
Gọi A là tập hợp các số tự nhiên có tám chữ số đôi một khác nhau. Chọn ngẫu
nhiên một số tự nhiên thuộc vào tập A. Tính xác suất để chọn được một số thuộc A
và số đó chia hết cho
9
.
Câu IV (2,0 điểm)
Cho tam giác ABC. Phân giác trong của các góc A, B, C cắt đường tròn ngoại tiếp tam
giác ABC lần lượt tại các điểm
1 1 1
, ,
A B C
. Đường thẳng
1
AA
cắt đường thẳng
1
CC
tại điểm
I
; đường thẳng
1
AA
cắt đường thẳng
BC
tại điểm
N
; đường thẳng
1
BB
cắt đường thẳng
1 1
A C
tại điểm
P
. Gọi O là tâm đường tròn ngoại tiếp tam giác
1
IPC
. Đường thẳng
OP
cắt
đường thẳng
BC
tại điểm M. Biết rằng
BM MN
và
฀
฀
2
BAC ABC
. Tính các góc của tam
giác ABC.
Câu V (1 điểm)
Cho hàm số
: 0; 0;f
 
thỏa mãn điều kiện
1
3 2 2
2
f x f f x x
với mọi
0
x
. Chứng minh rằng
f x x
với mọi
0
x
.
-------------Hết-------------
Chú ý: Giám thị coi thi không giải thích gì thêm.
Họ và tên thí sinh: ……………………………………………SBD: …………………
SỞ GIÁO DỤC VÀ ĐÀO TẠO
TỈNH VĨNH PHÚC
KÌ THI CHỌN HSG LỚP 11 VÒNG TỈNH
NĂM HỌC 2010 – 2011
HƯỚNG DẪN CHẤM MÔN: TOÁN
(Dành cho học sinh các trường THPT chuyên)
Đáp án gồm 5 trang
Câu Nội dung Điểm
I
4điểm
I.1 (2 điểm)
2
2 2
3 1 cos 3 1 sin .cos sin cos 3 0
3 cos 1 3 sin .cos cos sin .cos sin cos 0
x x x x x
x x x x x x x x
0,5
2 2
3 sin 3 sin .cos cos sin .cos sin cos 0
3 sin sin cos cos sin cos sin cos 0
sin cos 3 sin cos 1 0
x x x x x x x x
x x x x x x x x
x x x x
0,5
2 sin 0
sin cos 0 4
1
3 sin cos 1 sin
6 2
x
x x
x x x
0,5
44
2 2
6 6 2
52
23
6 6
x k x k
x k x k k
x k
x k
฀
0,5
I.2 (2 điểm)
+) Nếu
0
x
thay vào hệ ta có hệ vô nghiệm 0,25
+) Nếu
0
x
ta đặt ;
y ax z bx
thay vào hệ ta được 0,25
2 2
2 2
2 2 2
2 2 2
2
2
2
1 2 1
4 3 1
1 2 2 3
1 2 3 1
2 1 1 0
1 2
1
x a
a b
a a b
x a b a a b a
a a ab b
x a ab b
0,5
2 2 2 2
2
1
1
4 3 1 4 3 1
1 2
1 2 1 1 0 1 2 1 0
2 3 1 0
a
b
a b a b
b a
a a b a a a b
a a
0,5
+) Nếu
1
1
a
b
thay vào (1) không thỏa mãn
0,25
+) Nếu 2
1
1
1 2
1
2 3 1 0
2
0
a
b
b a
a a a
b
thay
1
1
a
b
vào (1) không thỏa mãn, thay
1
2
0
a
b
vào (1) ta có
2
x . Do đó nghiệm của hệ là
1 1
; ; 2; ;0 , 2; ;0
2 2
x y z
0,25
II
2điểm
II.1 (1 điểm)
Nhận xét. Nếu 0 , 0 ;
2
x y
x y
thì
sin sin 2 sin cos 2sin
2 2 2
x y x y x y
x y
. Dấu bằng xảy ra khi
x y
0,25
Sử dụng nhận xét trên ta có
4
sin sin sin sin 2 sin 2sin
3 2 6
4
2 6
4sin 4sin
2 3
A B C A B A B C
A B C
A B A B C
A B C
0,5
sin sin sin 3sin
3
A B C
A B C
. Dấu bằng xảy ra khi
A B C
. 0,25
II.2 (1 điểm)
Đặt
,
3
B C D
t
ta có
2
2 3 ; 1
3 3
A t t
0,25
Khi đó theo phần II.1 ta có
2 3 3 5
sin 3sin cos sin
3 2 2
t
P t t t
0,25
Khi đó
22
2 2
3 5
sin cos 7
2 2
P t t
0,25
Đẳng thức xảy ra khi
3 5
cos ; sin 2
28 28
t t
Vậy
max 7 , 2 3
P B C D t A t
(với
t
xác định bởi (1) và (2))
0,25
III
1điểm
+) Trước hết ta tính n(A). Với số tự nhiên có tám chữ số đôi một khác nhau
thì chữ số đầu tiên có 9 cách chọn và có
7
9
A
cho 7 vị trí còn lại. Vậy
7
9
9
n A A
0,25
+) Giả sử
0;1;2;...;9
B ta thấy tổng các phần tử của B bằng
45 9
nên số có
chín chữ số đôi một khác nhau và chia hết cho 9 sẽ được tạo thành từ 8 chữ
số đôi một khác nhau của các tập
\ 0; 9 ; \ 1; 8 ; \ 2; 7 ; \ 3; 6 ; \ 4; 5
B B B B B
nên số các số loại này là
8 7
8 7
4.7.
A A
.
0,5
Vậy xác suất cần tìm là
8 7
8 7
7
9
4.7.
1
9. 9
A A
A
.
0,25
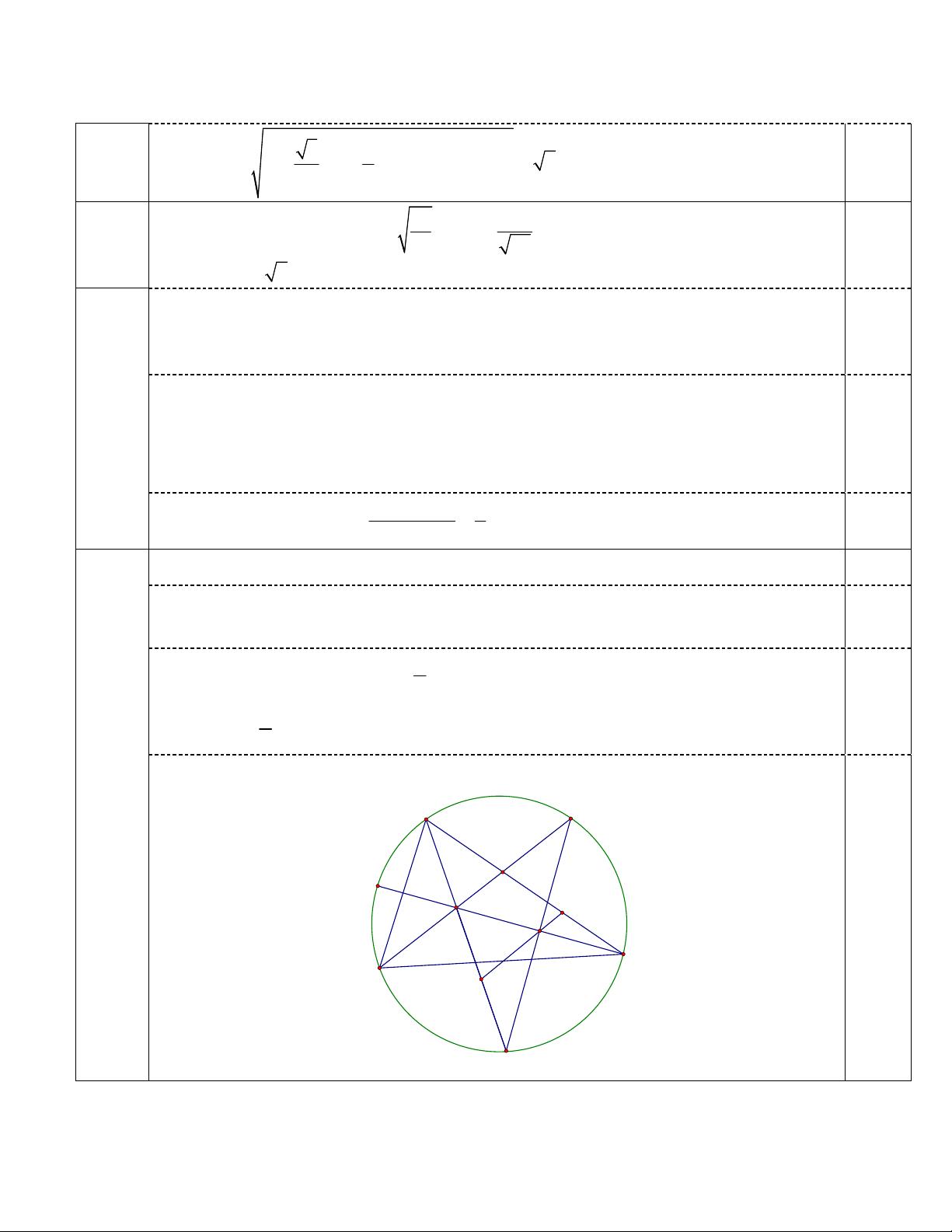
IV
2điểm
* Dễ thấy
฀
0
1
90
IPC , do đó O là trung điểm của
1
IC
. 0,5
*
฀
฀
฀
฀
1 1 1
2 //
IOP IC P CAB CC B BC OP
* Do BM=MN; 1 1
//
OI OC IN C B
0,5
Do đó
฀
฀
1
CIA BAC
, mà
฀
฀
฀
1
1
2
CIA BAC ACB
Vậy
฀ ฀
฀
฀
฀
1
2
BAC BAC ACB BAC ACB
0,5
Cùng với
฀
฀
2
BAC ABC
ta được
฀
฀
฀
0 0
72 ; 36
BAC ACB ABC
M
O
I
N
P
A
1
B
1
C
1
A
B
C
0,5
V
1điểm
1
(3 ) (2 ) 2 (1)
2
f x f f x x
Từ (1) suy ra 1 2 2 2
( ) ( ) , 0
2 3 3 3
x x x
f x f f f x x
(2)
0,25
Khi đó
1 2 2 2 1 2 2 1 2 2 4 2
( ) .
2 3 3 3 2 3 3 3 3 3 27 3
x x x x x x
f x f f f f x
Xét dãy
( )
n
a
, (n=1,2,…) được xác định như sau: 1
2
3
a
và 2
1
1 2
3 3
n n
a a
.
0,25
Ta sẽ chứng minh bằng quy nạp theo n rằng với mỗi
*
n
฀
luôn có
( )
n
f x a x
với
0
x
(3)
Thật vậy, khi
1
n
thì theo (2), ta có ngay (3)
Giả sử mệnh đề (3) đúng với
n k
. Khi đó
1
1 2 2 1 2 2 1 2 2
( ) . . .
2 3 3 2 3 3 2 3 3
22. .
3
k
x x x x x x
f x f f a f a a
k k k
akx a x
Vậy (3) đúng với
1
n k
.
0,25
Tiếp theo ta chứng minh
lim 1
n
a
. Thật vậy, ta thấy ngay
*
1
n
a n
฀
. Do
đó: 1
1
( 1)( 2) 0
3
n n n n
a a a a
, suy ra dãy
( )
n
a
tăng ngặt.
Dãy
( )
n
a
tăng và bị chặn trên nên hội tụ. Đặt lim n
a l
thì 2
1 2
3 3
l l
với
1
l
,
suy ra
1
l
. Vậy
lim 1
n
a
.Do ®ã tõ (3) suy ra
( )
f x x
víi mäi
0
x
(®pcm).
0,25