36 5 .
x y
A
= −
(Đ thi này có 5 bài, g m 01 trang)ề ồ
Bài 1: (4,0 đi m)ể
Cho bi u th c: ể ứ
( )
2
2 1
2.
1 1
x
x x x x
Px x x x
−
− +
= − +
+ + −
a. Rút g n P.ọ
b. Tìm giá tr nh nh t c a P.ị ỏ ấ ủ
c. Xét bi u th c: ể ứ
2,
x
QP
=
ch ng t 0 < Q < 2.ứ ỏ
Bài 2: (4,5 đi m) ể
a. Không dùng máy tính hãy so sánh :
2014 2015
2015 2014
+
và
2014 +
2015
.
b. Tìm x, y, z, bi t: 4xế2 + 2y2 + 2z2 – 4xy – 2yz + 2y – 8z + 10
0
.
c. Gi i ph ng trình: ả ươ
1 5 4.
3 4x x
+ =
+ +
Bài 3: (4,0 đi m) ể
a. V i ớ
Tính giá tr c a bi u th c: B = ị ủ ể ứ
( )
2015
3 2
3 8 2x x+ −
.
b. Tìm t t c các c p s nguyên (x ; y) v i x > 1, y > 1 sao cho ấ ả ặ ố ớ
(3x+1)
M
y đng th i (3y + 1) ồ ờ
M
x.
Bài 4: (6,0 đi m) ể
Cho tam giác ABC có ba góc nh n v i các đng cao AD, BE, CF c t nhau t iọ ớ ườ ắ ạ
H.
a. Ch ng minh r ng: ứ ằ
Tam giác
AEF
đng d ng v i tam giácồ ạ ớ
ABC
;
2
cos .
AEF
ABC
SA
S=
b. Ch ng minh r ng :ứ ằ
( )
222
1 cos cos cos .
DEF ABC
S A B C S= − − −
c. Cho bi t AH = k.HD. Ch ng minh r ng: tanB.tanC = k + 1. ế ứ ằ
d. Ch ng minh r ng: ứ ằ
3
HA HB HC
BC AC AB
+ +
.
Bài 5: (1,5 đi m) ể
Cho x, y là các s t nhiên khác 0, tìm giá tr nh nh t c a bi u th c: ố ự ị ỏ ấ ủ ể ứ
H tế
H tên thí sinh:................................................ Ch kí c a giám th :1:...................ọ ữ ủ ị
S báo danh:................. Ch kí c a giám th 2:...................ố ữ ủ ị
PHÒNG GIÁO D C & ĐÀO T OỤ Ạ
HUY N HO NG HOÁỆ Ằ
Đ THI H C SINH GI I L P 9Ề Ọ Ỏ Ớ
NĂM H C 2014-2015Ọ
MÔN THI: TOÁN
Ngày thi: 21/10/2014
Th i gian: 150 phút ( Không k th i gian giao đ)ờ ể ờ ề
Giám th không gi i thích gì thêmị ả
PHÒNG GIÁO D C & ĐÀO T OỤ Ạ
HUY N HO NG HOÁỆ Ằ H NG D N THI H C SINH GI I L PƯỚ Ẫ Ọ Ỏ Ớ
9
NĂM H C 2014-2015Ọ
MÔN : TOÁN
H ng d n ch m này có 03 trangướ ẫ ấ
I. Yêu c u chung: ầ
1. H c sinh gi i b ng cách khác đúng v n cho đi m t i đa t ng ng.ọ ả ằ ẫ ể ố ươ ứ
2. Bài hình h c sinh không v hình ho c v hình sai c b n thì không choọ ẽ ặ ẽ ơ ả
đi m.ể
II. Yêu c u c th : ầ ụ ể
Bài N i dung c n đtộ ầ ạ Đi mể
1a.(2,0đ) Đk :
0; 1.x x>
( ) ( ) ( ) ( )
( ) ( ) ( )
1 2 1 2 1 1
1 1
1 2 1 2 1
1
x x x x x x x
Px x x x
x x x x
x x
− + + −
= − +
+ + −
= − − + + +
= − +
V y ậ
1P x x= − +
, v i ớ
0; 1.x x>
0,25
0,5
0,5
0,5
0,25
b. (1,0đ)
2
1 3 3
12 4 4
P x x x
� �
= − + = − +
� �
� �
d u b ng x y ra khi x = ¼, th a mãn đk.ấ ằ ả ỏ
V y GTNN c a P là ậ ủ
3
4
khi
1
4
x=
.
0,25
0,5
0,25
c. (1,0đ).V i ớ
0; 1x x>
thì Q =
2
1
x
x x− +
> 0. (1)
Xét
( )
2
2 1
2
2 0
1 1
x
x
x x x x
−
− =
− + − +
D u b ng không x y ra vì đi u ki n ấ ằ ả ề ệ
1x
.
suy ra Q < 2.(2)
T (1) và (2) suy ra 0 < Q < 2.ừ
0,25
0,25
0,25
0,25
2
2014 2015 2015 1 2014 1
2015 2014 2015 2014
1 1
2015 2014 2015 2014
2014 2015
− +
+ = +
= + + − > +
V y ậ
2014 2015
2015 2014
+
>
2014 +
2015
.
0,5
0,75
0,25
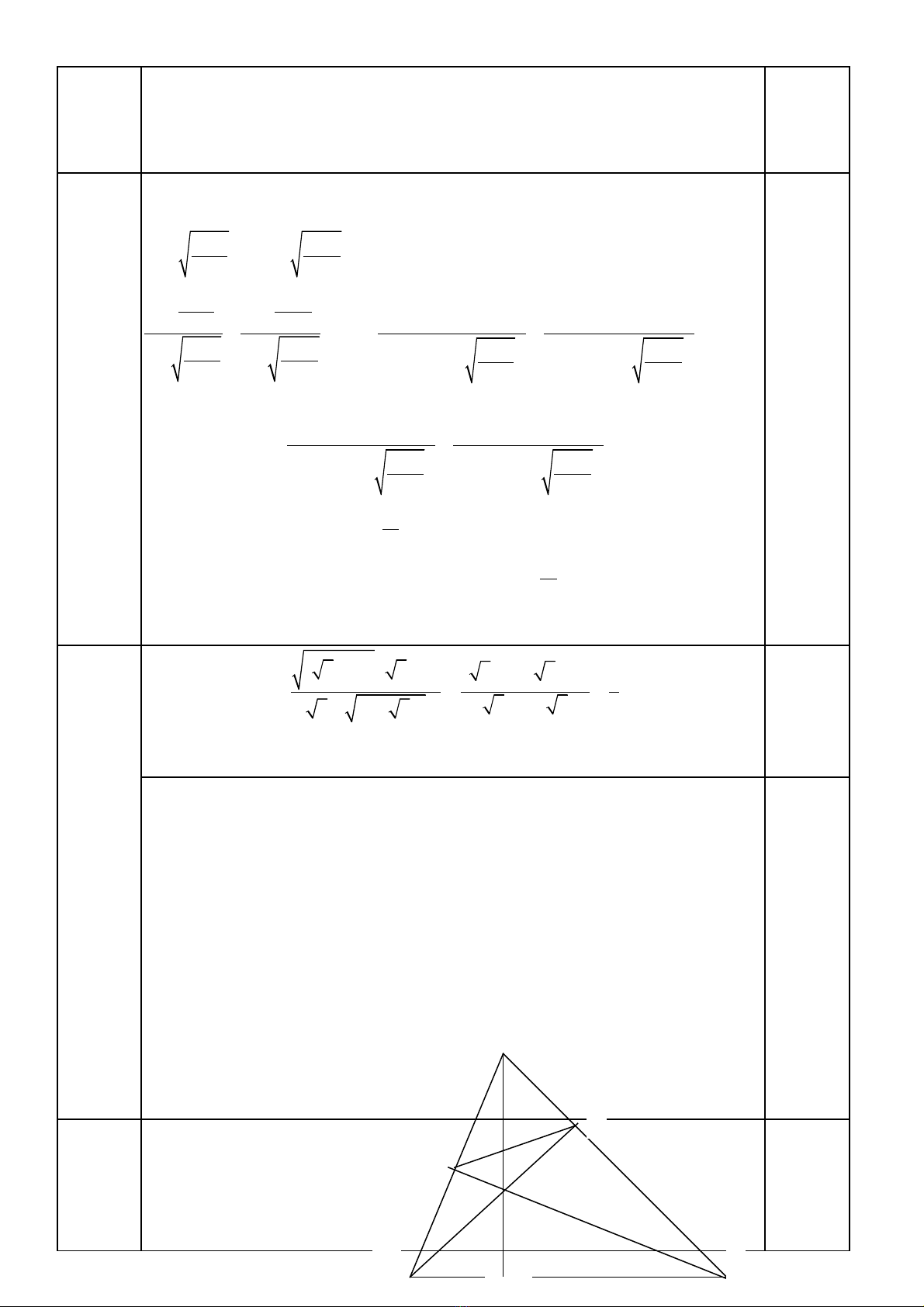
b. Phân tích đc thành (2x - y)ượ 2 + (y – z + 1)2 + ( z -
3)2
0
(1)
Vì (2x - y)2
0
; (y – z + 1)2
0
; ( z - 3)2
0
v i m i x, y, z nên tớ ọ ừ
(1) suy ra x = 1; y = 2; z = 3.
0,75
0,75
c. Đk: x > - 3.
Khi đó ph ng trình đã cho t ng đng v i ươ ươ ươ ớ
1 5
2 2 0
3 4x x
� � � �
− + − =
� � � �
� � � �
+ +
� � � �
( ) ( )
1 5
4 4 4 11 4 11
3 4 0 0
1 5 1 5
2 2 3 2 4 2
3 4 3 4
x x
x x
x x
x x x x
− − + +
+ +
+ = + =�� � � �
+ + + + + +
� � � �
+ + + +
� � � �
Vì x > - 3 nên
( ) ( )
1 1 0
1 5
3 2 4 2
3 4
x x
x x
+ >
� � � �
+ + + +
� � � �
+ +
� � � �
Do đó 4x + 11 = 0
x =
11
4
−
th a mãn đi u ki n. ỏ ề ệ
V y t p nghi m c a ph ng trình là: ậ ậ ệ ủ ươ
11
4
S� �
= −
� �
�
.
0,25
0,5
0,25
0,25
0,25
3
a. Ta có
( ) ( ) ( ) ( )
3
3
2
5 2 5 2 5 2 5 2 1.
3
5 3 5
5 (3 5)
x
− + − +
= = =
+ −
+ −
Do đó B = - 1.
1,25
0,75
b. D th y ễ ấ
x y
. Không m t tính t ng quát, gi s x > y.ấ ổ ả ử
T (3y + 1) ừ
M
x
( )
*
3 1 . .y p x p N+ =� �
Vì x > y nên 3x > 3y + 1 = p.x.
p < 3. V y pậ
{ }
1;2
V i p = 1: ớ
x = 3y + 1
3x + 1 = 9y + 4
M
y
4
M
y
Mà y > 1 nên y
{ }
2;4
+ V i y = 2 thì x = 7.ớ
+ V i y = 4 thì x = 13.ớ
V i p = 2: ớ
2x = 3y + 1
6x = 9y + 3
2(3x + 1) = 9y + 5
Vì 3x + 1
M
y nên 9y + 5
M
y suy ra 5
M
y , mà y > 1 nên y = 5,
suy ra x = 8.
T ng t v i y > x ta cũng đc các giá tr t ng ng.ươ ự ớ ượ ị ươ ứ
V y các c p (x; y) c n tìm là: (7;2);(2;7);(8;5);(5;8);(4;13);(13;4);ậ ặ ầ
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
4a.
A
BC
F
E
H
D
Tam giác ABE vuông t i E nên cosA = ạ
AE
AB
Tam giác ACF vuông t i F nên cosA = ạ
AF
AC
.
Suy ra
AE
AB
=
AF
AC
( . . )AEF ABC c g c∆ ∆:
* T ừ
AEF ABC∆ ∆:
suy ra
2
2
cos
AEF
ABC
S AE A
S AB
� �
= =
� �
� �
0,25
0,25
0,25
0,75
b. T ng t câu a, ươ ự
2 2
cos , cos .
CDE
BDF
ABC ABC
S
SB C
S S
= =
T đó suy raừ
2 2 2
DEF
1 cos cos cos
ABC AEF BDF CDE
ABC ABC
S S S S
SA B C
S S
− − −
= = − − −
Suy ra
( )
222
1 cos cos cos .
DEF ABC
S A B C S= − − −
0,5
0,75
0,25
c. Ta có: tanB =
AD
BD
,tanC =
AD
CD
. Suy ra tanB.tanC =
2
.
AD
BD CD
Vì AH = k.HD
( )
1 .AD AH HD k HD= + = +�
nên
( )
2
2 2
1 .AD k HD= +
(1)
Do đó tanB.tanC =
( )
2
2
1
.
HD k
BD CD
+
(2)
L i có ạ
( . )DHB DCA g g∆ ∆:
nên
. .
DB HD DB DC HD AD
AD DC
= =�
(3)
T (1), (2), (3) suy ra: ừ
tanB.tanC =
( ) ( ) ( )
( )
2 2 2
2
1 1 1 1.
. 1
HD k HD k HD k k
AD HD AD HD k
+ + +
= = = +
+
0,25
0,25
0,25
0,25
0,5
d. T ừ
. .
AF . .
HBC
ABC
S
HC CE HC HB CE HB
C HEC AC CF AC AB CF AB S
∆ ∆ = = =� �:
T ng t : ươ ự
.
.
HAB
ABC
SHB HA
AC BC S
=
;
.
.
HAC
ABC
S
HA HC
AB BC S
=
. Do đó:
.
.
HC HB
AC AB
+
.
.
HB HA
AC BC
+
.
.
HA HC
AB BC
=
1
HBC HCA HAB
ABC
S S S
S
+ + =
Ta ch ng minh đc: (x + y + z)ứ ượ 2
3(xy + yz + zx) (*)
Áp d ng (*) ta có:ụ
2
. . .
3. 3.1 3
. . .
HA HB HC HA HB HB HC HC HA
BC AC AB BC BA CA CB AB AC
� � � �
+ + + + = =
� � � �
� � � �
Suy ra
3
HA HB HC
BC AC AB
+ +
.
0,25
0,25
0,25
0,25
0,25
0,25
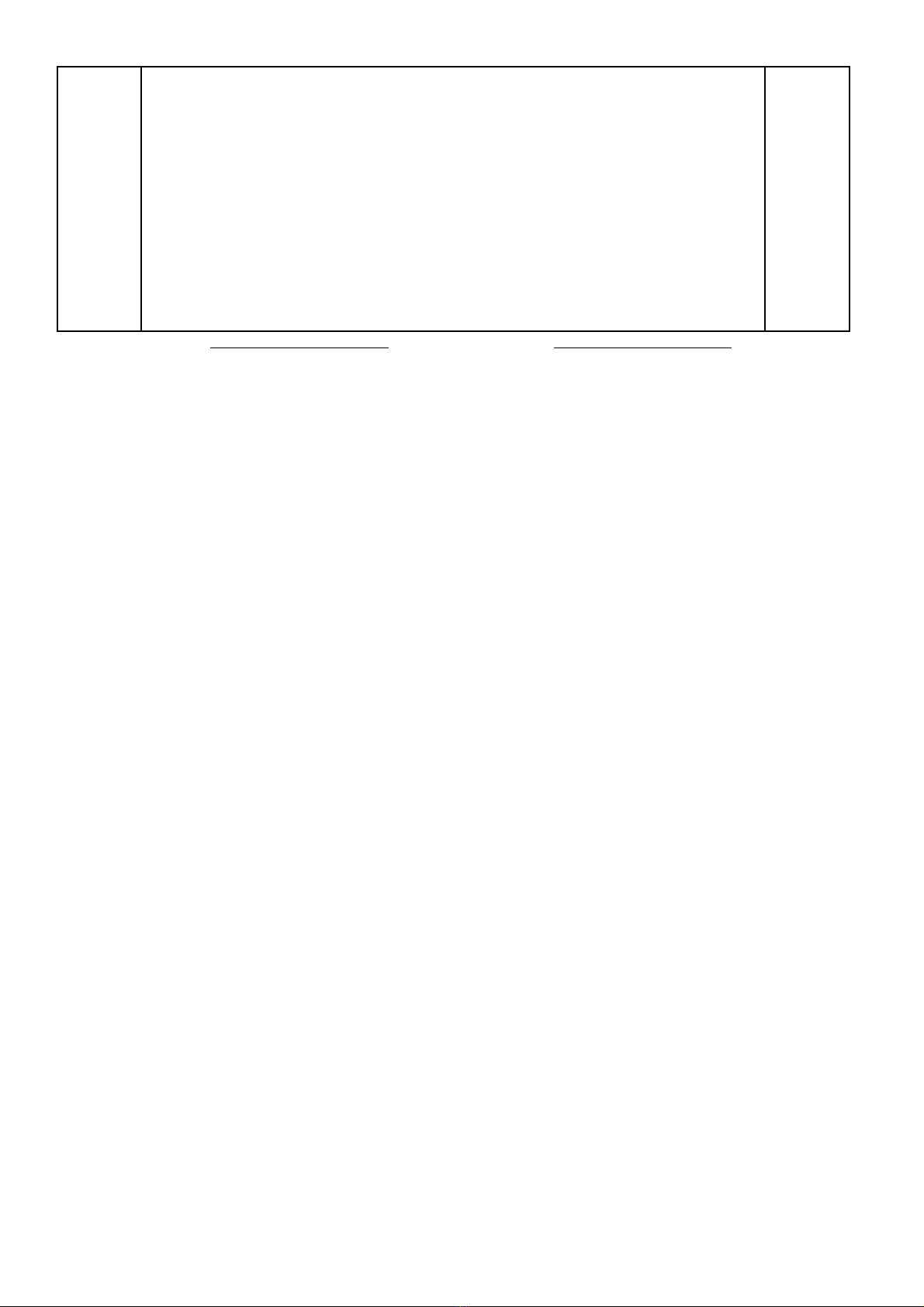
5V i ớ
*
,x y N
thì 36x có ch s t n cùng là 6, 5ữ ố ậ y có ch s t nữ ố ậ
cùng là 5 nên :
A có ch s t n cùng là 1 ( n u 36ữ ố ậ ế x > 5y) ho c 9 ( n u 36ặ ế x < 5y)
TH1: A = 1. khi đó 36x - 5y =1
36x - 1 = 5y . Đi u này khôngề
x y ra vì (36ảx – 1)
M
35 nên (36x – 1)
M
7, còn 5y không chia h tế
cho 7.
TH2: A = 9. Khi đó 5y - 36x = 9
5y = 9 + 36x đi u này khôngề
x y ra vì (9 + 36ảx)
M
9 còn còn 5y không chia h t cho 9.ế
TH3: A = 11. Khi đó 36x - 5y =11. Th y x = 1, y = 2 th a mãn.ấ ỏ
V y GTNN c a A b ng 11, khi x = 1, y = 2.ậ ủ ằ
0,25
0,25
0,25
0,25
0,25
0,25
H tế
Ng i làm đáp án: Ng i th m đnh:ườ ườ ẩ ị
1. ................................................... ........................................
2. ................................................... Ng i duy t:ườ ệ