Đề thi KSCL môn Toán lớp 9 năm 2021-2022 có đáp án - Trường THCS Hồng Hà, Đan Phượng

Chia sẻ: _ _ | Ngày: | Loại File: DOCX | Số trang:6

Thêm vào BST

Báo xấu

13
lượt xem 2
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Các bạn hãy tham khảo và tải về “Đề thi KSCL môn Toán lớp 9 năm 2021-2022 có đáp án - Trường THCS Hồng Hà, Đan Phượng” sau đây để biết được cấu trúc đề thi cũng như những nội dung chính được đề cập trong đề thi để từ đó có kế hoạch học tập và ôn thi một cách hiệu quả hơn. Chúc các bạn thi tốt!

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Đề thi KSCL môn Toán lớp 9 năm 2021-2022 có đáp án - Trường THCS Hồng Hà, Đan Phượng

PHÒNG GDĐT ĐAN PHƯỢNG ĐỀ KIỂM TRA KHẢO SÁT CHẤT LƯỢNG TRƯỜNG THCS HỒNG HÀ NĂM HỌC: 2021 - 2022 MÔN: TOÁN 9 Thời gian: 120 phút Bài I. (2,0 điểm) Cho hai biểu thức: và với. 1) Tính giá trị biểu thức A khi ; 2) Chứng minh ; 3) Tìm các giá trị nguyên của x để biểu thức đạt giá trị lớn nhất. Bài II. (2,5 điểm) 1) Giải bài toán bằng cách lập phương trình hoặc hệ phương trình Để hưởng ứng phong trào phòng chống Covid-19, một chi đoàn thanh niên dự định làm 600 mũ ngăn giọt bắn trong một thời gian quy định. Nhờ tăng năng suất lao động mỗi giờ chi đoàn đó làm được nhiều hơn so với dự định là 30 chiếc nên công việc đã hoàn thành sớm hơn quy định 1 giờ. Hỏi theo dự định mỗi giờ chi đoàn làm bao nhiêu chiếc mũ ngăn giọt bắn? 2) Tính diện tích nhựa cần dùng để làm một chiếc hộp có dạng hình trụ. Biết chiếc hộp dựng vừa khít ba quả bóng bằng nhau có dạng hình cầu và đường kính của quả bóng là 6cm (như hình vẽ). (Bỏ qua bề dày của nhựa và phần ghép nối. Kết quả làm tròn đến cm2) Bài III. (2,0 điểm) 1) Giải hệ phương trình sau: 2) Trong mặt phẳng tọa độ Oxy, cho parabol (P): y = x 2 và đường thẳng (d): y = - 4x + m2 – 4. a) Tìm m để (d) cắt (P) tại hai điểm phân biệt có hoành độ x1, x2; b) Tìm các giá trị của m để x1= x23 + 4x22. Bài IV. (3,0 điểm) Cho đường tròn (O; R) có hai đường kính AB và CD vuông góc với nhau. Gọi M là một điểm di động thuộc cung nhỏ BC (M không trùng B, C). Kẻ CH vuông góc với AM tại H. 1) Chứng minh bốn điểm A, O, H, C cùng thuộc một đường tròn; 2) Gọi K là hình chiếu của M trên CD. Chứng minh rằng: OH // MD và H là tâm đường tròn nội tiếp tam giác MOK; 3) Gọi F là giao điểm của MD và AB, N là giao điểm của AM và CD. Chứng minh DF.DM = ND.AF = 2R2 và tìm vị trí của điểm M để diện tích tam giác MNF lớn nhất. Bài V. (0,5 điểm) Cho a, b, c là các số dương thỏa mãn ab + bc = 2ac. Tìm giá trị nhỏ nhất của biểu thức: ---------Hết--------- ĐÁP ÁN VÀ HƯỚNG DẪN CHẤM MÔN TOÁN KHẢO SÁT CHẤT LƯỢNG LẦN 2 NĂM HỌC 2020 - 2021
Bài Ý Đáp án Điểm 1 0,25 0,25 Thay x = 16(TMĐK) Tính đúng 2 0,25 Bài I (2,0 đ) 0,25 0,25 0,25 3 Ta có : 0,25 Lập luận P đạt GTLN đạt 0,25 GTLN dương nhỏ nhất. Vì x Z nên x = 2. Vậy GTLN của khi x = 2.
1 Gọi số chiếc mũ 0,25 mà chi đoàn dự 0,25 định làm mỗi giờ là x (chiếc, x 0,25 N* ) 0,25 Thời gian chi đoàn hoàn thành 0,25 công việc theo dự định là: (giờ) Thực tế mỗi giờ 0,5 đoàn làm được số chiếc mũ là : x + 0,25 30 (chiếc) Thời gian chi đoàn hoàn thành công việc theo thực tế là : (giờ) Vì thực tế chi đoàn hoàn thành sớm hơn dự định 1 giờ nên ta có Bài II (2,5 đ) pt: -= 1 Giải pt tìm ra được x = 120 (TMĐK) và y = -150 (TMĐK) Vậy mỗi giờ chi đoàn dự định làm 120 chiếc mũ ngăn giọt bắn. 2 Hình trụ có bán kính đáy là r = 6 : 0,5 2 = 3cm, chiều cao là: h = 6.3 = 18cm. Diện tích nhựa cần dùng để làm chiếc hộp là: S = 2r2 + 2 r.h = 2 .32 + 2 .3.18 369 cm2
1 ĐK: . Đặt , . ĐK a ≥ 0, b ≠ 0. 0,25 Hệ pt đã cho trở thành 0,25 Giải hpt được Suy ra được: 0,25 Vậy hpt có nghiệm 0,25 2a Xét pt hoành độ giao điểm của (d) và (P): 0,25 Ta có ∆’ = 22 – 1. (- m2 + 4) = 4 + 0,25 Bài III (2,0 đ) m2 – 4 = m2 (d) cắt (P) tại hai điểm phân biệt có hoành độ x1, x2 pt (*) có hai nghiệm phân biệt x1, x2 ∆’ > 0 m2 > 0 m ≠ 0. 2b Theo ĐL Vi-ét ta có: Theo bài ra ta có: x1= x23 + 4x22 thay vào (1) ta 0,25 được: Suy ra được: x1 = 0. 0,25 Thay x1 = 0, vào (2) ta được: m2 = 4 m= 2 (TMĐK) Vậy m = 2
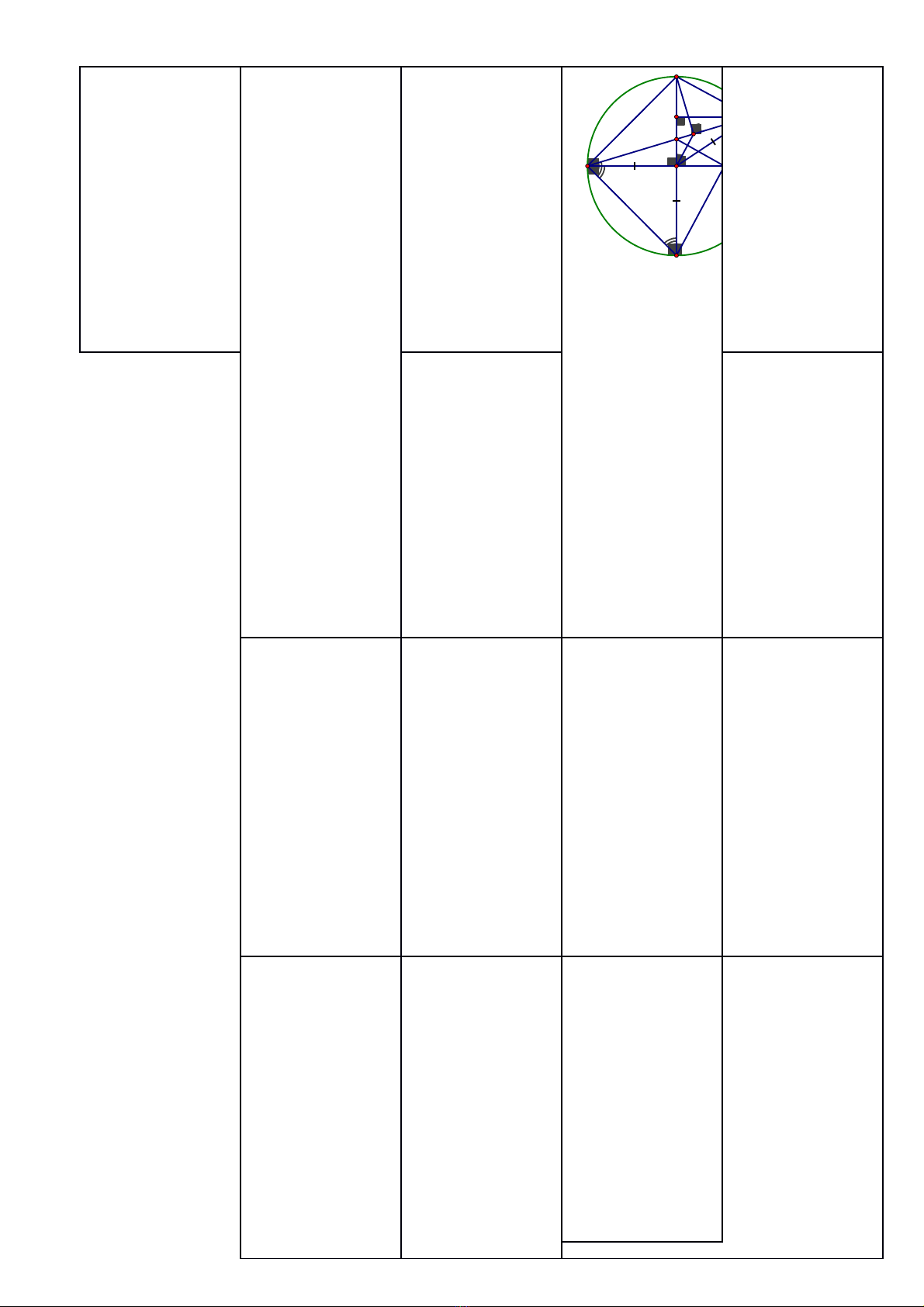
C Bài IV (3,0 đ) 1 Vẽ được hình 0,25 đến câu 1 K M N H A B O F D Chứng minh 0,75 được 4 điểm A, O, H, C cùng thuộc một đường tròn 2 Chứng minh 0,25 được: 0,25 Suy ra OH // 0,25 MD 0,25 C/m được OH là tia phân giác của C/m được MH là tia phân giác của Kết luân được H . là tâm đường tròn nội tiếp tam giác MOK 3 Xét ∆AND và ∆FDA, có: 0,25 0,25 0,25 Từ đó suy ra DF.DM = được: ND.AF = 2R2
Ta có 0,25 Diện tích tam giác MNF lớn nhất khi diện tích tam giác AMD lớn nhất  M là điểm chính giữa của cung nhỏ BC. Với a, bc, c > 0, ta có ab + bc = 2ac Thay vào P ta được: Dấu “=” xảy ra khi a = b = c. Vậy min P = 4 khi a = b = c Bài V (0,5 đ) 0,25 0,25 - Điểm toàn bài làm tròn đến chữ số thập phân thứ hai. - Học sinh làm cách khác đúng cho điểm tương đương điểm tương đương.