Đề thi KSCL môn Toán lớp 9 năm 2023-2024 có đáp án - Trường THCS Ái Mộ (Tháng 12)

Chia sẻ: _ _ | Ngày: | Loại File: DOC | Số trang:4

Thêm vào BST

Báo xấu

4
lượt xem 1
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Tham khảo “Đề thi KSCL môn Toán lớp 9 năm 2023-2024 có đáp án - Trường THCS Ái Mộ (Tháng 12)” để giúp các em làm quen với cấu trúc đề thi, đồng thời ôn tập và củng cố kiến thức căn bản trong chương trình học. Tham gia giải đề thi để ôn tập và chuẩn bị kiến thức và kỹ năng thật tốt cho kì thi sắp diễn ra nhé!

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Đề thi KSCL môn Toán lớp 9 năm 2023-2024 có đáp án - Trường THCS Ái Mộ (Tháng 12)

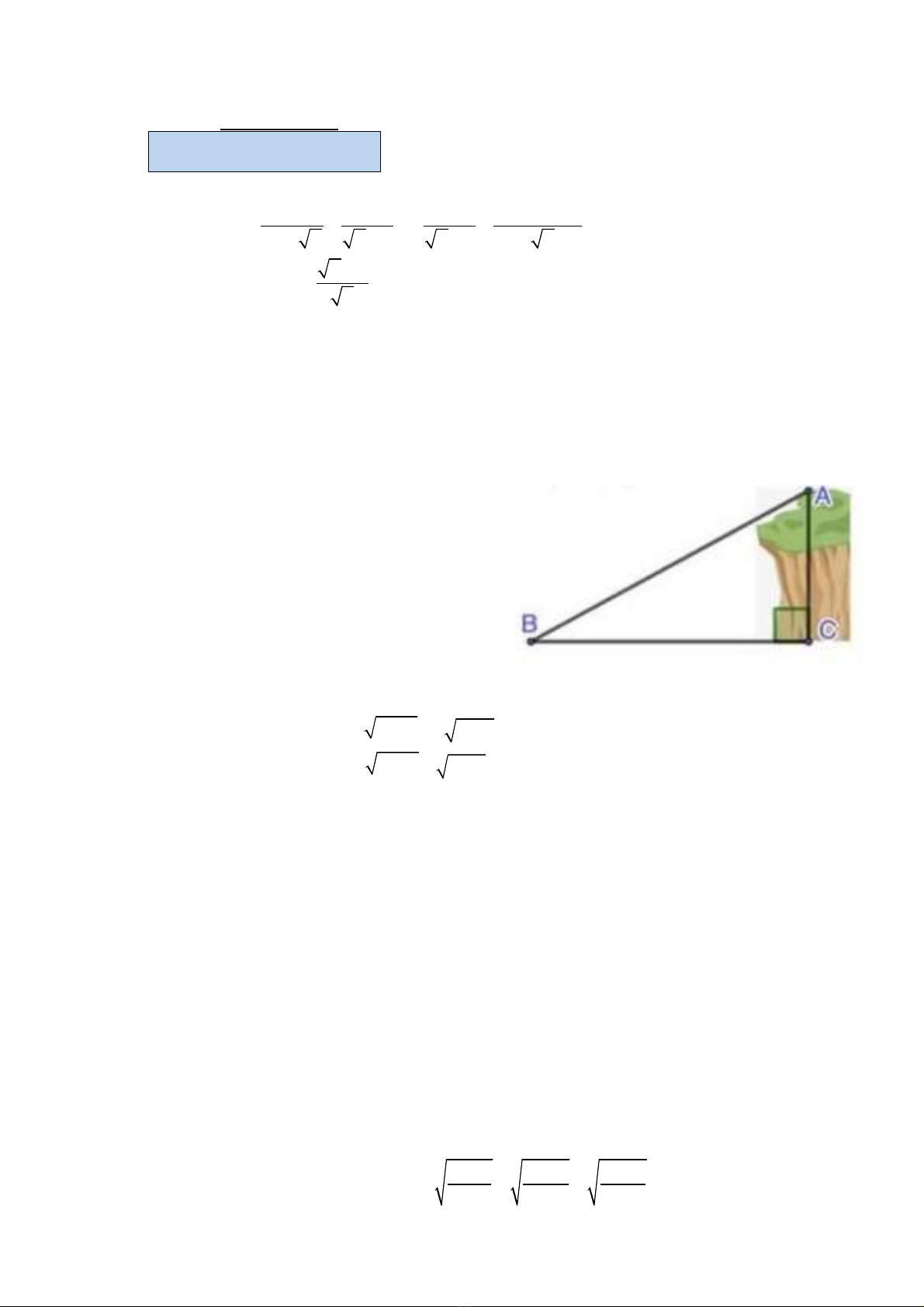
TRƯỜNG THCS ÁI MỘ ĐỀ LUYỆN KHẢO SÁT THÁNG 12 LỚP 9B MÔN: TOÁN 9 NĂM HỌC: 2023 - 2024 Thời gian làm bài: 90 phút ĐỀ LUYỆN SỐ 1 Bài I. (2,0 điểm) Cho biểu thức: 2 1 1 4 A= + : + với x > 0, x 4 . x−2 x x −2 x −2 x −4 x +4 x −2 a) Chứng minh A = x b) Tính giá trị của A khi x = 49 . c) So sánh A với 2. Bài II. (2,5 điểm) Bài toán liên quan đến ứng dụng toán học vào thực tế 1. Giải bài toán bằng cách lập hệ phương trình hoặc hệ phương trình: Lúc 6 giờ 30 phút sáng, một cano xuôi dòng sông từ A đến B dài 48km. Khi đến B, cano nghỉ 30 phút sau đó lại ngược dòng từ B về đến A lúc 10 giờ 36 phút cùng ngày. Tìm vận tốc riêng của cano, biết vận tốc dòng nước là 3km/h. 2. Để nhìn thấy đỉnh A của vách đá dựng đứng, người ta đứng tại B cách chân vách đá khoảng 45m và nhìn lên một góc 250 so với phương ngang. Tính chiều cao của vách đá (làm tròn 0 hàng đơn vị)? đến 25 Bài II. (2 điểm) 3 x2 + 1 − 2 y − 7 = 4 1. Giải hệ phương trình sau : 2 x2 + 1 + y − 7 = 5 2. Cho đường thẳng (d): y = ( m − 2 ) x + m − 1 a) Tìm m để đường thẳng (d) song song với đường thẳng (d1): y = x + 3 . Vẽ đường thẳng (d) với m vừa tìm được và tính diện tích tam giác tạo bởi (d) và hai trục tọa độ. b) Tìm m để đường thẳng (d) cắt trục hoành tại điểm có hoành độ bằng 2. c) Tìm m để đường thẳng (d) cắt đường thẳng y = 2x − 1 tại điểm có hoành độ bằng −2 . Bài IV. (3,0 điểm) Cho tam giác ABC có ba góc nhọn (AB < AC), đường cao BF và CE của tam giác cắt nhau tại H. a) Chứng minh rằng bốn điểm B, E, F, C cùng thuộc một đường tròn. Xác định tâm O của đường tròn đó. b) Chứng minh AB.CE = AC.BF. c) Gọi I là trung điểm của AH. Chứng minh rằng OI ⊥ EF . d) Chứng minh rằng IF là tiếp tuyến của đường tròn ( O ) . Bài V. (0,5 điểm) Cho a, b, c là ba số thực dương thỏa mãn điều kiện a + b + c = 1. ab bc ca Tìm giá trị lớn nhất của biểu thức: P = + + . c + ab a + bc b + ca ……………….Chúc em làm bài tốt…………………..
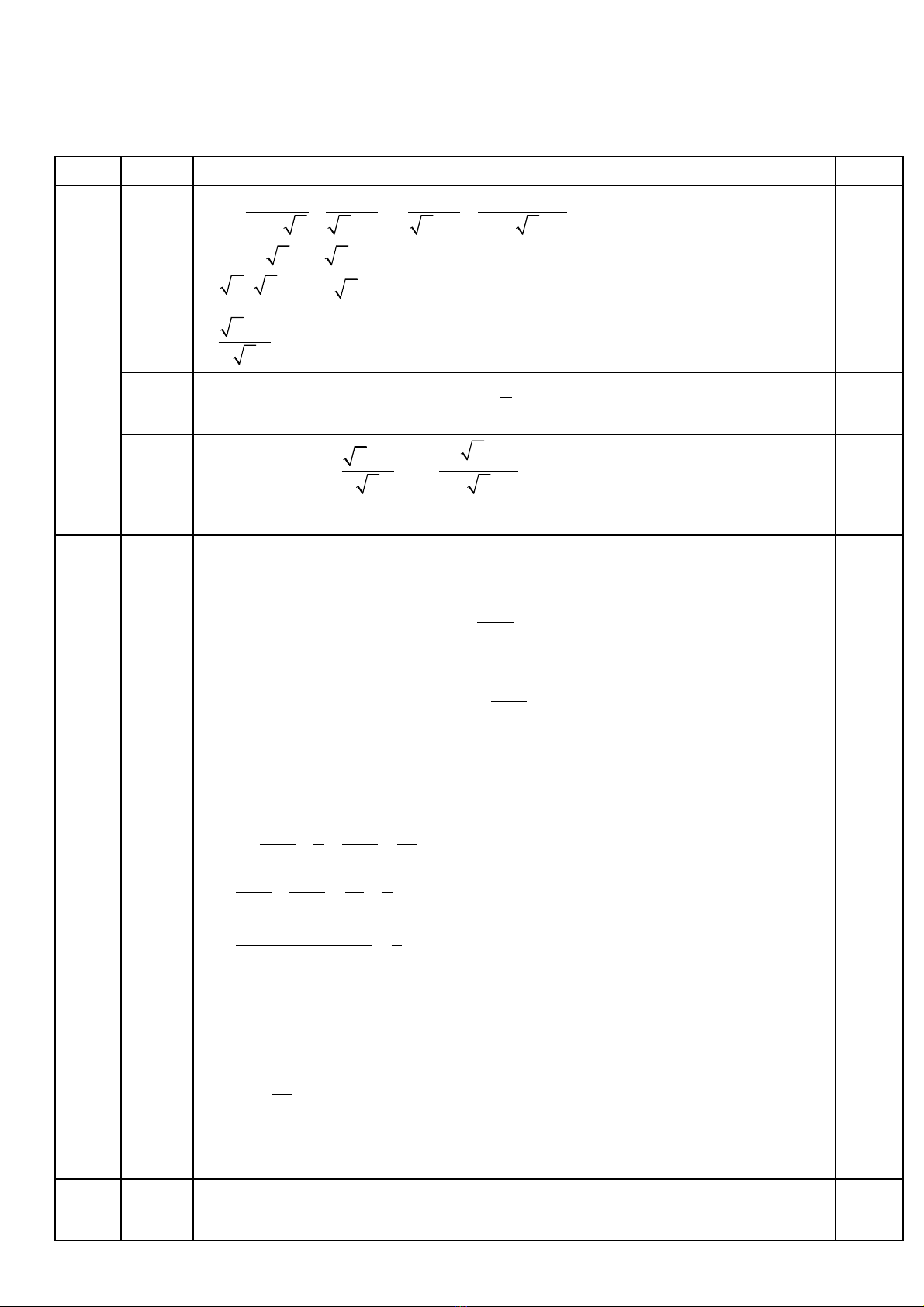
TRƯỜNG THCS ÁI MỘ ĐỀ LUYỆN KHẢO SÁT THÁNG 1 NĂM HỌC 2023-2024 MÔN TOÁN 9 – Thời gian làm bài 90 phút Bài Câu Nội dung Điểm 2 1 1 4 A= + : + x−2 x x −2 x −2 x−4 x +4 a 2+ x x −2+4 0,5 = : 1 x ( x −2 ) ( x −2 ) 2 x −2 0,5 1 = x 2,0đ b 5 0,5 Thay x = 49(tmđk), tính được A = (Thiếu tmđk trừ 0,25) 7 0,5 − ( x + 2) c Xét hiệu A − 2 = x − 2 − 2 = x x 0,25 0,5 Lập luận được A < 2 0,25 Gọi vận tốc riêng của cano là x ( x > 3, km / h ) 0,25 Vận tốc của cano khi xuôi dòng là x + 3 ( km / h ) 48 0,25 Thời gian của cano khi xuôi dòng là ( h) x+3 0,25 Vận tốc của cano khi ngược dòng là x − 3 ( km / h ) 48 0,25 Thời gian của cano khi ngược dòng là ( h) x −3 0,25 41 Vì tổng thời gian cano đi là 4 giờ 6 phút = h , thời gian cano nghỉ là 30 phút 0,5 10 1 0,25 = h , nên ta có phương trình: 2 2 2 48 1 48 41 + + = x + 3 2 x − 3 10 2,0đ 2,0 48 48 41 1 + = − x + 3 x − 3 10 2 8 ( x − 3) + 8 ( x + 3) 3 = ( x + 3) ( x − 3) 5 80 x = 3 x 2 − 27 3x 2 − 80 x − 27 = 0 ( 3x + 1) ( x − 27 ) = 0 −1 x= (ktm) 3 x = 27 (tm) Vậy vận tốc riêng của cano là 27 ( km / h ) . 3 a - Lập luận ra: m – 2 = 1 và m – 1 3 0,25 2đ 1 Tính được: m = 3(tmđk) 0,25
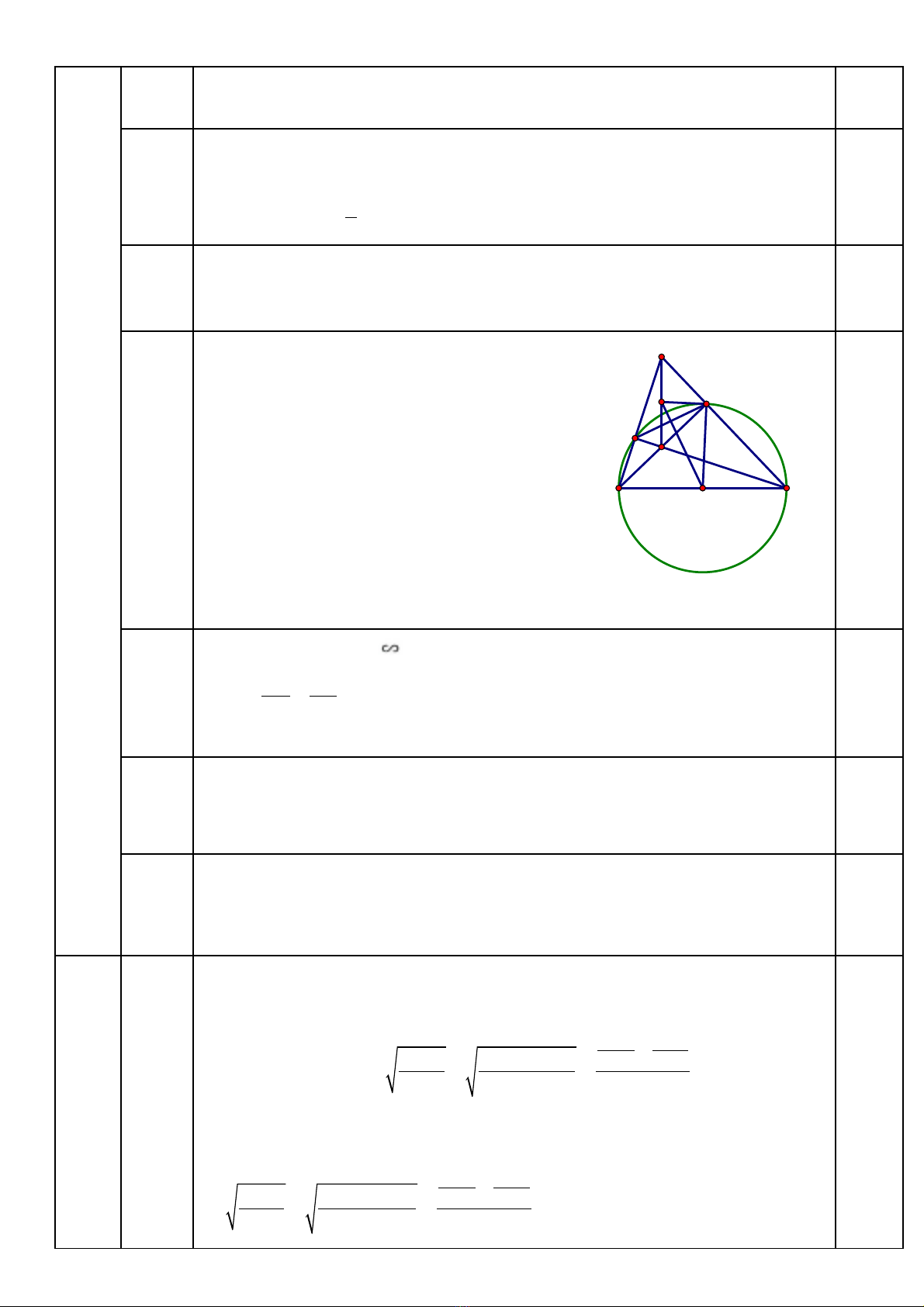
- Vẽ đúng (d) 0,25 - Tính đúng diện tích tam giác: 2 đvdt 0,25 Lập luận để thay x = 2; y =0 vào (d) có: 0,25 b 0 = (m-2).2 + m – 1 0,5 5 0,25 Tính đúng: m = 3 - Xét pt hoành độ giao điểm…,lập luận thay x = - 2 vào pt: 0,25 c Tính đúng được: m = 8 0,25 0,5 HS làm cách khác đúng- cho điểm tối đa Vẽ hình đúng đến câu a A 0,25 I F E H 4a 1,0đ B O C Chứng minh được bốn B, E, F, C cùng thuộc một đtròn. 0,75 Chứng minh ABF ACE (g.g) 0,5 4b AB BF 0,25 suy ra = 0,75đ AC CE suy ra AB.CE = AC.BF. 0,25 c/m: IE = IF => I thuộc đường trung trực của EF 0,25 4c O thuộc đường trung trực của EF 0,25 0,75đ suy ra OI là đường trung trực của EF OI EF 0,25 ? ? Chứng minh được OCF = OFC ; IAF = IFA ﾷﾷ 0,25 4d ﾷﾷﾷ lập luận được IFO = 180 − (OFC + IFA) = 180 − 90 = 90 0,25 0,75 suy ra IF ⊥ OF . Lập luận chỉ ra IF là tiếp tuyến của đường tròn ( O ) 0,25 5 5 Có: a + b + c = 1 c = ( a + b + c ) .c = ac + bc + c 2 0,5 0,5 ⇒ c + ab = ac + bc + c + ab = a (c + b) + c (b + c ) = (c + a)(c + b) 2 a b + Áp dụng bđt Côsi ⇒ ab = ab c+a c+b 0,25 c + ab (c + a )(c + b) 2 a + bc = (a + b)( a + c) Tương tự: b + ca = (b + c)(b + a ) b c + bc bc a+b a+c = a + bc (a + b)(a + c) 2
c a + ca ca b+c b+a = b + ca (b + c)(b + a) 2 a b b c c a a+c c +b b+a + + + + + + + 3 ⇒ P ≤ c + a c +b a +b a +c b +c b +a = a +c c +b b +a = 2 2 2 1 Dấu “=” xảy ra khi a = b = c = 0,25 3 HS giải theo cách khác vẫn cho điểm tối đa