TRƯỜNG THPT CHUYÊN NĐC ĐỀ THI THỬ ĐẠI HỌC VÀ CAO ĐẲNG NĂM 2014
-------------------------------- Môn: TOÁN; khối A-A
1
-B
ĐỀ THI THỬ LẦN 1 Thời gian làm bài: 180 phút, không kể phát đề
PHẦN CHUNG CHO TẤT CẢ THÍ SINH (7,0 điểm)
Câu 1 (2 điểm) Cho hàm số 262
3
++−= xxy có đồ thị là (C).
1) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.
2) Tìm
m
để đường thẳng
622:
+
−
=
mmxyd c
ắ
t
đồ
th
ị
(C) t
ạ
i ba
đ
i
ể
m phân bi
ệ
tCBA ,, sao cho t
ổ
ng h
ệ
s
ố
góc c
ủ
a các ti
ế
p tuy
ế
n v
ớ
i (C) t
ạ
i CBA ,, b
ằ
ng
6
−
.
Câu 2 (1 điểm)
Gi
ả
i ph
ươ
ng trình
x
xxx
xx
2
432
2
sin
1sin2sin7sin3
cot3sin ++−
=+
Câu 3 (1 điểm)
Gi
ả
i h
ệ
ph
ươ
ng trình
−=−−−++
=++−
12216244
02)2(
222
xyxx
xyxy
Câu 4 (1 điểm) Tính tích phân
( )
∫
+−=
2
1
ln1 dxxxxI
Câu 5
(1 điểm)
Cho hình chóp
ABCDS
. có
đ
áy
ABCD
là hình ch
ữ
nh
ậ
t tâm
I
v
ớ
i 32
aAB
=,
aBC
2
=
. Bi
ế
t
chân
đườ
ng cao
H
h
ạ
t
ừ
đỉ
nh
S
xu
ố
ng
đ
áy
ABCD
trùng v
ớ
i trung
đ
i
ể
m
DI
và
SB
h
ợ
p v
ớ
i
đ
áy
ABCD
m
ộ
t góc
0
60 . Tính th
ể
tích kh
ố
i chóp
ABCDS
. và kho
ả
ng cách t
ừ
đế
n )(
SBC
.
Câu 6
(1 điểm
) Cho các s
ố
th
ự
c
y
x
,
v
ớ
i 1
22
=+
yx . Tìm giá tr
ị
nh
ỏ
nh
ấ
t c
ủ
a bi
ể
u th
ứ
c
66
4yxP
+=
PHẦN RIÊNG (3,0 điểm): Thí sinh chỉ được làm một trong hai phần (phần A hoặc phần B)
A. Theo chương trình Chuẩn
Câu 7.a (1,0 điểm)
Trong m
ặ
t ph
ẳ
ng to
ạ
độ
Oxy, cho tam giác ABC v
ớ
i )0;3(A,
đườ
ng cao t
ừ
đỉ
nh
B
có ph
ươ
ng
trình 01
=
+
+
yx , trung tuy
ế
n t
ừ
đỉ
nh C có ph
ươ
ng trình 022
=
−
−
yx . Vi
ế
t ph
ươ
ng trình
đườ
ng tròn ngo
ạ
i ti
ế
p
tam giác ABC.
Câu 8.a (1,0 điểm)
Trong không gian O
xyz
cho )1;1;3(A, )1;0;5(Bvà )1;2;1(
−
−
C. Tìm
đ
i
ể
m M thu
ộ
c m
ặ
t
ph
ẳ
ng (O
xy
) sao cho ABMC
⊥
và di
ệ
n tích tam giác
ABM
b
ằ
ng
2
3.
Câu 9.a (1,0 điểm)
Tìm các s
ố
h
ạ
ng là s
ố
nguyên trong khai tri
ể
n nh
ị
th
ứ
c
(
)
n
3
23 +, bi
ế
t
(
)
2732
3
... PCCCP
n
n
n
n
n
nn
=
,
v
ớ
i
n
là s
ố
t
ự
nhiên.
B. Theo chương trình Nâng cao
Câu 7.b (1,0 điểm)
Trong m
ặ
t ph
ẳ
ng to
ạ
độ
Oxy
, cho
đườ
ng tròn 0364:)(
22
=+−−+
yxyxC
có tâm là
I
và
đườ
ng th
ẳ
ng 0112:
=
−
−
yxd
. Tìm hai
đ
i
ể
m
A
và
B
trên
đườ
ng tròn )(
C
sao cho
AB
song song v
ớ
i
đườ
ng th
ẳ
ng
d
và tam giác
IAB
là tam giác vuông cân.
Câu 8.b (1,0 điểm)
Trong không gian
Oxyz
, cho t
ứ
di
ệ
n
ABCD
, bi
ế
t
(
)
(
)
(
)
1;0;2 , 1;1;0 , 2;1; 2
B C D
− − −
,vect
ơ
OA
cùng ph
ươ
ng v
ớ
i vect
ơ
)1;1;0(=u
và th
ể
tích t
ứ
di
ệ
n
ABCD
b
ằ
ng
6
5. Tìm t
ọ
a
độ
đ
i
ể
m
A
.
Câu 9.b (1,0 điểm)
Gi
ả
i h
ệ
ph
ươ
ng trình
=−
=+
6loglog2
4
2
12
4
log
4
log
yx
yx
xy
-----------------
Hết
-----------------
Thí sinh không được sử dụng tài liệu. Giám thị coi thi không giải thích gì thêm.
H
ọ
và tên thí sinh:………………………………………………; S
ố
báo danh:……………………………
+∞
-∞
-∞+∞
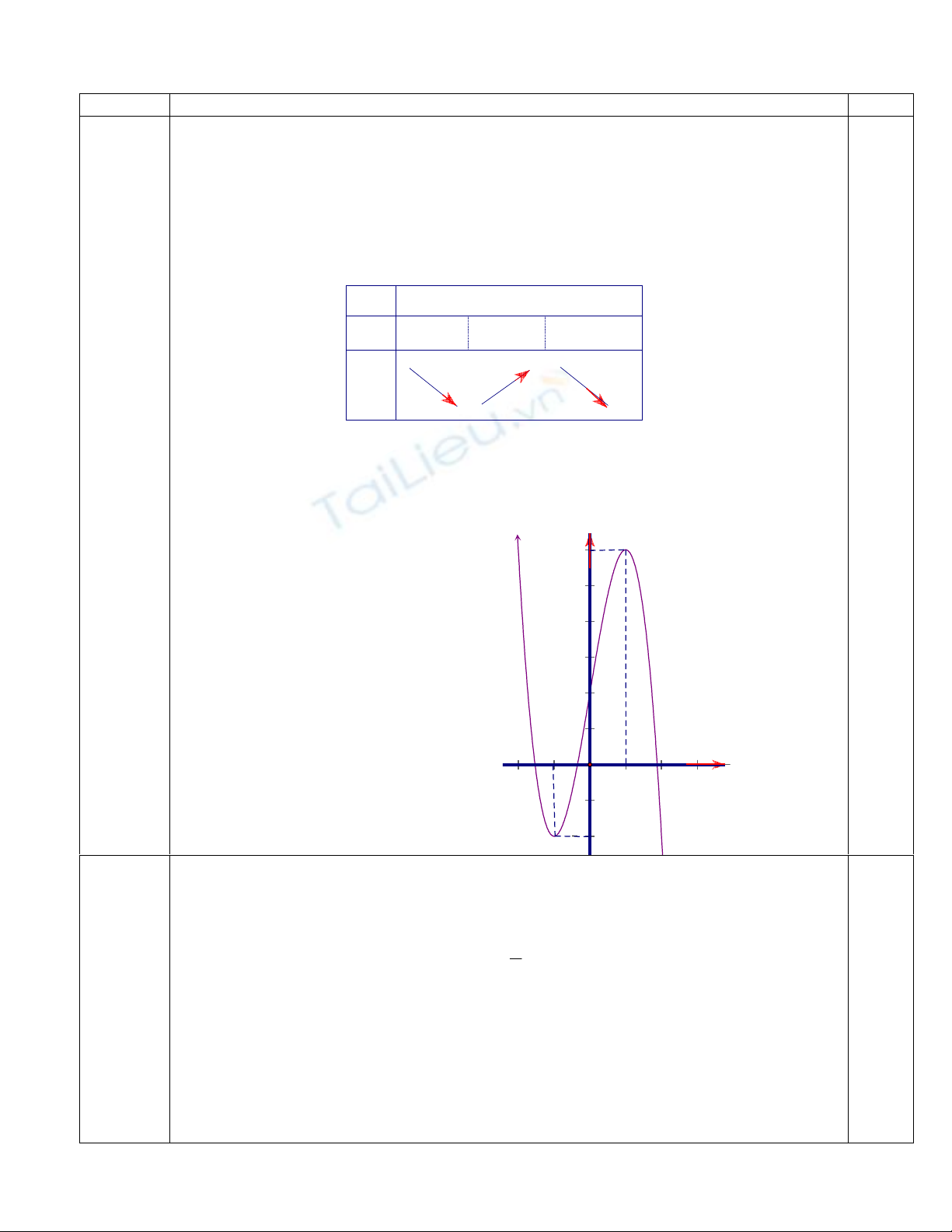
-1 1
6
-
+
-
-2
0
0
y
y
/
x
6
4
2
2
y
0
x
1
-1
ĐÁP ÁN ĐỀ THI THỬ ĐẠI HỌC LẦN 1 KHỐI A-A
1
-B NĂM 2014
Câu Đáp Án Điểm
Câu 1 1.Khảo sát sự biến thiên và vẽ đồ thị hàm số 262
3
++−= xxy
Tập xác định:
R
D
=
Đạo hàm:
66
2/
+−= xy
=
−=
⇔=+−⇔= 1
1
0660
2/
x
x
xy
Giới hạn:
+∞=
−∞→
y
x
lim
;
−∞=
+∞→
y
x
lim
Bảng biến thiên :
Hàm số nghịch biến trên các khoảng )1;(
−
−∞
và );1(
∞
+
, đồng biến trên khoảng
)1,1(
−
. Hàm số đạt cực tiểu 2−=
CT
y
tại 1−=
CT
x
đạt cực đại 6=
CĐ
y
tại 1=
CĐ
x
;
20012
//
=
⇒
=⇔=−=
yxxy
. Điểm uốn là
(
)
)2;0I
Giao điểm với trục hoành: 0
=
y
Giao đi
ểm với trục tung: 20
=
⇒
=
yx
Đồ thị hàm số: nhận điểm I làm tâm đối xứng
0,25
0,25
0,25
0,25
2.
Tìm
m
để đường thẳng
622:
+
−
=
mmxyd
cắt đồ thị (C) tại ba điểm phân
biệt
CBA ,,
sao cho tổng hệ số góc của các tiếp tuyến với (C) tại
CBA ,,
bằng
6
−
.
. 622262
3
+−=++−
mmxxx
0)2)(1(
2
=−++−⇔ mxxx
.Điều kiện cắt tại 3 điểm phân biệt :
4
9
0<≠ m
.G
ọ
i
321
,, xxx là hoành
độ
các
đ
i
ể
m CBA ,,
,
ta có
:
6)()()(
3
/
2
/
1
/
−=++ xfxfxf
6)66()66(0
2
2
2
1
−=+−++−+⇔ xx
32)(
21
2
21
=−+⇔ xxxx
3)2(21
=
−
−
⇔
m
V
ậ
y 1
=
m
0,25
0,25
0.25
0,25
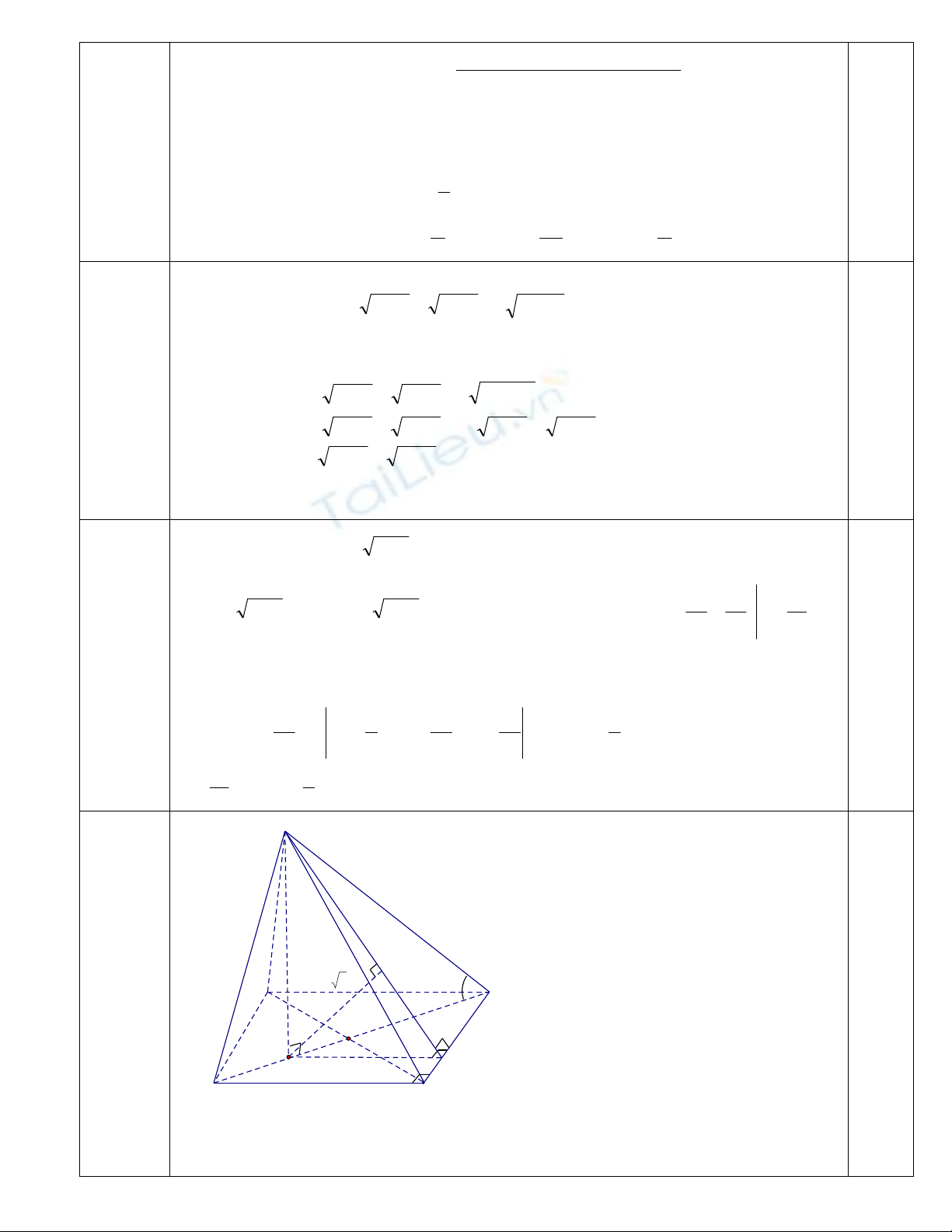
K
M
60°
2a
2a 3
I
H
DC
B
A
S
Câu 2 Giải phương trình
x
xxx
xx
2
432
2
sin
1sin2sin7sin3
cot3sin ++−
=+
(1)
Đ
i
ề
u ki
ệ
n:
π
kxx
≠
⇔
≠
0sin
⇔
xxxxx 222 cot1sin2sin73cot3sin +++−=+
04sin10sin2sin4
23
=+−+⇔
xxx
.Gi
ả
i ph
ươ
ng trình ta
đượ
c
2
1
sin =
x
,1sin
=
x
,2sin
−
=
x
(L)
.V
ậ
y ph
ươ
ng trình có nghi
ệ
m
π
π
2
6
kx
+= ,
π
π
2
6
5
kx
+= ,
π
π
2
2
kx
+=
0,25
0,25
0,25
0,25
Câu 3
Giải hệ phương trình
−=−−−++
=++−
12216244
02)2(
222
xyxx
xyxy
.Điều kiện: 16,4
≥
≥
yx
.Giải phương trình (2) theo ẩn
y
ta được
2
),(2
xyLy
==
Thay vào (1) ta có
12216244
2
−=−−−++ xxxx
(
)
(
)
0124444
2
=−−++−−++⇔ xxxx
444 =−++⇔ xx
Gi
ả
i ph
ươ
ng trình ta
đượ
c 5
=
x
V
ậ
y h
ệ
đ
ã cho có nghi
ệ
m )25,5(
0,25
0,25
0,25
0,25
Câu 4 Tính tích phân
( )
∫
+−=
2
1
ln1 dxxxxI
∫
−=
2
1
1
1dxxxI .
Đặ
t 1−= xu , ta
đượ
c 15
16
35
22.)1(
1
0
35
1
0
2
1
=
+=+=
∫
uu
uduuuI
∫
=
2
1
2
ln xdxxI
Đặ
t xdxdvxu
=
=
,ln , ta
đượ
c
∫
−=
2
1
2
1
2
2
2
ln
2dx
x
x
x
I
=
4
3
2ln2
4
ln
2
2
1
22
−=−= x
x
x
4
3
2ln2
15
16 −+=I
0,25
0,25
0,25
0,25
Câu 5
Tính thể tích của khối chóp S.ABCD
Xác
đị
nh
đ
úng góc
0
60=
∧
SBH
0,25
+
4
9
1
0
t
f
/
(t)
f(t)
_
0
1
4
2
3
.
3
.
1233.2.32
3
1
..
3
1
.
3
1aaaaBCSHABSHSV
ABCDABCDS
====
Khoảng cách
(
)
)(, SBCHd
.Xác
đị
nh
(
)
HKSBCHd =)(,
.
222222
27
5
27
4
27
1111
a
a
a
HM
SH
HK
=+=+=
( )
15
5
3
)(, aHKSBCHd ==
0,25
0,25
0,25
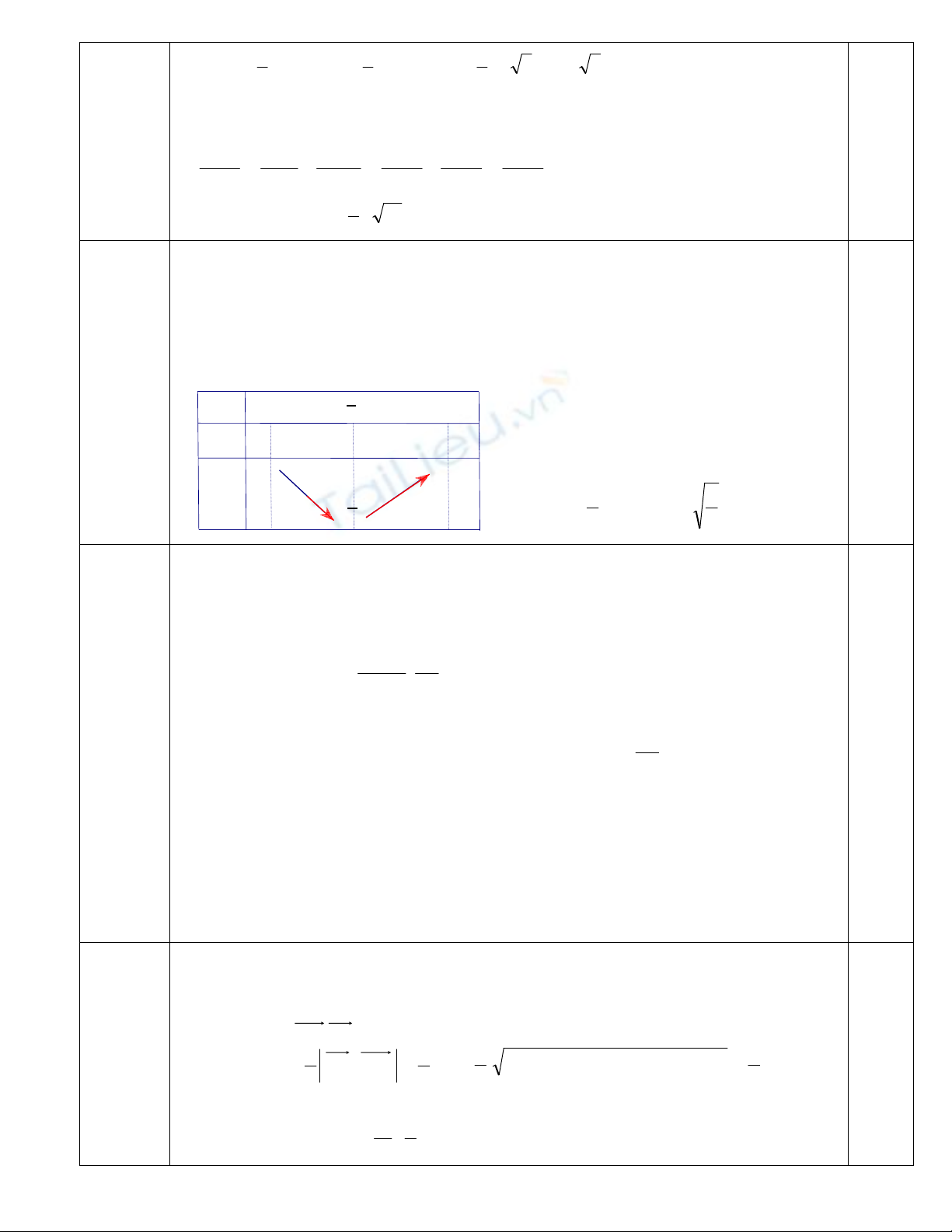
Câu 6 Tìm giá trị nhỏ nhất của biểu thức
.Ta có
2222
11 xyyx −=
⇒
=+
32666
)1(44 xxyxP −+=+=
.
Đặ
t
2
xt = v
ớ
i 10
≤
≤
t
.Xét hàm s
ố
33
)1(4)( tttf −+= .
22/
)1(123)( tttf −−=
9
4
=PGTNN khi
3
2
±=x
0,25
0,25
0,25
0,25
Câu 7a Viết phương trình đường tròn ngoại tiếp tam giác ABC.
• (AC) qua
đ
i
ể
m A( 3;0) và vuông góc (BH)
⇒
(AC): 03
=
−
−
yx .
⇒
∩
=
)()( CMACC t
ọ
a
độ
C là nghi
ệ
m h
ệ
: )4;1(
022
03 −−
⇒
=−−
=−− C
yx
yx .
• G
ọ
i
);(
BB
yxB
⇒
)
2
;
2
3
(
BB
yx
M+ ( M là trung
đ
i
ể
m AB)
Ta có B thu
ộ
c )(BH và M thu
ộ
c )(CM nên ta có: )0;1(
02
2
3
01
−⇒
=−−+
=++
B
y
x
yx
B
B
BB
• G
ọ
i ph
ươ
ng trình
đườ
ng tròn qua A, B, C có d
ạ
ng:
022
22
=++++ cbyaxyx . Thay t
ọ
a
độ
ba
đ
i
ể
m A, B, C vào pt
đườ
ng tròn ta có
−=
=
−=
⇔
−=+−−
−=+−
−=+
3
2
1
1782
12
96
c
b
a
cba
ca
ca
Ph
ươ
ng trình
đườ
ng tròn qua A, B, C là: 0342:)(
22
=−+−+ yxyxC .
0,25
0,25
0,25
0,25
Câu 8a Tìm điểm M thuộc mặt phẳng
(O
xy
)
.
(
)
)0;;( yxMOxyM ⇒∈
.Theo gi
ả
thuy
ế
t ta có
[ ]
==
=
2
3
,
2
1
0.
AMABS
ABCM
ABM
[ ]
=−+−+−
=−−−
⇔
2
3
)3()1(2)10(5.
2
1
0)2()1(2
2
2xy
yx
.Gi
ả
i h
ệ
t
ươ
ng
ứ
ng
.V
ậ
y )0;2;3(M và
0;
5
2
;
5
11
M
0,25
0,25
0,25
0,25
Câu 9a Tìm các số hạng là số nguyên trong khai triển nhị thức
(
)
n
3
23
+
, biết
(
)
2732
3
... PCCCP
n
n
n
n
n
nn
=
, với
n
là số tự nhiên.
.Gi
ả
i ph
ươ
ng trình
(
)
2732
3
...
PCCCP
n
n
n
n
n
nn
=
9
=
⇒
n
.S
ố
h
ạ
ng t
ổ
ng quát
3
2
9
9
2.3
k
k
k
C
−
.S
ố
h
ạ
ng là s
ố
nguyên khi
2
9k
−
và
3
k là s
ố
nguyên 3
=
⇒
k và 9
=
k
.V
ậ
y có 2 s
ố
h
ạ
ng là : 45362.3
133
9
=C và 82.
39
9
=C
0,25
0,25
0,25
0,25
Câu 7b Tìm hai điểm
A
và
B
trên đường tròn
)(C
sao cho
AB
song song với đường thẳng
d
và tam giác
IAB
là tam giác vuông cân.
.dAB //)( 02:)(
=
+
−
⇒
CyxAB
. Tam giác
IAB
là vuông cân
2
2
),( R
ABId
=
⇒
2
2.10
5
3.22
=
+−
⇔
C
9
=
⇒
C và 1
−
=
C
1
−
=
C: Gi
ả
i h
ệ
=−−
=+−−+
012
0364
22
yx
yxyx
)2;5(,)0;1( BA
⇒
9
=
C: Gi
ả
i h
ệ
=+−
=+−−+
092
0364
22
yx
yxyx
)6;3(,)4;1( BA
−
⇒
0,25
0,25
0,25
0,25
Câu 8b Tìm tọa độ điểm
A
.
T
ừ
gi
ả
thi
ế
t có
. (0; ; )
OA t u t t
= =
);;0( ttA
⇒
. Suy ra
, 9 4.
BC BD BA t
= − +
Ta có
ABCD
V
=
1 5 1
, 9 4
6 6 6
BC BD BA t
⇔ = − +
1
1;
9
t t
⇔ = = −
.
V
ớ
i
1 (0;1;1)
t A
=
⇒
.
V
ớ
i 1
0
9
t
= − <
,
V
ậ
y có 2
đ
i
ể
m
A
th
ỏ
a là )1;1;0(A và )
9
1
;
9
1
;0(
−−
A
0,25
0,25
0,25
0,25
Câu 9b
Giải hệ phương trình
=−
=+
6loglog2
4
2
12
loglog
44
yx
yx
xy
Đ
i
ề
u ki
ệ
n 0,
>
yx
Khi
đ
ó, ta có h
ệ
đ
ã cho t
ươ
ng
đươ
ng v
ớ
i
=−
=
6loglog2
42
2
12
log
4
yx
x
y
=+
=
⇔3loglog
2log.log
22
22
yx
yx
=
=
⇔2log
1log
2
2
y
x
ho
ặ
c
=
=
⇔1log
2log
2
2
y
x
V
ậ
y nghi
ệ
m c
ủ
a h
ệ
ph
ươ
ng trình
đ
ã cho là: )4;2( và )2;4(
0,25
0,25
0,25
0,25