Mã đề 101 Trang 1/13
SỞ GIÁO DỤC VÀ ĐÀO TẠO
THANH HOÁ
TRƯỜNG THPT HÀ TRUNG
KỲ THI THỬ TỐT NGHIỆP THPT LẦN I
NĂM HỌC 2024 – 2025
Môn thi: TOÁN
Thời gian làm bài: 90 phút, không kể thời gian phát đề.
Kỳ thi ngày 11 tháng 1 năm 2025
ĐỀ CHÍNH THỨC
Mã đề thi 101
(Đề thi có 04 trang )
Họ và tên thí sinh:……………………………… Số báo danh:……………………..…
PHẦN I. [3 điểm] Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1. Nghiệm của phương trình 1
3 27
x
là
A.
5x
. B.
3x
. C.
4x
. D.
2x
.
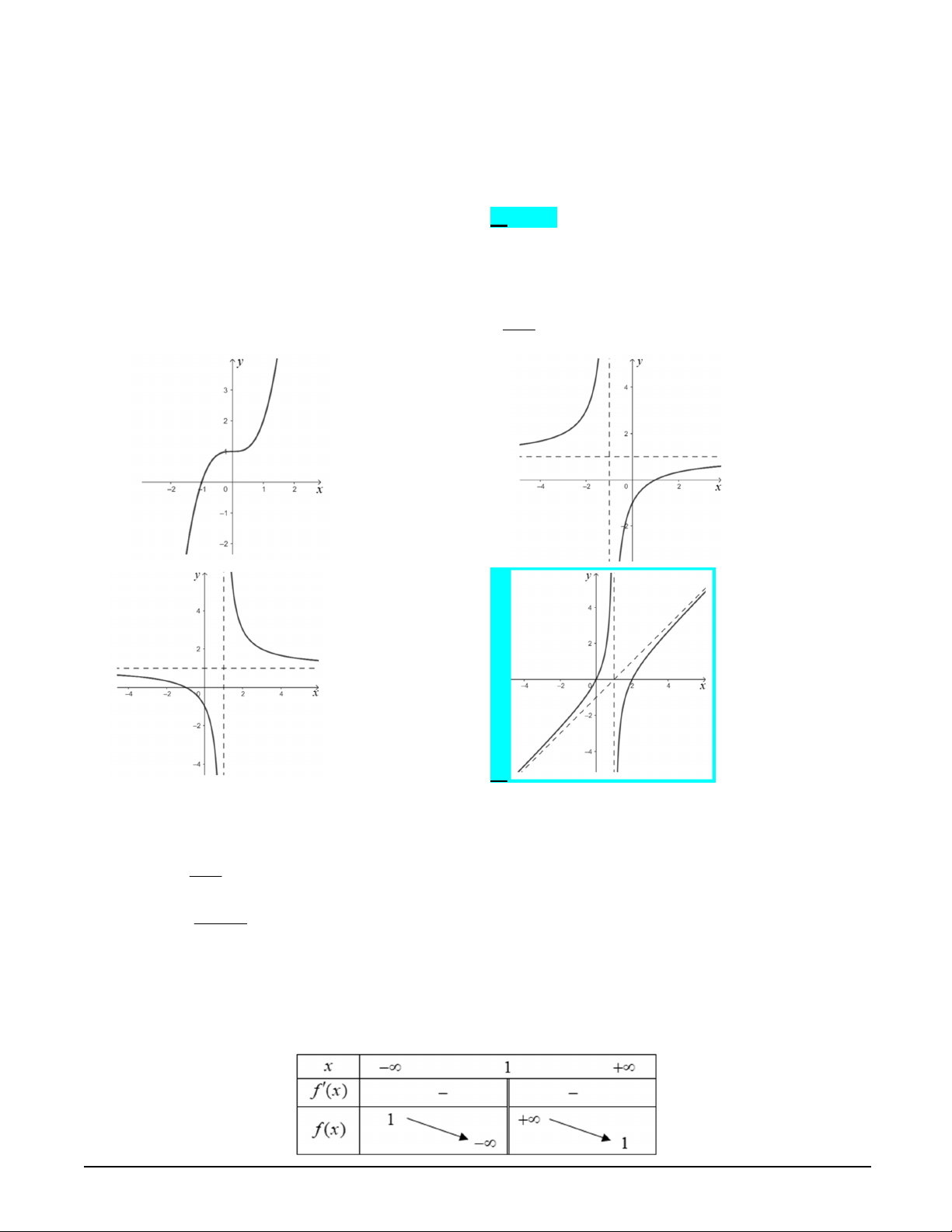
Câu 2. Đường cong nào dưới đây là đồ thị của hàm số
1
1
x
yx
A. . B. .
C. . D. .
Câu 3. Trong không gian với hệ trục tọa độ
Oxyz
, cho ba vecto
1;2;3 ; 2;2; 1 ; 4;0; 4
a b c
.
Tọa độ của vecto
2d a b c
là
A.
7;0; 4d
. B.
7;0;4d
. C.
7;0; 4d
. D.
7;0;4d
.
Câu 4. Từ một hộp chứa
11
quả cầu màu đỏ và
4
quả cầu màu xanh, lấy ngẫu nhiên đồng thời 3 quả cầu. Xác
suất để lấy được
3
quả cầu màu xanh
A.
33
91
. B.
4
455
. C.
4
165
. D.
24
455
.
Câu 5. Trong không gian
Oxyz
, cho hai điểm
3; 2;3A
và
1;2;5B
. Tìm tọa độ trung điểm
I
của đoạn
thẳng
AB
.
A.
1; 0; 4I
. B.
2; 2; 1I
. C.
2; 2; 1I
. D.
2; 0; 8I
.
Câu 6. Cho hàm số
y f x
có bảng xét dấu đạo hàm như sau
Mã đề 101 Trang 2/13
Mệnh đề nào dưới đây đúng?
A. Hàm số đồng biến trên khoảng
2;0
B. Hàm số nghịch biến trên khoảng
; 2
C. Hàm số đồng biến trên khoảng
;0
D. Hàm số nghịch biến trên khoảng
0;2
Câu 7. Tìm tập xác định của hàm số
3
log 3y x
.
A.
3;D
. B.
3;D
. C.
0;D
. D.
\ 3D
.
Câu 8. Cho hàm số
y f x
xác định trên
\ 0
liên tục trên mỗi khoảng xác định và có bảng biến thiên sau.
Hỏi đồ thị hàm số đã cho có bao nhiêu đường tiệm cận?
A. 2. B. 4. C. 5. D. 3.
Câu 9. Bảng số liệu bên dưới biểu diễn số liệu ghép nhóm về nhiệt độ không khí trung bình các tháng
trong năm
2021
tại Hà Nội (đơn vị: độ
C
) (Nguồn: Niên giám thống kê
2021
, NXB Thống kê,
2022
).
Độ lệch chuẩn (làm tròn đến chữ số hàng phần trăm) của mẫu số liệu đã cho bằng
A.
4,55
. B.
4,56
. C.
4,6
. D.
4,5
.
Câu 10. Cho hình chóp
.S ABC
có đáy
ABC
là tam giác đều cạnh
a
. Biết
SA ABC
và
3SA a
. Tính thể
tích khối chóp
.S ABC
.
A.
3
2
a
. B.
4
a
. C.
3
4
a
. D.
3
3
4
a
.
Câu 11. Dãy số nào sau đây không phải là cấp số nhân?
A.
1; 2;4; 8;16
. B.
1; 2; 4; 8; 16
. C.
1; 1; 1; 1; 1
. D.
1; 3; 9; 27; 54
.
Câu 12. Cho hình hộp
.ABCD A B C D
, khi đó tổng của các vecto
'AA AC
là
y'
+
∞
0
3
4
3
0
+
3
0+
∞
∞
y
x
Mã đề 101 Trang 3/13
A.
'AB
. B.
' 'A C

. C.
'AD
. D.
'AC
.
PHẦN II. [4 điểm] Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng
hoặc sai.
Câu 1. Trong hệ trục tọa độ
Oxyz
cho 3 điểm
5; 2;0 , 4;5; 2
A B
và
0;3;2
C
. Điểm
M
di chuyển
trên trục
Ox
và điểm
N
thỏa mãn đẳng thức
2 0NA NB NC
a) Hoành độ và tung độ của điểm
N
bằng nhau.
b)
1; 7;2AB
.
c) Giá trị nhỏ nhất của biểu thức
2 3Q MA MB MC MB MC

là
6 35
.
d) Trọng tâm tam giác
ABC
là điểm
3;2;0G
.
Câu 2. Cho hai hàm số
sinf x x x
và
2
sin 2 3g x x x m m
. Gọi
S
là tập các giá trị của
m
để
giá trị lớn nhất của hàm
y g x
trên đoạn
0;
bằng
4
.
a) Tập
S
có hai phân tử.
b) Nghiệm của phương trình
' 0f x
là
2x k k
.
c)
1
2 2
f
.
d) Hàm số
y f x
đồng biến trên tập xác định.
Câu 3. Cho hàm số
3 2
2
x
yx
có đồ thị là
C
. Hai điểm
,A B
thuộc hai nhánh của đồ thị
C
.
a) Giá trị nhỏ nhất của hàm số
3 2
2
x
yx
trên đoạn
2;5
là
2
.
b) Khi độ dài đoạn
AB
ngắn nhất thì
. 29OAOB
.
c) Hàm số đồng biến trên
\ 2
.
d) Đường thẳng
3y
là tiệm cận ngang của đồ thị
C
.
Câu 4. Có hai hộp chứa các tấm thẻ. Hộp I chứa 5 tấm thẻ màu vàng được đánh số từ 1 đến 5, hộp II chứa
7 tấm thẻ màu đỏ được đánh số từ 1 đến 7. Lấy ngẫu nhiên từ mỗi hộp một tấm thẻ.
a) Sau khi 2 tấm thẻ được lấy ra ta ghép chúng với nhau để được một số có hai chữ số (chữ số hàng chục là
thẻ màu vàng và chữ số hàng đơn vị là thẻ màu đỏ). Xác suất để thu được số chia hết cho 3 bằng
14
35
.
b) Xác suất chọn được hai tấm thẻ có số giống nhau bằng
1
5
.
c) Số phần tử của không gian mẫu bằng 35.
d) Xác suất để tích các số trên hai tấm thẻ lấy được là một số chẵn bằng
6
35
.
PHẦN III. [3 điểm] Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1. An và Bình thi đấu với nhau một trận bóng bàn, người nào thắng trước 3 séc sẽ giành chiến thắng
chung cuộc. Xác suất An thắng mỗi séc là (không có hòa). Tính xác suất An thắng chung cuộc. ( Kết quả
làm tròn đến hàng phần trăm).
0, 4
Mã đề 101 Trang 4/13
Câu 2. Cho tứ diện
ABCD
có độ dài các cạnh
3, 4, 6AB AC AD
và các góc
60BAC BAD
,
90
CAD
. Tính khoảng cách giữa hai đường thẳng
AB
và
CD
. (kết quả làm tròn đến phần trăm)
Câu 3. Ba chiếc máy bay không người lái cùng bay lên tại một địa điểm. Sau một thời gian bay, chiếc máy bay
thứ nhất cách điểm xuất phát về phía Đông
60 km
và về phía Nam
40 km
, đồng thời cách mặt đất
2km
.
Chiếc máy bay thứ hai cách điểm xuất phát về phía Bắc
80
km
và về phía Tây
50
km
, đồng thời cách mặt
đất
4km
. Chiếc máy bay thứ ba nằm chính giữa của chiếc máy bay thứ nhất và thứ hai, đồng thời ba chiếc
máy bay này thẳng hàng. Xác định khoảng cách của chiếc máy bay thứ ba với vị trí tại điểm xuất phát của nó.
Câu 4. Độ giảm huyết áp của một bệnh nhân được cho bởi công thức , trong đó là
liều lượng thuốc được tiêm cho bệnh nhân ( được tính bằng miligam). Tính liều lượng thuốc cần tiêm (đơn vị
miligam) cho bệnh nhân để huyết áp giảm nhiều nhất.
Câu 5. Có bao nhiêu giá trị nguyên của tham số m thuộc
2025;2025
để hàm số
2
2
log 2
log 1
m x
yx m
nghịch
biến trên
4;
.
Câu 6. Một người đưa thư xuất phát từ bưu điện ở vị trí A, các điểm cần phát thư nằm dọc các con đường cần đi
qua. Biết rằng người này phải đi trên mỗi con đường ít nhất một lần (để phát được thư cho tất cả các điểm cần
phát nằm dọc theo con đường đó) và cuối cùng quay lại điểm xuất phát. Độ dài các con đường như hình vẽ (đơn
vị độ dài). Hỏi tổng quãng đường người đưa thư có thể đi ngắn nhất có thể là bao nhiêu ?
------ HẾT ------
2
0,035 15
G x x x
x
x
Mã đề 101 Trang 5/13
HƯỚNG DẪN GIẢI
PHẦN I. [3 điểm] Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1. Nghiệm của phương trình 1
3 27
x
là
A.
5x
. B.
3x
. C.
4x
. D.
2x
.
Lời giải
Ta có 1
3 27 1 3 4.
x
x x
Vậy
4x
là nghiệm của phương trình.
Câu 2. Đường cong nào dưới đây là đồ thị của hàm số
1
1
x
yx
A. . B. .
C. . D. .
Lời giải
Chọn D
2
1; \ 1
1
2
' 0,
1
x
y D
x
y x D
x
lim 1
x
y

nên đồ thị có tiệm cân ngang là đường thẳng
1y
.
1 1
lim ; lim
x x
y y
 
nên đồ thị có tiệm cân đứng là đường thẳng
1x
.
Bảng biến thiên: