200 Giaùo Trình Vaät Lyù Ñaïi Cöông – Taäp I: Cô – Nhieät - Ñieän
(9.34)
→→
=α==Φ SdDcosDdSdS.Dd nD
(9.35)
∫∫ →→
=Φ=Φ
SS
DD SdDd
§9.4 ĐỊNH LÍ OSTROGRADSKY – GAUSS (O – G)
1 – Thiết lập định lý:
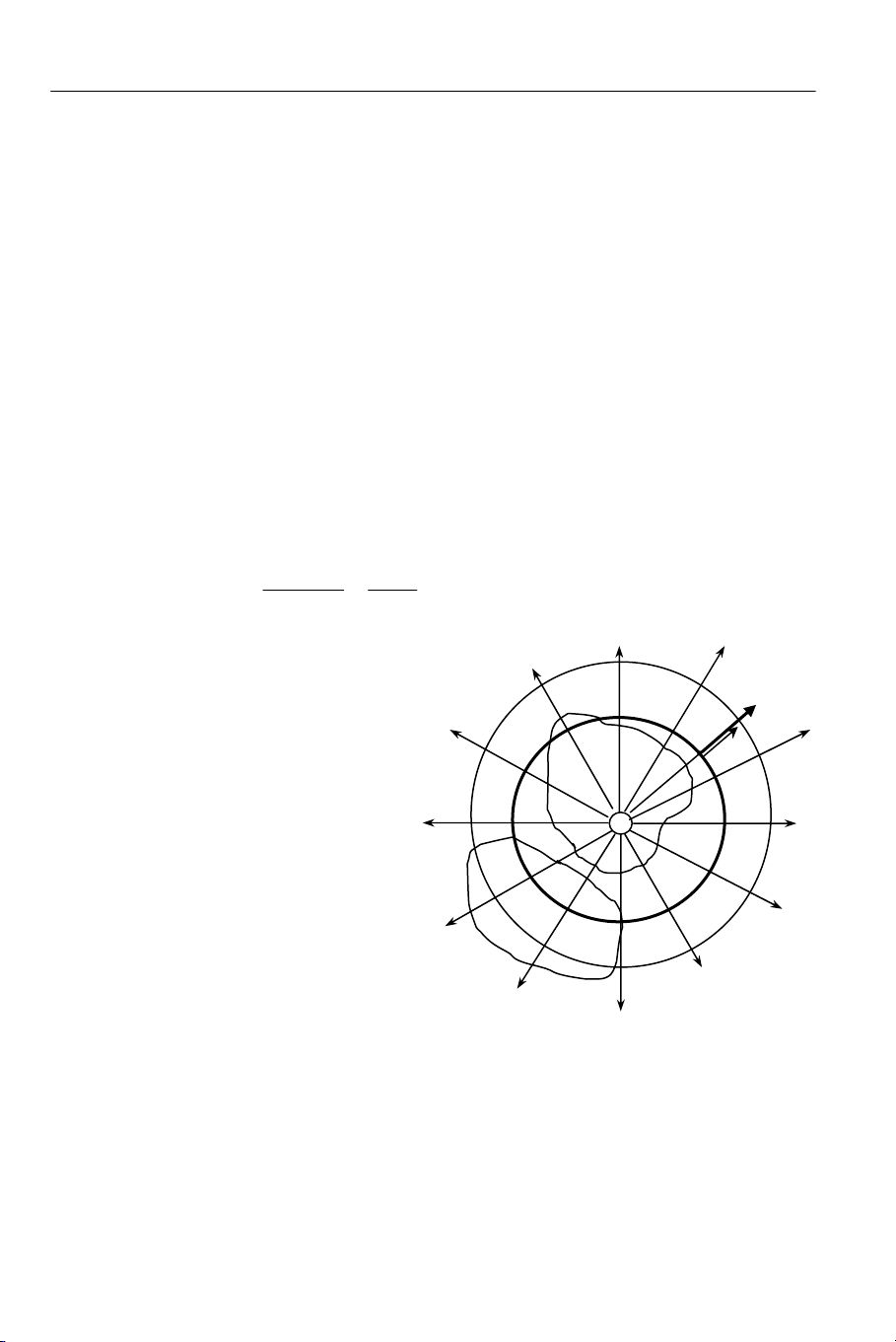
Xét điện tích điểm Q > 0. Bao quanh Q một mặt cầu (S), tâm là Q, bán kính r.
Thông lượng điện cảm gởi qua mặt cầu này là: DD
(S) (S)
dDdScoΦ= Φ= α
∫∫
s
v
v. Do tính
đối xứng cầu nên D = const tại mọi điểm trên mặt cầu và α = 0 (vì pháp tuyến của mặt
(S) luôn trùng với đường cảm ứng điện, xem hình 9.11). Do đó, thông lượng điện cảm
gởi qua mặt kín (S) là: D
(S) (S)
DdS D dS DSΦ= = =
∫∫
v
v
Mà D = εεoE = εεo.22
or4
Q
r4
Q
π
=
πεε ; S = 4πr2
Suy ra: Φ (9.36) Q
D=
M
r
→
D
→
n
+
S3
S2
S1
S
Nhận xét:
- Thông lượng điện cảm D
Φ
gởi qua
mặt cầu (S) không phụ thuộc vào
bán kính r của mặt cầu. Suy ra đối
với bất kì mặt cầu nào đồng tâm với
(S), ví dụ (S1), ta cũng có (9.36).
Như vậy, trong khoảng không gian
giữa hai mặt cầu (S) và (S1), nơi
không có điện tích, các đường cảm
ứng điện là liên tục, không bị mất
đi và cũng không thêm ra. Do đó,
nếu xét mặt kín (S2) bất kì bao
quanh Q thì ta cũng có (9.36).
- Nếu có mặt kín (S3) không bao
quanh Q thì có bao nhiêu đường cảm ứng điện đi vào (S3) thì cũng có bấy nhiêu
đường cảm ứng điện đi ra khỏi (S3), nên thông lượng điện cảm gởi qua (S3) bằng
không.
Hình 9.11: Định lí O – G
Tóm lại, thông lượng điện cảm gởi qua một mặt kín không phụ thuộc vị trí điện tích
bên trong nó. Kết quả (9.36) cũng đúng cho cả trường hợp bên trong mặt kín chứa
nhiều điện tích, phân bố bất kì, khi đó Q là tổng đại số các điện tích bên trong mặt kín.
Simpo PDF Merge and Split Unregistered Version - http://www.simpopdf.com

Chöông 9: ĐIỆN TRƯỜNG TĨNH 201
2 – Phát biểu định lí O – G:
Thông lượng điện cảm gởi qua một mặt kín bất kỳ bằng tổng đại số các điện
tích chứa trong mặt kín đó.
(9.37)
D
S
Qhay DdS Q
trong (S)
→→
Φ= =
∑∑
∫v
Trong chân không thì = ε
→
Do
→
E, nên ta có:
o
(S) trong
ε
=
∑
∫→→ Q
Sd.E
S
(9.38)
và định lý O – G còn được phát biểu là: điện thông gởi qua một mặt kín bất kì bằng
tổng đại số các điện tích bên trong mặt kín đó chia cho hằng số điện
ε
o.
3 – Dạng vi phân của định lí O – G:
(9.37) được gọi là dạng tích phân của định lí O – G. Trong trường hợp điện
tích phân bố liên tục, ta có thể biểu diễn định lí O – G dưới dạng vi phân.
Muốn vậy, ta áp dụng một định lí trong giải tích, cũng có tên là định lí O – G,
biến một tích phân mặt thành tích phân theo thể tích. Theo đó, vế trái của (9.37) được
viết là:
S
D.dS divD.d
→→ →
τ
=
τ
∫∫v (9.39)
Trong đó, là thể tích của không gian giới hạn bởi mặt kín (S) và d
τ
τ
là yếu tố thể
tích; div là một toán tử vi phân tác động lên một vectơ và trả về một vô hướng, trong
hệ tọa độ Descartes, ta có: y
x
D
DD
div D xyz
→
z
∂
∂
∂
=++
∂
∂∂
(9.40)
Vì điện tích phân bố liên tục nên vế phải của (9.37) trở thành:
trong(S)
Q
τ
d
=
ρτ
∑
∫
(9.41)
Thay (9.39) và (9.41) vào (9.37), ta được: div D.d d
→
ττ
τ
=ρτ
∫
∫.
Suy ra : (div D )d 0
→
τ
−
ρτ=
∫ (9.42)
Vì (9.37) đúng với mặt kín (S) bất kì, nên (9.42) đúng với thể tích
τ
bất kì. Điều này
chứng tỏ : div D 0
→
−
ρ= hay div D
→
=
ρ (9.43)
Trong môi trường đẳng hướng, ta có:
0
div E
→
ρ
=
ε
ε (9.44)
Simpo PDF Merge and Split Unregistered Version - http://www.simpopdf.com
202 Giaùo Trình Vaät Lyù Ñaïi Cöông – Taäp I: Cô – Nhieät - Ñieän
(9.43), (9.44) là dạng vi phân của định lí O – G. Nó diễn tả mối quan hệ giữa vectơ
điện cảm , vectơ cường độ điện trường với mật độ điện tích ρ ở từng điểm trong
điện trường.
D
→
E
→
4 – Vận dụng định lý O – G để tính cường độ điện trường:
Định lý O – G thường được sử dụng để tính cường độ điện trường của một số
hệ điện tích phân bố đối xứng không gian, cụ thể là đối xứng cầu, đối xứng trụ và đối
xứng phẳng. Các bước thực hiện:
• Bước 1: Chọn mặt kín S (gọi là mặt Gauss) đi qua điểm khảo sát, sao cho
việc tính thông lượng điện cảm D
Φ
(hoặc điện thông E
Φ
) được đơn giản
nhất. Muốn vậy, phải căn cứ vào dạng đối xứng của hệ đường sức để suy
ra qũi tích những điểm có cùng độ lớn của vectơ điện cảm (hoặc vectơ
cường độ điện trường) với điểm khảo sát.
• Bước 2: Tính thông lượng điện cảm D
Φ
(hoặc điện thông E
Φ
) gởi qua
mặt Gauss và tính tổng điện tích chứa trong (S).
• Bước 3: Thay vào (9.37) hoặc (9.38) suy ra đại lượng cần tính.
Ví dụ 9.4: Xác định cường độ điện trường gây bởi khối cầu tâm O, bán kính a, tích
điện đều với mật độ điện tích khối
ρ
> 0 tại những điểm bên trong và bên ngoài khối
cầu.
Giải
Do tính đối xứng cầu nên hệ đường sức là mhững đường thẳng xuyên tâm và hướng
xa tâm O, vì ρ > 0. Suy ra, các điểm có D = const nằm trên mặt cầu tâm O.
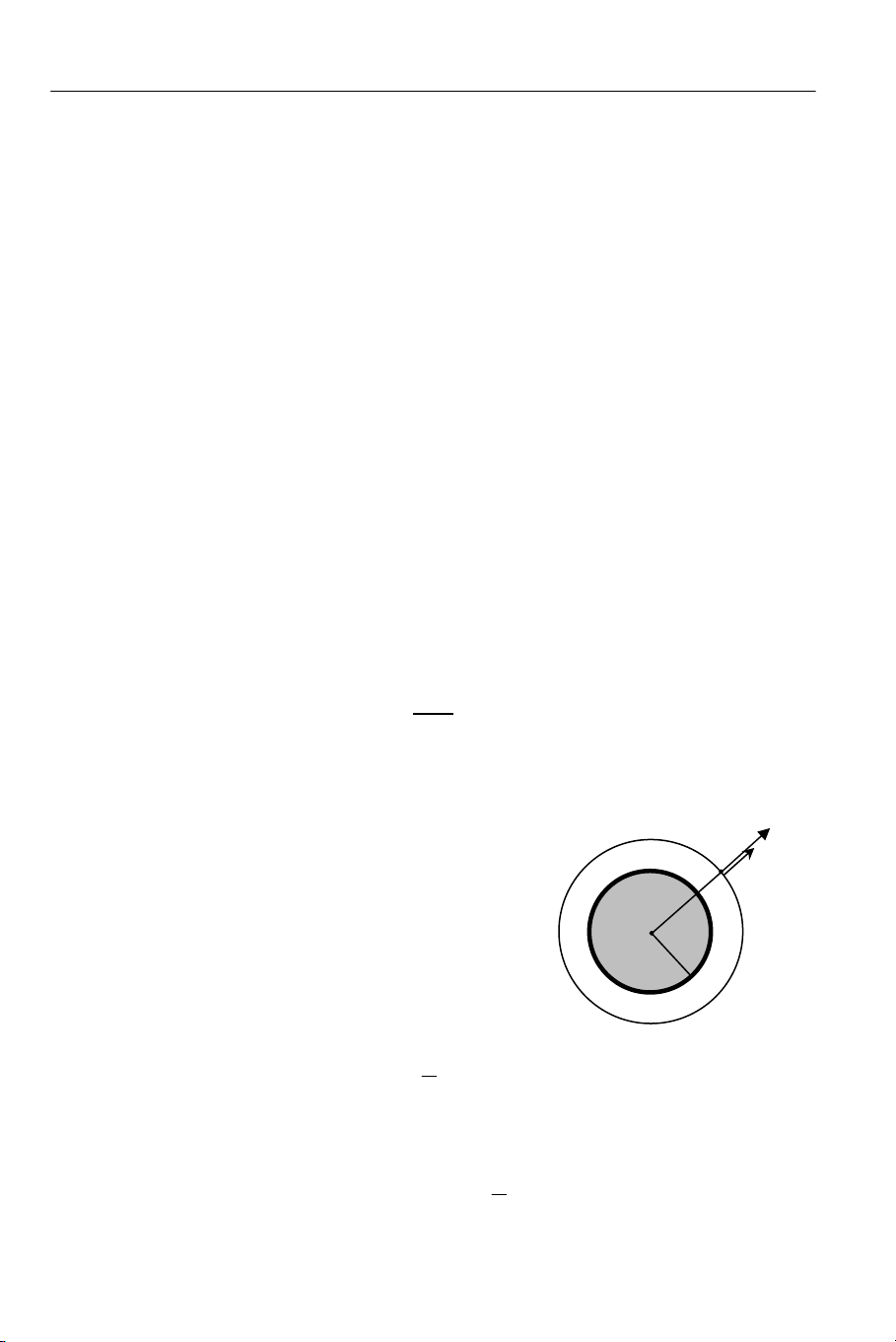
a) Xét điểm M nằm ngoài khối cầu:
Bước 1: Chọn mặt (S) là mặt cầu tâm O, đi qua M.
Bước 2: Thông lượng điện cảm gởi qua mặt Gauss
(S):
DG
→
E
auss
a
r
M
O
→
n
SS S
DdS D.dS D dS DS
→→
Φ= = = =
∫∫ ∫vv v
Với D = εεoE ; SGauss =4πr2
2
D0
E.4 r⇒Φ =εε π
Tổng điện tích chứa trong mặt Gauss:
Q = 3
a.
3
4
..d πρ=τρ=τρ
∫
Q=
τ
(S) trong
∑ Hình 9.12: CĐĐT bên
ngoài khối cầu
với là thể tích khối cầu τ
Bước 3: Vì nên εε
∑
=Φ (S) trong
Q
Do.E.4πr2 = 3
a
3
4ρπ
Simpo PDF Merge and Split Unregistered Version - http://www.simpopdf.com
Chöông 9: ĐIỆN TRƯỜNG TĨNH 203
⇒ 22
o
3
r
kQ
r3
a
Eε
=
εε
ρ
= hay ở dạng vectơ:
r
r
.
r
kQ
E2
→
→
ε
= (9.45)
Mở rộng: đối với mặt cầu tích điện đều với điện tích tổng cộng Q thì (9.45) vẫn đúng.
Vậy, một khối cầu hoặc một mặt cầu tích điện đều với điện tích Q thì điện trường mà
nó gây ra xung quanh nó giống như điện trường gây bởi điện tích điểm Q đặt tại tâm
khối cầu hoặc mặt cầu.
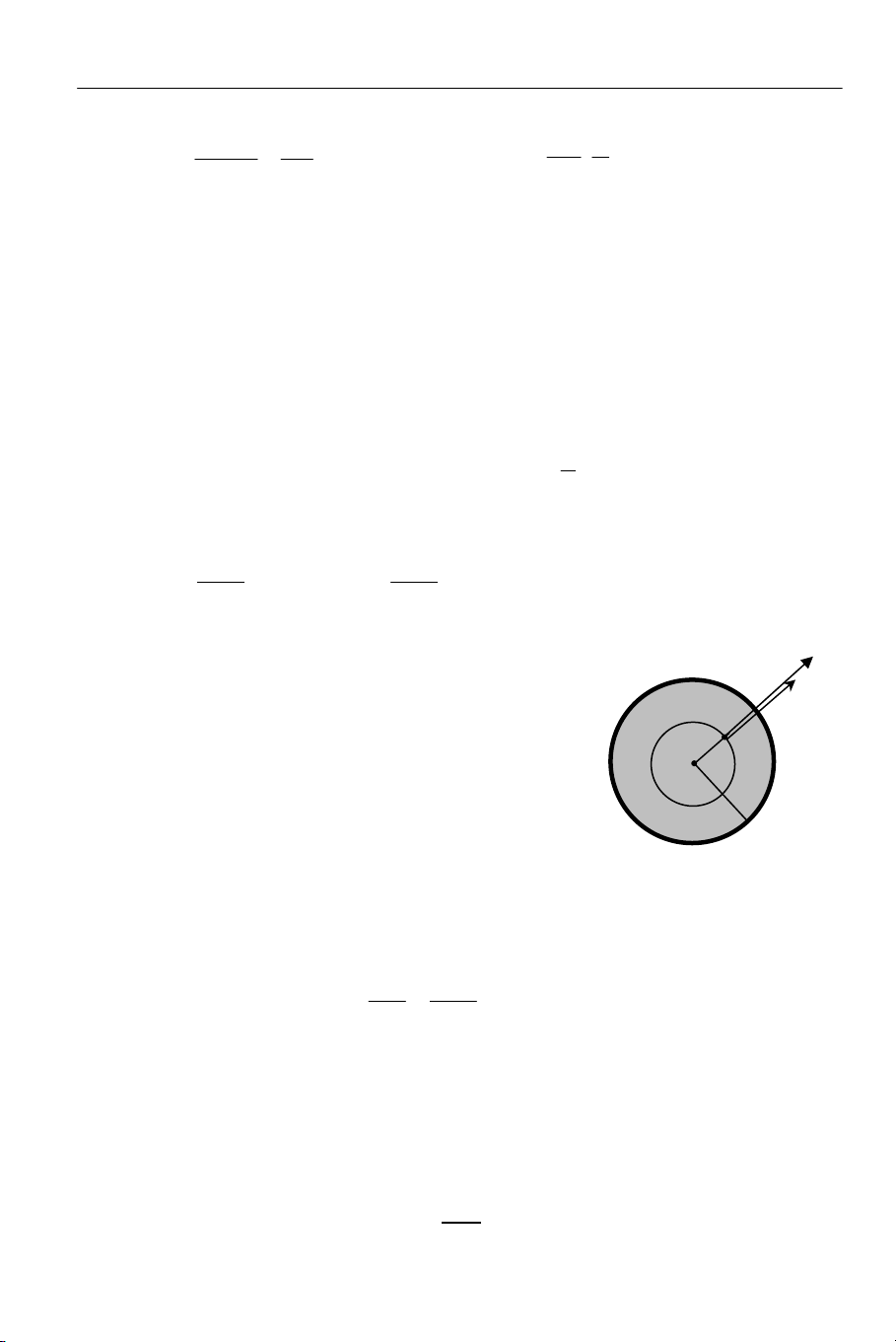
b) Xét điểm M bên trong khôi cầu:
Tương tự ta cũng chọn mặt kín Gauss là mặt cầu, tâm O, bán kính r (r < a).
Điện thông gởi qua mặt Gauss là:
2
oD r.E4πεε=Φ
Tổng điện tích chứa trong mặt Gauss là Q = 3
r
3
4
.. πρ=τρ ; với
τ
là thể tích không
gian chứa trong mặt Gauss.
Suy ra:
o
3
r
Eεε
ρ
= hay
o
3
r
Eεε
ρ
=
→
→
trong (9.46)
O
M
r
a
→
E
→
n
Mở rộng: Nếu điện tích chỉ phân bố trên mặt cầu (ví dụ
vỏ cầu hoặc quả cầu kim loại) thì ρ = 0 nên trong lòng
quả cầu E = 0, nghĩa là không có điện trường.
Nhận xét: Cường độ điện trường bên trong và bên ngoài
khối cầu biến thiên theo hai qui luật khác nhau:
• Bên trong khối cầu, cường độ điện trường tỉ lệ bậc
nhất với khoảng cách r.
• Bên ngoài khối cầu, cường độ điện trường tỉ lệ
nghịch với r2. Hình 9.13: CĐĐT bên
trong khối cầu
• Ngay tại mặt cầu, cường độ điện trường đạt giá trị
lớn nhất:
o
2
max 3
a
a
kQ
Eεε
ρ
=
ε
= (9.47)
• Các kết quả (9.45) và (9.46) vẫn đúng trong trường hợp quả cầu tích điện âm,
khi đó vectơ cường độ điện trường hướng vào tâm O.
Ví dụ 9.5: Xác định phân bố cường độ điện trường gây bởi mặt phẳng rộng vô hạn,
tích điện đều với mật độ điện tích mặt σ > 0 .
Giải
Simpo PDF Merge and Split Unregistered Version - http://www.simpopdf.com
204 Giaùo Trình Vaät Lyù Ñaïi Cöông – Taäp I: Cô – Nhieät - Ñieän
Do điện tích phân bố đều trên mặt phẳng σ nên các đường sức vuông góc với
mặt phẳng, hướng ra xa mặt phẳng σ. Qũi tích của những điểm có D = const là hai mặt
phẳng đối xứng nhau qua mặt phẳng σ.
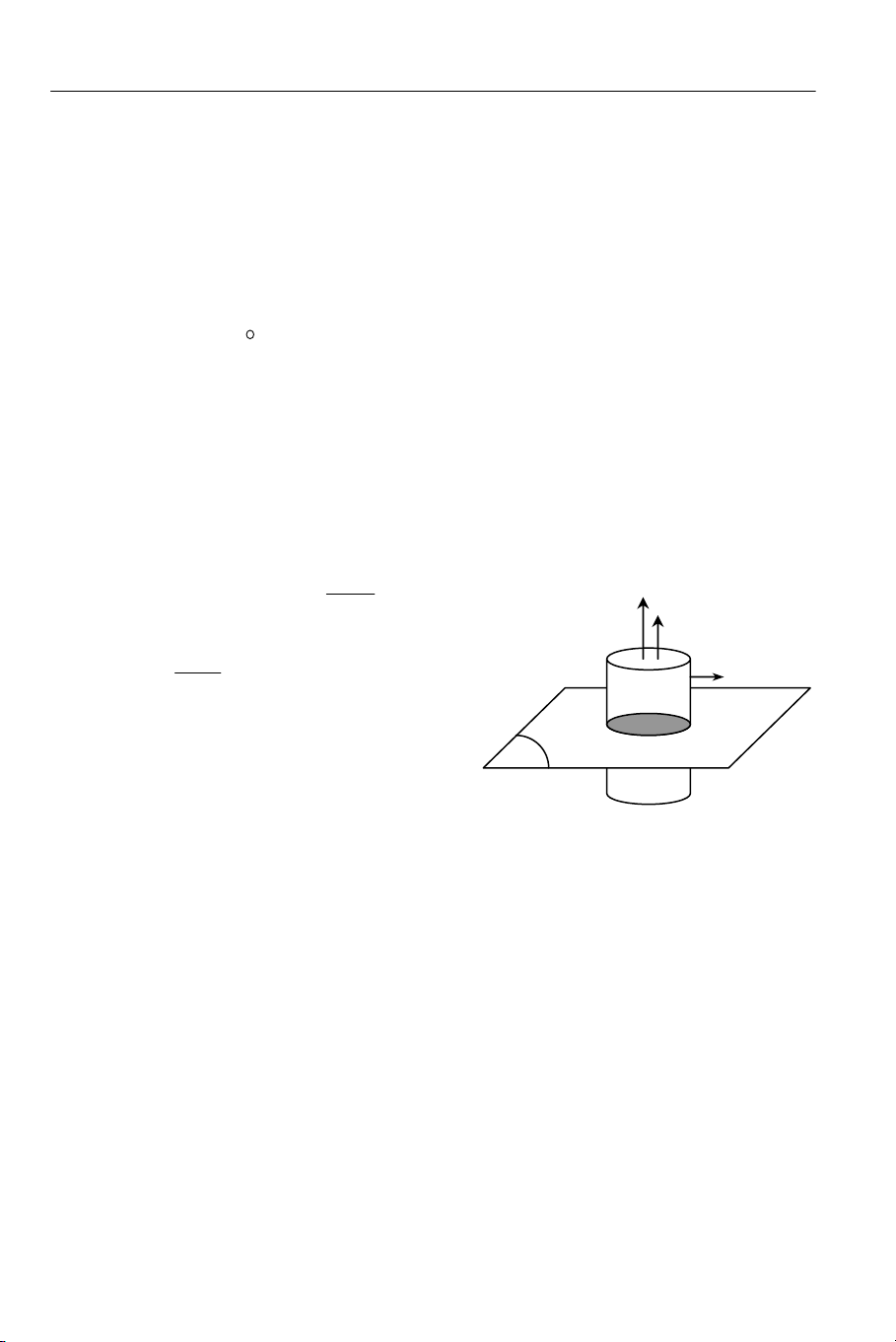
Bước 1: Chọn mặt Gauss (S) là mặt trụ có hai đáy song song, cách đều mặt phẳng σ
và chứa điểm khảo sát M, có đường sinh vuông góc với mặt phẳng σ (hình 9.14).
Bước 2: Thông lượng điện cảm gởi qua mặt Gauss là:
→→→→→→→→ ∫∫∫∫ ++==Φ Sd.DSd.DSd.DSd.D
)S(
D
döôùi ñaùytreân ñaùyquanh xung
Vì ở mặt đáy, ta có D = const và D
→→
n
↑
↑ ; còn ở mặt xung quanh thì Dn
→→
⊥
, nên ta
có: = 2εε
D0 DdS DdS2DdS2DS
ñaùy
Ñaùy treân Ñaùy döôùi ñaùy
Φ=+ + = =
∫∫ ∫ oESđáy
Mặt khác, tổng điện tích chứa trong mặt Gauss chính là tổng điện tích nằn trên tiết
diện S do mặt (σ) cắt khối trụ. Ta có Q = σ.S = σ.Sđáy
Bước 3: Vì = Q nên
D
Φ
o
2
Eεε
σ
=
n
→
S
→
D
σ
→
n
Hay 0
o
E.
2
→→
σ
=εε n (9.48)
Trong đó, là pháp vectơ đơn vị của mặt
phẳng σ. Qui ước, hướng ra xa mặt phẳng
(σ).
0
n
→
0
n
→
Hình 9.14: CĐĐT do mặt
phẳng tích điện, rộng vô
hạn, gây ra.
Nhận xét: không phụ thuộc vào vị trí điểm
khảo st, vậy điện trường do mặt phẳng tích
điện đều gây ra là điện trường đều.
→
E
Trường hợp mặt phẳng tích điện âm (σ < 0) thì (9.48) vẫn đúng. Lúc đó
hướng lại gần (σ). Kết quả (9.48) phù hợp với (9.28), tuy nhiên phương pháp
vận dụng định lí O – G thì đơn giản hơn nhiều.
→
E
Simpo PDF Merge and Split Unregistered Version - http://www.simpopdf.com

![Bài giảng Vật lý đại cương và sinh lý [mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250804/vijiraiya/135x160/88621754292979.jpg)


















![Bộ câu hỏi lý thuyết Vật lý đại cương 2 [chuẩn nhất/mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20251003/kimphuong1001/135x160/74511759476041.jpg)
![Bài giảng Vật lý đại cương Chương 4 Học viện Kỹ thuật mật mã [Chuẩn SEO]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250925/kimphuong1001/135x160/46461758790667.jpg)




