1
Chương 3
Ñònh giaù trong ñieàu
kieän coù söùc maïnh thò
tröôøng
Caùc nội dung chính
1. Phaân bieät giaù caáp moät, caáp hai, caáp ba
2. Phaân bieät giaù theo thôøi ñieåm vaø đònh
giaù luùc cao ñieåm
3. Giaû caû hai phaàn
4. Quaûng caùo
Phaân bieät giaù laø gì?
Phaân bieät giaù laø
Phaân bieät giaù là
Phaân bieät giaù laø
2
Phaân bieät giaù caáp moät
Moãi khaùch haøng coù moät möùc giaù rieâng: ñoù laø giaù
toái ña hay giaù döï kieán maø khaùch haøng saün loøng
chi traû.
Neân coøn goïi laø phaân bieät giaù caáp moät hoaøn haûo
P*
Q*
Lôïi nhuaän gia taêng töø phaân bieät giaù caáp moät
Q
$/Q Pmax
D = AR
MR
MC
Q**
PC
P*
Q*
Thaëng dö ngöôøi tieâu duøng khi
khoâng coù phaân bieät giaù
TR-TVC khi aùp duïng moät
möùc giaù duy nhaát laø P*.
Lôïi nhuaän taêng theâm do
aùp duïng chính saùch phaân
bieät giaù caáp moät hoaøn haûo
Q
$/Q Pmax
D = AR
MR
MC
Q**
PC
Lôïi nhuaän gia taêng töø phaân bieät giaù caáp moät
3
Caâu hoûi
Taïïi sao nhaø saûn xuaát laïi gaëp khoù khaên khi thöïc
hieän phaân bieät giaù caáp moät hoaøn haûo?
Traû lôøi
Phaân bieät giaù caáp moät hoaøn haûo
Phaân bieät giaù caáp moät hoaøn haûo
Moâ hình naøy chuû yeáu chöùng minh lôïi nhuaän seõ
gia taêng khi aùp duïng chính saùch phaân bieät giaù
ôû moät möùc ñoä naøo ñoù.
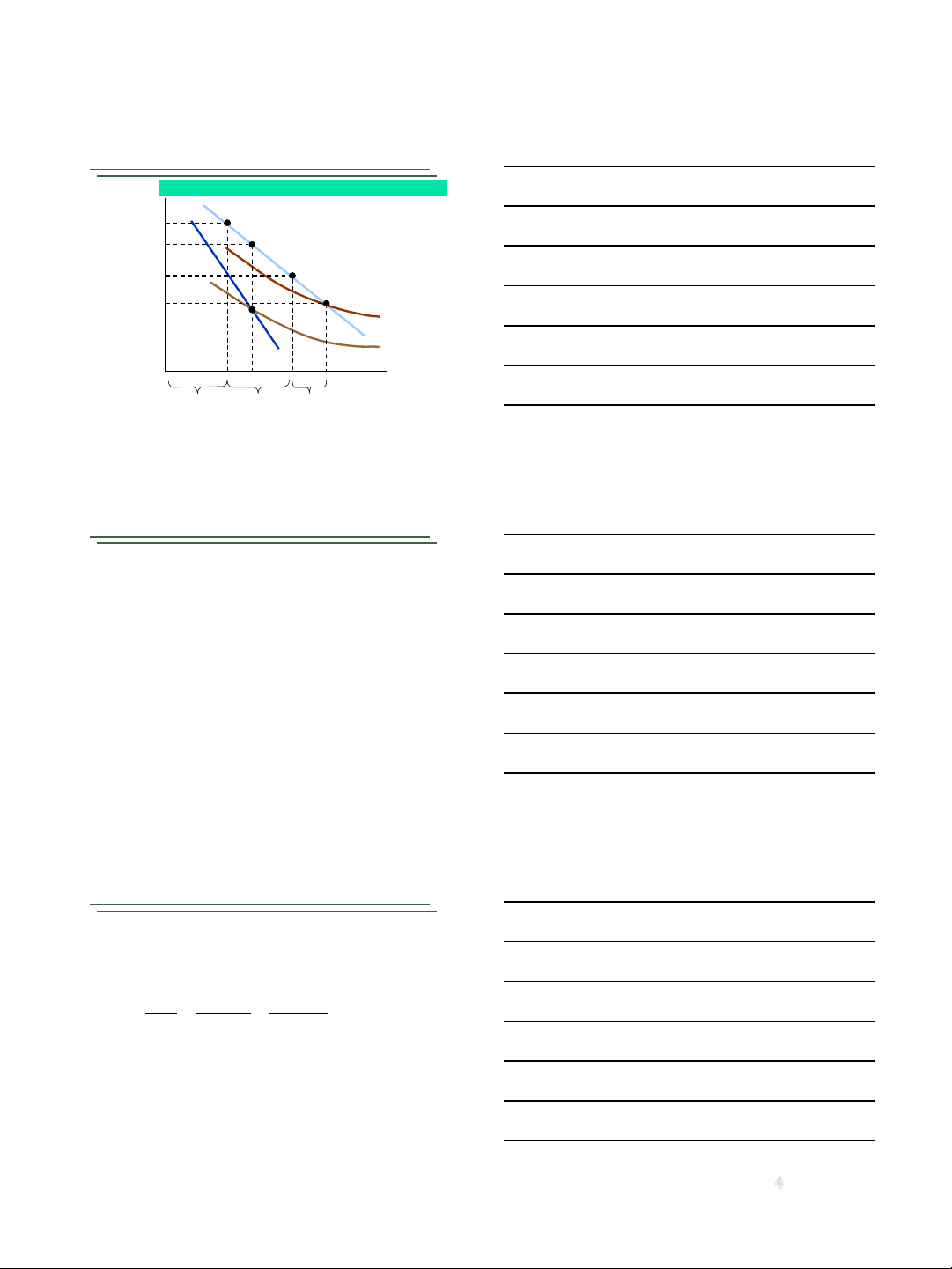
Phaân bieät giaù caáp moät trong thöïc tieãn
Q
D
MR
MC
$/Q
P2
P3
P*4
P5
P6
P1
AÙp duïng 6 möùc giaù seõ taïo ra nhieàu lôïi nhuaän
hôn nhöng moät soá khaùch haøng cuõng ñöôïc lôïi
hôn. Vôùi moät möùc giaù duy nhaát P*4, coù ít khaùch
haøng hôn vaø nhöõng ngöôøi coù theå traû möùc giaù
nhö P5 hay P6 vaãn coøn coù giaù trò thaëng dö .
Q
4
Phaân bieät giaù caáp hai
Q
$/Q
D
MR MC
AC
P0
Q0
P1
Q1
khoái 1
P2
Q2
P3
Q3
khoái 2 khoái 3
Phaân bieät giaù caáp 2 laø vieäc ñònh giaù theo löôïng haøng ñöôïc tieâu thuï
Phaân bieät giaù caáp ba
Ñieàu kieän aùp duïng phaân bieät caáp ba
1) Coâng ty phaûi coù söùc maïnh thò tröôøng.
2) Coù nhöõng nhoùm khaùch haøng khaùc nhau coù
möùc saün loøng chi traû khaùc nhau (ñoä co giaõn
cuûa caàu khaùc nhau).
3) Coâng ty phaûi coù caên cöù ñeå phaân bieät nhöõng
nhoùm khaùch haøng.
4) Ngaên chaën ñöôïc söï mua ñi baùn laïi
Ñaët phaàn gia taêng p cuûa nhoùm 1 = 0
Töông töï:
Lôïi nhuaän toái ña khi: MR1 = MR2 = MC
0
)(
(
11
)11
1
Q
QC
Q
QP
Q
T
p
MCMR  1
Phaân bieät giaù caáp ba
C(QT) = toång chi phí; QT = Q1 + Q2
Lôïi nhuaän p = P1Q1 + P2Q2 - C(QT)
MCMR  2
5
Xaùc ñònh caùc möùc giaù töông ñoái
( )
)1+1(==)1+1(= :ñoù Do
1+1= :coù Ta
222111 EPMREPMR
EPMR d
)1+1(
)1+1(
= :Vaø
1
2
2
1
E
E
P
P
Phaân bieät giaù caáp ba
Q
D2 = AR2
MR2
$/Q
D1 = AR1
MR1
MRT
MC
Q2
P2
QT
•QT : MC = MRT
•MR1 = MR2 = MC
•Nhoùm 1: P1Q1
•Nhoùm 2: P2Q2
Q1
P1
Phaân bieät giaù caáp ba
Khoâng baùn cho thò tröôøng nhoû hôn
Q
D2
MR2
$/Q
MC
D1
MR1 Q*
P*
Nhoùm moät, coù ñöôøng caàu D1, seõ khoâng saün loøng chi traû ôû
möùc giaù ñeå aùp duïng chính saùch giaù caû phaân bieät coù lôïi nhuaän.
Phaân bieät giaù caáp ba