
Giải tích 2 – Đề số 19
Câu 1: Vẽ khối
giới hạn bởi 2 2 2
4 , 2 , 2
z x x y y x y z
.
Các em tự vẽ.
Câu 2: Tìm cực trị của hàm
( , , ) 2 6 10
f x y z x y z
với điều kiện 2 2 2
35
x y z
.
Bài giải
Xét
2 2 2
, , 2 6 10
L x y z x y z x y z
'
'
1 2
'
2 2 2
2 2 0
1 1
6 2 0
1 1
3 3
10 2 0
5 5
35
x
y
z
L x
L y x x
P P
y y
L z
z z
x y z
2 2 2 2
2
d L dx dy dz
2
1
2
2
0
0
d L P
d L P
Vậy hàm f đạt cực đại tại P2(1,3,5) và cực tiểu tại P1(-1,-3,-5).
Câu 3: Khảo sát sự hội tụ của chuỗi
2
1
( 1)n
n
n n
Bài giải
Ta có:
1 1
( 1)n
n
n n
Suy ra chuỗi phân kỳ.
Câu 4:Tìm chuỗi Maclaurint của
0
ln(1 3 )
( ) x
t
f x dt
t
và tìm bán kính hội tụ của chuỗi
này.
Bài giải
Ta có:
1
1
0
0
11
2
0
(3 )
( 1)
ln(1 3 ) 3
1( 1)
1
3
( ) ( 1) ( 1)
n
nn
n n
n
n
n
n n
n
t
tn
x
t t n
f x x
n
R=1/3 theo tiêu chuẩn Cauchy
2
0
1 1
( ) ( 1)
3
( 1)
n
n
fn
hội tụ tuyệt đối
Vậy bán kính hội tụ là
1 1
3 3
x
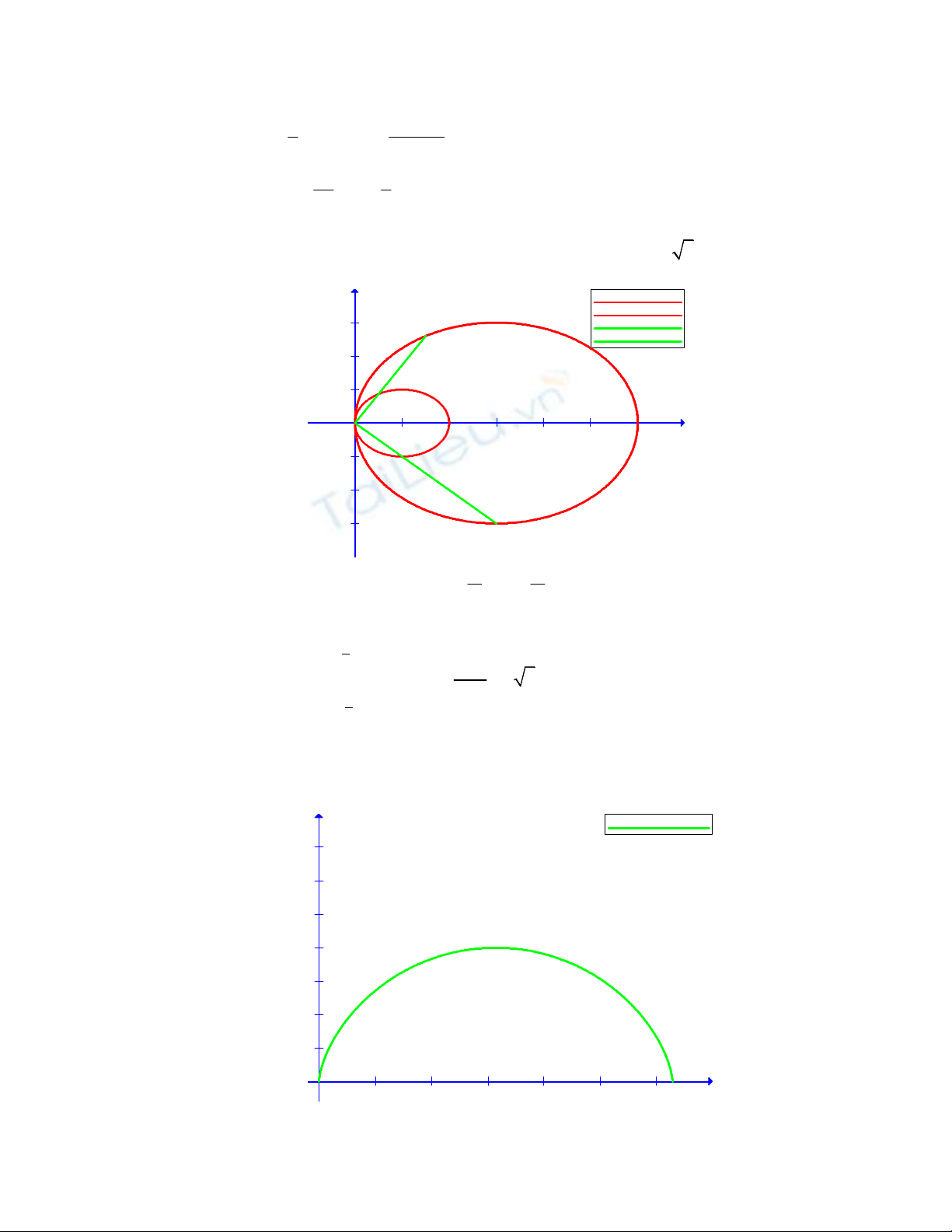
Câu 5: Tính diện tích miền phẳng giới hạn bởi 2 2
2 6 , 3, 0
x x y x y x y x
.
Bài giải
x(t)=1+cos(t) , y(t)=sin(t)
x(t)=3+3cos(t) , y(t)=3sin(t)
f(x)=-x
f(x)=x*sqrt(3)
1 2 3 4 5 6
-3
-2
-1
1
2
3
x
y
D
Đổi sang toạ độ cực: cos 4 3
sin
2cos 6cos
x r D
y r r
6cos
3
2cos
4
28
2 3 4
3
S D d rdr
Câu 6: Tính tích phân đường 2
C
I y dl
, C là cung Cycloid
( sin ), (1 cos ),0 2
x a t t y a t t
.
Bài giải
x(t)=(t-sin(t)) , y(t)=(1-cos(t ))
123456
0.5
1
1.5
2
2.5
3
3.5
x
y

Ta có:
'2 '2
2 sin
2
t t
t
x y a
2
2 2 2
0
3
(1 ost) 2 sin
2
256
15
C
t
I y dl a c a dt
a
Câu 7: Tính tích phân mặt loại hai 2
S
I z dxdy
, S là mặt trong của nửa mặt cầu
2 2 2
1 2 4, 0
x y z z
.
Bài giải
Gọi D:
2 2
1 2 4
x y
là hình chiếu của S lên mp Oxy
2 2
24 1 2
S D
I z dxdy x y dxdy
(Pháp vec tơ tạo với Oz góc tù)
2 2
2
0 0
4 8
I d r rdr


























