BÀI 1: HÀM S L NG GIÁC (TT) Ố ƯỢ
A.Muïc ñích yeâu caàu:
1.Veà kieán thöùc: -Naém vöõng baûng giaù trò LG cuûa caùc cung ñaëc bieät-caùch tìm TXÑ cuûa caùc HSLG-Tính ñöôïc caùc
giaù trò LG ,söï bieán thieân cuûa ñoà thò HSLG
2.Veà kó naêng: -Thaønh thaïo caùc kieán thöùc treân,(chú ý cách tìm TXĐ c a hàm s LG)ủ ố
3.Veà thaùi ñoä: - Nghieâm tuùc phaùt bieåu vaø xaây döïng baøi-
B.Chuaån bò: GV: giaùo aùn ,SGK,maùy tính casio……; HS: SGK, thöôùc keõ, maùy tính casio …….
C.Phöông phaùp:- Neâu vaán ñeà ( Gôïi môû )
D.Tieán trình leân lôùp: 11CA
tg Hoaït ñoäng thaày Hoaït ñoäng troø Noäi dung kieán thöùc
15
’
-Nhaéc laïi
Rxkx ∈∀=+ ?)2sin(
π
-Goïi hsinh leân baûng trình baøy
-GV nhaän xeùt vaø ñaùnh giaù
-Döïa vaøo söï bieán thieân cuûa ñoà thò
haøm soá y=sinx
-Goïi 1hsinh trình baøy söï bieán thieân
cuûa ñoà thò haøm soá y=cosx
-Haøm soá y= cosx coù:
+TXÑ?
+Chu kì T=? ;k/s töø ñaâu tôùi ñaâu?
+Laø haøm soá chaün hay haøm soá
leû?
-Cho hsinh ñöùng taïi choå traû lôøi
Baûng bieán thieân?
x 0
2
π
π
y=cosx ?
-Cho hsinh ñöùng taïi choå traû lôøi
-GV nhaän xeùt vaø ñaùnh giaù
-Nhìn vaøo ñoà thò beân haõy cho bieát
ñoà thò beân ñoàng bieán ,nghòch bieán
treân ñaâu?
-Cho hsinh ñöùng taïi choå traû lôøi
HS1:
Rxxkx ∈∀=+ sin)2sin(
π
HS2:
+TXÑ: D=R
+Chu kì
π
2=T
+laø haøm soá chaün
HS3:
1cos
10cos
0
2
cos
−=
=
=
π
π
-Hsinh xung phong
BAØI 1:HAØM SOÁ LÖÔÏNG GIAÙC
III.SÖÏ BIEÁN THIEÂN VAØ ÑOÀ THÒ CUÛA
HAØM SOÁ LG
2.Haøm soá y=cosx
*TXÑ:
)( RxRD ∈∀=
*TGT:
*Haøm soá tuaàn hoaøn vôùi chu kì
π
2
=
T
Khaûo saùt treân
[ ]
ππ
;−
*Haøm soá chaün vì cos(-x)=cosx
Do ñoù ta chæ khaûo saùt haøm soá y=sinx treân
[ ] [ ]
0;;0
ππ
−⇒
+K/s haøm soá y=cosx nb treân
[ ]
π
;0
+Baûng bieán thieân:
Ngaøy soaïn: 21/8/09
Ngaøy daïy:
……………….
Lôùp : …11CA
Tieát PPCT :3.
0
y=cosx 1 0
--1
20
’
5’
5’
-GV nhaän xeùt vaø ñaùnh giaù chung
-Vôùi
?)2cos( =+
π
kx
neáu k=3
-Cho hsinh thaûo luaän traû lôøi
NI: ñ/v k=4 hoaëc k= -3
NII: ñ/v k=-4 hoaëc k= 3
-GV nhaän xeùt vaø ñaùnh giaù
-Haøm soá y=tanx coù:
+TXÑ?
+ Tuaàn hoaøn vôùi chu kì?
+ Laø haøm soá chaün hay haøm soá
leû?
-Cho hsinh ñöùng taïi choå traû lôøi
+Baûng bieán thieân:
x 0
2
π
π
y=tanx ?
-GV minh hoaï ñoà thò sau ñoù cho hsinh
nhaän bieát tính tuaàn hoaøn cuûa ñoà
thò haøm soá y=tanx
-Nhìn vaøo ñoà thò khi x caøng gaàn
2
π
NI: trình baøy
NII: trình baøy
HS5:
+TXÑ:
∈+= ZkkRD ,
2
\
π
π
+
π
=
T
HS6:
||
2
tan
00tan
1
4
tan
=
=
=
π
π
(||: khoâng xaùc ñònh)
HS7:
-Khi x caøng gaàn
2
π
thì ñoà thò y=tanx
caøng gaàn ñöôøng thaúng
2
π
=
x
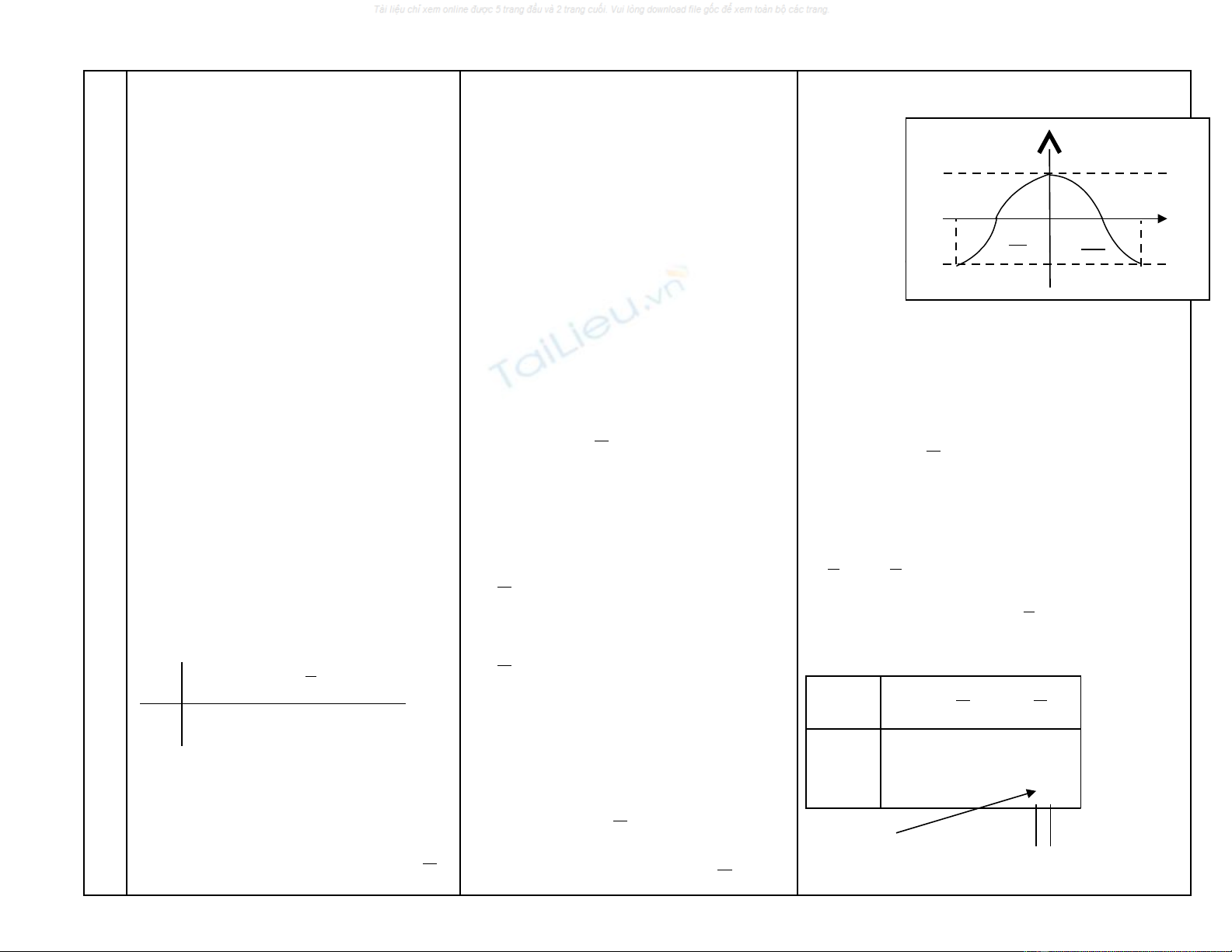
+Ñoà thò:
Vaäy haøm soá y=cosx laø haøm soá chaün
neân ñoà thò nhaän truïc tung laøm truïc ñoái
xöùng.
*Chuù yù:
)(cos)2cos( Zkxkx ∈=+
π
Haøm soá y=sinx vaø y=cosx goïi chung laø caùc ñöôøng
hình sin
3.Haøm soá y=tanx
+TXĐ:
∈+= ZkkRD ,
2
\
π
π
+TGT:
( )
+ ∞∞− :
+ Là hàm s l vì tan(-x)=-tanx v i ố ẻ ớ
Dx
∈∀
+ Là hàm s tu n hoàn v i chu kì ố ầ ớ
π
=T
ta kh o sát tả ừ
−⇒
0;
22
;0
ππ
+ Hàm s y = tanx ố ñoàng bi n ế
2
;0
π
*B ng bi n thiên:ả ế
2
π
−
π
O
π
−
2
π
1
y
x
1
−
x0
4
π
2
π
y =tanx
∞+
1
0
5’
thì ñoà thò y=tanx ntn?
-Cho hsinh thaûo luaän suy nghó ?giaûi thích?
-GV nhaän xeùt chung
Ví duï: T p Xác đ nh hàm s y = cotx là:ậ ị ố
a)
{ }
ZkkRD ∈= ,\
π
b)
{ }
ZkkxRD ∈≠= ,\
π
c)
RD =
d)
∈+== ZkkxRD ,
2
\
π
π
-Haõy choïn phöông aùn ñuùng
-GV nhaän xeùt vaø ñaùnh giaù
*CUÛNG COÁ:
-Naém vöõng söï bieán thieân cuûa haøm soá
y=cosx vaø y=tanx
-TGT,chu kì cuûa hai haøm soá treân
-Caùch nhaän bieát ñoà thò-tính ñöôïc caùc giaù trò
cuûa HSLG
-Chuaån bò baøi hoïc tieáp theo
-Hsinh chuù yù
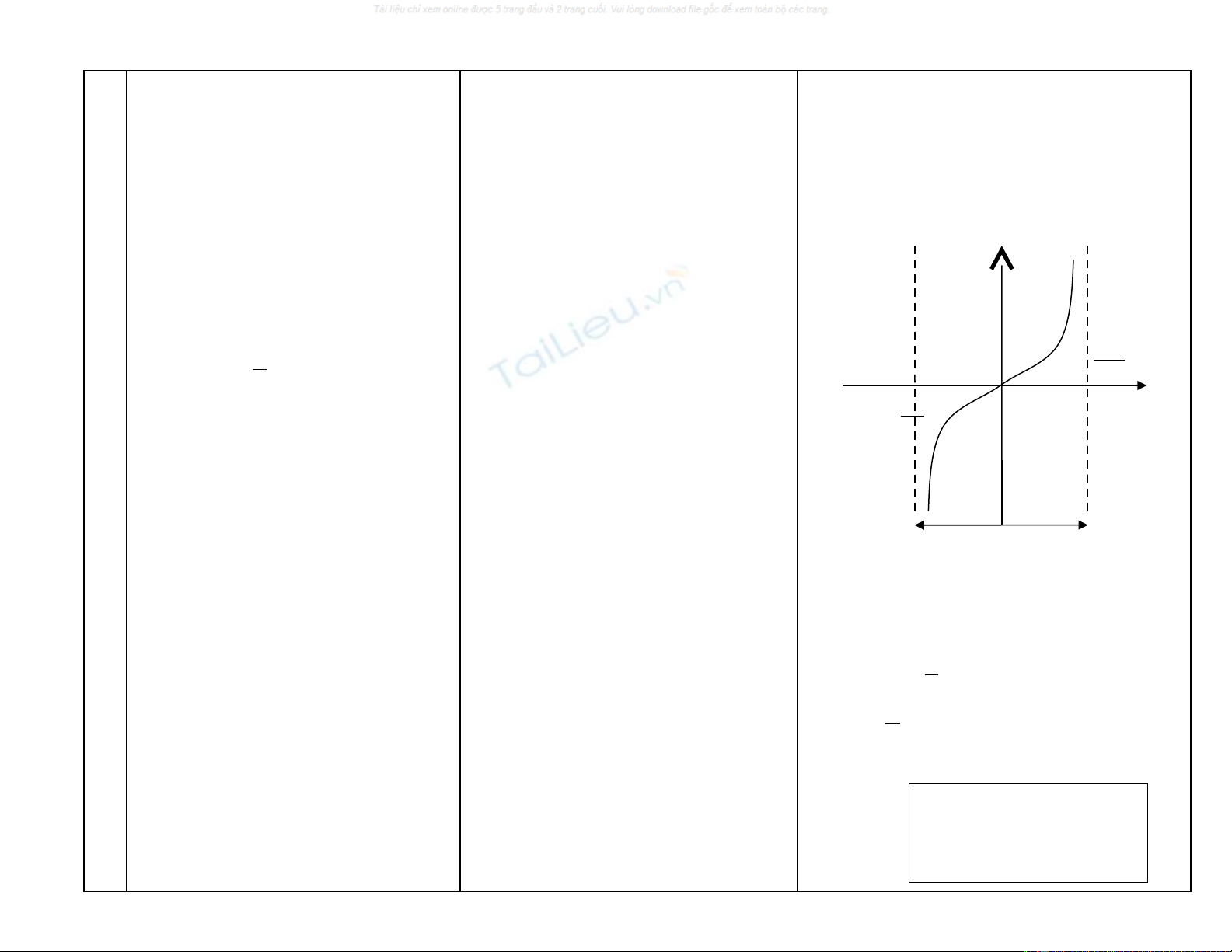
*Đ th hàm s :ồ ị ố
*Nhaän xeùt:
Nhìn vào đ th ta th y hàm s y = tanx ồ ị ấ ố laø haøm soá leû
neân nhận goùc toaï ñoâï laøm taâm ñoái xöùng
-Khi x caøng gaàn
2
π
thì ñoà thò y=tanx caøng gaàn ñöôøng
thaúng
2
π
=
x
y
0
2
π
−
2
π
x
T
Kyù duyeät: 22/8/2009
HĐ1: Tìm TXĐ của hàm số sau:
a)
x
x
ycos
sin1+
=
b)
)
6
2tan(
π
−= xy
-Gọi 2 em Hsinh lên bảng trình bày (cácem còn lại
làm nháp và nhận xét)
-GV nhận xét và đánh giá chung
-Cho Hsinh lên bảng tính các giá trị của hàm số
trên
-Gv nhận xét và đánh giá
CÂU HỎI TRẮC NGHIỆM
Câu 1:Chọn câu đúng nhất:
)(,?)cot( Zkkx ∈=+
π
a) cotx b) tanx c) sinx d) cosx
Câu 2:
?
2
cot =
π
a) 1 b) 0 c) không xác định d) -1
Câu 4: Chu kì của hàm số
2
2cos1 x
y+
=
a)
π
b)2
π
c) 4
π
d) 3
π
Câu 5 Hàm số y =cosx đồng biến trên
a)
( )
π
:0
b)
( )
0:
π
−
c)
( )
ππ
:−
d)
−2
;
2
ππ
y
0
π
2
π
π
2
2
3
π
x
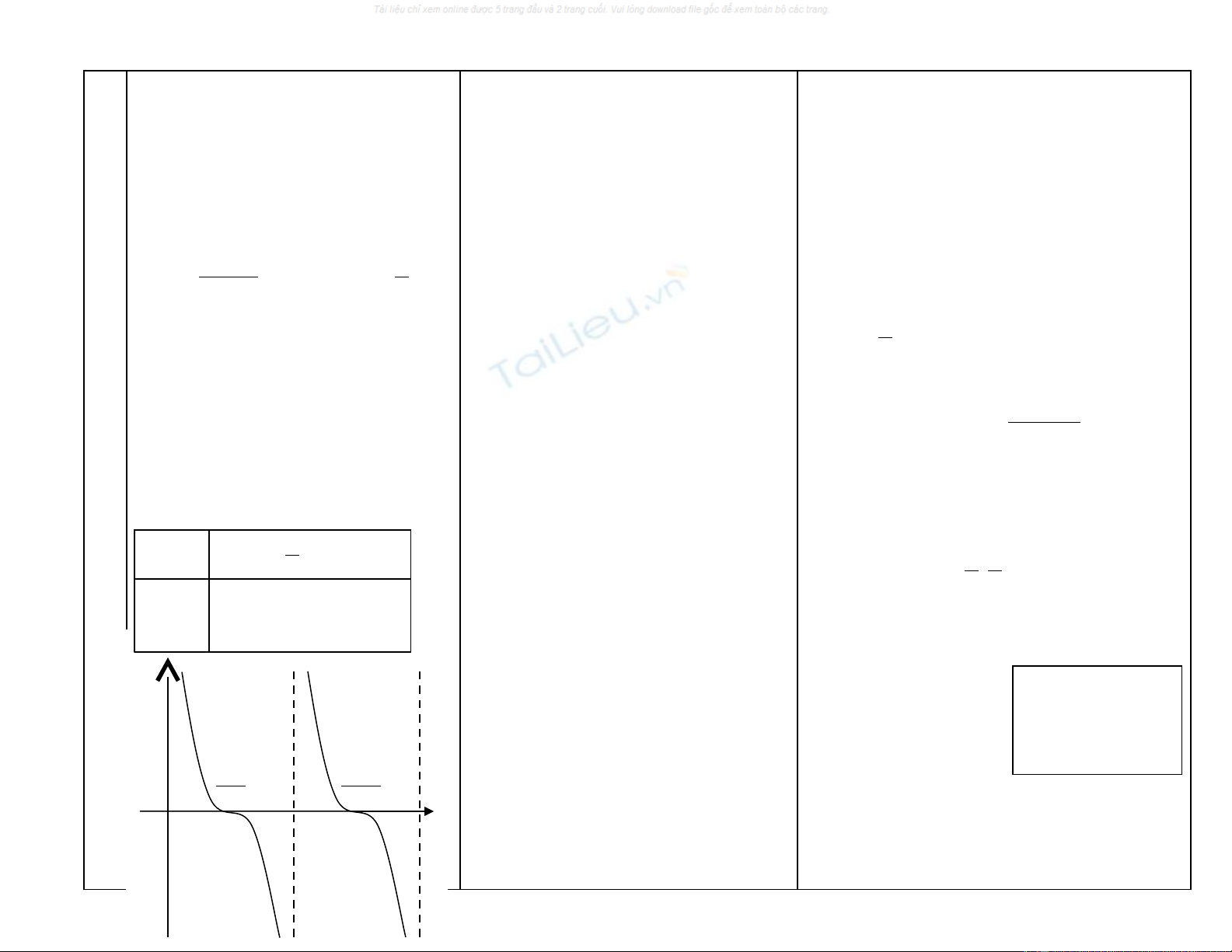
x0
2
π
π
y =cotx
?
Kyù duyeät
Nhìn vào đồ thị các em nhận xét gì về các nhánh
của đồ thị và đường tiệm cận đứng
-Cho Hsinh đứng tại chổ trả lời
-Câu hỏi trắc nghiệm ,GV chia lớp ra thành 4
nhóm
NI: Câu 1 ,5
NII: Câu 2,5
NIII: Câu 3.5
NIV: Câu 4,5
-Cho Hsinh đại diện nhóm lên bảng trình bày
-GV nhận xét và đánh giá chung
*CỦNG CỐ:
-Nắm vững cách tìm TXĐ của hàm số lượng giác
-Chu kì của hàm số LG(tính chẵn lẻ của HSố)
-Các bước vẽ đồ thị hàm số y = cotx
-Sự biến thiên của HSLG (y=cotx)
-Làm bài tập 1-8 sgk (trang 17-18)
HS1:a) Hàm số
x
x
ycos
sin1+
=
xác định khi
Zkkxx ∈+≠⇔≠ ,
2
0cos
π
π
Vậy TXĐ:
∈+= ZkkRD ,
2
\
π
π
HS2
Với x=0 thì
+ ∞=
y
Với
π
=x
thì
−∞=y
Với
2
π
=x
thì y=0