Chuyên đ t ch n: ề ự ọ QUAN H VUÔNG GÓC TRONG KHÔNG GIANỆ
I.M c tiêu:ụ
Qua ch đ này HS c n:ủ ề ầ
1)V Ki n th c:ề ế ứ Làm cho HS hi u sâu s c h n v ki n th c c b n vể ắ ơ ề ế ứ ơ ả ề
quan h vuông góc trong không gian.ệ
2)V k năng:ề ỹ Tăng c ng rèn luy n k năng gi i toán v quan h vuôngườ ệ ỹ ả ề ệ
góc trong không gian. Thông qua vi c rèn luy n gi i toán HS đ c c ng c m t sệ ệ ả ượ ủ ố ộ ố
ki n th c đã h c trong ch ng trình.ế ứ ọ ươ
3)V t duy và thái đ :ề ư ộ
Tích c c ho t đ ng, tr l i câu h i. Bi t quan sát và phán đoán chính xác.ự ạ ộ ả ờ ỏ ế
Làm cho HS h ng thú trong h c t p môn Toán.ứ ọ ậ
II. CHU N B :Ẩ Ị
1) chu n b c a h c sinh: h c bài cũ và n m ch c các khái ni m, đ nh lí đãẩ ị ủ ọ ọ ắ ắ ệ ị
đ c h cượ ọ
2) chu n b c a giáo viên: các ví d mang tính khái quát ph ng pháp.ẩ ị ủ ụ ươ
III. TI N TRÌNH BÀI H C:Ế Ọ
Ho t đ ng c a giáo viênạ ộ ủ Ho t đ ng c a h cạ ộ ủ ọ
sinh
Ghi b ngả
Giáo viên nêu đ và về ẽ
hình lên b ng cho hs suyả
nghĩ và sau đó g i ý h cợ ọ
sinh gi i.ả
- Đ ch ng minh m tể ứ ộ
đ ng th ng vuông gócườ ẳ
v i m t m t ph ng thì taớ ộ ặ ẳ
c n ch ng minh gì?ầ ứ
- T đó áp d ng ch ngừ ụ ứ
minh bài trên.
Chú ý lên b ng và suyả
nghĩ gi i bài toán.ả
- Đ ch ng minh m tể ứ ộ
đ ng th ng vuôngườ ẳ
góc v i m t m tớ ộ ặ
ph ng thì ta ch ngẳ ứ
minh đ ng th ng đóườ ẳ
vuông góc v i 2 đ ngớ ườ
th ng c t nhau n mẳ ắ ằ
trong m t ph ng đó.ặ ẳ
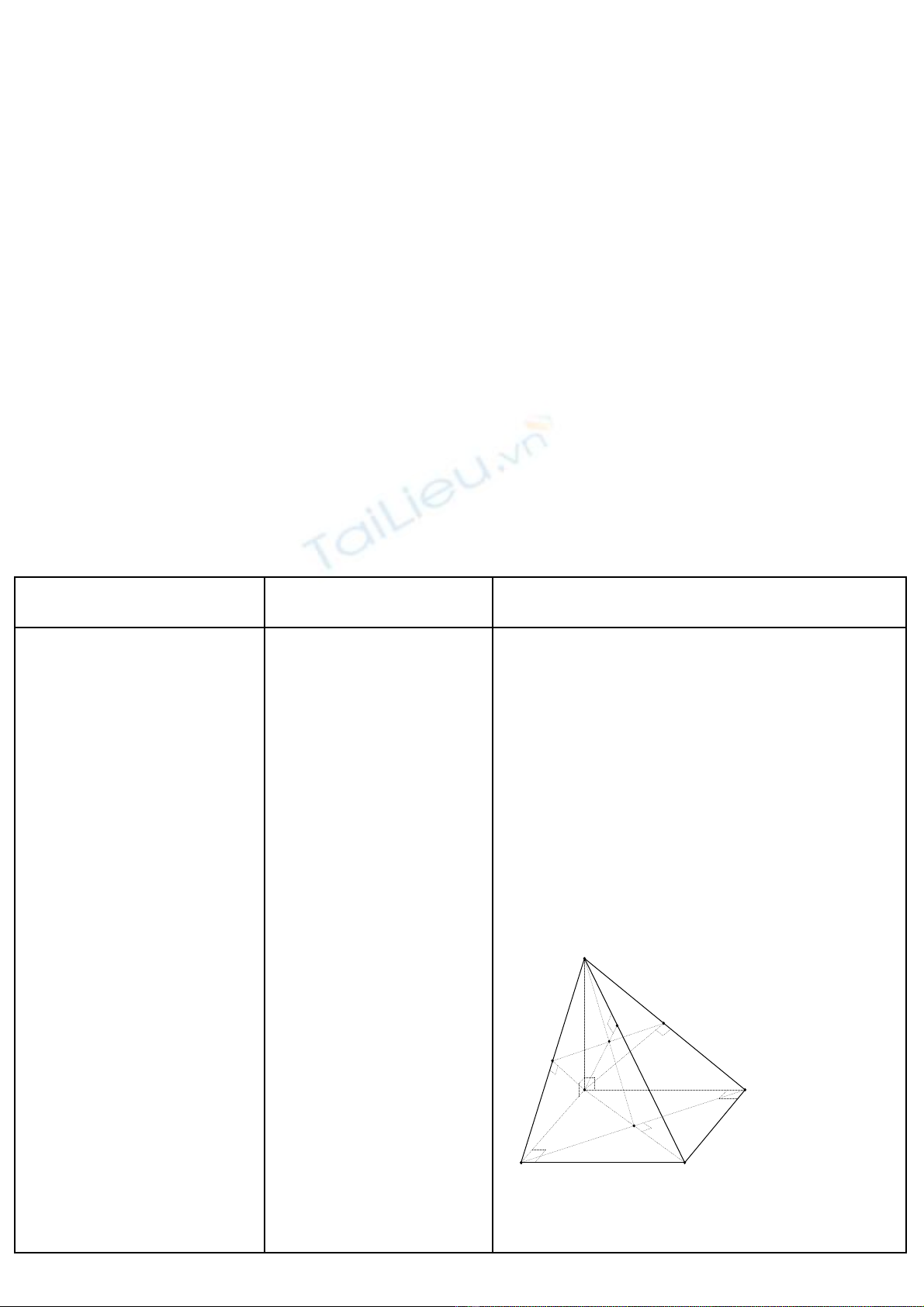
Bài 1. Cho hình chóp S.ABCD có đáy
ABCD là hình vuông tâm O; SA ⊥ (ABCD).
G i H, I, K l n l t là hình chi u vuôngọ ầ ượ ế
góc c a A lên SB, SC, SD.ủ
a) CMR: BC ⊥ (SAB); CD ⊥ (SAD); BD ⊥
(SAC).
b) CMR: AH ⊥ SC; AK ⊥ SC. T đó suy raừ
AH, AI, AK đ ng ph ng.ồ ẳ
c) CMR: HK ⊥ (SAC); HK ⊥ AI
Gi i:ả
A
B
D
C
S
H
K
I
a)
Đ c/m BC ể⊥ (SAB) ta
s c/m BC vuông góc v iẽ ớ
2 đ ng th ng c t nhauườ ẳ ắ
n m trong (SAB) là SAằ
và AB. G i hs c/m vàọ
t ng t cho nh ng ýươ ự ữ
sau.
b) Đ c/m 2 đ ng th ngể ườ ẳ
vuông góc v i nhau taớ
th ng c/m 1 đ ngườ ườ
th ng vuông góc v i m tẳ ớ ặ
ph ng ch a đ ng th ngẳ ứ ườ ẳ
kia.
- Nh đ c/m AH ư ể ⊥ SC ta
c/m AH ⊥ (SBC) ⊃ SC.
G i hs lên b ng gi i và c/ọ ả ả
m t ng t cho các ýươ ự
khác
c)
Đ c/m 1 đ ng th ngể ườ ẳ
vuông góc v i 1 m tớ ặ
ph ng ta còn cách khác làẳ
c/m đ ng th ng đó //ườ ẳ
v i 1 đ ng th ng khác //ớ ườ ẳ
v i m t ph ng.ớ ặ ẳ
a)
i/ c/m: BC ⊥ (SAB)
- Vì SA ⊥ (ABCD) và BC ⊂ (ABCD) nên
SA ⊥ BC (1)
- M t khác có ABCD là hình vuông nên ABặ
⊥ BC (2)
- Mà SA, AB ⊂ (SAC) Và SA ∩ AB = A
(3)
T (1), (2) và (3) ừ⇒ BC ⊥ (SAB)
ii/ CD ⊥ (SAD)
T ng t cho các ý khácươ ự
- CD ⊥ AD (ABCD là hình vuông)
- CD ⊥ SA (SA ⊥ (ABCD))
- AD, SA ⊂ (SAD), SA ∩ AD = A
⇒ CD ⊥ (SAD)
iii/ BD ⊥ (SAC)
- BD ⊥ AC (2đ ng chéo c a hìnhườ ủ
vuông)
- BD ⊥ SA (SA ⊥ (ABCD))
- AC, SA ⊂ (SAC), SA ∩ AC = A
⇒ BD ⊥ (SAC)
b)
- c/m: AH ⊥ SC
+ Theo câu a) ta có BC ⊥ (SAB)
mà AH ⊂ (SAB) nên BC ⊥ AH
+ Theo gt SB ⊥ AH
+ SB, BC ⊂ (SBC), SB ∩ BC = B
⇒ AH ⊥ (SBC) mà SC ⊂ (SBC)
V y AH ậ⊥ SC
- c/m AK ⊥ SC :
+ Theo câu a) ta có CD ⊥ (SAD)
mà AK ⊂ (SAD) nên CD ⊥ AK
+ Theo gt SD ⊥ AK
+ SD, CD ⊂ (SCD), SD ∩ CD = D
⇒ AK ⊥ (SCD) mà SC ⊂ (SCD)
V y AH ậ⊥ SC
c)
- c/m: HK ⊥ (SAC) và HK ⊥ AI
+ Hai tam giác vuông ∆SAB = ∆SAD
+ AH, AK là các đ ng cao c a 2 tam giácườ ủ
t A.ừ
suy ra = ⇒ HK // BD
Theo c/m câu a) BD ở⊥ (SAC)
- ý c đ c/m HK ở ể ⊥
(SAC) ta c/m HK // BD.
G i hs gi iọ ả
V y HK ậ⊥ (SAC)
Vì AI ⊂ (SAC) nên HK ⊥ AI
Bài 2: bài này ph ngở ươ
pháp gi i hoàn toànả
t ng t bài 1. gv vươ ự ẽ
hình và g i ý cho hs suyợ
nghĩ tìm ra l i gi i.ờ ả
a)
- Đ c/m CI ể⊥ SB ta s c/ẽ
m CI vuông góc v i m tớ ộ
m t ph ng ch a SB. G iặ ẳ ứ ọ
hs đ ng t i ch ch raứ ạ ỗ ỉ
m t ph ng đó là m tặ ẳ ặ
ph ng nào?và cho hs đóẳ
lên b ng trình bày.ả
- T ng t cho vi cươ ự ệ
c/m DI ⊥ SC ta sẽ
c/m DI ⊥ (SAC).
G i hs b t kì làmọ ấ
ti p.ế
c) c/m các m t bên là cácặ
tam giác vuông th c ch tự ấ
c a bài toán cũng là c/m 2ủ
đ ng th ng vuông gócườ ẳ
v i nhau. Nh ng khóớ ư
khăn đây là ch a bi t 2ở ư ế
đ ng th ng nào vuôngườ ẳ
góc v i nhau.ớ
Hs quan sát và tìm l iờ
gi i. tìm m t ph ngả ặ ẳ
ch a đ ng th ng c nứ ườ ẳ ầ
ch ng minh thích h pứ ợ
a)
- Ta s c/m CI ẽ⊥ (SAB)
- Nghe h ng d n vàướ ẫ
lên b ng trình bày. ả
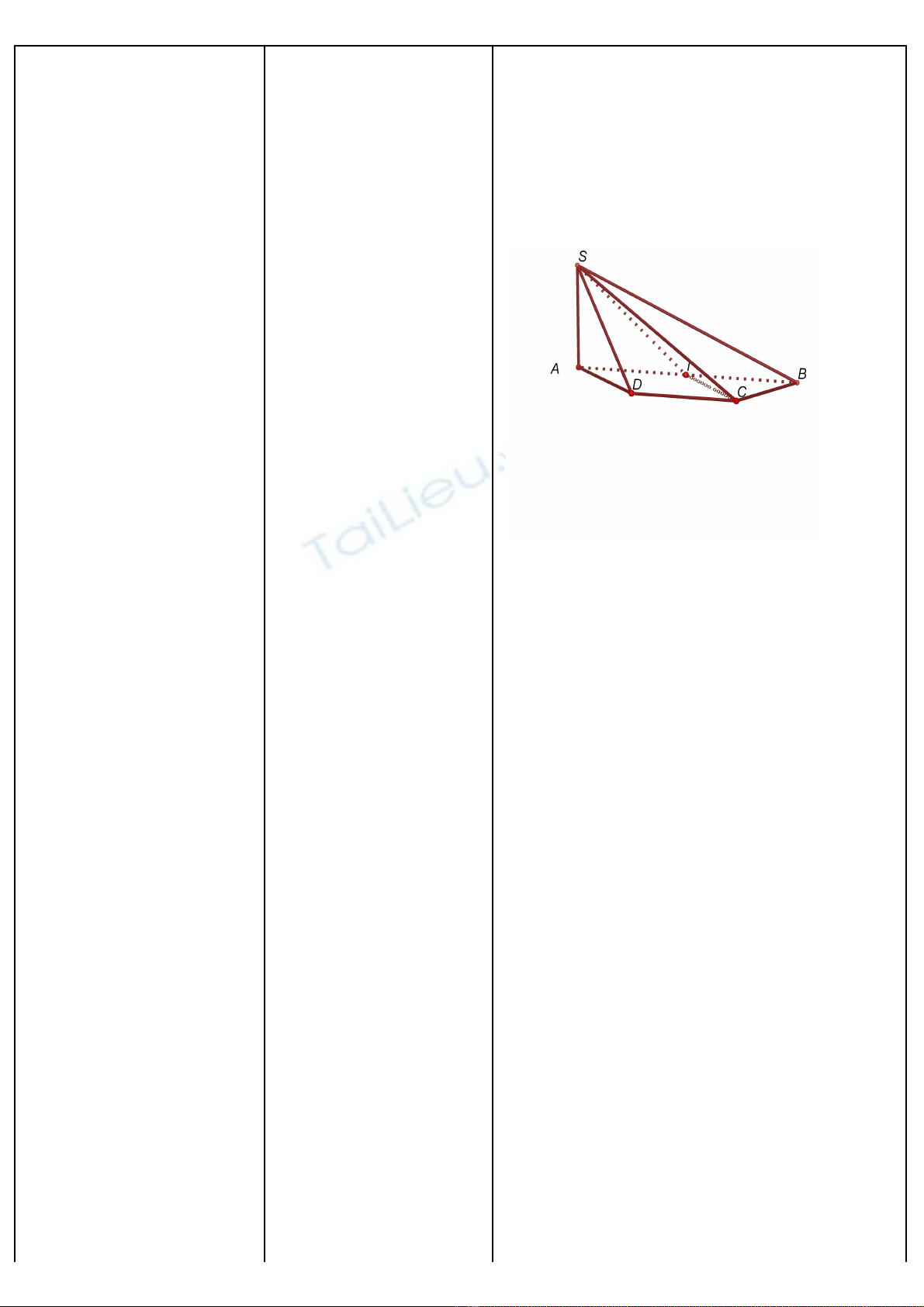
Bài 2: Cho hình chóp SABCD có đáy ABCD
là hình thang vuông t i A, D và SA = a, SAạ
vuông góc (ABCD), AB =2a, AD = DC = a.
G i I là trung đi m c a ABọ ể ủ
a) CMR: CI ⊥ SB, DI ⊥ SC
b) CMR: Các m t bên c a hình chópặ ủ
SABCD là các tam giác vuông
Gi i: ả
a)
- c/m CI ⊥ SB:
+ theo gt SA ⊥ (ABCD) mà CI ⊂ (ABCD)
nên SA ⊥ CI (1)
+ xét t giác ADCI có AI = AD = DC = aứ
và = = 90 nên ADCI là hình vuông. T đóừ
suy ra AB ⊥ CI (2)
+ SA, AB ⊂ (SAB), SA ∩ AB = A (3)
T (1), (2) và (3) suyb ra CI ừ⊥ (SAB) mà SB
⊂ (SAB)
V y CI ậ⊥ SB (đpcm)
- c/m DI ⊥ SC:
+ AC ⊥ DI (vì 2 đ ng chéo c a hình vuôngườ ủ
ADCI) (4)
+ theo gt SA ⊥ (ABCD) mà DI ⊂ (ABCD)
nên SA ⊥ DI (5)
+ SA, AC ⊂ (SAC) SA ∩ AC = A (6)
T (4), (5) và (6) suy ra DI ừ⊥ (SAC)
Mà SC ⊂ (SAC) nên DI ⊥ SC (đpcm)
c) - các m t bên SAB, SAD vuông t i Aặ ạ
theo gt
- SCD vuông t i D ạ
- SBC vuông t i C (tính đ dài các c nh)ạ ộ ạ
Bài 3: Đây coi nh là bàiư
t p c ng c l i cácậ ủ ố ạ
ph ng pháp c/m 2ươ
đ ng th ng vuông gócườ ẳ
và đ ng th ng vuôngườ ẳ
góc v i m t ph ng. Gvớ ặ ẳ
ch nêu đ và cho hs gi iỉ ề ả
quy t bài toán.ế
Suy nghĩ và gi i bàiả
toán b ng các ph ngằ ươ
pháp v a đ c sừ ượ ử
d ng bài 1 và bài 2ụ ở
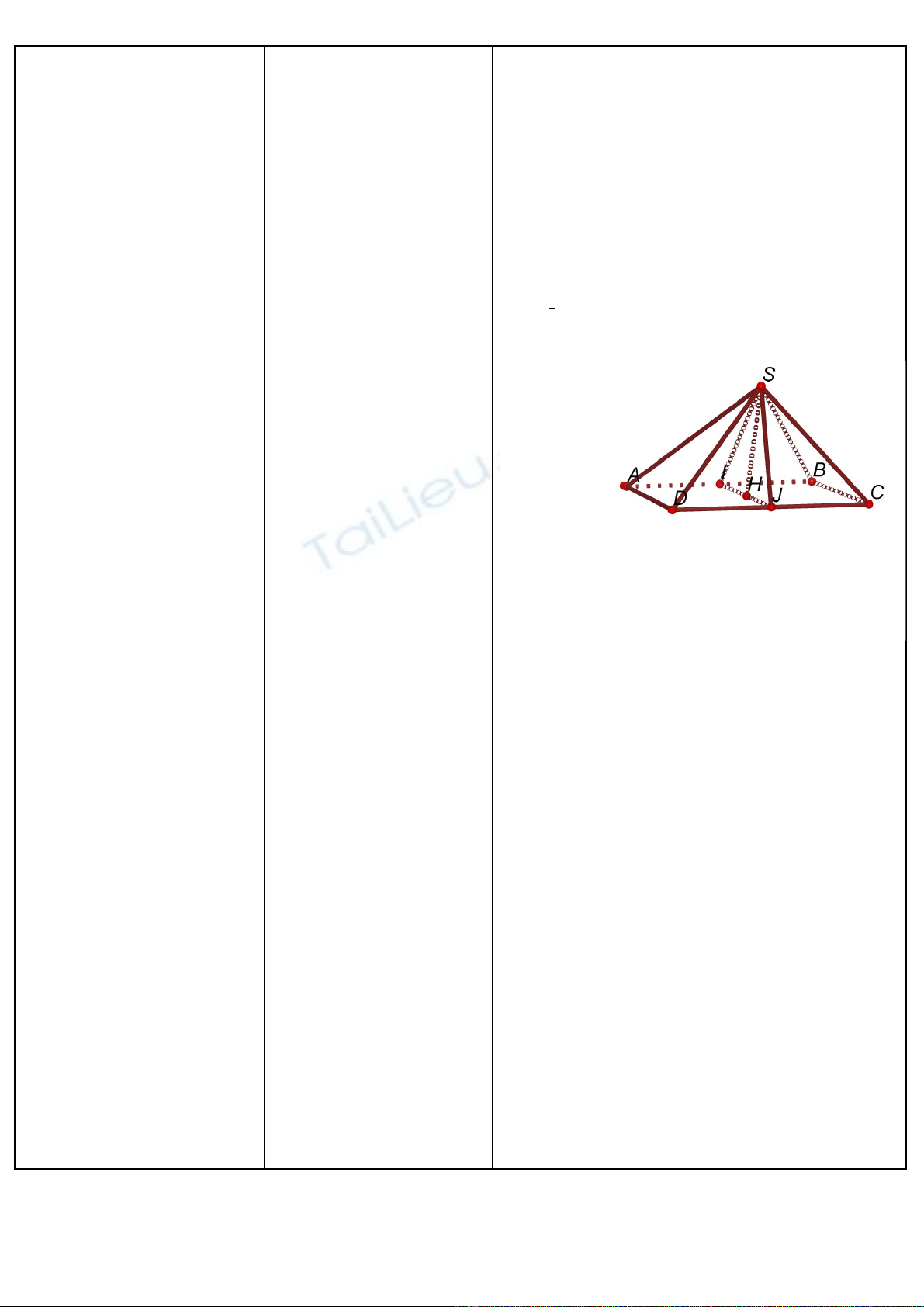
Bài 3: Cho hình chóp S.ABCD có đáy
ABCD là hình vuông c nh a. ạ∆SAB đ u;ề
∆SCD vuông cân đ nh S. I, J l n l t làỉ ầ ượ
trung đi m c a AB, CD.ể ủ
a) Tính các c nh c a ạ ủ ∆SIJ.
CMR: SI ⊥ (SCD); SJ ⊥ (SAB)
b) G i H là hình chi u vuông góc c a S lênọ ế ủ
IJ.
CMR: SH ⊥ AC
gi i: ả
a) - Tính các c nh c a ạ ủ ∆SIJ
+ xét ∆SAI vuông t i I nên SI = ạ
+ IJ = AD = a
+ = + Mà SC = SD =
Suy ra SJ =
- c/m SI ⊥ (SCD)
+ T trên ta có IJ = SI + SJ nên ừ∆SIJ vuông
t i S. suy ra SI ạ⊥ SJ (1)
+ SI ⊥ CD (2)
+ SJ, CD ⊂ (SCD), SJ ∩ CD = J (3)
Suy ra SI ⊥ (SCD)
b) c/m SH ⊥ AC
- c/m SH ⊥ (ABCD) b ng cách ch ng minhằ ứ
SH vuông góc v i 2 đ ng th ng c t nhauớ ườ ẳ ắ
n m trong m t ph ng(ABCD). đâyta l yằ ặ ẳ ở ấ
2 đ ng th ng là IJ và CD. G i hs c/mườ ẳ ọ
+ SH ⊥ IJ (gt)
+ SH ⊥ CD (CD ⊥ (SIJ) ⊃ SH)
+ IJ ∩ CD = H
Suy ra SH ⊥ (ABCD) ⊃ AC ⇒ SH ⊥ AC
C ng c : - gv nêu l i các ph ng pháp c/m 2 đ ng th ng vuông góc, đ ngủ ố ạ ươ ườ ẳ ườ
th ng vuông v i m t ph ngẳ ớ ặ ẳ