Giáo án Tự động hóa và điều khiển thiết bị điện: Chương 3

Chia sẻ: Trinh _ | Ngày: | Loại File: PDF | Số trang:26

Thêm vào BST

Báo xấu

49
lượt xem 4
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Giáo án Tự động hóa và điều khiển thiết bị điện: Chương 3 - Điều khiển dùng phần tử không tiếp điểm giới thiệu về đại số logic, các cổng logic cơ bản, các cổng logic khác, phương pháp thiết kế sơ đồ mạch logic,... Mời các bạn tham khảo!

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Giáo án Tự động hóa và điều khiển thiết bị điện: Chương 3

Ch-¬ng 3: §iÒu khiÓn dïng phÇn tö kh«ng tiÕp ®iÓm (8 tiÕt) 3.1 §¹i sè logic. 3.1.1. Kh¸i niÖm vÒ ®¹i sè logic §¹i sè logic ®-îc hiÓu lµ mét tËp hîp Y cña c¸c ®èi t-îng (c¸c biÕn) A, B, C.... trong ®ã x¸c ®Þnh hai phÐp tÝnh logic céng (+) vµ nh©n (.). C¸c biÕn logic cã hai tr¹ng th¸i: cã hoÆc kh«ng, mÖnh ®Ò ®óng hoÆc sai. Khi tr¹ng th¸i cña ®èi t-îng lµ cã ta g¸n cho biÕn logic biÓu diÔn nã gi¸ trÞ quy -íc lµ 1 vµ ký hiÖu lµ A, cßn khi tr¹ng th¸i cña ®èi t-îng lµ kh«ng ta g¸n cho nã gi¸ trÞ quy -íc 0 vµ ký hiÖu lµ A om Gi÷a c¸c biÕn logic, ng-êi ta ®Þnh nghÜa ba phÐp to¸n c¬ së: - PhÐp phñ ®Þnh (phÐp ®¶o) logic ®èi víi mét biÕn logic A nµo ®ã lµ khi t¸c .c ®éng phÐp to¸n nµy A sÏ nhËn gi¸ trÞ ®¶o cña gi¸ trÞ ban ®Çu vµ ký hiÖu lµ A . ng - PhÐp céng logic (phÐp hoÆc) ®-îc ký hiÖu b»ng dÊu "+". VÝ dô A + B lµ phÐp céng gi÷a hai biÕn logic A vµ B, mçi biÕn ®-îc gäi lµ co mét sè h¹ng vµ kÕt qu¶ gäi lµ mét tæng. - PhÐp nh©n logic (phÐp vµ) ®-îc ký hiÖu b»ng dÊu ".". 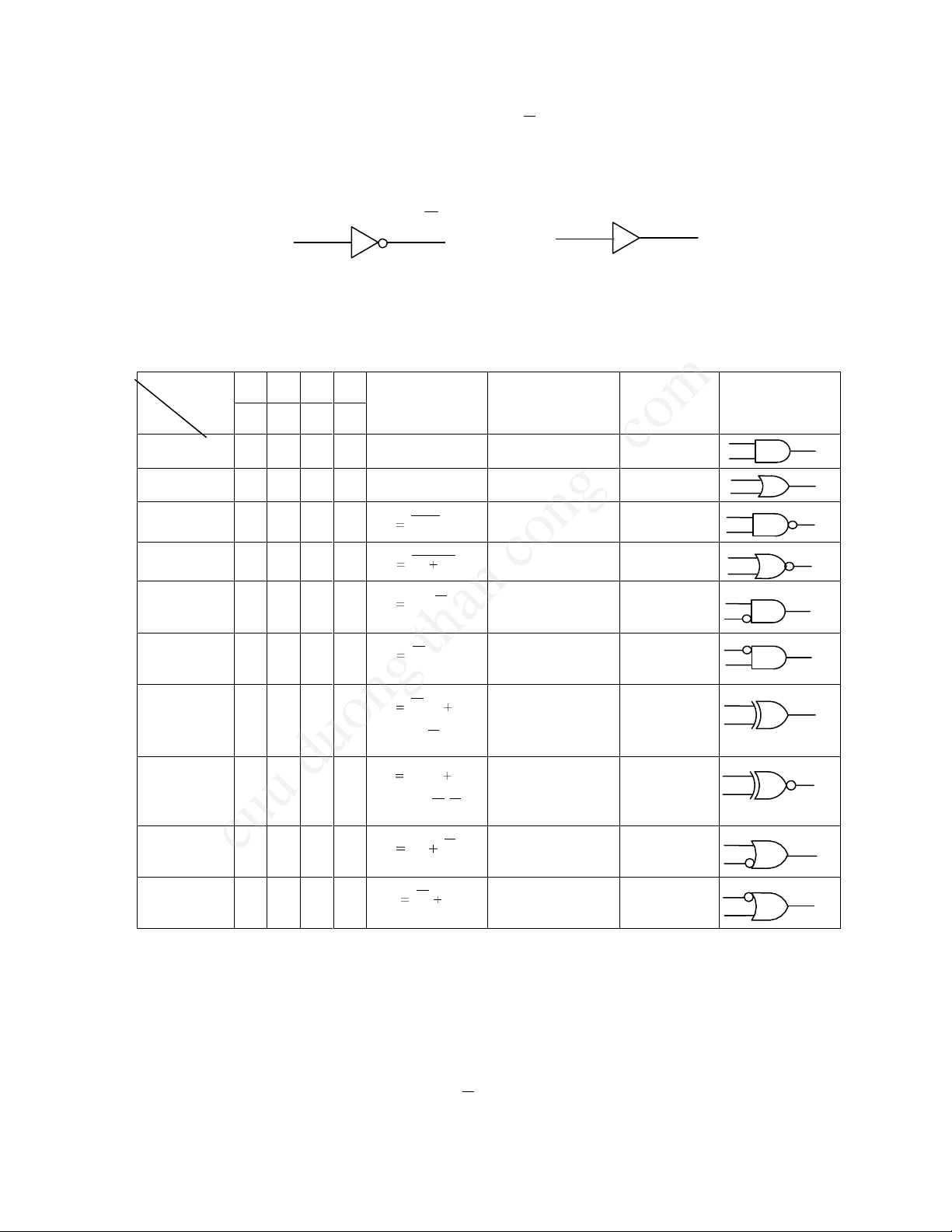VÝ dô A.B lµ phÐp an nh©n gi÷a hai biÕn logic A vµ B, mçi biÕn ®-îc gäi lµ mét thõa sè cña phÐp nh©n, th kÕt qu¶ gäi lµ tÝch sè. Cã thÓ dïng gi¶n ®å Venn trong ký thuyÕt tËp hîp (xem h×nh 3.1) ®Ó biÓu diÔn m« t¶ ba phÐp to¸n logic võa nªu. o ng du A A A+B A.B u cu a) b) c) H×nh 3.1. §å thÞ Venn m« t¶ ba phÐp tÝnh logic c¬ b¶n a. PhÐp phñ ®Þnh (NOT); b. PhÐp céng logic; c. PhÐp nh©n logic Mét tr¹ng th¸i cña ®èi t-îng nµo ®ã lu«n lu«n cã th× biÕn logic biÓu diÔn nã lu«n ë gi¸ trÞ 1, cßn khi tr¹ng th¸i cña ®èi t-îng lu«n lu«n kh«ng cã, gi¸ trÞ logic cña nã lu«n lµ 0. Ta nhËn ®-îc trong tËp hîp nµy hai h»ng sè 1 vµ 0. 3.1.2. C¸c tÝnh chÊt quan träng cña tËp hîp c¸c biÕn logic. Khi thùc hiÖn ba phÐp to¸n c¬ b¶n lªn c¸c biÕn logic, ta nhËn ®-îc mét kÕt qu¶ ®-îc gäi lµ hµm logic (hµm tr¹ng th¸i). Khi hµm logic nhËn ®-îc lµ do tõ 1 CuuDuongThanCong.com https://fb.com/tailieudientucntt
nhiÒu c¸ch t¸c ®éng cña phÐp to¸n logic kh¸c nhau ta gäi lµ chóng t-¬ng ®-¬ng nhau vµ ký hiÖu b»ng dÉu "=" gi÷a c¸c kÕt qu¶ nµy. C¸c tÝnh chÊt c¬ b¶n. * TÝnh ho¸n vÞ cña phÐp céng vµ phÐp nh©n: A + B = B + A hay A.B = B.A (3.1) * TÝnh kÕt hîp cña phÐp céng vµ phÐp nh©n (A + B) + C = A + (B + C); (A.B).C = A . (B.C) (3.2) * TÝnh ph©n phèi gi÷a phÐp céng vµ phÐp nh©n: A (B + C) = A. B + A.C (3.3) om * Hai quy t¾c cña phÐp phñ ®Þnh: .c (A )= A ; (A )=A (3.4) * Bèn quy t¾c cña phÐp céng: ng A+A=A A+ A =1 co A+0=A A+1=1 (3.5) * Bèn quy t¾c cña phÐp nh©n: an A.A=A A. A =0 th A .1 = A A.0=0 (3.6) ng * TÝnh chÊt hÊp thô: A. (A + B) = A (3.7) o du * TÝnh nhÊt qu¸n: nÕu A + B = B th× A. B = A (3.8) u * LuËt De Morgan lËp hµm phñ ®Þnh cña mét hµm: cu A+B= A .B (3.9) A.B = A B (3.10) *A+ A .B=A+B (3.11) C¸c hÖ thøc (3.1) ®Õn (3.11) cã thÓ dÔ dµng chøng minh tÝnh ®óng ®¾n cña chóng khi ta sö dông ®å thÞ Venn hoÆc sö dông c¸c c«ng t¾c tr¹ng th¸i A, B trong mét m¹ch ®iÖn víi phÐp céng lµ m¾c song song, phÐp nh©n lµ m¾c nèi tiÕp c¸c c«ng t¾c, tr¹ng th¸i nèi m¹ch cã gi¸ trÞ 1, ng¾t m¹ch cã gi¸ trÞ lµ 0. 3.1.3. C¸c hµm logic s¬ cÊp. 1. Nhãm c¸c hµm 1 biÕn Y(A) gåm 4 hµm c¬ së. 2 CuuDuongThanCong.com https://fb.com/tailieudientucntt
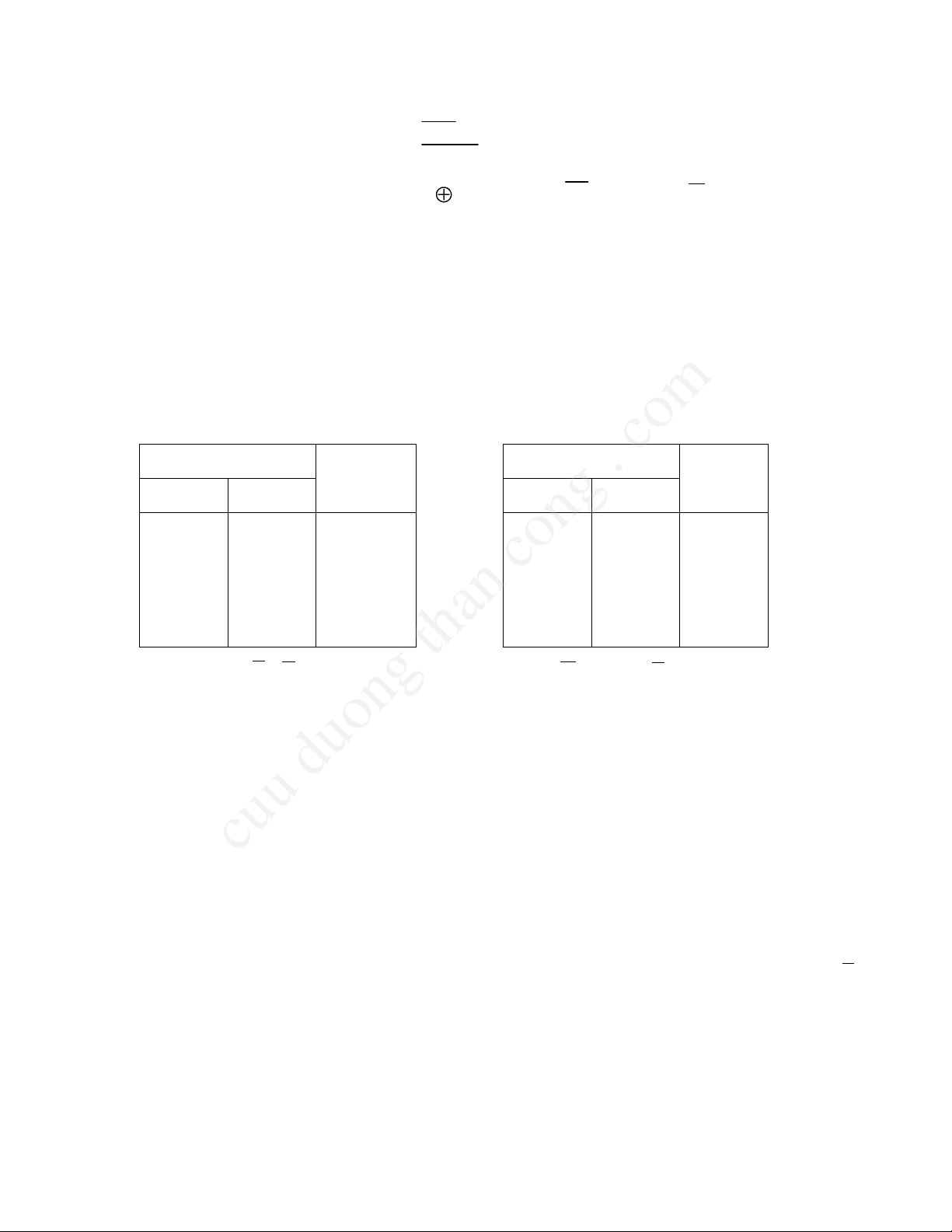
Y1 = 0 (A lu«n b»ng 0) Y0 = Y3 = A (hµm bï cña A - NOT) Y2 = 1 (A lu«n b»ng 1) Y4 = A (hµm lÆp cña A - YES) Ký hiÖu quy -íc cña Y3 vµ Y4 cho trªn h×nh 3.2. Y3 = A A Y4 = A A H×nh 3.2. Ký hiÖu quy -íc hµm NOT vµ yes 2) Nhãm c¸c hµm 2 biÕn Y (A,B) cho trªn b¶ng 3.1 B¶ng 3.1 C¸c hµm hai biÕn c¬ b¶n Tªn om BiÕn A 0 0 1 1 BiÓu thøc ®¹i Tªn gäi tiÕng Ký hiÖu quèc tÕ sè viÖt Hµm B 0 1 0 1 .c Y1 0 0 0 1 Y1 = A.B Nh©n logic AND Y2 0 1 1 1 Y2 = A+B Céng logic OR ng Y3 1 1 1 0 Y3 A .B Vµ - kh«ng co NAND Y4 1 0 0 0 Y4 A B HoÆc-kh«ng NOR an Y5 0 0 1 0 Y5 A. B CÊm B INHIBITI- ON th Y6 0 1 0 0 Y6 A .B CÊm A INHIBITI- ON ng Y7 0 1 1 0 Y7 A .B Kh«ng ®ång trÞ EX-OR o du B .A Y8 1 0 0 1 Y8 A .B §ång trÞ EX-NOR u A .B cu Y9 1 0 1 1 Y9 A B KÐo theo A IMPLI- CATION Y10 1 1 0 1 Y 10 A B KÐo theo B IMPLI- CATION HÖ hµm logic ®Çy ®ñ Tõ mét tæ hîp c¸c hµm logic s¬ cÊp nµo ®ã, ta cã thÓ x©y dùng ®-îc mét hµm logic bÊt kú. Mét nhãm c¸c hµm s¬ cÊp, tõ chóng cã thÓ x©y dùng ®-îc c¸c hµm logic kh¸c ®-îc gäi lµ mét hÖ hµm ®Çy ®ñ. Cã 4 hÖ hµm ®Çy ®ñ. a) HÖ bao gåm c¸c hµm Y0 = A ; Y1 = A.B vµ Y2 = A + B 3 CuuDuongThanCong.com https://fb.com/tailieudientucntt
b) HÖ chØ dïng hµm Y3 = A.B (NAND) c) HÖ chØ dïng hµm Y4 = A + B (NOR) d) HÖ gåm hai hµm Y7 = A B vµ Y5 = A.B (hoÆc Y6 = A .B) 3.1.4. Ph-¬ng ph¸p biÓu diÔn hµm logic vµ tèi thiÓu hµm logic 1. BiÓu diÔn hµm logic b»ng b¶ng ch©n lý. Hµm logic cã thÓ biÓu diÔn ë d¹ng mét b¶ng liÖt kª c¸c gi¸ trÞ cã thÓ cña biÕn vµ gi¸ trÞ t-¬ng øng cña hµm gäi lµ b¶ng ch©n lý (hay b¶ng tr¹ng th¸i) gièng nh- b¶ng 3.2. 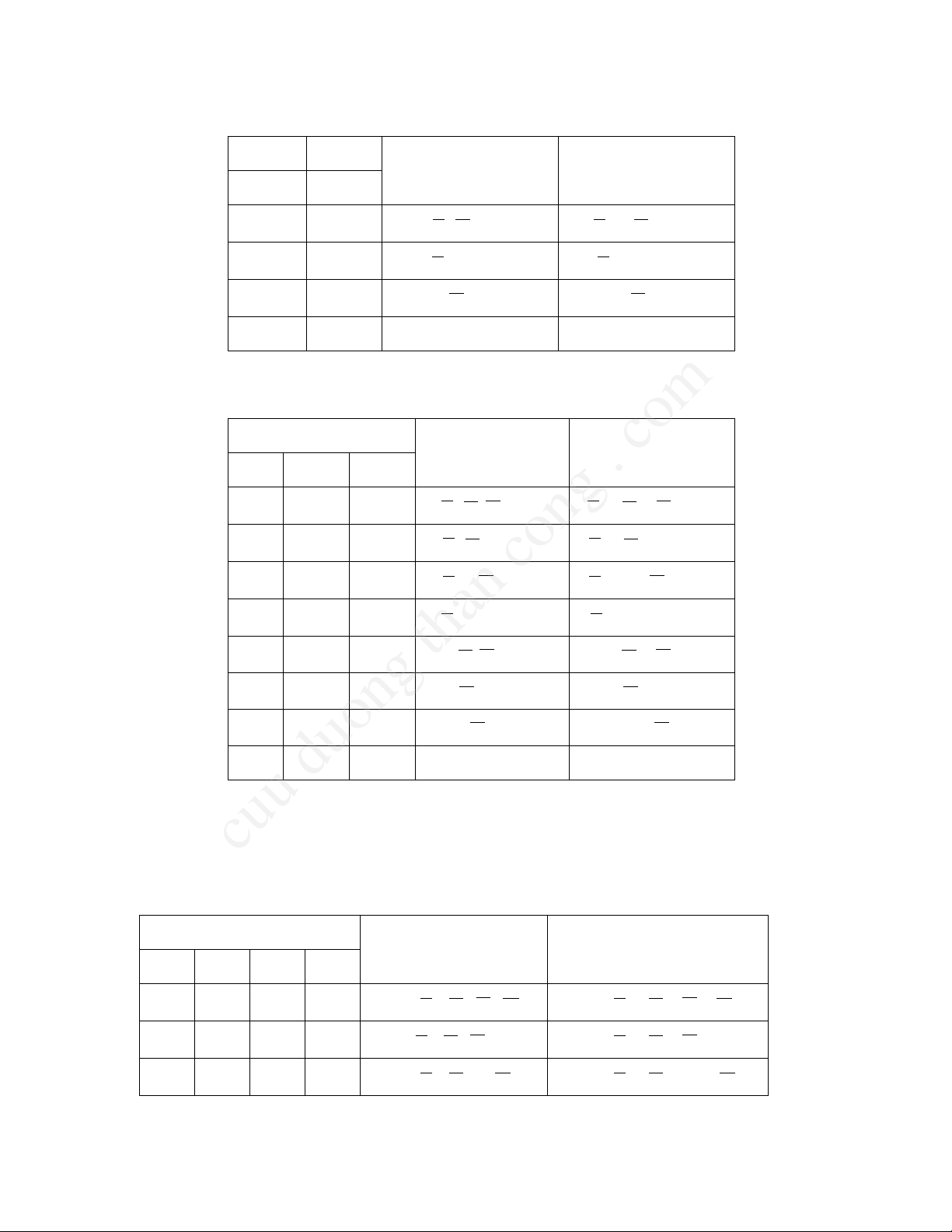Nh- vËy víi hµm hai biÕn ta cã b¶ng gåm 3 cét vµ 4 dßng, víi hµm 3 biÕn ta cã b¶ngch©n lý gåm 4 cét vµ 23 = 8 dßng (t-¬ng øng víi mäi tr¹ng th¸i tæ om hîp biÕn cã thÓ cã) B¶ng 3.2 B¶ng ch©n lý hµm 2 biÕn cu¶ hµm Y8 vµ Y7 .c BiÕn Hµm BiÕn Hµm ng A B Y8 A B Y7 0 0 1 0 0 0 co 0 1 0 0 1 1 an 1 0 0 1 0 1 th 1 1 1 1 1 0 Y8 = A . B + A.B Y7 = . B + A. B ng A 2. BiÓu diÔn hµm logic b»ng biÓu thøc. o Kh¸i niÖm vÒ MAXTERM (Mactec Mi) vµ MINTERM (Mintec mi). Ph-¬ng du ph¸p biÓu diÔn hµm logic b»ng biÓu thøc gi¶i tÝch cã hai d¹ng c¬ b¶n: u - D¹ng tæng c¸c tÝch c¸c biÕn, mçi sè h¹ng cña tæng chøa ®ñ mÆt c¸c biÕn cu ®-îc gäi lµ mét mintec ký hiÖu lµ mi. - D¹ng tÝch c¸c tæng c¸c biÕn, mçi thõa sè cña tÝch chøa ®ñ mÆt c¸c biÕn ®-îc gäi lµ 1 mactec ký hiÖu lµ Mi (chØ sè i tÝnh trong hÖ m-êi). B¶ng c¸c mi vµ Mi cña hµm 2 biÕn Y(A,B), hµm 3 biÕn Y (A,B,C) vµ hµm 4 biÕn Y (A, B, C, D) ®-îc giíi thiÖu trªn b¶ng 3.3 a, b, c. Ta cÇn chó ý, trong b¶ng 3.3 khi biÕn cã gi¸ trÞ bï (trÞ 0) ta ký hiÖu lµ A , cßn khi biÕn ë d¹ng trùc tiÕp (nhËn gi¸ trÞ 1) ta ký hiÖu t-¬ng øng lµ A. Trong cïng mét hµng cña b¶ng 3.3 a,b hay c; tæng chØ sè mi vµ Mj nµy lu«n b»ng (2k - 1) trong ®ã k lµ sè biÕn cña hµm cÆp mi vµ Mj nµy (i + j = 2k -1) ®-îc gäi lµ cïng tªn nhau, vÝ dô trong b¶ng 3.3 b cÆp m4 vµ M3 hay cÆp m6 vµ M1. B¶ng 3.3. 4 CuuDuongThanCong.com https://fb.com/tailieudientucntt
a. C¸c mi vµ Mi cña hµm hai biÕn (k =2) BiÕn Mintec Maxtec A B mi Mi 0 0 A B =m0 A + B = M3 0 1 A B = m1 A + B = M2 1 0 A B = m2 A+ B = M1 1 1 AB = m3 A + B = M0 b. C¸c mi vµ Mi cña hµm ba biÕn (k =3) om BiÕn mi Mi .c A B C ng 0 0 0 A B C co = m0 A + B + C = M7 0 0 1 A B C = m1 A + B +C = M6 0 1 0 B C = m2 + B+ C = M5 an A A 0 1 1 A BC = m3 A + B+C = M4 th 1 0 0 AB C = m4 A+ B + C = M3 ng 1 0 1 A B C = m5 A+ B +C = M2 o 1 1 0 AB C = m6 A + B+ C = M1 du 1 1 1 ABC = m7 A + B + C = M0 u cu c. B¶ng c¸c mi vµ Mi cña hµm 4 biÕn (k = 4) BiÕn Mintec mi Maxtec Mi A B C D 0 0 0 0 m0 = A .B .C .D M15 = A +B +C +D 0 0 0 1 m1 = A . B . C .D M14 = A + B + C +D 0 0 1 0 m2 = A . B .C. D M13 = A +B + C +D 5 CuuDuongThanCong.com https://fb.com/tailieudientucntt
0 0 1 1 m3 = A . B .C.D M12 = A +B + C + D 0 1 0 0 m4 = A .B. C . D M11 = A + B +C + D 0 1 0 1 m5 = A .B. C .D M10 = A + B+ C + D 0 1 1 0 m6 = A .B.C. D M9 = A + B + C +D 0 1 1 1 m7 = A .B.C.D M8 = A + B + C +D 1 0 0 0 m8 = A . B . C . D M7 = A + B + C + D 1 0 0 1 m9 = A. B . C .D M6 = A+ B + C +D 1 0 1 0 m10 = A. B .C. D M5 = A + B +C+ D om 1 0 1 1 m11 = A. B .C.D M4 = A + B + C +D .c 1 1 0 0 m12 = A.B. C . D M3 = A +B + C + D 1 1 0 1 m13 = A.B. C .D M2 = A + B + C +D ng 1 1 1 0 m14 = A.B.C. D co M1 = A + B + C+ D 1 1 1 1 m15 = A.B.C.D M0 = A + B + C + D an VÝ dô : Cho hµm th Y7 A .B B .A Khi ®ã cã thÓ viÕt d-íi d¹ng mintec: Y7 = m1 + m2 = m (1 , 2 ) ng ¸p dông c«ng thøc (3.9) ta cã: o du Y7 A .B A .B A .B .A .B A B .A B HoÆc cã thÓ viÕt d-íi d¹ng mactec: u cu Y7 M 2 .M 1 M 2 ,1 ë ®©y c¸c mintec vµ mactec tham kh¶o trong b¶ng 3.3a 6 CuuDuongThanCong.com https://fb.com/tailieudientucntt
3. BiÓu diÔn hµm logic b»ng ph-¬ng ph¸p h×nh häc (b×a c¸c n«) A AB B 0 1 C 00 01 11 10 0 A . B A. B 0 A . B .C A .B. C A.B. C A. B . C m0 m2 m0 m2 m6 m4 1 A .B AB 1 A . B .C A .B.C ABC A. B .C m1 m3 m1 m3 m7 m5 a. 2 biÕn b. 3 biÕn om AB CD 00 01 11 10 .c 00 A . B .C . D A .B. C . D A.B. C . D A. B . C . D ng m0 m4 co m12 m8 01 A . B . C .D A .B. C .D A.B. C .D A. B . C .D m1 m5 m13 m9 an 11 A . B .C.D A .B.C.D ABCD A . B .C . D th m3 m7 m15 m11 ng 10 A . B .C. D A .B.C. D A.B.C. D A. B . C .D m2 m6 m14 m10 o du c. 4 biÕn u H×nh 3.3: B×a c¸c n« cña hµm logic cu Hµm logic k biÕn ®-îc biÓu diÔn thµnh mét b¶ng cã 2k c¸c « vu«ng (mçi « t-¬ng øng víi mét mintec mi cña hµm). C¸c tæ hîp biÕn ph¶i xÕp theo thø tù lµ 2 « (2 mintec) kÒ nhau chØ ®-îc phÐp cã 1 biÕn kh¸c trÞ sè. H×nh 3.3 ®-a ra b×a c¸c n« cña c¸c hµm logic tõ 2 tíi 4 biÕn. C¸ch g¸n gi¸ trÞ cña b×a c¸c n«: « nµo øng víi gi¸ trÞ mintec m i = 1 th× g¸n gi¸ trÞ 1 vµo nã, cßn « nµo cã trÞ mi = 0 th× bá trèng, khi ®ã biÓu diÔn ®-îc b×a c¸c n« cña mét hµm logic nµo ®ã ®· cho tr-íc, nh- c¸c vÝ dô trªn h×nh 3.5 t-¬ng øng. CÇn l-u ý bªn mÐp tr¸i cña hµng vµ phÝa trªn cña cét ghi c¸c trÞ sè gi¸ trÞ cña biÕn vµ ký hiÖu biÕn t-¬ng øng theo ®óng trËt tù quy ®Þnh ®Ó tr¸nh nhÇm lÉn (nh- trªn h×nh 3.3). 7 CuuDuongThanCong.com https://fb.com/tailieudientucntt
Nh- vËy, khi lËp b×a c¸c n« cho mét hµm logic nµo ®ã ta cÇn thùc hiÖn c¸c b-íc: + LËp b×a c¸c n« øng víi sè biÕn cña hµm ®· cho, chó ý hai « kÒ nhau trong b×a ph¶i cã kho¶ng c¸ch tõ m· nhÞ ph©n lµ tèi thiÓu (kh¸c nhau chØ cã mét gi¸ trÞ nhÞ ph©n). + Sau khi ®· ®ñ c¸c « trèng (®óng qui t¾c) c¸c mintec m i cã mÆt trong biÓu thøc cña hµm sÏ ®-îc ®iÒn 1 vµo vÞ trÝ cña « t-¬ng øng trong b×a, nghÜa lµ trong biÓu thøc cña hµm cã bao nhiªu sè h¹ng mi sÏ cã ®ñ bÊy nhiªu « cã trÞ 1 trong b×a c¸c n«. om A A AB B 0 1 B 0 1 C 00 01 11 10 .c 0 1 0 1 0 1 ng 1 1 1 1 co 1 1 1 1 Y7= A B + A B Y8= AB+ A B F= A BC+ A B C+ AB C + ABC a) b) c) an AB th CD 00 01 11 10 00 1 Y= + B C D+ A B D ng A B C D A C 01 1 1 + ABCD + ABC D + A BC D o du 11 1 10 1 1 u cu H×nh 3.5. C¸ch biÓu diÔn hµm logÝc b»ng b×a c¸c n« Chó ý: Khi lËp b×a c¸c n«, ta ph¶i chó ý ®Õn trËt tù c¸c con sè trong c¸ch biÓu diÔn c«ng thøc vµ trong b×a c¸c n« ph¶i nh- nhau. 3.1.5. Rót gän (tèi thiÓu ho¸) hµm logic. Bµi to¸n kü thuËt liªn quan tíi hµm logic rÊt ®a d¹ng. VÊn ®Ò cÇn quan t©m lµ lµm c¸ch nµo ®Ó dÔ dµng gi¶i bµi to¸n nhê c¸c m¹ch ®iÖn tö cã sè phÇn tö logic s¬ cÊp Ýt nhÊt. Bëi v×, nh÷ng m¹ch cµng Ýt linh kiÖn cµng dÔ ®¹t tíi tèi -u, cã ®é tin cËy vµ ®é chuÈn ho¸ cao, linh kiÖn s½n cã trªn thÞ tr-êng. V× vËy, ta cÇn ph¶i rót gän hµm logic. Cã hai c¸ch rót gän hµm logic th«ng dông lµ rót gän b»ng gi¶i tÝch vµ rót gän b»ng b×a c¸c n«. 8 CuuDuongThanCong.com https://fb.com/tailieudientucntt
1. Ph-¬ng ph¸p rót gän b»ng gi¶i tÝch dùa trªn c¸c tÝnh chÊt cña ®¹i sè logic, c¸c hÖ thøc ®· biÕt (3.1) ®Õn (3.11); khi sè biÕn ligic kh«ng nhiÒu biÓu thøc gi¶i tÝch cña hµm ®-îc biÕn ®æi trùc tiÕp. VÝ dô 1: Rót gän hµm sau: Y(A, B, C, D)= A B + C+ A C D+ B C D = A B + C+ C ( A D+ BD) ¸p dông tÝnh chÊt A+ A B = A+ B cã: Y(A, B, C, D)= A B + C.1+ C ( A D+ BD) A B + C+ ( A D+ BD) = A B + C.1+ D( A + B) om dïng tÝnh chÊt (3.9) ( A + B)= AB vµ tÝnh chÊt A+ A .B = A + B .c Y= A B + C+ D A B = C+ D + A B ViÖc tèi thiÓu hµm logic b»ng ph-¬ng ph¸p gi¶i tÝch cho ta kÕt qu¶ tèi thiÓu ng tèt nhÊt. co 2. Ph-¬ng ph¸p rót gän b»ng b×a c¸c n« sö dông quy t¾c vßng « kÒ nhau (qui t¾c c¸c n«) an C¸c « cã trÞ 1 n»m kÒ nhau, ta cã thÓ vßng chóng l¹i thµnh 1 « lín, ®¹i diÖn cho 1 sè h¹ng rót gän ®i mét sè biÕn". Khi sö dông quy t¾c c¸c n« cÇn l-u ý mÊy th tr-êng hîp sau: ng - Sè c¸c « vßng l¹i ph¶i b»ng 2n (n lµ sè nguyªn 0,1,2,3...) - Hai hay nhiÒu « n»m ë 2 mÐp cña b×a tÝnh theo hµng hay theo cét còng o ®-îc coi lµ kÒ nhau. du - Mét hoÆc vµi « cã trÞ 1 cã thÓ tham gia vßng nhiÒu lÇn vµo c¸c nhãm kh¸c nhau (nhãm ®éc lËp, kh«ng chøa nhau). u cu - Kh«ng ®-îc thùc hiÖn vßng c¸c «, mµ sau khi vßng « lín cã ®-îc, l¹i chøa nhau hay chøa tÊt c¶ c¸c « con ®· ®-îc vßng tõ tr-íc ®ã. §Ó lµm râ quy t¾c ta nªu vµi vÝ dô minh ho¹. VÝ dô 1: H·y rót gän hµm Y(A,B,C)= ABC + A BC+ A B C+ AB C Hµm Y cã b×a c¸c n« cho trªn h×nh 3.5 gåm 4 « cã trÞ 1 øng víi c¸c mintec m3,m5,m6 vµ m7. Thùc hiÖn vßng m3 víi m7, m6 víi m7 vµ m5 víi m7 ta ®-îc 3 « míi ký hiÖu t-¬ng øng lµ X1, X2 vµ X3 c¸c « nµy cã gi¸ trÞ: 9 CuuDuongThanCong.com https://fb.com/tailieudientucntt
X1 = m3 + m7 = BC AB X2 = m6 + m7 = AB C 00 01 11 10 X3 = m5 + m7 = AC 0 1 m6 kÕt qu¶ ta ®-îc hµm Y ®· rót gän: Y = X1 + X2 + X3 1 1 m3 1 m7 1 m5 = BC + AB + AC H×nh 3.5 Rót gän hµm theo vÝ dô 1 VÝ dô 2: Rót gän hµm Y (A,B,C,D) cho trªn b×a c¸c n« (h×nh 3.6). BiÓu thøc ®Çy ®ñ cña hµm G cã d¹ng: Y = m (0,1,2,4,6,7,8,9,10,11,12,14), gåm 12 sè h¹ng cã ®ñ mÆt c¸c biÕn om ABCD. Ta cã thÓ thùc hiÖn vßng « nh- sau: .c ¤ lín X1 gåm cã m0 + m4 + m12 + m8 + m2 + m6 + m14 + m10 KÕt qu¶ lµ X1 = D ng AB 00 01 11 10 ¤ lín X2 = m0 + m1 + m8 + m9CD = co B C 00 1m0 1 m4 1m12 1 m8 ¤ lín X3 = m8 + m9 + m10 + m11 = an AB 01 1 m1 1 m9 th ¤ lín X4 = m6 + m7 = A BC 11 1 m7 1m11 Hµm G sau khi rót gän cã d¹ng: ng 10 1 m2 1 m6 1m14 1m10 G = X1 + X2 + X3 + X4 = D + B C + o AB + A BC H×nh 3.6 Rót gän hµm theo vÝ dô 2 du Trong c¸c vÝ dô trªn, l-u ý r»ng trong mét « lín sau khi ®· vßng c¸c « nhá, c¸c biÕn logic nµo cã gi¸ trÞ thay ®æi th× sÏ kh«ng cã mÆt trong biÓu thøc thu gän u cña c¸c Xi n÷a. cu Khi tèi gi¶n b»ng b×a c¸c n«, møc ®é tèi gi¶n hµm logic phô thuéc vµo viÖc ghÐp c¸c « lín. Do ®ã, tèi gi¶n b»ng b×a c¸c n« cã thÓ cho kÕt qu¶ rót gän ch-a tèi -u. 3.2. c¸c cæng logic c¬ b¶n 3.2.1. Cæng thùc hiÖn phÐp c«ng logic (cæng or) BiÓu thøc logic thùc hiÖn chøc n¨ng hoÆc: YOR = A + B (3.12) 10 CuuDuongThanCong.com https://fb.com/tailieudientucntt
B¶ng tr¹ng th¸i, biÓu thøc hµm, c¸c ký hiÖu quy -íc cña cæng OR hai ®Çu vµo cho trªn h×nh 3.7a,b. BiÕn vµo Hµm ra A B YOR = A + B 0 0 0 A Y 0 1 1 B 1 0 1 1 1 1 om a) b) H×nh 3.7: Cæng hoÆc (OR) a) B¶ng ch©n lý; b) ký hiÖu .c Ta nhËn xÐt lµ: YOR = 1 khi cã bÊt kú ®Çu vµo nµo cña nã cã trÞ 1 ng YOR = 0 chØ khi tÊt c¶ c¸c ®Çu vµo cã trÞ 0 co YOR = 1 khi tÊt c¶ c¸c ®Çu vµo cã trÞ 1 tøc lµ cã tÝnh chÊt A + B +... + N = 1 + 1 +... + 1 = 1 an VÝ dô mét vµi d¹ng m¹ch ®iÖn tö sè thùc hiÖn hµm OR ®-îc cho trªn h×nh th 3.8a,b. Khi A = 1 hoÆc B = 1 hoÆc A = B = 1 (t-¬ng øng víi møc ®iÖn ¸p lín h¬n + 3V) ta nhËn ®-îc Y = 1 (øng víi møc ®iÖn ¸p lín h¬n + 2,4V). Cßn khi A = B = 0 ng (møc ®iÖn ¸p gÇn 0V) cæng ra ë møc nhá h¬n 0,7V (Y =0). +5V o A Y=A+B du 3V A T1 B T2 0V B Y=A+B u cu R RA RB -12V H×nh 3.8: VÝ dô vÒ m¹ch ®iÖn tö sè thùc hiÖn cæng OR ë m¹ch h×nh 3.8b, T1 vµ T2 lµ 2 tranzitor t¹i hai cæng ra cña 2 vi m¹ch sè, chÕ t¹o theo c«ng nghÖ logic ghÐp emit¬ (logic kh«ng b·o hoµ - ECL). Khi ®Êu hai ®Çu ra cña chóng víi nhau ta ®-îc Y = A + B. Khi sö dông lo¹i ECL cã thÓ chØ dïng mét IC víi hai cæng vµo A vµ B vµ 2 cæng ra trong ®ã cã mét cæng ra thùc hiÖn hµm Y (cæng ra cßn l¹i thùc hiÖn hµm Y ). 11 CuuDuongThanCong.com https://fb.com/tailieudientucntt
3.2.2. Cæng thùc hiÖn phÐp nh©n logic (cæng and) BiÓu thøc thùc hiÖn chøc n¨ng vµ: YAND = A.B (3.13) B¶ng tr¹ng th¸i, ký hiÖu quy -íc cña cæng AND 2 cæng vµo cho trªn h×nh 3.9. Ta cã nhËn xÐt lµ: YAND = 1 chØ khi tÊt c¶ c¸c cæng vµo cã gi¸ trÞ logic 1 YAND = 0 khi cã Ýt nhÊt mét cæng vµo cã gi¸ trÞ 0 om BiÕn vµo Hµm ra A B YAND = A . B .c 0 0 0 A YAND = A.B 0 1 0 ng A 1 0 0 co 1 1 1 b. an a. th H×nh 3.9: Cæng AND; a. B¶ng ch©n ký cña cæng AND, b Ký hiÖu M¹ch ®iÖn tö sè thùc hiÖn hµm YAND ng +12V +12V A o du R A B u Y=A.B Y=A.B cu B a. b. H×nh 3.10. C¸c m¹ch ®iÖn tö sè thùc hiÖn hµm AND H×nh 3.10. ®-a ra m¹ch ®iÖn tö sè thùc hiÖn hµm AND. Khi cã mét ®Çu vµo nµo ®ã ë møc ®iÖn ¸p thÊp, ®i«t t-¬ng øng víi ®Çu vµo nµy sÏ dÉn ®iÖn, khi ®ã ®iÖn ¸p ë cæng ra (khi kh«ng t¶i) sÏ ë møc thÊp b»ng gi¸ trÞ ®iÖn ¸p thuËn r¬i trªn ®i«t (0,7V víi lo¹i ®i«t Si). Cßn khi tÊt c¶ c¸c cæng vµo ®Òu ë møc ®iÖn ¸p cao c¸c ®ièt ®Òu kh«ng dÉn ®iÖn lµm gi¶m ¸p trªn ®iÖn trë R nhá, Y ®Çu ra ë møc ®iÖn ¸p cao. 12 CuuDuongThanCong.com https://fb.com/tailieudientucntt
Chó ý r»ng khi m¾c Rt¶i ë t¹i cöa ra, R vµ Rt¶i h×nh thµnh mét bé chia ¸p ®iÖn trë khi A = B = 1, khi ®ã cÇn ®¶m b¶o ®iÒu kiÖn cña møc ra cao nhá nhÊt (vÝ dô lµ 2V). VÝ dô tÝnh cho R = 3,9k E0 12 V U ra min R tai R tai 2V R R tai 3 ,9 K R tai hay 12V. Rt¶i = 2V (3,9K + Rt¶i) Suy ra ®iÒu kiÖn ®èi víi t¶i m¾c vµo cæng lµ Rt¶i min = 780 Còng nh- cæng OR, viÖc thùc hiÖn b»ng c¸c m¹ch ®iÖn tö sè cæng AND kh«ng ®-îc thuËn lîi v× lý do c«ng nghÖ. om .c 3.2.3. Cæng thùc hiÖn hµm ®¶o (phñ ®Þnh logic - not) 1. Nguyªn lý cæng thùc hiÖn hµm ®¶o. ng YNOT = co A (3.14) B¶ng ch©n lý, ký hiÖu quy -íc cña cæng NOT (®-îc cho trªn h×nh 3.11) BiÕn Hµm an A A th A A 0 1 ng 1 0 o du a. b. H×nh 3.11: Cæng ®¶o; a. B¶ng ch©n lý; b. Ký hiÖu u Nh- vËy cæng NOT lu«n lu«n chØ cã E2= +12V cu mét ®Çu vµo vµ mét ®Çu ra víi gi¸ trÞ biÕn vµo vµ hµm ra lu«n lµ gi¸ trÞ ®¶o cña nhau. R3 1K Khi ghÐp liªn tiÕp hai cæng NOT ta sÏ nhËn Y ®-îc hµm lÆp (hµm Y4 trong h×nh 3.2), trÞ A R1 hµm ra lu«n b»ng trÞ biÕn vµo. 1,5K T 2. M¹ch sè thùc hiÖn cæng NOT R2 18K (h×nh 3.12) E1= -12V H×nh 3.12 S¬ ®å m¹ch ®iÖn cæng ®¶o 13 CuuDuongThanCong.com https://fb.com/tailieudientucntt
ë h×nh 3.12. T lµm viÖc ë chÕ ®é ®ãng ng¾t, khi U A ë møc thÊp th× T ng¾t (kh«ng dÉn dßng ®iÖn), ®iÖn ¸p cæng ra UY ë møc cao. Khi UA chuyÓn lªn møc cao ( A = 1) th× T nèi m¹ch ë chÕ ®é b·o hoµ, chuyÓn UY vÒ møc thÊp (Y = 0) 3.3. c¸c cæng logic kh¸c 3.3.1. Cæng thùc hiÖn hµm logic hoÆc ®¶o (cæng NOR) 1. Nguyªn lý cæng thùc hiÖn hµm hoÆc ®¶o. BiÓu thøc thùc hiÖn cøc n¨ng cæng hoÆc ®¶o om Y NOR A B (3.15) .c B¶ng ch©n lý, ký hiÖu quy -íc cña mét cæng NOR cã hai ®Çu vµo (h×nh 3.13a,b,c) ng BiÕn vµo Hµm ra co A YNOR = A+B B A B YNOR = A +B an 0 0 1 b. th 0 1 0 A ng 1 0 0 YNOR = A+B B o 1 1 0 du c. a. u H×nh 3.13: Cæng hoÆc ®¶o (NOR) a. B¶ng ch©n lý; b. ký hiÖu; c. Ký hiÖu t-¬ng ®-¬ng OR - NOT cu Ta cã nhËn xÐt lµ: + §Çu ra cæng NOR sÏ lªn møc cao (YNOR = 1) khi tÊt c¶ c¸c ®Çu vµo cña nã ë møc thÊp. + YNOR = 0 (®Çu ra ë møc thÊp) khi cã Ýt nhÊt 1 ®Çu vµo cña nã ë møc cao. + Cæng NOR lµ sù kÕt hîp liªn tiÕp cæng OR vµ cæng NOT. 2. M¹ch ®iÖn thùc hiÖn hµm NOR M¹ch h×nh 3.14 lµ sù ghÐp nèi tiÕp cæng OR h×nh 3.8a vµ cæng NOT h×nh 3.12a theo ký hiÖu t-¬ng ®-¬ng h×nh 3.13c võa nªu trªn. 14 CuuDuongThanCong.com https://fb.com/tailieudientucntt
E2= +12V R3 1K Y= A B A R1 B 1,5K R2 18K E1= -12V om H×nh 3.14 Cæng NOR kÕt hîp tõ hai cæng OR vµ NOT .c 3.3.2. Cæng logic thùc hiÖn hµm vµ - ®¶o (cæng NAND) ng 1. Nguyªn lý cæng thùc hiÖn hµm vµ ®¶o. BiÓu thøc thùc hiÖn chøc n¨ng cæng vµ - ®¶o co Y NAND A .B (3.16) an B¶ng ch©n lý, ký hiÖu quy -íc cña mét cæng NAND hai ®Çu vµo (h×nh 3.15a,b), ký hiÖu t-¬ng ®-¬ng cña cæng NAND (h×nh 3.15c) th ng BiÕn vµo Hµm ra A Y NAND A .B B o A B Y NAND A .B du 0 0 1 b. u 0 1 1 A cu Y NAND A .B B 1 0 1 c. 1 1 0 a. H×nh 3.15: Cæng vµ ®¶o a. B¶ng ch©n lý cña cæng AND; b. ký hiÖu Ta cã c¸c nhËn xÐt sau: - YNAND = 0 chØ khi tÊt c¶ c¸c ®Çu vµo cña cæng NAND ë møc cao (A = B =1) - YNAND =1 khi cã Ýt nhÊt mét ®Çu vµo cña cæng NAND ë møc thÊp. 15 CuuDuongThanCong.com https://fb.com/tailieudientucntt
- Cã thÓ xem cæng NAND nh- lµ ghÐp nèi tiÕp mét cæng AND víi mét cæng NOT (xem h×nh ký hiÖu t-¬ng ®-¬ng h×nh 3.15c) 2. M¹ch ®iÖn tö sè thùc hiÖn c¸c cæng NAND M¹ch ®iÖn h×nh 3.16 m« t¶ cÊu tróc cæng NAND DTL nhê c¸ch ghÐp nèi tiÕp cæng AND h×nh 3.10 víi mét cæng NOT h×nh 3.12a thùc hiÖn theo cÊu tróc m« t¶ bëi h×nh 3.15c. E2= +12V R3 1K Y=A.B om A R1 .c B 1,5K R2 18K ng E1= -12V co H×nh 3.16: S¬ ®å m¹ch ®iÖn cæng NAND kÕt hîp liªn tiÕp cæng AND vµ NOT an 3.3.3. Cæng kh«ng ®ång trÞ (EX - NOR) th Cæng kh«ng ®ång trÞ thùc hiÖn hµm logic kh¸c dÊu, kh«ng ®ång (cïng) trÞ ng sè. BiÓu thøc logic cã d¹ng: Y = A + B = A.B + A.B (3.17) o du A A.B BiÕn vµo Hµm ra u cu Y A B Y=A+B 0 0 0 B A.B 0 1 1 1 0 1 A Y A Y + 1 1 0 B B a. b. H×nh 3.17: Cæng kh«ng ®ång trÞ a. B¶ng ch©n lý ; b. S¬ ®å ®iÖn vµ kÝ hiÖu. 16 CuuDuongThanCong.com https://fb.com/tailieudientucntt
B¶ng ch©n lý cña hµm ®-îc giíi thiÖu trªn h×nh 3.17a S¬ ®å m¹ch ®iÖn hµm nµy ®-îc vÏ trªn h×nh 3.17b. Tõ b¶ng ch©n lý h×nh 3.17a ta thÊy nã gÇn gièng b¶ng ch©n lý cña cæng hoÆc, chØ kh¸c lµ ë ®©y khi hai cæng vµo cïng 1 th× ®Çu ra b»ng 0. Cæng EX-NOR sÏ cã ®Çu ra b»ng 1 khi c¸c tr¹ng th¸i ®Çu vµo cã sè lÎ c¸c sè 1. V× vËy cã thÓ xem lµ mét m¹ch ph¸t hiÖn c¸c bÝt lÎ. Cæng nµy cßn cã tªn gäi kh¸c lµ cæng kh¸c dÊu; khi hai ®Çu vµo cã gi¸ trÞ gièng nhau ®Çu ra cã gi¸ trÞ lµ 0 cßn khi ®Çu vµo cã gi¸ trÞ kh¸c nhau ®Çu ra cã gi¸ trÞ lµ 1. Tõ biÓu thøc (3.17) ta cã thÓ x©y dùng cæng nµy tõ c¸c cæng vµ, hoÆc, kh«ng nh- trªn h×nh 3.17b. om 3.3.3. Cæng ®ång trÞ (EX - OR) Cæng ®ång trÞ thùc hiÖn hµm logic cïng trÞ sè. BiÓu thøc logic cã d¹ng: .c Y = A + B = A.B + A.B (3.18) ng B¶ng ch©n lý cña hµm ®-îc giíi thiÖu trªn h×nh 3.18a. S¬ ®å m¹ch ®iÖn hµm nµy ®-îc vÏ trªn h×nh 3.18b. co Theo b¶ng ch©n lý h×nh 3.18a, ta thÊy khi hai cæng vµo cïng trÞ sè (1 hoÆc 0) th× ®Çu ra b»ng 1, cßn khi cæng vµo kh«ng cïng trÞ sè ®Çu ra b»ng 0. Nh- vËy cæng an EX-OR sÏ cã ®Çu ra b»ng 1 khi c¸c tr¹ng th¸i ®Çu vµo cã sè ch½n c¸c sè 1. V× vËy cã thÓ xem lµ mét m¹ch ph¸t hiÖn c¸c bÝt ch½n. th Tõ biÓu thøc (3.18) ta cã thÓ x©y dùng cæng nµy tõ c¸c cæng vµ, hoÆc, kh«ng ng nh- trªn h×nh 3.18b. A A.B BiÕn vµo Hµm ra o B du A B Y=A+B Y u 0 0 1 cu 0 1 0 A.B 1 0 0 A Y A Y + 1 1 1 B B a. b. H×nh 3.18: Cæng ®ång trÞ a. B¶ng ch©n lý; b. S¬ ®å ®iÖn vµ kÝ hiÖu. 17 CuuDuongThanCong.com https://fb.com/tailieudientucntt
3.4 Ph-¬ng ph¸p thiÕt kÕ s¬ ®å m¹ch logic ThiÕt kÕ m¹ch logÝc cã thÓ ®-îc thùc hiÖ b»ng nhiÒu c¸ch. phæ biÕn lµ b»ng hai c¸ch: 1 - tõ s¬ ®å m¹ch cã tiÕp ®iÓm chuyÓn ®æi thµnh m¹ch kh«ng tiÕp ®iÓm b»ng c¸c cæng logic; 2 – x©y dùng l-u ®å thuËt tãan, viÕt hµm logic vµ thiÕt kÕ m¹ch theo hµm logic. chóng ta sÏ tiÕn hµnh thiÕt kÕ theo hai c¸ch nµy. 3.4.1.ThiÕt kÕ chuyÓn ®æi tõ m¹ch tiÕp ®iÓm thµnh m¹ch kh«ng tiÕp ®iÓm. H×nh 34.1 giíi thiÖu mét sè s¬ ®å m¹ch vÝ dô cña viÖc chuyÓn ®æi s¬ ®å m¹ch tiÕp ®iÓm sang s¬ ®å m¹ch logic om .c ng a) co b) an th c) ng d) e) o H×nh 34.1 ChuyÓn ®æi s¬ ®å m¹ch tiÕp ®iÓm sang du m¹ch kh«ng tiÕp ®iÓm u H×nh 34.1 a m¹ch tiÕp ®iÓm cã nót nhÊn vµ tiÕp ®iÓm tù duy tr× m¾c song cu song nªn khi chuyÓn sang s¬ ®å logic dïng cæng hoÆc. ®-êng håi tiÕp b»ng ®i«t ®-a vÒ lµ m¹ch tù duy tr× khi ®Çu ra lªn møc cao. H×nh 34.1 c cã nót nhÊn th-êng kÝn m¾c nèi tiÕp víi nót nhÊn th-êng hë vµ tiÕp ®iÓm tù duy tr×. M¹ch logic ®-îc thùc hiÖn b»ng cæng vµ víi hai nót nhÊn kÝn vµ hë trung thùc nh- m¹ch tiÕp ®iÓm (h×nh 34.1 d). M¹ch logic còng cã thÓ ®-îc thùc hiÖn b»ng hai nót nhÊn th-êng hë nh- h×nh 34.1 e. M¹ch logic cã thÓ ®-îc thùc hiÖn b»ng mét sè phÇn tö kh¸c vÝ dô dïng trig¬ ch¼ng h¹n. C¸c ®iÖn trë ®-îc m¾c tíi c¸c cængvµo cña IC lµ cÇn thiÕt v× c¸c lo¹i IC sè kh«ng ®-îc ®Ó hë c¸c ch©n vµo, khi ®ã IC rÊt nhËy víi nhiÔu. 18 CuuDuongThanCong.com https://fb.com/tailieudientucntt
H×nh 34.2, 34.3, 34.4 giíi thiÖu mét sè s¬ ®å vÝ dô chuyÓn ®æi tõ m¹ch tiÕp ®iÓm sang m¹ch kh«ng tiÕp ®iÓm. R1 RA K§1 RA RB RC RB R1 RC R1 Rth th L§ L§ R1 Rth R2 om R2 K§2 .c H×nh 34.2ChuyÓn ®æi m¹ch tiÕp ®iÓm thµnh m¹ch logic ng MT T MT MN N MN T co N T an T th ng H×nh 34.3 ChuyÓn ®æi ®¶o chiÒu b»ng tiÕp ®iÓm thµnh m¹ch logic o du u M K M D Rth cu K§2 K D V1 V3 K2 K Rth R K§ K1 K K Rth K§1 Rth K2 § V3 K1 H×nh 34.4 ChuyÓn ®æi m¹ch khëi ®éng ®æi nèi sao tam gi¸c b»ng tiÕp ®iÓm thµnh m¹ch logic 19 CuuDuongThanCong.com https://fb.com/tailieudientucntt
3.4.2. ThiÕt kÕ s¬ ®å logic tõ l-u ®å thuËt to¸n Khi ®· cã m¹ch tiÕp ®iÓm, chuyÓn ®æi thµnh m¹ch kh«ng tiÕp ®iÓm thùc hiÖn b»ng c¸c m¹ch mÉu ®iÓn h×nh vÝ dônh÷ng m¹ch trªn h×nh 34.1 1 1. Th-êng biÓu diÔn d-íi XuÊt ph¸t tõ yªu cÇu tù d¹ng: ®éng ho¸ V¨n b¶n L-u ®å s¬ ®å chøc n¨ng om 2 TiÕn hµnh x©y dùng: 2. C«ng viÖc nµy bao gåm thÓ hiÖn .c S¬ ®å khèi c¸c chøc n¨ng chñ yÕu vµ nhËn L-u ®å thuËt to¸n d¹ng ®èi víi mçi chøc n¨ng c¸c ®Çu vµo/ra cÇn thiÕt lËp logic c¶u mçi ng BiÓu ®å thêi gian biÓu ®å tr¹ng th¸i khèi co an 3 3. ¸p dông c¸c ph-¬ng ph¸p sau ®Ëy: T×m kiÕm m¹ch tæ hîp th B¶ng ch©n lÝ logic thùc hiÖn chøc B×a C¸cn« ng n¨ng mçi khèi hoÆc Sö dông catal« vµ b¶ng tra cøu c¸c tÝnh to¸n vÒ logic ®èi m¹ch tÝch hîp o víi mçi khèi du u 4 4. Theo chøc n¨ng, lùa chän m¹ch cu BiÓu diÔn chuÈn ho¸ 4 tÝch hîp vµ kÕt qu¶ ¸p dông c¸c lo¹i s¬ ®å trªn ph-¬ng ph¸p gi¶i, thiÕt lËp c¸c s¬ ®å kh¸c nhau. H×nh 34.5 Tr×nh tù thiÕt kÕ m¹ch logic Khi thiÕt kÕ m¹ch logic cho c¸c bµi to¸n c«ng nghÖ th-êng ®-îc tiÕn hµnh theo thiÕt kÕ 4 lo¹i s¬ ®å sau: ThiÕt kÕ s¬ ®å m¹ch giao diÖn ®Çu vµo. BiÓu diÔn s¬ ®å m¹ch logic. 20 CuuDuongThanCong.com https://fb.com/tailieudientucntt