2
'3E
(0k

( )
-
:
−
←→ −
⇒

( )
( )
:
- - : : ::
−
−−
←→− =
−
−
'
⇒
( )
( )
( )
": ":
-" - :
:
−
−
←→ = −
−
 *
( ) ( )
( )
( )
": ":
. - -" - :
:
−
−
= ←→ = −
−
' '
gVk•\•uh
36+>
A!!$P/+,$1(,:0)!#,FA)k
?]^p


n[
−
≥
<
<
4;*!j$.]^>F($%*A/;*!j$/Ad
,"7F1(k
?]-^p
-"
-
-n[
−
≥
<
<

⇒
?]-^f
b-"
]-^
0"5)ik
( )
{ }
( ) ( )
Z% Z% Z'
<
...
"
- -
? - ? - : ? - : :
+∞ +∞ −
=−∞ =
= = = + +
∑ ∑

( ) ( )
'
...
" "
: :
− −
= + + +
;$
( )
"
:
−
<
,LR&$,7(,:+/A,0&)($8(;960;+
/$A>0+1D9@$1)(0+),7(,?,0&)($8(;960;+/$A>0+
1d,6$*:k
( )
{ }
( )
-
"
"
:
? - :
:
− −
= =
−
 *k 
( )
( )
( )
-"
"
"
:
- :
:
−−
←→ = −
−
(
)
:
" "
aN : :
−
> ⇔ >
!"#'3'
'3G
;,O$8,:+,@j@A)6$*:k
( )
-
:
-
:
:
−
←→ =
−
−
U616E+;;;9D=8kB
0A!
(
)
h :
dRA,0"K,:/A,L!
(
)
? -
0(0+),7(
R;"0&X)7F1(d,(0k
( ) ( )
-
? - h : : :
d
−
=π
∫
'
>F/A"7FA)(0)%?R;,%*AY!,:0)V($8
(
)
h
>AR0
)0 ;( ,01 "0 
L!?]-^RY)(0+),7(,:+:;,97(,19d,71(,;,,7FA)
9@$1)((((6$k
! -07 
(
)
h :
   #?":
##T
PCGBU656
0
( ) ( )( )
:
h : : :
=
− −
'
L!Qg%h
-6
.+,?(
(
)
h
d,"7F1(k
( ) ( )
: :
h : : :
−
= +
− −
'
:R8)R;"0&Xk
( )
-
:
-
:
←→
−
H$*:k ?]-^f]b
-
i%
-
^]-^
! .07 
(
)
h :
 G%>
0"5)iR;"0&:k
( ) ( )
( ) ( )
( )
-
-
h : ? - : ? : ? : ? : ? :
( )
+∞ − − − −
=
== = + + + +
∑
< '
<
< '
U0"0;$9+,?(
(
)
h :
,A,0&)($8($0j/$P*,7A,
6P"7F1(),:5?]-^ (? / A  6 0; ($8 , A 9 # :
r
-

2
'3N
PCGBU616
0
( ) ( )( )
:
h : : :
=
− −
'
L!Qg%h
-6

( ) ( )( )
: :
h : : : : :
= =
− −
− +
'
'
2 E
",7(d,"7F1(k
( )
h : : : : :
− − − −
= + + + +
'
2  E2
H$*:k?][^f[e?]^fe?]^f+e?]%^f$e?]*^f,+@000
! 2A7ICU#H 0 N
PCGBU6>6
0
( ) ( )( )
:
h : : :
=
− −
'
L!Qg%h
-6
(0k
( ) ( )( )
: : :
h : : :
: : : :
−
− −
= = =
− − − + − +
' '
' 2 E 2 E
⇒
(
)
( )
: : h : :
− − −
− + =
'
2 E
⇒
( ) ( ) ( )
h : : h : : h : :
− − −
− + =
' '
2 E
T;"0&X)7F1(>;97F),:L,:+g"&*,?(;,@FA
,:0)!#,FA)hd,"7F1(k
?]-^b+?]-b^i,?]-b^f
δ
]-b^
⇒
?]-^f+?]-b^b,?]-b^i
δ
]-b^
F  "# $%   "#$ k?]-b^f[e?]-b^f[
*>A0(0+),7(,:+,,L!"7F1(k
?][^f[e?]^fe?]^f+e?]%^f$e?]*^f,+@000
! 3KV= 0 M=
( ) ( )
( )
Re
-b
-
: h :
? - ' : h :
−
=
∑
;$
/A ( 71( R ( !0 , ,Lk
( )
( )
( )
Re
- -
: :
: :
' : h : : : : h :
− −
==
= −
;$
/ A( 71( R (9 ,L k
( )
( )
( )
( )
33
- -
: :
3
: :
' : h : : : : h :
3 :
Re !
−
− −
=−
=
= −
−
<
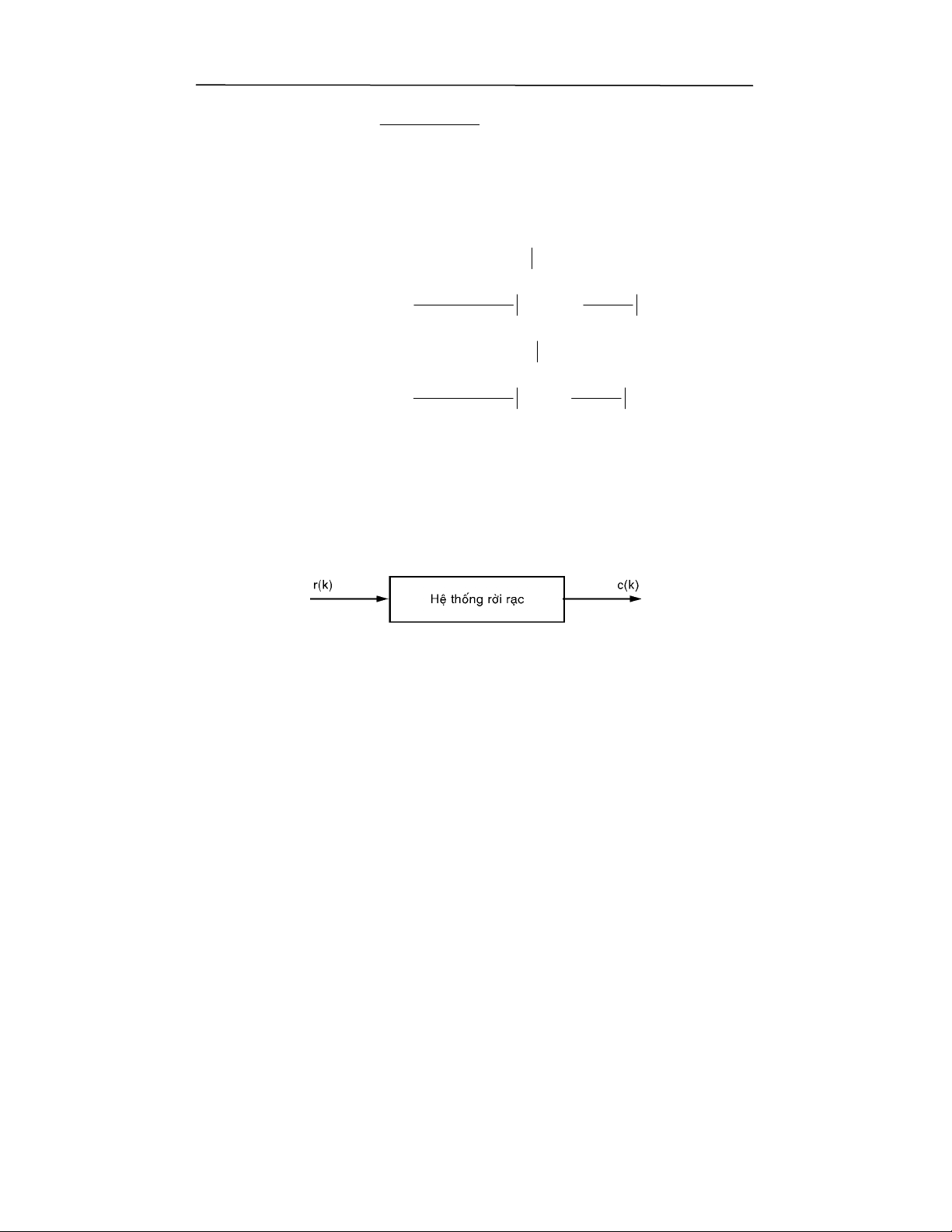
!"#'3'
'3
PCGBU6E6
0
( ) ( )( )
:
h : : :
=
− −
'
L!Qg%h
-6
D9@$1)(0+),7(,K)@7d,"7F1(k
( ) ( ) ( )
- -
: :
? - ' : h : ' : h :
Re Re
− −
= =
= +
'
=Ak
( ) ( ) ( )
- -
: :
' : h : : : h :
Re
− −
=
=
= −
'
'
'
p
( ) ( )( )
-
:
:
: : : :
−
=
−− −
'
'' p
( )
-
-
:
:
:
=
= −
−
'
'
( ) ( ) ( )
- -
: :
' : h : : : h :
Re
− −
=
=
= −
p
( ) ( )( )
-:
:
: : : :
−
=
−− −
' p
( )
-
-
:
:
:
=
=
−
'
U0"0k?]-^fb
-
i%
-
1#!(3 
U6>65D?<??B
S$   ) 7P , ?   $ >A 0 >A ,?   $ : ($ 8  , 0; ) :FA : 1(
"7F1(!0+,8RY)97F),:L69+k
(
)
(
)
(
)
(
)
- - - -
−
+ + + − + + + + =
p
(
)
(
)
(
)
(
)
6 6
1 . - 6 1 . - 6 1 . - 1 . -
−
+ + + − + + + +
gGGh
,:0)"0
≥
6d) 01 /A R (( $8  ,0 ;) :FA : 1(
T;"0&:>;97F),:LgGGh,"7F1(k
( ) ( ) ( ) ( )
: : : : : : :
−−
+ + + + =
p
( ) ( ) ( ) ( )
6 6
6
1 : a : 1 : a : 1 :a : a :
−−
+ + + +
⇔
( )
: : : :
−−
+ + + +
p
( )
6 6
6 6
1 : 1 : 1 : 1 a :
−−
= + + + + +
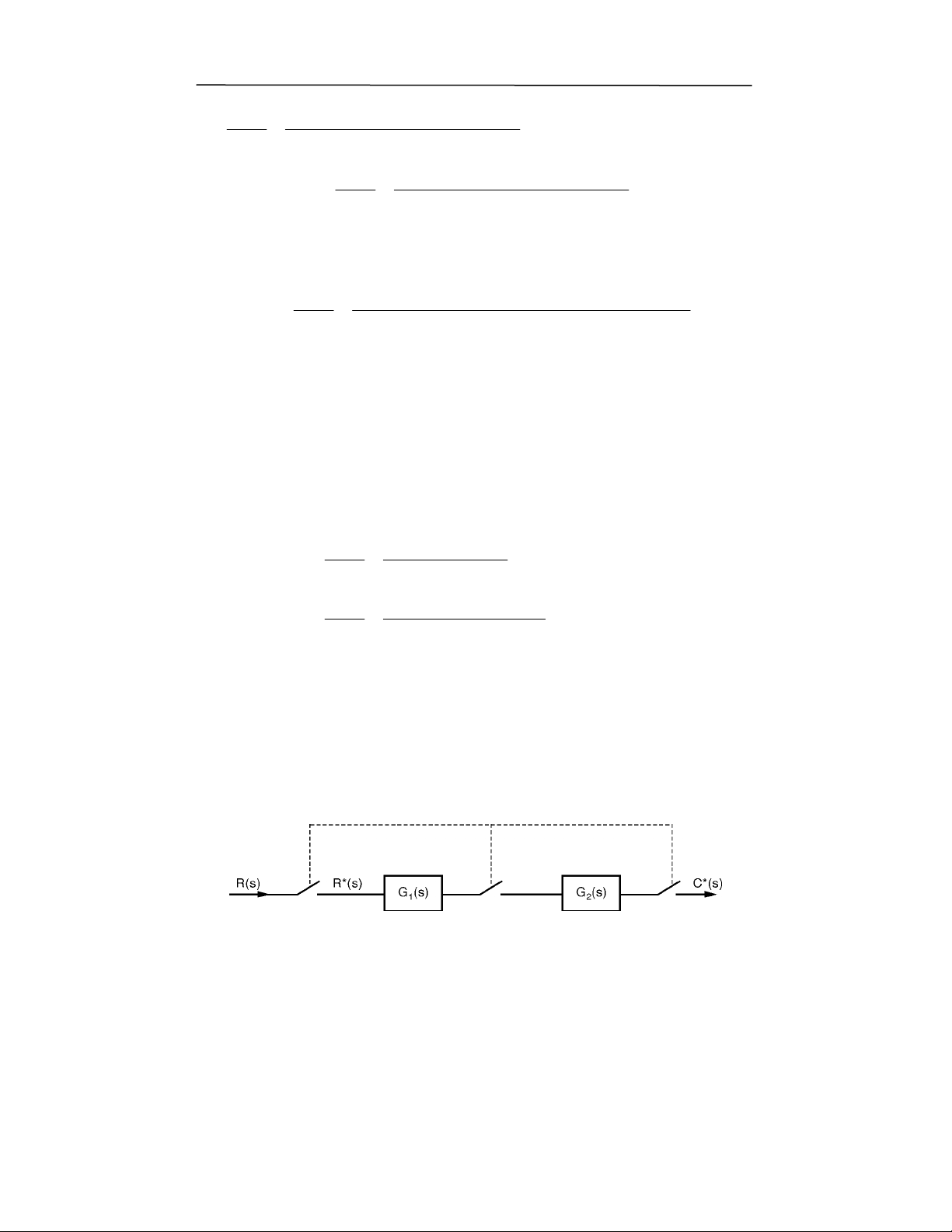
2
'2<
⇔
( )
( )
6 6
6 6
1 : 1 : 1 : 1
:
a :
: : :
−−
−−
+ + + +
=+ + + +
K,k
( ) ( )
( )
6 6
6 6
1 : 1 : 1 : 1
:
P : a :
: : :
−−
−−
+ + + +
= = + + + +
gGNh
(
)
P :
"7 F1( )01 / A A! ,:$* # ($8  , 0;) :F A: 1(
A!,:$*#gGNh(0,&R;"0&,7F)"7F)>#@1)k
( ) ( )
( )
6 6 6
6 6
: 1 1 : 1 : 1 :
:
P : a : : : :
( )
− − − − + −
−
− − + −
−
+ + + +
= = + + + +
gGh
((R&$@j,:+0A,0A,7F)"7F)$d,:0)
,71(,;A!,:$*#@1),7"7F1(678@$1)#$F
PCGBU636
 0 , 0;) : FA :1( !0+ , 8RF 8 97F ) ,:L 6 9 + k
(
)
(
)
(
)
(
)
(
)
(
)
- - - - . - . -
+ + + − + + = + +
' ' 2 ' '
L ! A! ,:$* # ($8  , 0; )
-6
T ; "0&  X  > ; 9 7F ) ,: L 6  9 + ! 0+ ,8 ,0 ;)d ,
"7F1(k
( ) ( ) ( ) ( ) ( ) ( )
: : : : : : : : a : a :
+ − + = +
' '
' 2 '
⇒

( ) ( )
( )
: :
P : a : : : :
+
= =
+ − +
'
'
'
' 2
⇔

( ) ( )
( )
(
)
: : :
P : a :
: : :
− −
− − −
+
= = + − +
'
'
'
' 2
 !"#$%""&'%
 , + !>A 0 , 0;) / + , $1( ( (% +$ / ;*! j$d % +$ ) 7P
@7 P / $ g> A R0 "# $ % & 6 0;h ,  "7F1 (  ,0 ;) " # $ % & :F A : 1(
TA  ,0  " K, : / A ,L!  A! ,:$* #  :FA : 1( , 0R ;  :,7A6F"0#
% 0; (0 ( (% +$ /; *! j$ s ,!0 ,6 0; 6F" 0#, 7F A) )K9 6$ "+ *k
-6+0  #0%G
+,85
;-31-96D