6
E
? ?
c ? ? ?
R
( )
( )
( )
sin ( ) (sin ( ) )
sin ( ) (sin ( ) )
>
=
− <
ω ω >
=
− ω ω <
'
'
' '
' '
<
<
<
<
_/AA!/8d+T
p<
!
sin ( ) sin ( )
π
= ω ω ω
π
∫
'' '
<
3
!
( cos ( )) (cos( ))
π
−
= − ω ω
π
∫
'' '
<
3
!
cos ( )
(cos( ) )
π
ω
= ω −
π
<
'
'
3
!
= − =
π π
' '
3 N
*k
C=
π
N
,\
;611
7 F) ,71 A !R ( , :+
A!R ( R ($P )/ A A! /8 +
#
p<
c ? ?
R
( )
sin ( )
=
= ω
(0k
!
sin ( )sin ( ) ( )
π
= ω ω ω
π
∫
'
<
!
cos( )
( cos( ) ) ( )
π
+ ω
= − ω + ω
π
∫
'
<
3
' '
3 '
!
cos( ) sin ( )
( s in ( ) )
π
ω ω
= − ω +
π
'
<
3 ' N
!( )= π =
π
3 3
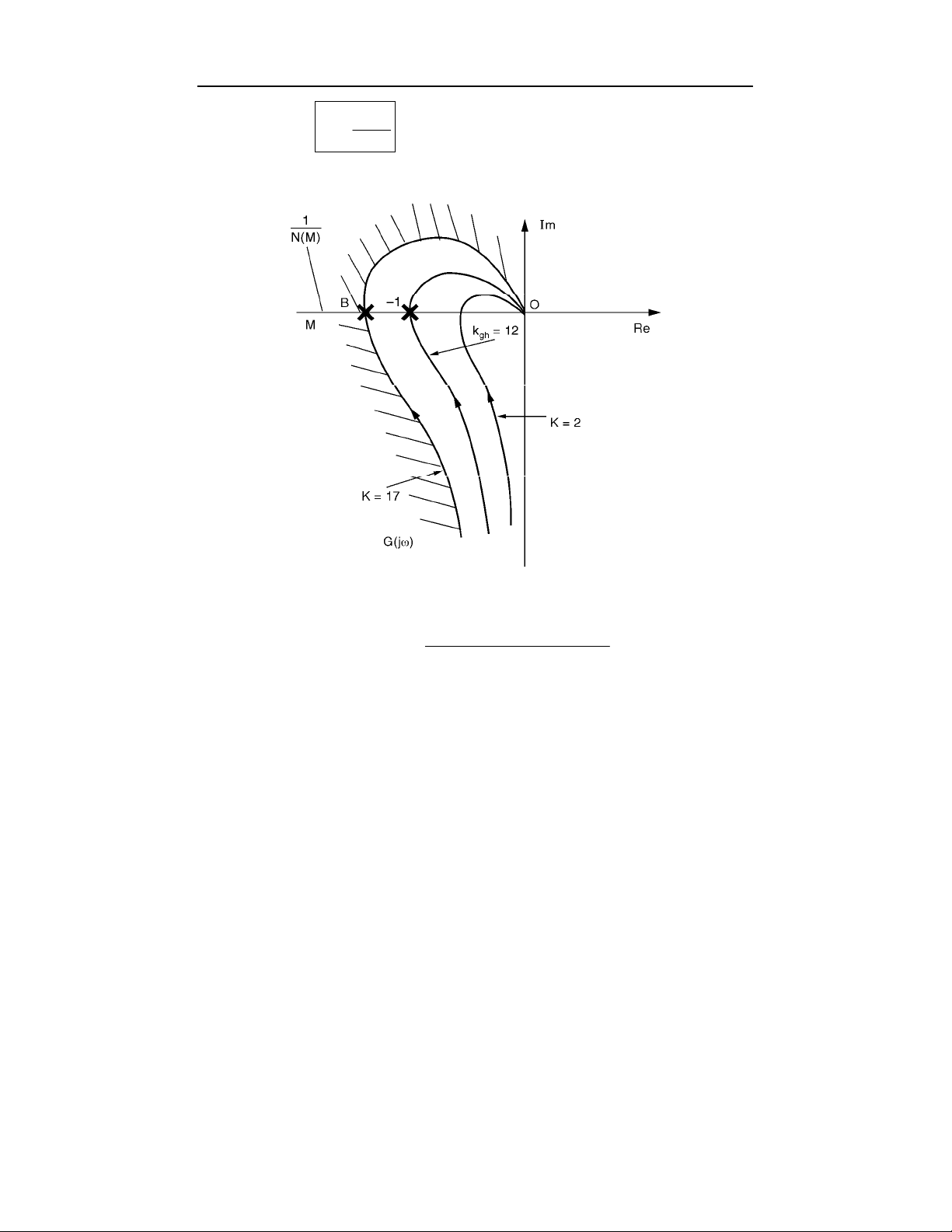
45
G
*k
C=
'
3
Y)
A !,: $* # F8( $8 9 # ,$* ; ,? !0 , 9 , $*;
+,;9
&
P d ; d
d d d
( ) ( )
( , )( , )
ω ω =
ω + ω + ω
< 2 <
. 7F ),:L " K(,? ($ 8 9# ,$* ;,? / + ,$1( (0 6 0;
$;("1RY)
! ' ' ' ' &
! ' ' ' ' &
( ) ( , )( , )
( ) , ,
= + + +
= + + +
'
< 2 <
< <2 < E
60; % $;( "1 )F 1 " 7F1( Q ( "5 , 0 , +$ ($ &
$ :[ ,\( 0 R ( R /Ak
& &
, ,∆ = − =
⇒
=
'
< E < <2 < '
7FA)(0)*O$6,(0R,:7FA)F19%($"7F1(>P
F8LG0"&!($8"0#,5Zeg=h>F"7FA)(0)*O$6,
($8 9# ,$*; ,?
P d
( )
ω
(0
&
p G %* $ / A " &! T 1
" &! T, 0#, 1 @0 "0 )% 0+ ) 0 & "5 >L ", 0 ( #$ , f) ($8
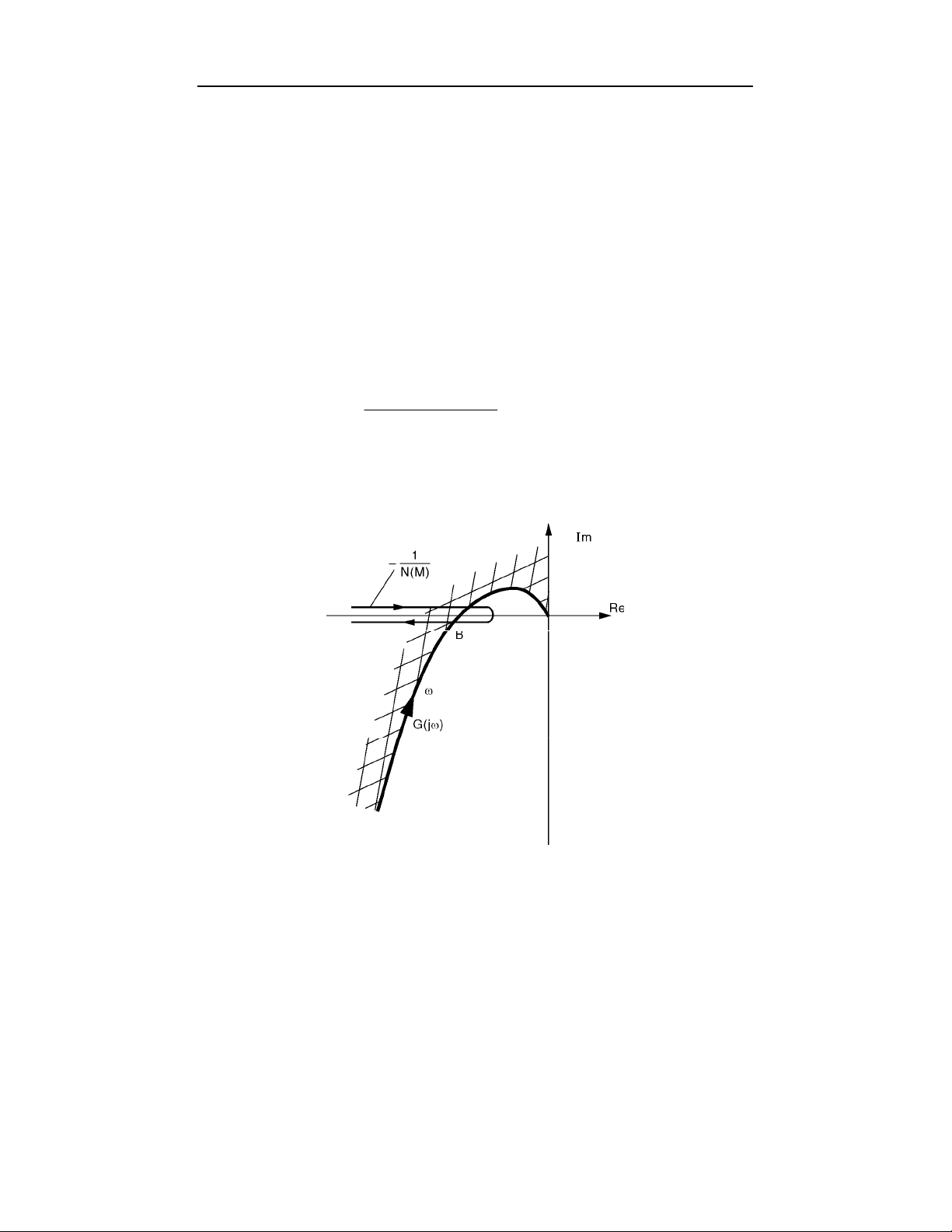
6
N
R + "0 , 0"K( , ?Z eg= h( $8% +$ 9 , $*; d( $*& "0 )
,7A>$A)0&"5g)1(601(R+,:
P d
( )
ω
h6)>$A)%0+)0&
"5($89#,$*;,?
( )
G j
ω
)7 F1( /1 d (; "0 @ 0 "0 ) /A 0&
"5 d ;$ ",0 ( #$, f) ($ 8R + "0 ,0 "K (,? Z e g=h
($8%+$9,$*;d($*&,7A>$A)%0+)0&"56)0&"5
($89#,$*;,?
P d
( )
ω
:0) ,:7FA) F19 p 'd "K( ,? Ze ($8 %+$ 9 ,$*;
Y!0A,0AF8>$A)0&"5($8
P d
( )
ω
d
≤ ω < +∞
<
d % ;, /$
9,$*;/A0&"5F8,:1),(+RY)k
Vg,hp<
Y)
9 , $* ;" K( ,? : F/ >5, :? %0+ ) ,:j >F 9 #
,$*;,?k
&
P '
' ' '
( )
( . )( )
=+ +
< ' '
.,$*;,?LG(0
_
p<dl
p<l
&
pE
.7F),:L(+RY)"#$0A)#"$)k
(
)
P d C
( )
+ ω =
<
g'2h
+,
;;
8RY)97F)99"0#,5:7F(,+,L!
−π
ω
Z/A,#60;
@ 0" 0 ) ,1 T
45
. .,
−π −π
π
+ ω + ω = π
< ' '
'
6$*:
−π
ω
pd2N6(
Z
oK,
_
!
=
l?,7Ag'2h,(0k
! f@
! f@+$ , ; ,
⇒
= =
'
< < '2
.7F),:Lg'2h>;,(0>?@$1($1,&%
Up<g:F/'>5,:?h
&
P d
. ( )
ω + =
π
3
<
1"&!T,(0k
&
P d
. ( )
−π
ω + =
π
3
<
*
,( , )
− + =
π
3 E
< <E3 <
6$*:
p<d'GN
&
,: 0 ),: 7FA )F 19 :F/ F8 >5 ,: ?%0 +) ,: jd @0 "0 )
0& "5 , 1 " &! T ( 0 R + "0
! f @+$
l,#60;
, sec
−
−π
ω =
2N
;$)7P)$*+9#,$*;,?d,*%+$9,$*;/A:F/'d
>5 ,:? U p< ,( 0 (; "0 @0 "0 ) ,1 T/ Ak
6
( ) , sin ,
=
< 'GN 2N
(;"0 ,71@0"0 )
9)
W6365'_A=
s; 9Q ^R; ,(7 9 ,$* ; A 0"0# )) i > F> (9 +" 01
,$ *; ,? ,7A )% $( / A( 0+) ( $1( 0 $ O$ 8( 0> ( 9 + ,?(
=0j "01 @j "; 97F) ,:L > 9+ ,$*; ,? ,7F) 7)
"F ) 8 F .7 F) 9 9 A*d %0 +) 1 ( ;( 0 ) # ,$* ;
,? d (0 ?( /F 1 /A ,1 0 : /F A ) 8 ( ? Q ( ( 0 R ; , ( 7 R ( 9
,$*; A0 ;$ R8 ,+ 9 ,$*; (0 ,& ,$*; ,? 0 ,7A)
"01 * (0 ,& Q;9 Q^ RY) (( "01 ,$*; ,? 6P (7)
!7)@$1)($80O$>?@$16$k
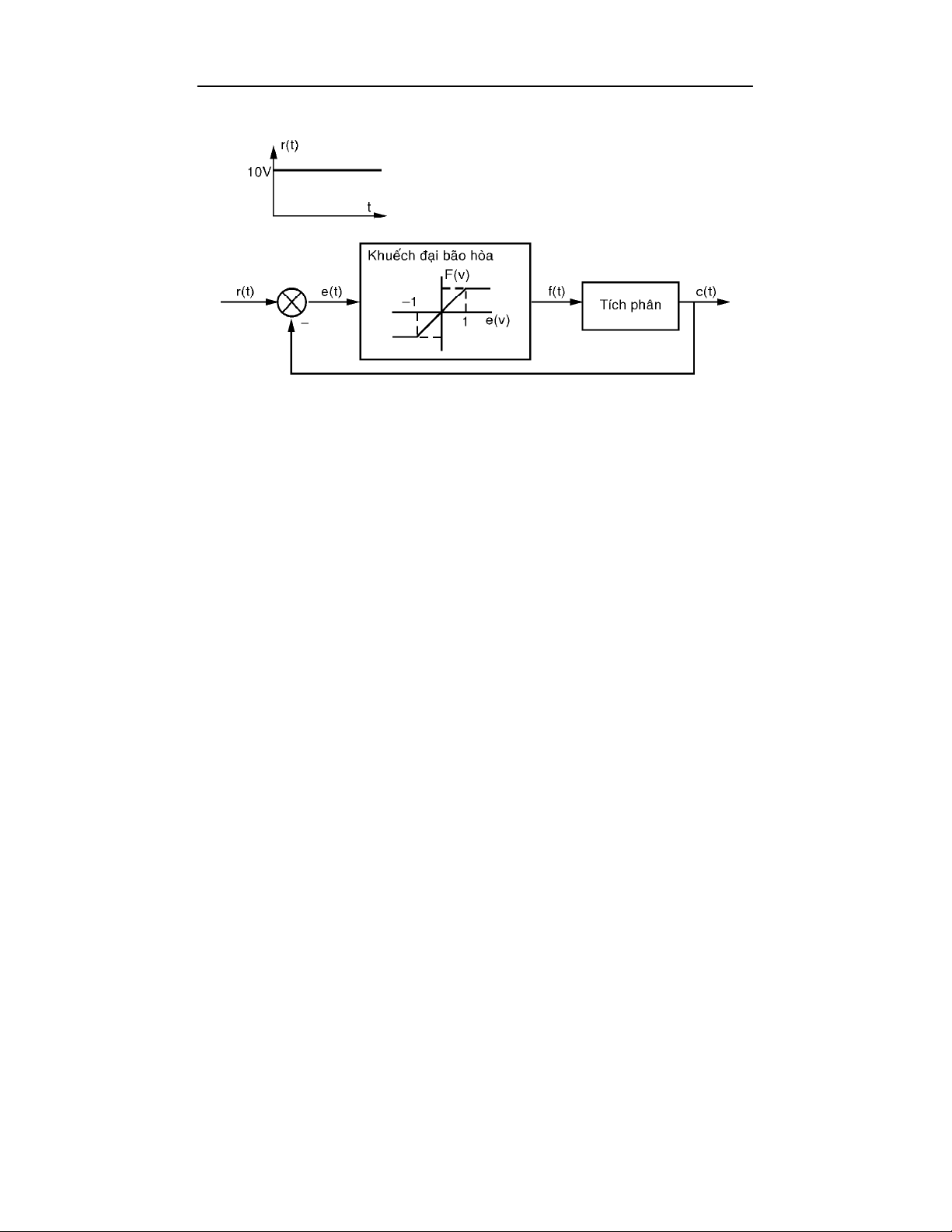
6
3<
W6361PCGBGB
+,;-<
;-231=
L < ! 01 ! 0 , " #$ % & 0# ,; 9 "F ) 8
( 7R 0 , ?(9 + > AR0 % $; ("1 R P00 A 0 / F1R 0 % $;(
" 1/A 2 ,: 0) ! 0 , , #!" 9> A0
1
±
0; > F( (" 9>A0
/F F dR0 % $; ("1 RP 00A 0 A, 0A : 0P: A)(0 >$ A)
0 1, "0 ) ,$* ; ,? 9 + R ,( $8 R0 % $;( "1 = 0j >$A ) 01 ,
"0 ) ,$ *; ,? A* ( 0 ,& Q ! Q , ! 0 , ( ( "0 ( / 9 R Y)
97F)99,$*;,?0,7A)"01"&(0"7F1("97),0&)
F 19( $8 ,0 ;)
0 ;>F >$ A) % 0+ )RP 00A d" `) ,7 (0 1,"0 ) , 0; )
/A
.
( ) ( ) ( )
= −
g'Eh
`
( ) ( )
=
2
g'Gh
`
( ) ( )
=
∫
g'Nh
H$0;,O$,:LRP00Ad97F),:Lg'Eh>Ag'Nh>j(0
),:5$*+g'Gh,*"0&,A
mg,hp2%g,hu g'h
mg,hpZ2%g,htZ g<h
8 67 8 " #$ % " #$ /A %0 +)> A "# $ >A 0 A ! ;( < d R &$
,7 ( "#$ : ,: 0) >$A )0 1, "0 )R P0 0A
( )
sat
c t
"7F1((0RF8
![Đề cương chi tiết học phần Lý thuyết điều khiển tự động [chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2021/20210417/lovebychance01/135x160/5501618651902.jpg)
![Trắc nghiệm Điều khiển tự động [mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250924/kimphuong1001/135x160/96131758686268.jpg)
