2
'N'
Z*
: d1
= + g" #$ % k 1
)
+ =
' '
>A097F),:L"K(
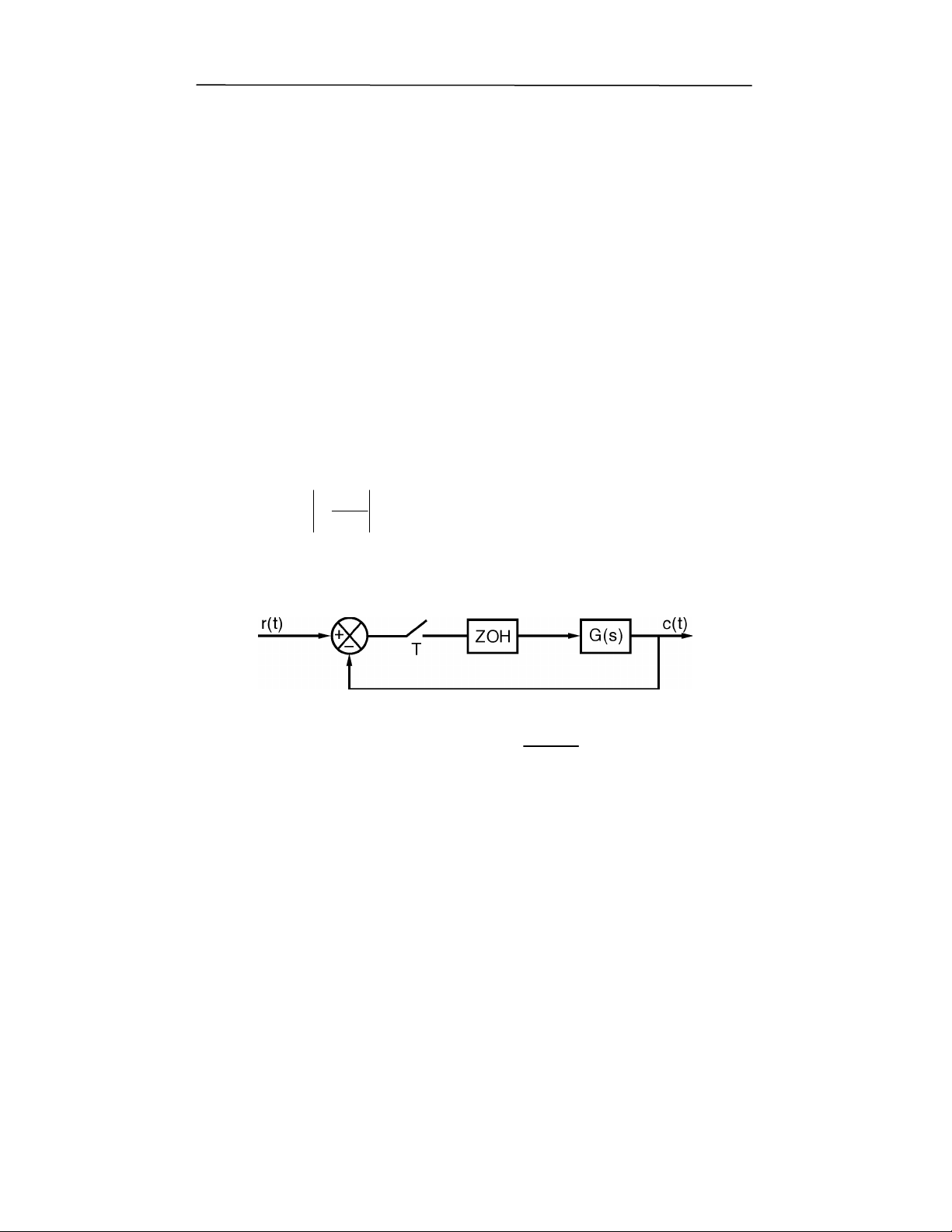
,?gNEhd(+RY)9#,71(>A9#806P,L!"7F1()0"&!
>F"7FA),:0A"F>5>A),:5&


,XWM
0( Q$ ;,9 ,( $8 O $*P" 10)  ! 6 0;, 1(71 (97 (
3
d
"7F1(Q("5RF8
6
d d d
d
3 : 3 3
= =
≠
θ = ° + − − −
∑ ∑
N< gNh
U1)L01(($8(0+),7(,:+/A
θ
~
pN<
0
zg
∑
)0(,7A((\:0";(71(3
d
h
rg
∑
)0(,7A(((71((0A/1";(71(3
d
h gN'h
,X5260&)(() !/AY)60;%&,*"0&,7A<→z∞
,X55M  60; %$ ;( " 1@0 1(, 0O$ *P " 10 )  !60; (0
, & Q( "5 ,7 A" #$ %  R+ "0
( )
( )
C :
&_ :
=
gNh
PCGBV6>6 0    ,0 ;) " # $ % & :F A :1 ( (0 6 F "0# % 0;  7 L
>Pd,:0)"0
ZA!,:$*#%+$/+,$1(
2
2
( )
( )
=
+
&
P ' ' '
Z$%*A/;*!j$
"
, sec
=
<
 P*> P S H ( $8  ,0 ;) ,: + %  &,*"0&,7A<";+∞0
?&

0
-6. 7F ),: L "K (,? ( $8  (0 6F "0 #% 0; 7 ,: + /A
P :
( )
+ =
<
4!+3'3'
'N
,:0)"0

{
}
( ) ( ) ( )
5N;
P : P ' P '
=
2
2
( )
−
−
=
+
"'
&
' ' '

'
2
2
( )
( )
−
= −
+
& : ' '
 : : :
&:: :
. , ,
,
[( , ) ( , )]
( ) ( )
− − −
−
− − + + − −
=
− −
< 2 < 2 < 2
' < 2
< 2 < 2
2
⇒
:
P : & : :
, ,
( )
( )( , )
+
=− −
< <' < <N
< E<G
⇒
.7F),:L"K(,?/A
:
&: :
, ,
( )( , )
+
+ =
− −
< <' < <N
<
< E<G gN3h
Z((71(k
3
=
d
3
,=
'
< E<G
gp'h
Z(\:0k
:
,= −
< N2G
g6ph
Z 0( ,1 0R F8 , !(   >A ,: $1( ,71 (
6
( ) ( )+ π + π
α = = = π
− −
' '
'
]f[^
Z 0 " &! )7 P,  ! ( >F  ,:$1 (, 71(
( , ) ( , ) ,
< E<G < N2G
' 3E3
'
 :.
N! 6
−+ − −
= = =
− −
∑ ∑
Z & !, (   9 /A )  ! ($8 9 7F ),: L
&
:
=
<

(0
gN3h
⇒
: : : :
&: :
( )( , ) , ,
, , , ,
− − − +
= − = −
+ +
'
< E<G E<G < E<G
< <' < <N < <' < <N

⇒
 & : :
: :
, ,
, ,
− +
= − +
'
E<G < E<G
< <' < <N

: : : :
:
( , )( , , ) ( , , )( , )
( , , )
− + − − +
= − +
'
'
' E<G < <' < <N E<G < E<G < <'
< <' < <N
 : :
:
, , ,
( , , )
+ −
= − +
'
'
< <' < <E < <3'
< <' < <N
2
'N3
⇒

&
:
=
<
⇔
:
:
,
,
= −
=
'
' 2<E
< G'
8) !,:+"#$,$0 (SH
⇒
(0"&!,( 9
Z0"&!($8SH>F"7FA),:0A"F>5
gN3h ⇔
: : & :
( )( , ) ( , , )
− − + + =
< E<G < <' < <N <
⇔: & : &( , , ) ( , , )
+ − + + =
'
< <' E<G < <N < E<G <
U $A) , +$ ($& V 0$, Z$ :[ ,\! F8: 0 )
0&R;
l
:
l
+
=
−
d,"7F1(
l l
& &
l l
( , , ) ( , , )
+ +
+ − + + =
− −
'
< <' E<G < <N < E<G <
⇔&l & l &, ( , , ) ( , , )
+ − + − =
'
< < < GNE < <E '3 < << <
 #$ % " &   ,0; )0 & "5 /A
&
&
&
, ,
, ,
>
− >
− >
<
< GNE < <E <
'3 < << <
⇔
&
&
&
,
>
<
<
<
' N
<G
' N
,
⇒
=

&
*

&
,
=
' N
>A097F),:L"K(,?d,"7F1(
: :,
− + =
'
3N2 <
 ⇔
: d
, ,
= ±
< 2G3' < NNG
 * )0 " &!( $8 S H> F >0A ),: 0A "F >5 /A
< 2G3' < NNG
, ,
= ±
: d
*
: d1
= +
>A097F),:L,:+d,"7F1(
d1 & d1 &( ) ( , , )( ) ( , , )
+ + − + + + =
'
< <' E<G < <N < E<G <
⇔
d 1 1 & d & 1
( , , ) ( , , )
+ − + − + − +
' '
' < <' E<G < <' E<G
z
&
( , , )
+ =
< <N < E<G <
⇔ 1 & &
d 1 d & 1
( , , ) ( , , )
( , , )
− + − + + =
+ − =
' '
< <' E<G < <N < E<G <
' < <' E<G <
 ;, F1 9>F " #$ % 
1
+ =
' '
, "7 F1(  97 F) ,: L
' '
' '
< <' E<G < <N < E<G <
' < <' E<G <
( , , ) ( , , )
( , , )
− + − + + =
+ − =
+ =
1 & &
d 1 d & 1
1
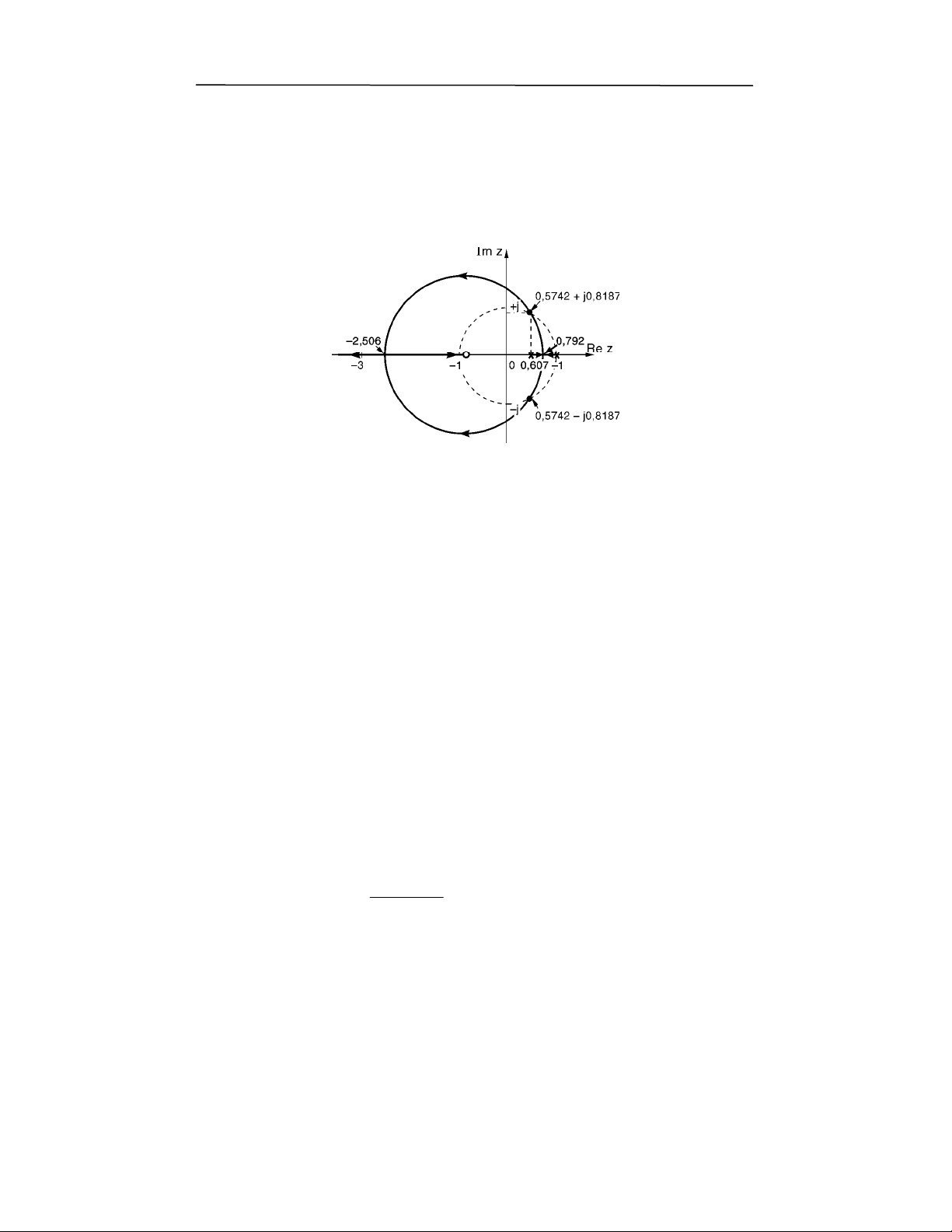
4!+3'3'
'N2
 8  97 F) ,:L , :+ d, " 7F1( R0 ;) 0 "& ! /A
:
=
d ,7F)7)>F
&
=
<
:
= −
d ,7F)7)>F
&
=
<G
: d
, ,
= ±
< 2G3' < NNG
d ,7F)7)>F
&
,
=
' NN
 *
' N
,
=

&
4)$
-6 &  N 
(0  , & Q ( "5 "7F1 ( " 9 7  ) ($8   
,0 ; ):FA : 1( RY )! 0 , ,:0 ) ( ( 6 $" +*k
Z  ,?
( )
:
d 6$ "0 @$A) 99 R; "0& 5 )7F1( "&
,L!
( )
-
Z, ? )  !
( )
? -
($ 89 7F ) ,:L , :1) ,  ($8 
:FA:1(d,7A"06$*:
( )
-
 K9 ( 71( O$ *; , "5 k  R ( ( 0 ( 0, &Q ;9Q^ ) #" $) > # 
R (  >F  (71 ( /A( K9 (71( O$ *; ," 5
0 ; >F   / + , $1(d (K 9 (7 1( O$* ;, "5  / A( K9 (7 1(  Y! ) #
,:$1( 80 ;, U0
"'
:
=d +  4  . .@ (3  >9
8(3X64.480
.6&%
"0;  >F   :FA  : 1( d ( (  , 7FA ) 6 78@ $1) " & , ?
"0 >0 1, /0; /A @$A )R &$ ,7 ( "5 ) ik

?
?
N"
m a x
%
−
=
<<
gN2h
,:0)"0k
max
/A),:5 (71( "1 ($8 ]-^e
?
/A),:5 (71( "1 ($8
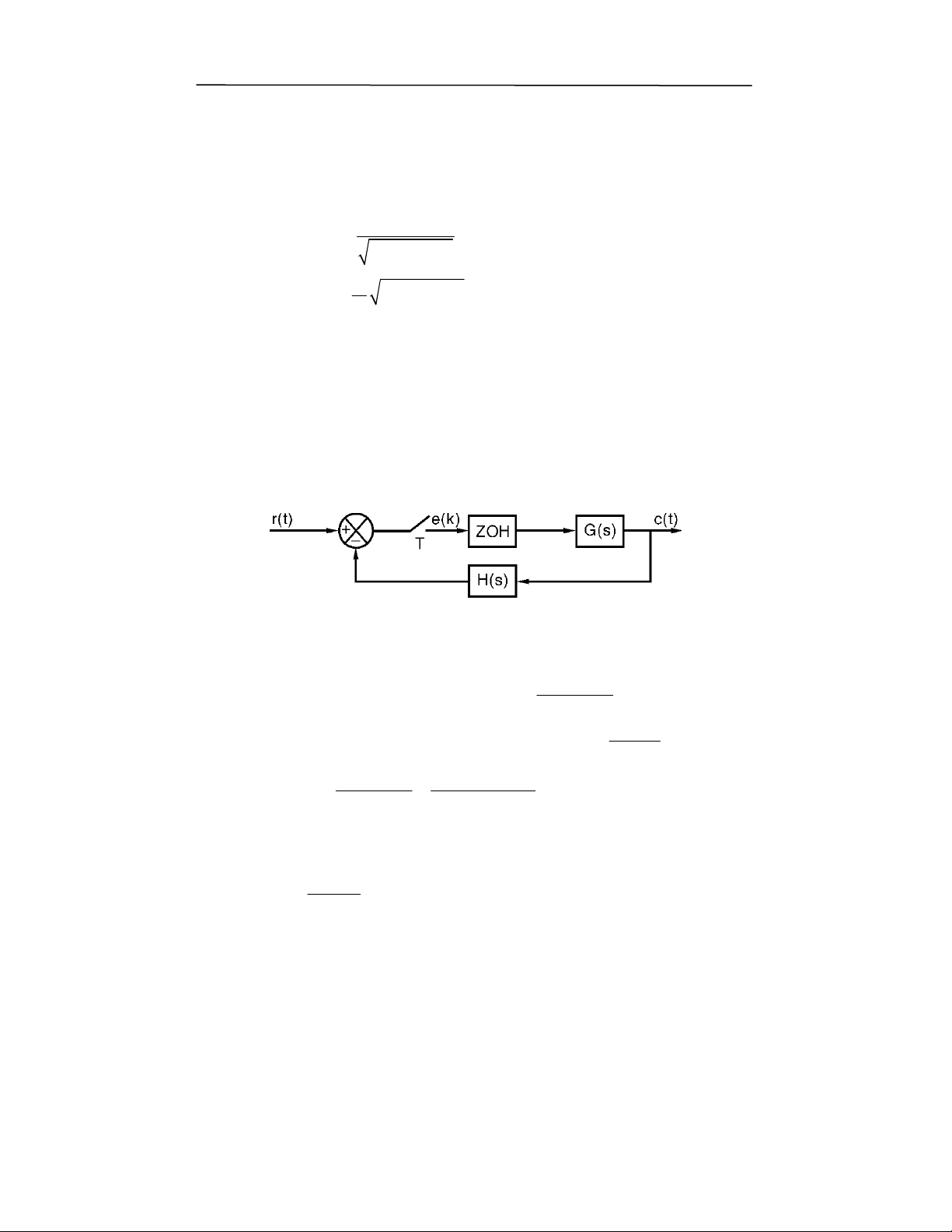
2
'NE
]-^0
(,7($P)"7F1(678@$1)%R;,(K9(71(O$*;,"5
d
: .
*
± ϕ
= ( $8    :FA  : 1( / A @71 > A0 O$  
"'
:
= "& 6$* :
)  !
'
*
d,7A"0,?"7F1(
ξ
>A
ω


.
.
ln
(ln )
−
ξ =
+ ϕ
' '
gNEh
.
"
(ln )
ω = + ϕ
' '
gNGh
H$"09@$1)(((0+),7("P,:LRA*,:0)(7F)3"&
,?N"@
?
@00
26F"I %
0"5/*),:5($0;k
? - :
- : H :
lim ( ) lim ( ) ( )
−
→∞ →
= = −
 gNNh
! 07""I %
H 6 0;Q ( / 9( $8  , 0; )" #$% & :FA : 1( ( 06F "0 # 7
,:+/Ak
? : :
a :
: H : :
P; :
( )
lim ( ) ( ) lim ( )
( )
− −
→ →
= − = − +
gNh
 ;$ ,?  $> A0 /A A ! ;( "F >5 a :
:
( )
−
=−
⇒
? :
:
P; : P; :
lim
( ) lim ( )
→→
= =
+ +
gN'<h
K,
:
& P; :
lim ( )
→
=
k<IA?C
⇒
?
&
=+
gN'h