6
N
W6561+;;;7I<;
; ,(8 ( ( %*P, $ , @ $A )"& 9 + , ?( 9 , $* ;" #$9 $1
,$ 0 ( >A 0 , ? ) +! ) K, ($8 9 ,$* ; >A R ( ($8 F8
,:1) , 6$* Q, :0) (7F) A*d ($) , 6P Q, (( %*P
,$ , ( 0 $O$ 8 > A,0 +) @$ 1) d! 01( (7 )@$1 ),71 (,;
($ 8( $ ) 7F ) A*6 P @ j :( ( % ; ,/$ > A( ( 7F )@ j
( 01 97F )9 9 , ?( F 19 ( 0 > ( 9 + ,?( >A , ; ,%; ( (
R A ,0 ($ 1, & "0; >F 9 ,$* ;
( 9 + ,?( ( ( 9 , $* ; ) - >F 671 , 0# , 1 >A 8
7F8)($8($,:L)F1d,71%?(!#!>A(7)d,7A,:jd8*
(0 ) 7F 8) >A , 10 A 9 $1 F 7P d9 8Q( " 5"9 7 )" 0;
>F (( A! "#$ > A0 "K( , :7 ) 0 % f (? (0 > ( 9+
,?( 9 ,$ *; /A % 0+ )( 0% *P ,$ , : +) A0 9 @$1 ) ,0& )
O$,(0,;,(8((RA,0
,0 ;) ) #9 ,$* ;d 6 R , 60 > F 9 , $* ; % 0+ )O$
/Fd(099678@$1)97F)99Q;9Q^,$*;,?A!!0+,8
) #"$ )(0 , & 9@$1 )(0 ( ( 9 , $* ; R ( R ;,%*A A0>A
,7 FA )@$A )" &9 , @ 0"0 ) ,: 0 ) ( ) 8O$ *; ,6P
"F )8 F #$ ; $) 8 " 5) 0P>A0 " 0;>F 9 ,$* ;/A
6>A(^(7,A9#,#60;(0*)iF8"#$:/A,A
9#(0($A),#60;>F)0P>A0
( 9 , $*; , 7FA ) " 7F1( Q ;9 Q^ R Y) > A > $A) ,$ *;
,? .7F) 99 ,$*; ,? ,7A) "01 (0 99 9+ "01
,$ *; ,? 0 R; , (7 9 ,$ *; A 0 "0; >F R ( R;, %*A
. 7F ) 9 9 ! K, 9 ` ) 9 /A !0 , % *P ,$ , "-( /71 ( "& 9 +
,?( " 97 )($ 8 !0 , 9,$* ;R ( ( 97 F)9 90&
"5 ( $8 4* 9$ 0>/A ( (% *P, $ ,! 1 !P " &Q ( "5 6 710 &
"5 F8 ,:1 ) , Q ( / 9 ($8 9 ,$*; @ 71 ,: + ,0& ) O$ ,
0 (( % ! f )/7F1 ) . 7F) 9 9 .0 90> : ;,7P$ $
( 0 > ( Q( " 5 6 71 0 & " 5 9 ,$* ; R ;, R ; , 0 , FA
) +$ ( $ & "7 FA) , :0A ,0& ) O$ , 0 (0 ,& 9 @$ 1) ( 0
9 ,$*; R; ,+ ,0 ,FA ) !A 9# ,$*; ,? %0+)
;,,;,980&"5F8>0A)F8
R ( : ;, ( 0 ( 0 > A 9 , $*; ? ,% Q78 /* R Y) (( %
! 9 + , ?( ( $) ; " # A ** +$ ( #$ @$ A) ( ( 9 7F) 9 9
60;678@$1)!*,?"&)8O$*;,$*+d/FA)8(^(0)
45
,: 5" 0; >F RA ,0 ($ 1, & "7 F1( " #( 9 0(0 , & !F 8: 0 )% ;,
O$8>A(0"7F1((()8($)"&@$A)(0((RA,0%(
.7F)99!0+908),7FA)@$A)"&%&!,:/#($0;671
0& "5 ( $8 " #$% & 9 ,$ *; . 7F ) 9 9 A* 6 P )$ 9
% -(9$ 1( #$*;$ ,0 ;7k % 0+ )" &*( ? Q (,? $ /7 1(
($ 8 ) 8 , ; , @0 ( ( %0 % f , :0) O$ ,:L 9 + ,? ( >L
97(,19
9,;
-.#/#0 !
s , 9 ,$ *; R ( g p ' h " 7F1( !0+ ,8 F8 @1 )
9 7F ),: L > 9+ R ( ; ,>F ( ( R ;, :1 ) , Q
dQ
'
k
?
? ` ? ?
?
? ` ? ?
( , )
( , )
= =
= =
'
'
' ' '
gh
0 K( "7F 1(! 0+ ,8 @7F @ 1) !0 ,9 7F ),: L
? ` ? ?
? ` ? ?
( , )
( , )
=
' ' '
'
g'h
F (( " #$ % R " #$
? ?
( ) & ( )
'
< <
+,;.
'<
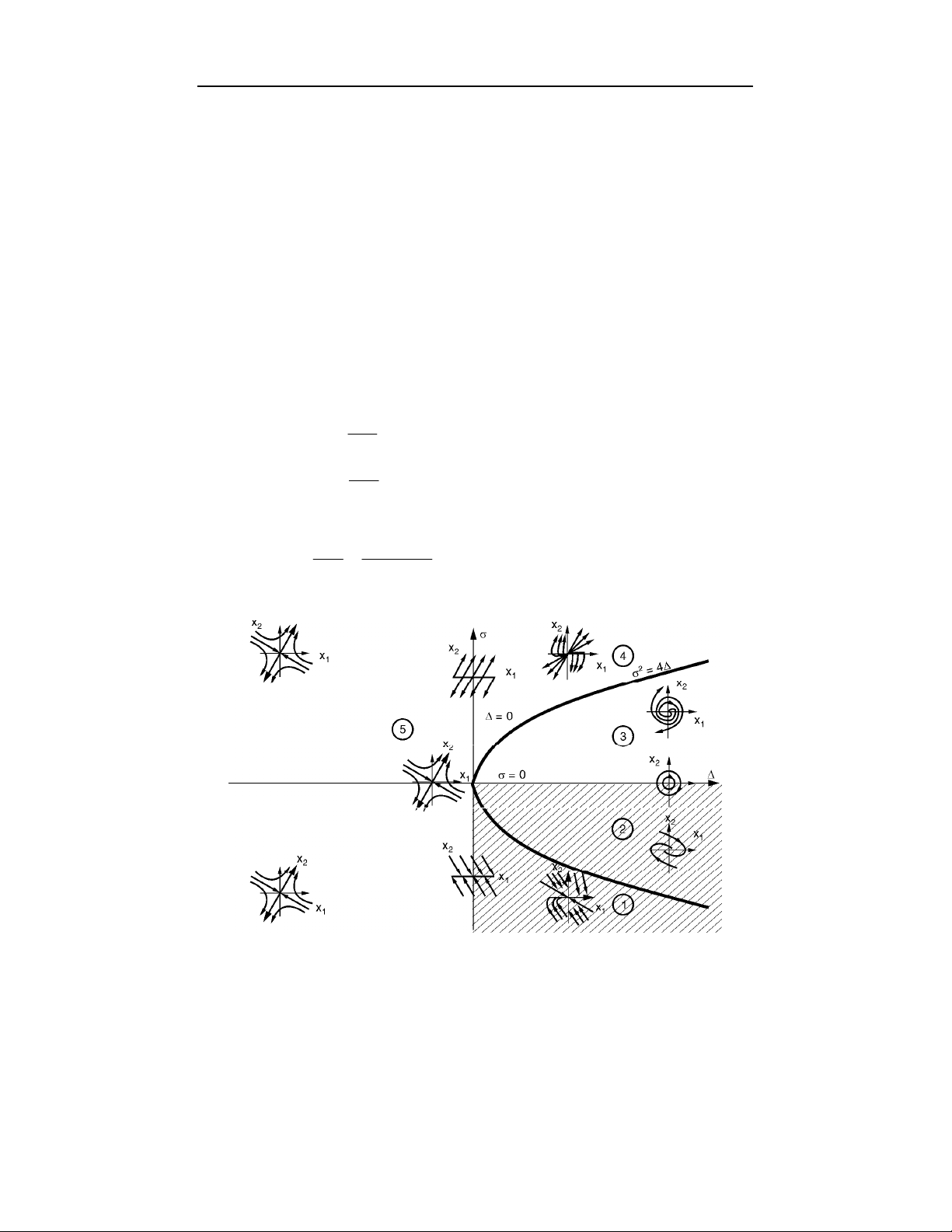
%W65
%&'(
)*+ ,-&( .!/0102-2 !2
U'
3
1
σ
∆ <
3
σ < − ∆
0
ξ >
0 3
* *
3< 3 0< 3< 3 0<
0
0 3 0 3
- * - - * -
-
* * * *
τ τ
− −
= −
− −
( ) ( )
0 3
* *
0 3< 3 0< 3 3< 3 0<
3
0 3 0 3
* - * - * - * -
-
* * * *
τ τ
− −
= −
− −
3
03
3
* 0
σ
ξ = − ∆
= −ξ ± ξ −
V'('&N
3'
0
ξ =
( )
( )
[ ]
[ ]
*
0 0< 3<
*
0 3< 3<
0 3
- - 0 * -
- - 0 - *
* * * 0
τ
τ
= − τ +
= + τ − τ
= = −
*3
σ
= −ξ =
∆
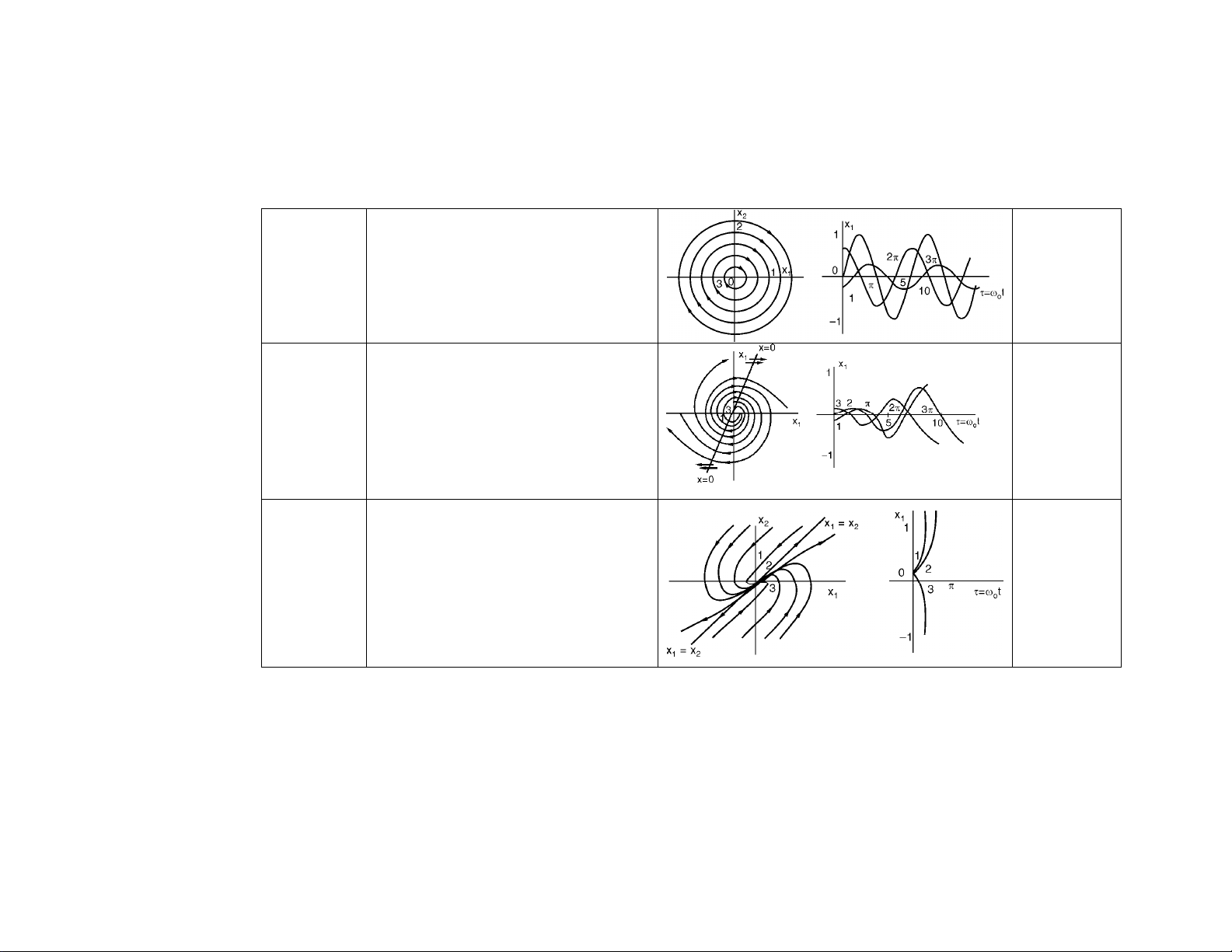
U'
< 0
< ξ <
[ cos sin ]
[ cos sin ]
3< 0<
0 0<
3< 0<
3 3<
- -
- -
- -
- -
−ξ
−ξ
+ ξ
= Ω + Ω
Ω
ξ +
= Ω − Ω
Ω
03
3
* W
0
= −ξ ± Ω
Ω = − ξ
'
V'('&N
3'
<
<
σ =
ξ =
cos sin
cos sin
0 0< 3<
0 3< 0<
3 3 3 3
0 3 0< 3<
- - -
- - -
- - - -
= τ + τ
= τ − τ
+ = +
0
Ω =
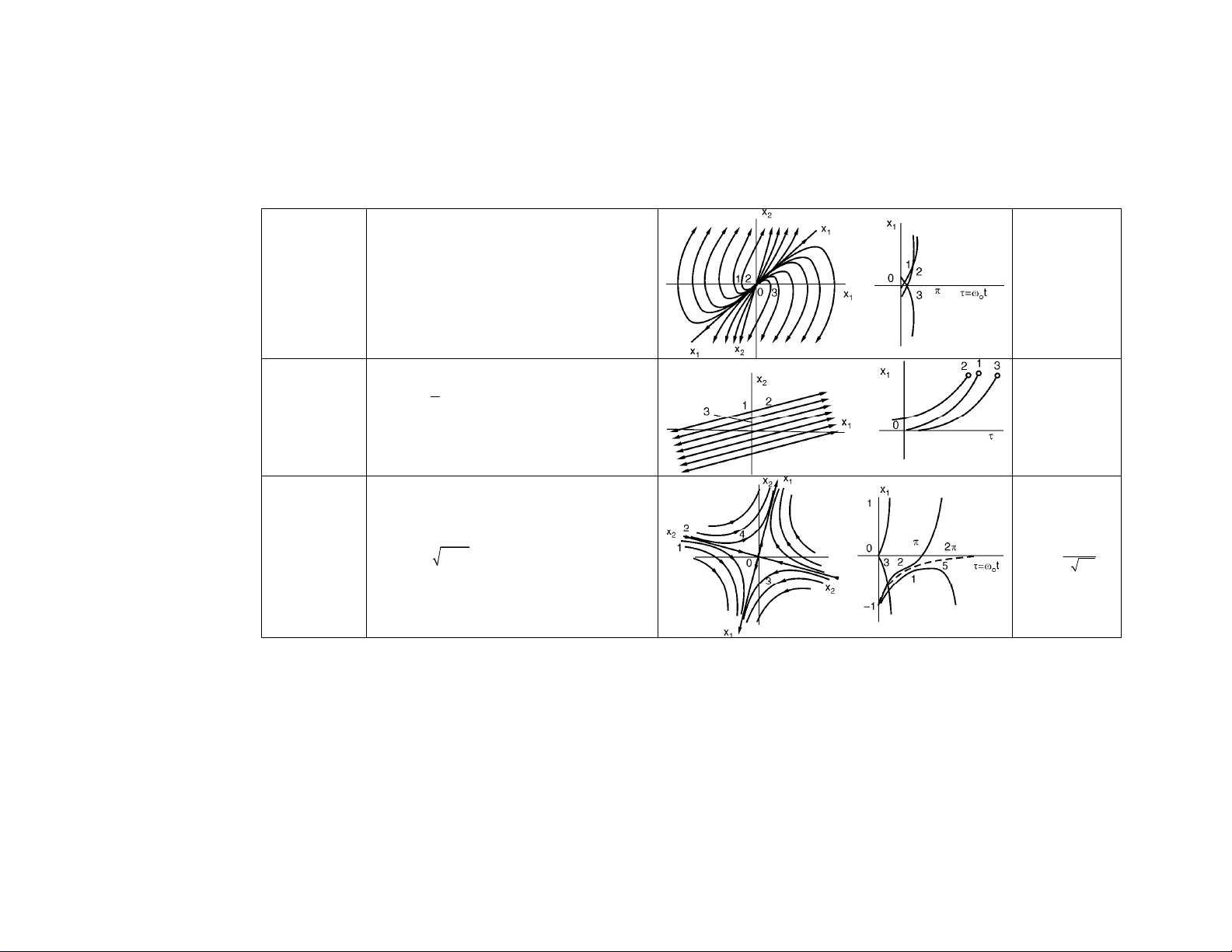
U'
0 <
− < ξ <
V'('&N
3'
0
ξ =
''
U'
0
ξ < −
V'('&N
3'
[ ]
( )
0 0< 3<
3 3<
3 3< 0 0<
0
- - - 0
- -
- - - -
τ
τ
= − −
σ
=
− = σ −
( )
<
τ = σ −
U'
<
<
∆ <
σ >
3
03
* 0
= −ξ ± ξ +
3
σ
ξ = −
−∆
![Đề cương chi tiết học phần Lý thuyết điều khiển tự động [chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2021/20210417/lovebychance01/135x160/5501618651902.jpg)
![Trắc nghiệm Điều khiển tự động [mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250924/kimphuong1001/135x160/96131758686268.jpg)
