11
CHÖÔNG II: DAÂY QUAÁN PHAÀN ÖÙNG MAÙY ÑIEÄN
XOAY CHIEÀU
§ 2.1 ÑAÏI CÖÔNG
Daây quaán maùy ñieän xoay chieàu coù nhieäm vuï caûm öùng ñöôïc söùc ñieän ñoäng
(s.ñ.ñ) nhaát ñònh ñoàng thôøi cuõng tham gia vaøo vieäc taïo neân töø tröôøng caàn thieát
cho söï bieán ñoåi naêng löôïng ñieän töø trong maùy.
Keát caáu cuûa daây quaán phaûi ñaûm baûo caùc yeâu caàu kyõ thuaät sau:
+ Tieát kieäm daây quaán (phaàn ñaàu noái).
+ Beàn veà cô, nhieät, ñieän.
+ Cheá taïo ñôn giaûn, laép raùp, söûa chöõa deã daøng.
Phaân loaïi daây quaán:
+ Theo soá pha: m = 1, 2, 3.
+ Theo soá raõnh cuûa moät pha döôùi moãi böôùc cöïc q.
+ Theo lôùp: 1 lôùp, 2 lôùp.
+ Theo hình daïng phaàn ñaàu noái: daây quaán ñoàng khuoân, ñoàng taâm, xeáp, soùng
.v.v.v...
Thöôøng thì soá raõnh cuûa 1 pha döôùi moät cöïc q laø soá nguyeân nhöng trong moät
soá tröôøng hôïp caàn thieát q coù theå laø phaân soá. Daây quaán maùy ñieän xoay chieàu coù
theå ñaët trong raõnh thaønh 1 lôùp hoaëc 2 lôùp vaø töông öùng laø daây quaán 1 lôùp vaø 2
lôùp. Trong thöïc teá raát nhieàu loaïi daây quaán, trong phaàn naøy ta ñeà caäp ñeán 1, 2 loaïi
phoå bieán thöôøng gaëp vaø moãi loaïi chæ neâu phöông phaùp phaân tích vaø sô ñoà noái
daây.
§ 2.2. DAÂY QUAÁN 3 PHA COÙ Q LAØ SOÁ NGUYEÂN
1. Daây quaán 1 lôùp:
Thöôøng ñöôïc duøng cho caùc ñoäng cô ñieän coù coâng suaát < 7kW. Trong moãi
raõnh chæ ñaët 1 caïnh taùc duïng neân soá boái daây S = Z/2.
Thí duï: Veõ sô ñoà khai trieån daây quaán kieåu ñoàng khuoân taäp trung 1 lôùp,
Z = 24, 2p = 4.
• Trình töï xaây döïng sô ñoà daây quaán 1 lôùp vôùi q laø soá nguyeân:
- Xaùc ñònh goùc ñoä ñieän giöõa 2 raõnh lieân tieáp:
0
00
30
24
3602
Z
360p ===α ..
ñ
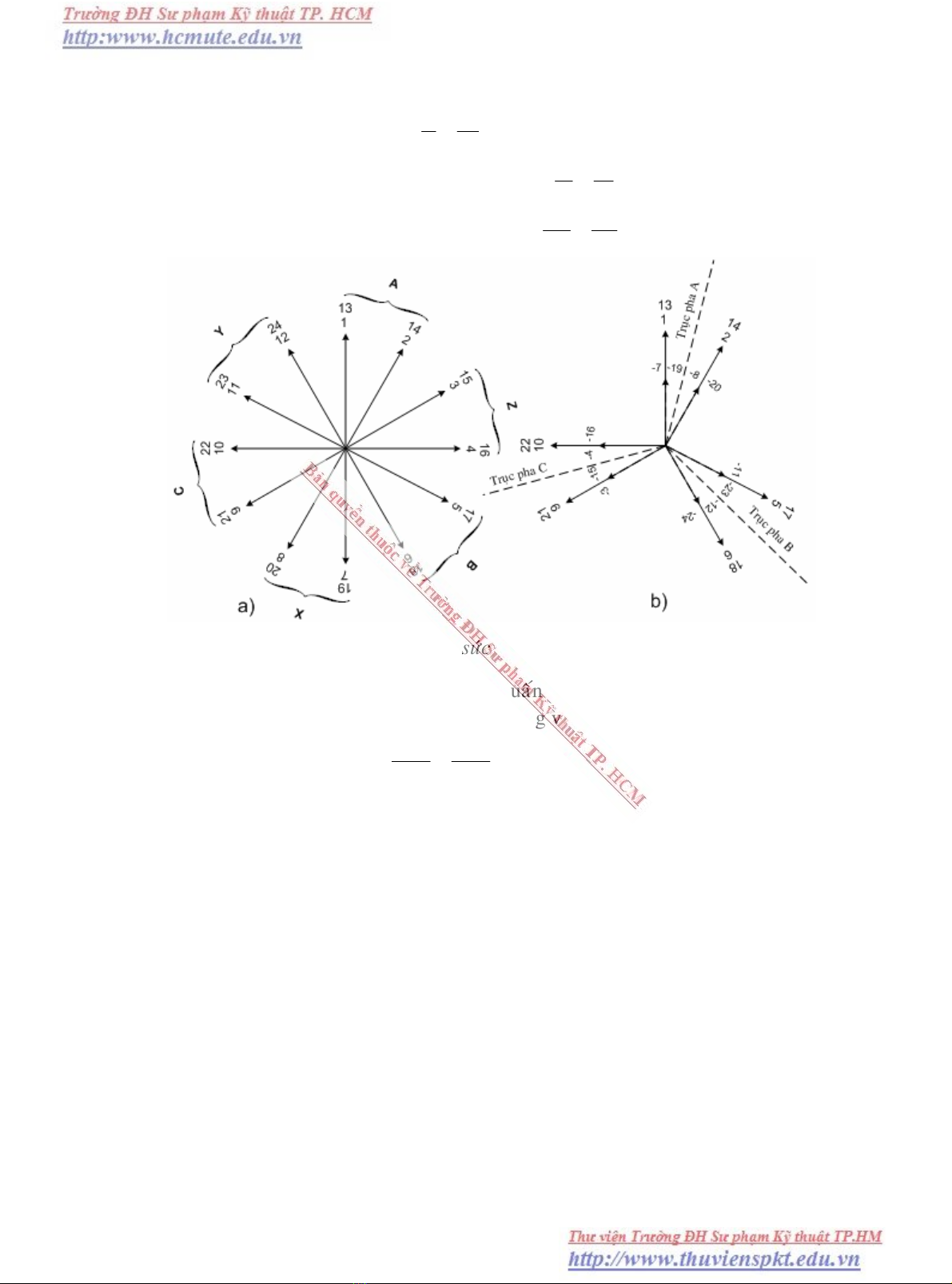
Neân caïnh taùc duïng töø 1 ñeán 12 döôùi ñoâi cöïc thöù nhaát laøm thaønh hình sao
s.ñ.ñ coù 12 tia nhö hình 2 -1a. Do vò trí caùc caïnh 13 ñeán 24 döôùi ñoâi cöïc thöù 2
hoaøn toaøn gioáng vò trí cuûa caùc caïnh 1 ñeán 12 döôùi ñoâi cöïc thöù nhaát neân s.ñ.ñ cuûa
chuùng ñöôïc bieåu thò baèng hình sao s.ñ.ñ truøng vôùi hình sao s.ñ.ñ thöù nhaát.
- Soá raõnh cuûa 1 pha döôùi 1 cöïc:
2
232
24
mp2
Z
q=== ..
12
- Soá phaàn töû daây quaán:
12
2
24
2
Z
S===
- Soá phaàn töû daây quaán trong moät pha: 4
3
12
m
S
Sfa ===
- Soá nhoùm boái daây trong moät pha: 2
23
12
mq
S
n=== .
So saùnh vôùi soá ñoâi cöïc 2p ta suy ra daây quaán ñaáu cöïc giaû.
- Pha A caùch pha B laø 1200 ñieän töông ñöông vôùi:
4
30
120120
0
00
==
αñ
raõnh.
- Böôùc daây quaán .6y =τ=
- Giaûn ñoà khai trieån daây quaán:
H
ình 2.1 Hình sao söùc ñieän ñoäng 12 tia
13
2. Daây quaán 2 lôùp:
Laø loaïi daây quaán maø trong moãi
raõnh ñaët 2 caïnh taùc duïng, neân soá phaàn
töû baèng soá raõnh cuûa loõi theùp ⇒S = Z.
so vôùi daây quaán 1 lôùp daây quaán 2 lôùp
coù nhöõng öu ñieåm sau:
- Loaïi naøy coù theå thöïc hieän ñöôïc
böôùc ngaén laøm giaûm söùc ñieän ñoäng
baäc cao, caûi thieän ñöôïc daïng soùng söùc
ñieän ñoäng, ñaëc tính laøm vieäc cuûa maùy
toát hôn.
- Ñaàu noái cuûa caùc boái daây chaéc
chaén, goïn, ít choaùn choã, traùnh ñöôïc
phaàn ñaàu noái chaïm vaøo naép maùy.
Tuy nhieân vieäc loàng daây cuõng nhö söûa chöõa gaëp nhieàu khoù khaên hôn trong daây
quaán 1 lôùp.
Coù 2 kieåu daây quaán: Quaán xeáp vaø quaán soùng, ña soá duøng daây quaán xeáp.
Daây quaán soùng chæ duøng vôùi rotor daây quaán cuûa ñoäng cô ñieän khoâng ñoàng boä.
a) Daây quaán xeáp:
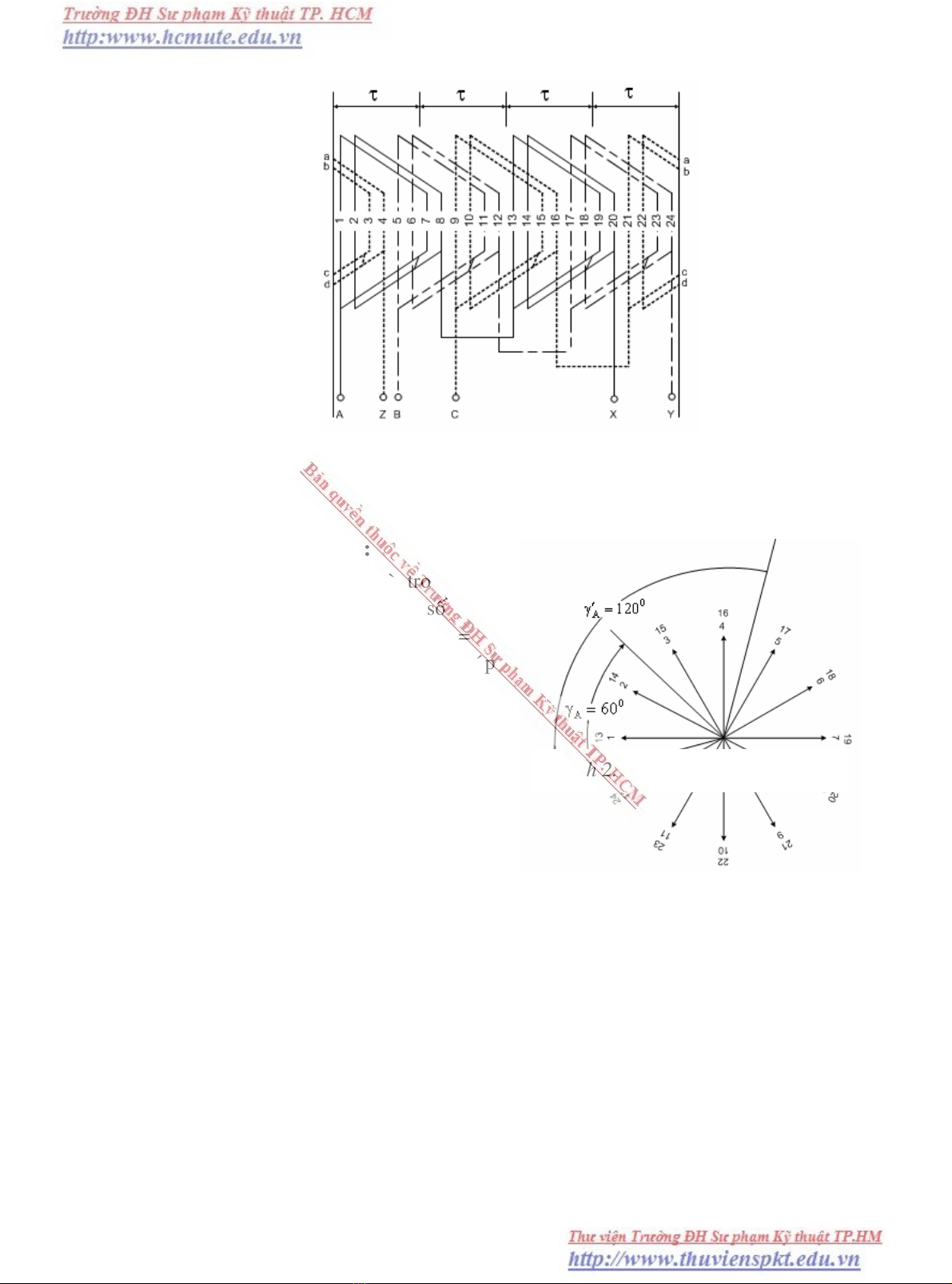
Thí duï: Veõ sô ñoà khai trieån daây quaán xeáp 3 pha, 2 lôùp vôùi Z = 24, 2p = 4.
• Trình töï xaây döïng sô ñoà daây quaán xeáp 3 pha 2 lôùp vôùi q laø soá nguyeân:
1. Veõ hình tia söùc ñieän ñoäng.
H
ình 2.2 Sô ñoà khai
t
rieån daây quaán 3 pha 1 lôùp ñoàng
khuoân taäp trung vôùi Z = 24; 2p = 4; q = 2.
H
ình 2.3 Hình tia söùc ñieän ñoäng
14
0
00
30
24
3602
Z
360p ===α ..
ñ
p2
Z
=τ : böôùc cöïc
τ
=β y: heä soá ruùt ngaén böôùc daây
y: böôùc daây
- Soá raõnh cuûa 1 pha döôùi 1 böôùc cöïc:
2
232
24
mp2
Z
q=== ..
- Soá phaàn töû daây quaán: S = Z = 24
- Soá phaàn töû trong 1 pha: 8
3
24
m
S
Spha ===
- Soá nhoùm boái daây trong 1 pha:
n = 2p ⇒ ñaáu cöïc thaät (c – c, ñ - ñ)
2. Böôùc daây quaán: Quaán böôùc ngaén 6
5
65y
5y ==
β
=τ⇒=τβ= .
.
AA ZZ BB XX CC yy AA ZZ BB XX CC yy
A ZZ BB XX CC yy AA ZZ BB XX CC yy A
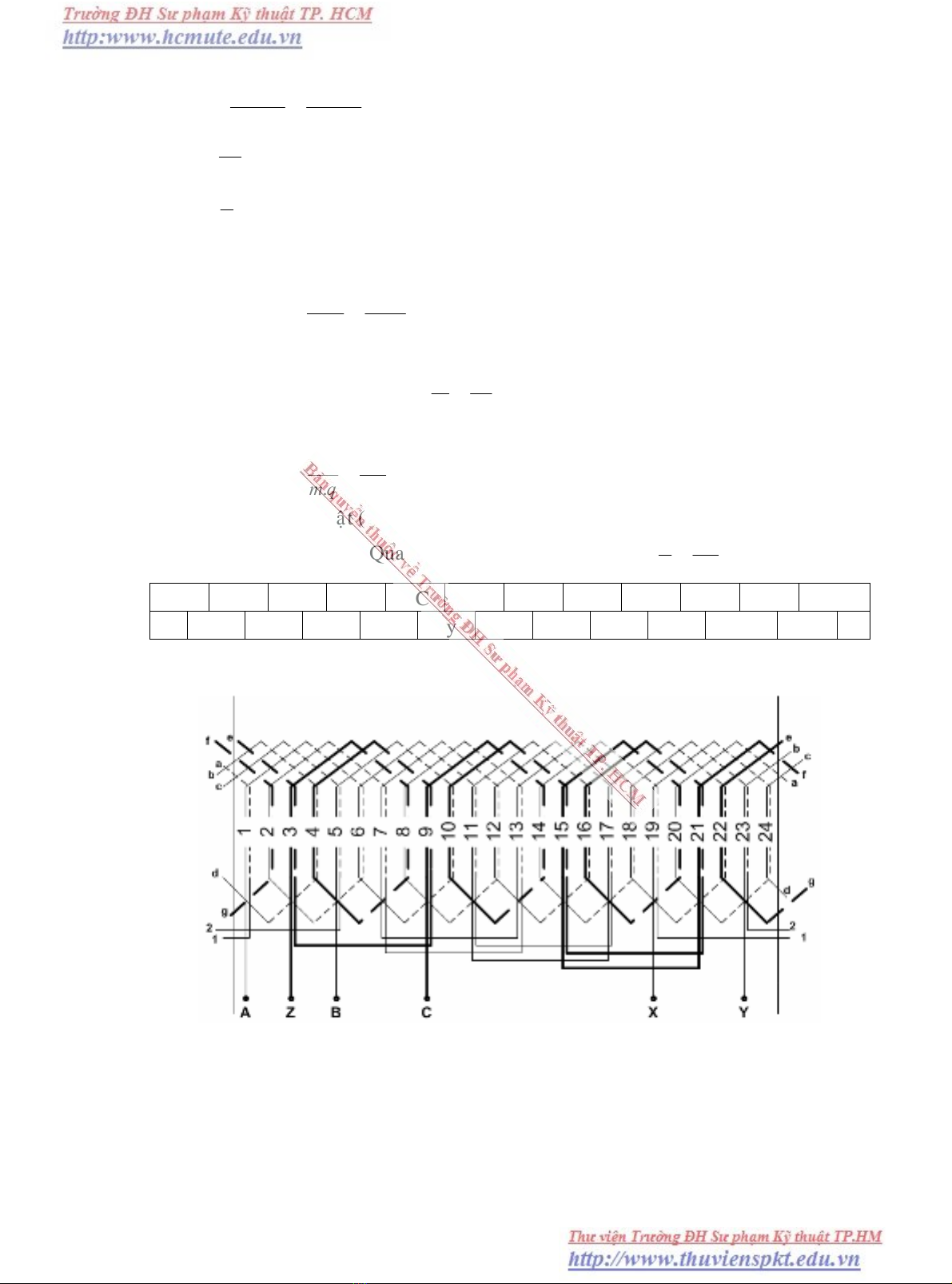
Caùch veõ: Ñaàu tieân ta phaân boá cuoän daây theo vuøng pha vôùi q = 2 cho moãi
vuøng. Neáu raõnh 1 vaø 2 thuoäc vuøng pha A thì vuøng pha B phaûi ñaët ôû raõnh 5, 6 vì
pha B caàn phaûi dòch chuyeån so vôùi pha A laø 1200 töùc 4 raõnh (1 + 4 = 5, 2 + 4 = 6).
4
2.3
24
.=== qm
S
n
H
ình 2.4 Daây quaán xeáp 2 lôùp vôùi Z = 24, 2p = 2, q = 5, β =5/6.
15
Pha C cuõng dòch chuyeån töông ñoái vôùi pha B vaø chieám caùc raõnh (5 + 4 = 9, 6 + 4
= 10). Coøn khoaûng raõnh töø 13…24 cuõng ñöôïc phaân boá xen keõ caùc pha A, B, C vôùi
cuøng 1 quy luaät nhö vaäy (pha A: 13, 14, pha B: 17, 18, pha C: 21, 22). Nhö vaäy
moät nöûa vuøng pha vaø lôùp treân ñaõ ñöôïc phaân boá, coøn caùc vuøng pha khaùc cuõng
ñöôïc phaân boá theo caùc pha A, B, C vaø ñöôïc kí hieäu töông öùng X, Y, Z. Luùc naøy
vuøng X thuoäc pha A dòch chuyeån so vôùi vuøng A laø t = 6 töùc laø ôû caùc raõnh (1 + 6 =
7, 2 + 6 = 8, 13 + 6 = 19, 14 + 6 = 20). Töông töï vuøng Y thuoäc pha B ôû caùc raõnh
(5 + 6 = 11, 6 + 6 = 12, 17 + 6 = 23, 18 + 6 = 24). Coøn vuøng Z thuoäc pha C ôû caùc
raõnh (9 – 6 = 3, 10 – 6 = 4, 21 – 6 = 15, 22 – 6 = 16). Söï khaùc nhau ôû caùc vuøng
pha A, B, C vaø X, Y, Z laø söùc ñieän ñoäng ôû caùc caïnh töông öùng cuûa noù.
b) Daây quaán soùng:
Trình töï xaây döïng sô ñoà daây quaán soùng hai lôùp:
Böôùc 1: Laáy soá lieäu Z, 2p. Suy ra
vaø kieåm tra laïi caùc ñieàu kieän Z vaø τ.
Böôùc 2: Choïn böôùc quaán daây toång hôïp y
p
bZ
y)( ±
=
Khi Z = np (n laø soá nguyeân) choïn b = 0. Tröôøng hôïp naøy töông öùng vôùi Z
laø boäi soá cuûa p.
Khi soá caïnh taùc duïng trong raõnh laø 2 hay laø boäi soá cuûa 2 (4, 6, 8,…) ta
thöôøng choïn b = 1.
Khi trong moät raõnh chæ coù moät caïnh taùc duïng, ta choïn b = 2.
Böôùc 3: Goïi N laø toång soá caïnh taùc duïng cuûa boä daây quaán.
¾ Neáu (N/6) laø soá chaün thì moät nhaùnh trong moät pha coù (N/6) caïnh taùc duïng.
¾ Neáu (N/6) laø soá leû thì moät nhaùnh trong moät pha coù ( 1
6−
N) caïnh taùc duïng,
nhaùnh coøn laïi coù ( 1
6+
N) caïnh taùc duïng.
Böôùc 4: Laäp baûng soá xaùc ñònh caùch quaán daây, baûng soá thieát laäp nhö sau:
• Chia baûng daây quaán thaønh 2p coät.
• Laàn löôït ghi lôùp treân, lôùp döôùi, lôùp treân, lôùp döôùi, … vaøo ñaàu moãi coät bieåu
thò cho caïnh taùc duïng treân vaø döôùi cuûa moãi boái daây. Sau ñoù, ghi soá thöù töï
raõnh vaøo moãi oâ. Goïi y1 laø böôùc boái daây vaø böôùc y2 tính nhö sau:
y
2 = y – y1.
Ta ghi soá sau caùch soá tröôùc moät böôùc y1, roài y2.
• Moãi khi ghi heát moät doøng, tröôùc khi vieát oâ ñaàu cuûa doøng tieáp theo, ta xem
maïch coù bò kheùp kín sôùm hay khoâng. Neáu coù söï kheùp kín maïch sôùm thì
phaûi taêng hay giaûm böôùc y2 moät ñôn vò.
• Neáu sô ñoà quaán duøng cho stator thì phaûi tieán haønh bieän phaùp vöøa neâu bình
thöôøng ôû treân, ngöôïc laïi neáu daây quaán duøng cho rotor ta phaûi chuù yù caùch
ñaët ñaàu daây vaøo moãi pha ôû caùc soá raõnh 1; ⎟
⎠
⎞
⎜
⎝
⎛+3
Z
1; vaø ⎟
⎠
⎞
⎜
⎝
⎛+3
Z2
1 vaøo vò trí oâ
thích hôïp ñöùng ñaàu moãi nhaùnh (tröø tröôøng hôïp 2p laø boäi soá cuûa 3).