56
ø
Chöông 6 : ÑOÅI CHIEÀU
§ 6.1. Ñaïi Cöông
Khi maùy ñieän moät chieàu laøm vieäc phaàn öùng quay troøn, caùc phaàn töû daây quaán
seõ laàn löôït ñi vaøo vuøng trung tính ôû döôùi choåi than, doøng ñieän trong caùc phaàn töû seõ
laàn löôït thay nhau ñoåi chieàu khi chuyeån töø maïch nhaùnh naøy sang maïch nhaùnh kia.
Quaù trình ñoåi chieàu cuûa doøng ñieän khi phaàn töû di chuyeån trong vuøng trung
tính vaø bò choåi than noái ngaén maïch ñöôïc goïi laø söï ñoåi chieàu.
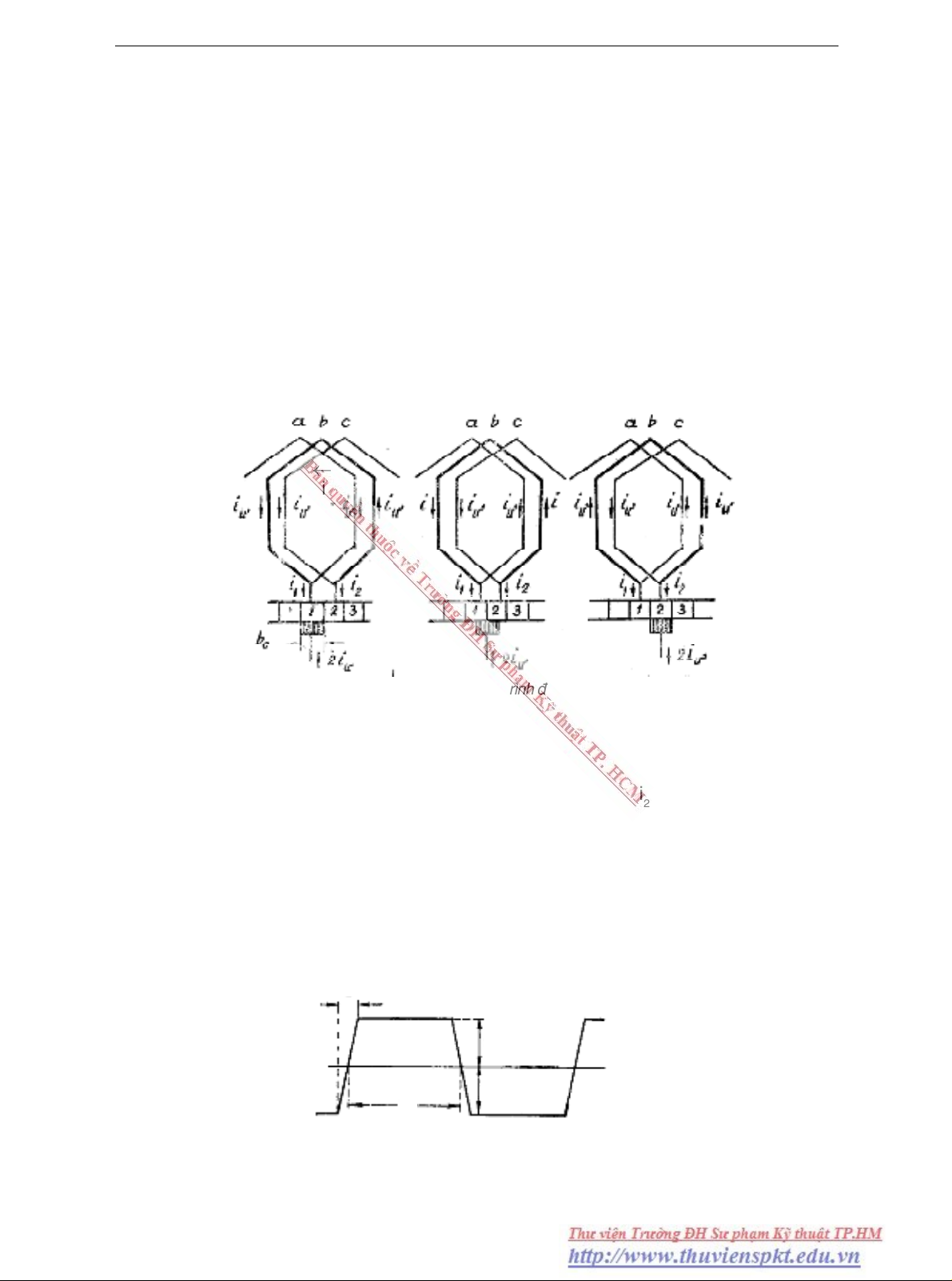
Ñeå coù khaùi nieäm cuï theå hình 6-1 trình baøy quaù trình ñoåi chieàu doøng ñieän
trong phaàn töû b cuûa daây quaán xeáp ñôn.
t = 0
i
1
= 2i
ö
i
2
= 0
i = + i
ö
0 < t <T
ñc
i
1
≠ 0
i
2
≠ 0
t = T
ñc
i
1
= 0
i
2
= 2i
ö
i = - i
ö
Hình 6.1 Quaù trình ñoåi chieàu
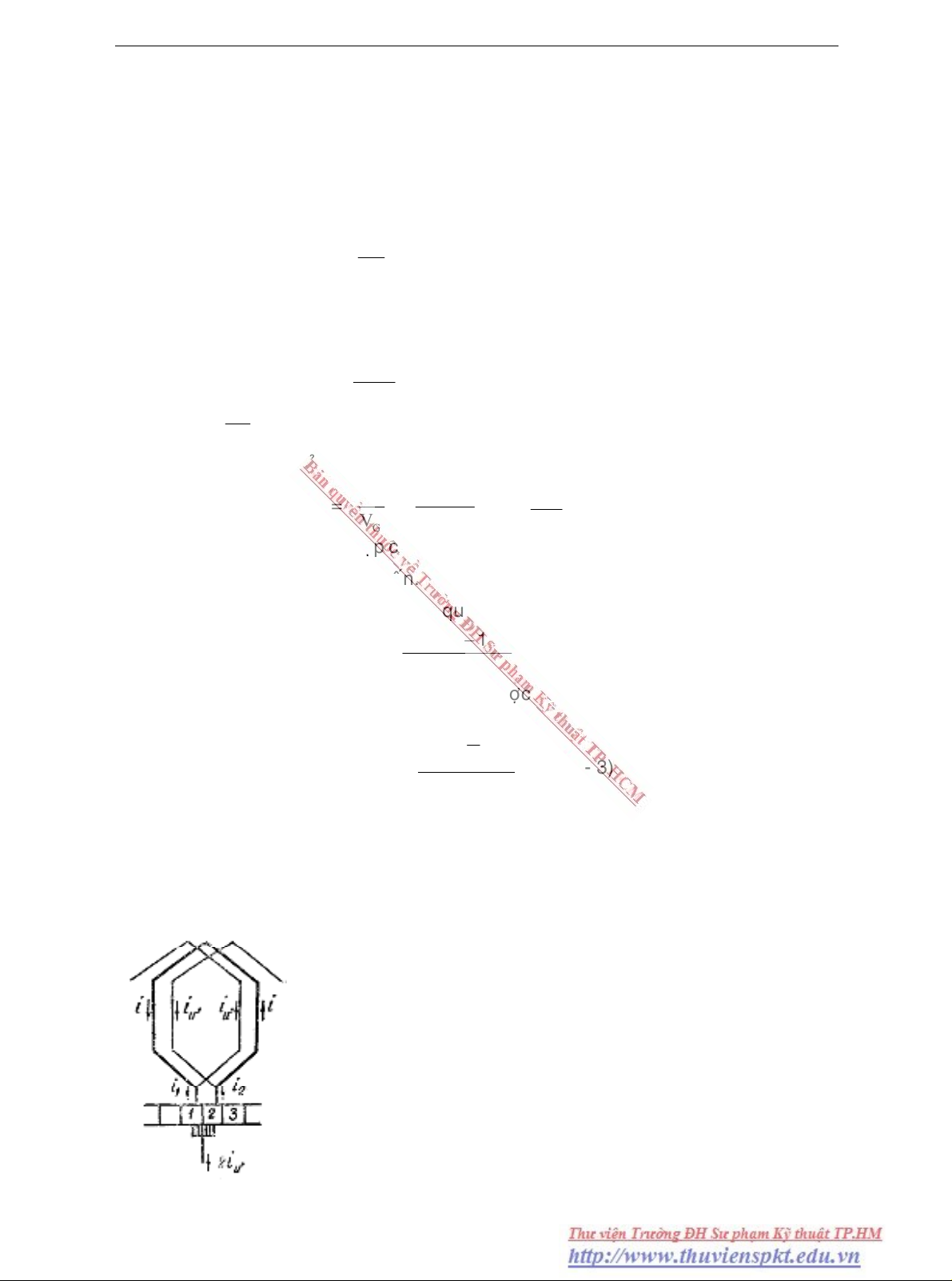
Hình 6. 2 Ñöôøng bieåu dieãn
doøng ñieän cuûa phaàn töû
Sau 1 thôøi gian T
ñc
goïi laø chu kyø ñoåi chieàu cuûa phaàn töû, doøng ñieän trong phaàn töû b
thay ñoåi töø + i
ö
cho ñeán – i
ö
nghóa laø thay ñoåi 2i
ö
. Quaù trình ñoù goïi laø quaù trình ñoåi
chieàu.
Ñöôøng bieåu dieãn doøng ñieän cuûa phaàn töû
Tñc
Tn
-iö
+iö
→
→
i
i
→
57
ø
T
n
: laø thôøi gian maø sau khi keát thuùc ñoåi chieàu phaàn töû chuyeån töø choåi than ñaõ bieát
ñeán choåi than khaùc daáu beân caïnh (thöôøng T
ñc
0,001s , T
n
0,02s) cho neân ñöôøng
bieåu dieãn doøng ñieän trong phaàn töû khi phaàn öùng quay coù daïng nhö hình 6-2.
Chu kyø ñoåi chieàu T
ñc
: laø khoaûng thôøi gian caàn thieát ñeå vaønh goùp quay ñi 1 goùc öùng
vôùi beà roäng choåi than nghóa laø :
T
ñc
=
G
c
V
b
b
c
: beà roäng choåi than; V
G
: toác ñoä daøi cuûa vaønh goùp
Goïi D
G
laø ñöôøng kính cuûa vaønh goùp
b
G
= G
D
G
πböôùc goùp (beà roäng cuûa phieán goùp)
Ñaët
G
c
Gb
b
=β
,V
G
= πD
G
.n = b
G
.G.n; n: Toác ñoä quay cuûa phaàn öùng.
Thì chu kì ñoåi chieàu cuûa daây quaán xeáp ñôn coù daïng :
T
ñc
=
G
c
V
b = .G.nb
b
G
c
=
G
βG.n
1
Ñoái vôùi daây quaán xeáp phöùc taïp coù böôùc vaønh goùp y
G
= m (m khaùc 1) thì giöõa ñaàu vaø
cuoái moãi phaàn töû coù (m-1) phieán. Vì theá phaàn töû seõ bò choåi han noái ngaén maïch
trong khoaûng thôøi gian ñeå vaønh goùp quay ñi moät cung b
c
- (m-1)b
G
, do ñoù
Thay b
c
= β
G
b
G
, m = a/p vaø v
G
= b
G
.G.n ta ñöôïc
Quaù trình ñoåi chieàu tuy xaûy ra raát ngaén (T
ñc
0,001s) nhöng neáu ñoåi chieàu khoâng
toát thöôøng sinh ra tia löûa lôùn döôùi choåi than hoaëc taïo thaønh voøng löûa giöõa hai choåi
than aûnh höôûng xaáu ñeán quaù trình laøm vieäc cuûa maùy.
§ 6.2. Quaù trình ñoåi chieàu
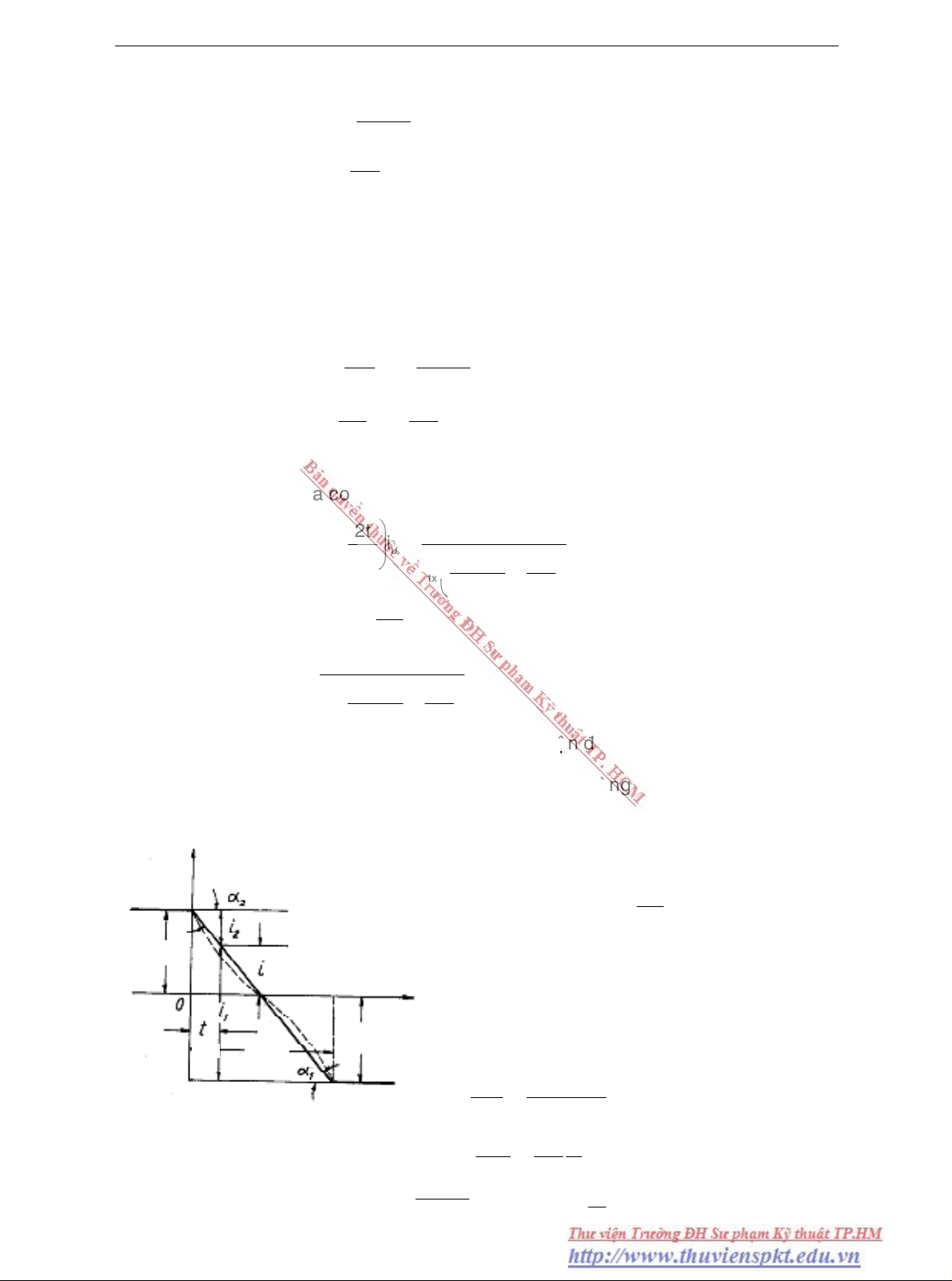
Hình 6.3
Ta haõy nghieân cöùu qui luaät ñoåi chieàu xaûy ra ôû phaàn töû cuûa
daây quaán xeáp ñôn treân hình 6-3. Theo ñònh luaät kirkhoff2
vieát cho maïch voøng cuûa phaàn töû abc ta coù :
i.r
pt
+ i
1
(r
d
+ r
tx1
) – i
2
(r
d
+ r
tx2
) = Σe
Neáu tính gaàn ñuùng ta giaû thieát r
pt
= 0, r
d
= 0 ta coù:
i
1
r
tx1
– i
2
r
tx2
= Σe (6-4)
Trong ñoù:
i : doøng ñieän ngaén maïch chaïy trong phaàn töû ñoåi chieàu.
≈ ≈
(6 - 1)
( )
G
Gc
v
b1mb
T−−
=
≈
(6 - 2)
nG
1
p
a
T
G
ñc
.
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛−−β
=(6 - 3)
c
a
b
58
ø
i
1
, i
2
: doøng ñieän chaïy qua daây noái vôùi caùc phieán goùp 1,2.
r
pt
: ñieän trôû cuûa phaàn töû. r
d
: ñieän trôû cuûa daây noái.
r
tx1
, r
tx2
: ñieän trôû tieáp xuùc cuûa choåi than vôùi phieán ñoåi chieàu1 vaø 2.
Σe : toång caùc s.ñ.ñ caûm öùng trong phaàn töû ñoåi chieàu bao goàm :
S.ñ.ñ töï caûm e
L
: phaàn töû ñoåi chieàu coù heä soá töï caûm L
c
do ñoù khi ñoåi chieàu, trong
phaàn töû seõn caûm öùng neân moät söùc ñieän ñoäng.
e
L
= – L
c
dt
di
Khi ñoåi chieàu doøng ñieän thay ñoåi töø i = + i
ö
(khi t = 0) ñeán i = – i
ö
(khi t = T
ñc
), töø
ñoù suy ra dt
di < 0 suy ra e
L
> 0. Theo ñònh luaät Lenzt e
L
coù xu höôùng laøm cho söï
ñoåi chieàu chaäm laïi.
Giaù trò trung bình cuûa s.ñ.ñ töï caûm :
e
Ltb
=
∫
−
+
−
ö
ö
i
i
c
ñc
dt
di
L
T
1 = ö
ö
i
i
ñc
c
i
T
L
−
+
−|
= L
c
ñc
ö
T
2i
S.ñ.ñ hoã caûm e
M
: Do aûnh höôûng cuûa söï ñoåi chieàu ñoàng thôøi cuûa caùc phaàn töû khaùc
naèm trong cuøng moät raõnh. Söùc ñieän ñoäng hoã caûm e
M
Suy ra giaù trò s.ñ.ñ hoã caûm trung bình trong phaàn töû ñoåi
chieàu laø:
S.ñ.ñ ñoåi chieàu e
ñc
: Sinh ra khi phaàn töû ñoåi chieàu chuyeån ñoäng trong töø tröôøng
toång hôïp taïi vuøng trung tính.
S.ñ.ñ e
L
vaø e
M
coù taùc duïng vôùi quaù trình ñoåi chieàu vaø caùch tính toaùn nhö nhau vaø
toång cuûa chuùng ñöôïc goïi laø s.ñ.ñ phaûn khaùng e
pk
= e
L
+ e
M
Ñeå quaù trình ñoåi chieàu ñöôïc tieán haønh thuaän lôïi thì e
ñc
luoân luoân phaûi ngöôïc vôùi e
pk
.
Theo ñònh luaät kirkhoff1, coù theå vieát phöông trình doøng ñieän laàn löôït taïi caùc ñieåm
nuùt a vaø c nhö sau :
Nuùt a: i
ö
+ i – i
1
= 0
Nuùt c: i
ö
– i – i
2
= 0 (6-5)
Thay caùc giaù trò cuûa i
1
, i
2
vaøo bieåu thöùc (6-1) ta coù :
i =
tx2tx1
ö
tx1tx2
tx1tx2 rr
e
i
rr
rr
+
+
+
−
∑
(6-6)
Neáu giaû thieát quaù trình ñoåi chieàu baét ñaàu töø t = 0 vaø keát thuùc khi t =T
ñc
vôùi ñieàu kieän
∑∑
−==
=
dt
di
eee
n
n
n
1n MnM
∑
=n
ñc
ö
tb
MM
T
i2
e
()
ñc
ö
nc
tb
pk
T
i2
MLe
∑
+=
59
ø
b
c
= b
G
ta coù:
S
tx1
= S
T
tT
ñc
ñc −
Trong ñoù
S
tx1
, S
tx2
: dieän tích tieáp xuùc giöõa choåi than vaø phieán goùp 1, 2.
S : laø dieän tích beà maët tieáp xuùc toaøn phaàn giöõa choåi than vaø phieán ñoåi goùp.
Vì r
tx1
, r
tx2
tæ leä nghòch vôùi S
tx1
, S
tx2
neân:
r
tx1
= tx
ñc
ñc
tx
tx1
r
tT
T
r
S
S
−
=
r
tx
: ñieän trôû tieáp xuùc toaøn phaàn öùng vôùi maët tieáp xuùc toaøn phaàn S
tx
.
Thay (6-8) vaøo (6-6) ta coù quan heä giöõa i vaø t nhö sau :
Ñaët i
c
= (1 -
ñc
T
2t ).i
ö
i
c
: goïi laø doøng ñieän ñoåi chieàu chính hay laø doøng ñieän ñoåi chieàu ñöôøng thaúng
i
f
: doøng ñieän ñoåi chieàu phuï hay doøng ñieän ñoåi chieàu ñöôøng cong.
1. Doøng ñieän ñoåi chieàu ñöôøng thaúng :
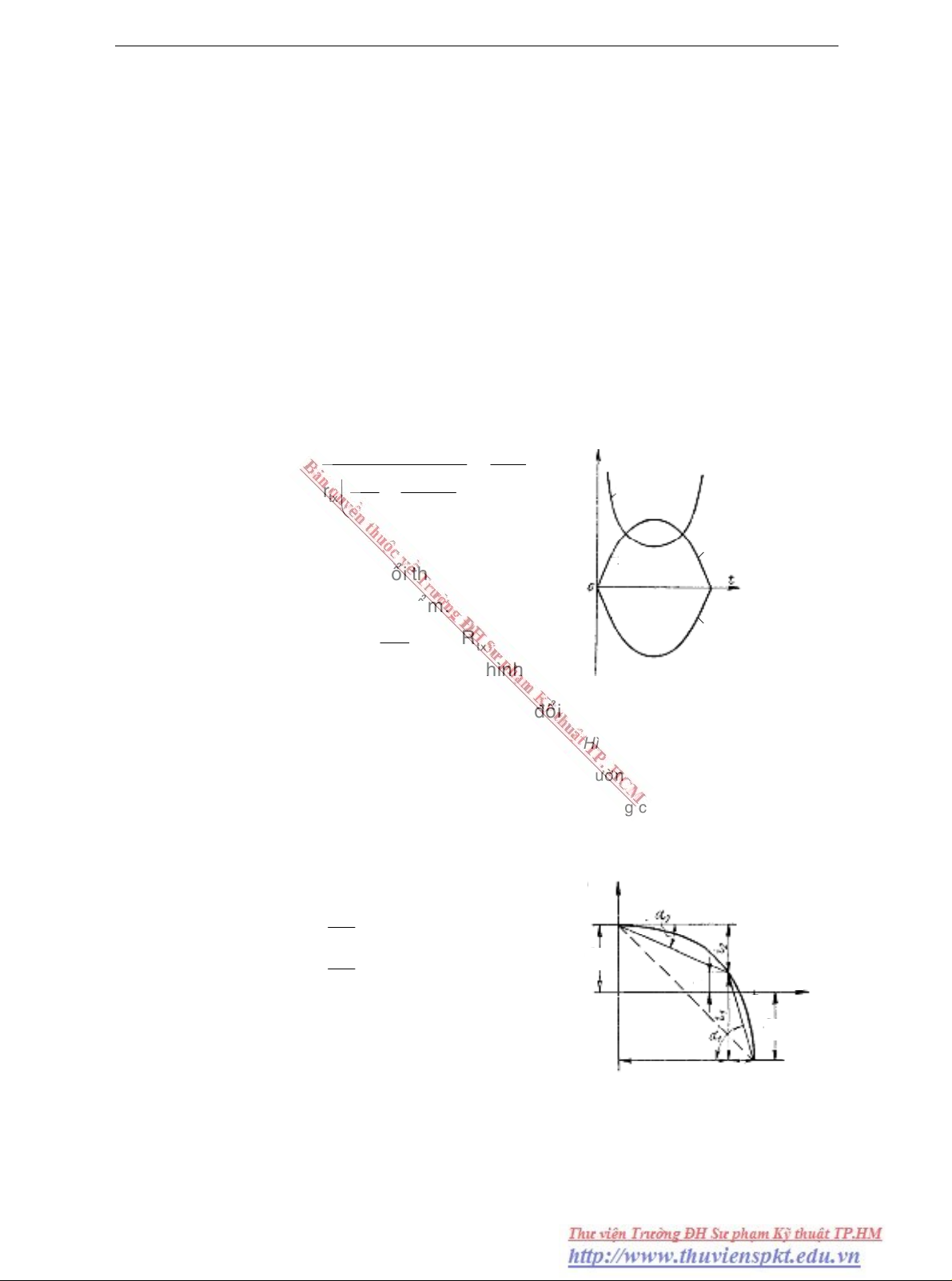
Hình 6.4 Ñoåi chieàu ñöôøng thaúng
Xaûy ra khi e
ñc
= e
pk
(toång Σe = 0)
Khi ñoù : i = (1 -
ñc
T
2t ).i
ö
= i
c
Ñöôøng bieåu dieãn doøng ñieän i = f(t) trong tröôøng
hôïp naøy laø ñöôøng thaúng nhö h6- 4.
Neáu goïi J
1
, J
2
laø maät ñoä doøng ñieän ôû beà maët
tieáp xuùc phía ñi ra vaø phía ñi vaøo choåi than thì:
Töø ñoà thò ta nhaän thaáy : 1
ñc
1tg
tT
iα=
− vaø 2
2tg
t
iα=
S
T
t
S
ñc
2tx
=
(6-7)
tx
ñc
tx
tx
2tx
r
t
T
r
S
S
r== (6-8)
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛+
−
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛−=
∑
t
T
tT
T
r
e
i
T
t2
1i
ñc
ñc
ñc
tx
ö
ñc
(6-9)
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛+
−
=
∑
t
T
tT
T
r
e
i
ñc
ñc
ñc
tx
f
Vaø
(6-10)
t
i
S
T
S
i
J
2
ñc
2tx
2
2
==
&
()
tTS
iT
S
i
J
ñc
1ñc
1tx
1
1−
==
&
(6-11)
t
Tñc
+ iö
Tñc - t - iö
Tñc/2
i
60
ø
Maø α1 = α2 neân J1 = J2 = const. coù nghóa laø maät ñoä doøng ñieän phaân boá döôùi phaàn
tieáp xuùc cuûa choåi than gioáng nhau.
Khi choåi than rôøi khoûi phieán goùp 1 töùc laø i = – iö maø i1 = iö + i neân i1 = 0
Do vaäy khi rôøi khoûi phieán 1 khoâng phaùt sinh tia löûa treân choåi than.
2. Doøng ñieän ñoåi chieàu ñöôøng cong :
Treân thöïc teá eñc + epk ≠ 0 coù nghóa laø Σe ≠ 0 cho neân trong phaàn töû ñoåi chieàu
seõ xuaát hieän doøng ñieän ñoåi chieàu phuï xaùc ñònh theo soá haïng thöù 2 cuûa bieåu thöùc
(6-9) luùc naøy i = ic + if khieán cho quan heä i = f(t) khoâng coøn laø ñöôøng thaúng nöõa, ta
coù ñoåi chieàu ñöôøng cong.
a. Neáu epk > eñc hay Σe > 0: giaû söû rtx = const. töø bieåu thöùc (6-9) ta thaáy:
Trong ñoù:
Hình 6.5 Ñöôøng cong 1: Rtx = f(t)
Ñöôøng cong 2: if = f (i) khi Σe > 0
Ñöôøng cong 3: if = f (i) khi Σe < 0
Rtx : Laø ñieän trôû tieáp xuùc cuûa choåi than ñoái vôùi doøng
ñieän ñoåi chieàu phuï if ôû töøng thôøi ñieåm. Khi t = 0 vaø t
= Tñc thì Rtx = vaø khi thì Rtx = 4rtx.
Ñöôøng bieåu dieãn Rtx = f(t) laø ñöôøng 1 treân hình 6.5.
Neáu Σe = Cte vaø Σe > 0 thì if bieán ñoåi
theo ñöôøng cong 2 hình 6.5 vaø doøng ñieän ñoåi chieàu
i = ic + if bieán ñoåi theo ñöôøng cong treân h6-6.
ÔÛ tröôøng hôïp naøy ñoåi chieàu mang tính chaát
trì hoaõn, nghóa laø doøng ñieän i thay ñoåi chaäm hôn so
vôùi ñoåi chieàu ñöôøng thaúng.
Taïi t = 2
Tñc thì i ≠ 0
Taïi t > 2
Tñc thì i = 0
Sôû dó coù söï trì hoaõn ñoù laø do taùc duïng cuûa epk
choáng laïi söï bieán ñoåi cuûa doøng ñieän i. Töø h 6-6 ta
thaáy α1 > α2 vaø J1 > J2 maät ñoä doøng ñieän ñaàu ra lôùn
hôn ñaàu vaøo laøm tia löûa xuaát hieän ôû ñaàu ra cuûa choåi
than.
tx
ñc
ñcñc
tx
f
R
e
tT
T
t
T
r
e
i
∑∑
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
+
=
2
T
t
ñc
=
∞
1(Rtx)
Rtx, rf
2 if=f(t) khi Σe>0
3 if=f(t) khi Σe<0
Hình 6.6 Ñoåi chieàu chaäm sau(Σe > 0)
+ iö
- iö
Tñc - t
i
t
t
i
0