
H TH NG KI N TH C V CĂN B C HAI L P 9Ệ Ố Ế Ứ Ề Ậ Ớ
A - Căn b c haiậ
1. Đnh nghĩa: ịCăn b c hai c a s a không âm là s x sao cho xậ ủ ố ố 2 = a.
2. Ký hi u: ệ
a > 0:
a
: Căn b c hai c a s aậ ủ ố
−
a
: Căn b c hai âm c a s aậ ủ ố
a = 0:
=
0 0
3. Chú ý: V i a ớ
0:
= − =
2 2
( a ) ( a ) a
4. Căn b c hai s h c:ậ ố ọ
V i a ớ
0: s ố
a
đc g i là CBHSH c a aượ ọ ủ
Phép khi ph ng là phép toán tìm CBHSH c a s a không âm.ươ ủ ố
5. So sánh các CBHSH: V i a ớ
0, b
0:
�
a b a b
1.1 Đi n vào ô tr ng trong b ng sau:ề ố ả
x 11 12 13 14 15 16 17 18 19 20
x2
1.2 Tìm căn b c hai s h c r i suy ra căn b c hai c a các s sau:ậ ố ọ ồ ậ ủ ố
a) 121 b) 144 c) 169 d) 225
e) 256 f) 324 g) 361 h) 400
i) 0,01 j) 0,04 k) 0,49 l) 0,64
m) 0,25 n) 0,81 o) 0,09 p) 0,16
1.3 Tính:
1

a)
0,09
b)
16
−
c)
0,25. 0,16
d)
( 4).( 25)
− −
e)
25
4
f)
0405
166
,
g)
490360 ,,
1.4 Trong các s sau, s nào có căn b c hai:ố ố ậ
a)
5
b) 1,5 c) 0,1 d)
9
1.5 Trong các bi u th c sau, bi u th c nào có căn b c hai:ể ứ ể ứ ậ
a) (x – 4)(x – 6) + 1 b) (3 – x)(x – 5) – 4
c) x2 + 6x – 9 d) 5x2 + 8x – 4
e) x(x – 1)(x + 1)(x + 2) + 1 f) x2 + 20x + 101
1.6 So sánh hai s sau (không dùng máy tính):ố
a) 1 và
2
b) 2 và
3
c) 6 và
41
d) 7 và
47
e) 2 và
12
f) 1 và
3
1
g) 2
31
và 10 h)
3
và 12 i) 5 và
29
j) 2
5
và
19
k)
3
và
2
l)
32
và
23
m) 2 +
6
và 5 n) 7 – 2
2
và 4 o)
15
+
8
và 7
p)
1437
và 6–
15
q)
12617
và
99
1.7 Dùng kí hi u ệvi t nghi m c a các ph ng trình đi đây, sau đó dùng máyế ệ ủ ươ ướ
tính đ tính chính xác nghi m v i 3 ch s th p phân.ể ệ ớ ữ ố ậ
a) x2 = 2 b) x2 = 3 c) x2 = 3,5 d) x2 = 4,12
e) x2 = 5 f) x2 = 6 g) x2 = 2,5 h) x2 =
5
2

1.8 Gi i các ph ng trình sau:ả ươ
a) x2 = 25 b) x2 = 30,25 c) x2 = 5
d) x2 –
3
=
2
e) x2 5 = 0 f) x2 +
5
= 2
g) x2 =
3
h) 2x2+3
2
=2
3
i) (x – 1)2 = 1
9
16
j) x2 = (1 –
3
)2k) x2 = 27 – 10
2
l) x2 + 2x =3 –2
3
1.9 Gi i ph ng trình:ả ươ
a)
x
= 3 b)
x
=
5
c)
x
= 0 d)
x
= 2
1.10 Trong các s : ố
2
7)(
,
2
7)(
,
2
7
,
2
7)(
thì s nào là căn b c hai s h c c aố ậ ố ọ ủ
49 ?
1.11 Cho hai s d ng a và b. Ch ng minh r ng:ố ươ ứ ằ
a) N u a > b thì ế
ba
b) N u ế
ba
thì a > b
1.12 Cho s d ng a. Ch ng minh r ng:ố ươ ứ ằ
a) N u a > 1 thìế
a
> 1 b) N u a < 1 thì ế
a
< 1
1.13 Cho s d ng a. Ch ng minh r ng:ố ươ ứ ằ
a) N u a > 1 thì a > ế
a
b) N u a < 1 thì a < ế
a
3
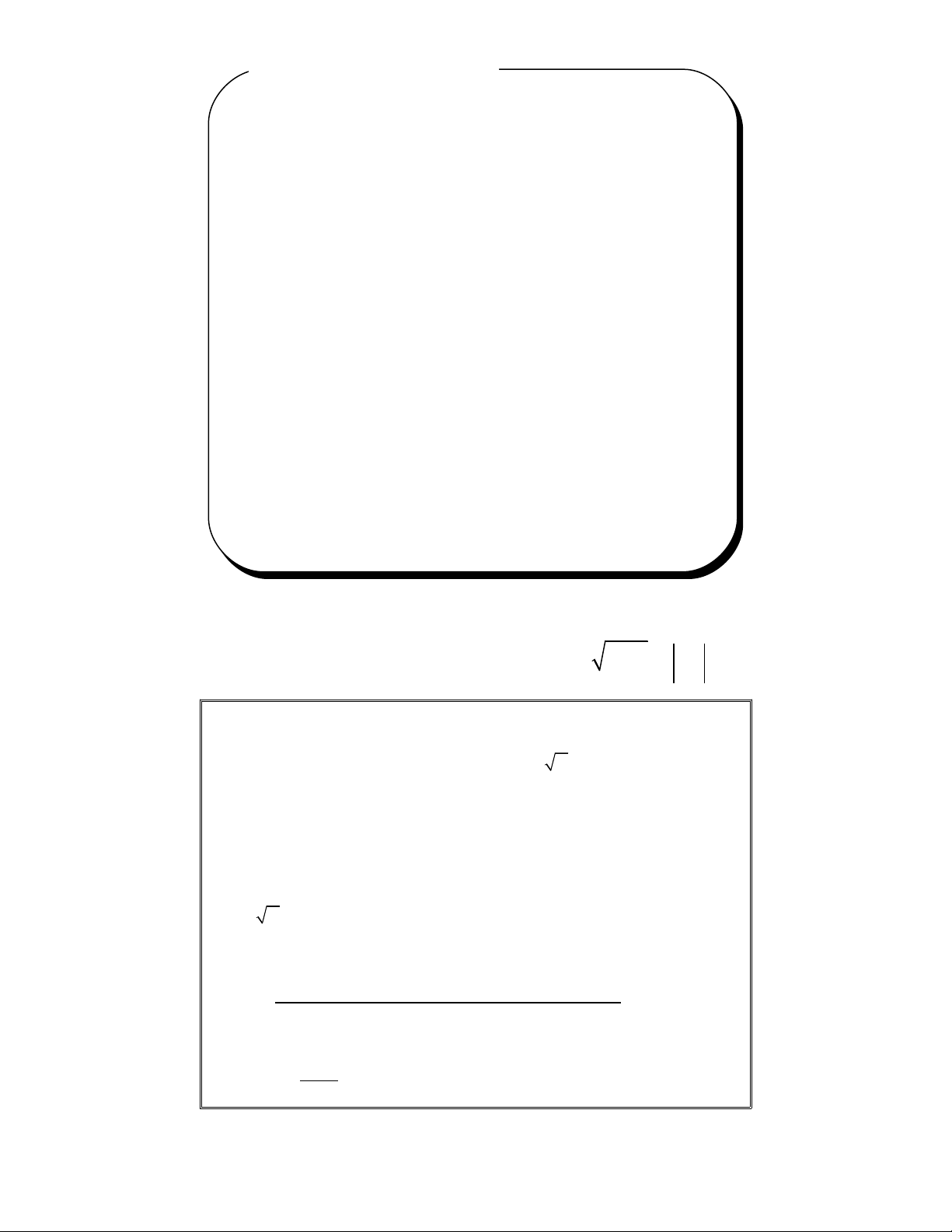
B - Căn th c b c hai. H ng đng th c ứ ậ ằ ẳ ứ
=
2
A A
1. Căn th c b c hai:ứ ậ
N u A là m t bi u th c đi s thì ế ộ ể ứ ạ ố
A
g i là căn th c b cọ ứ ậ
hai c a A. ủ
A đc g i là ượ ọ bi u th c l y cănể ứ ấ hay bi u th c d iể ứ ướ
d uấ căn.
A
các đnh (có nghĩa) khi A ị
0
Chú ý:
a) Đi u ki n có nghĩa c a m t s bi u th cề ệ ủ ộ ố ể ứ :
A(x) là m t đa th c ộ ứ
A(x) luôn có nghĩa.
A( x )
B( x )
có nghĩa
B(x)
0
4
(c ng 2 v v i c)ộ ế ớ
(c ng 2 v v i – c)ộ ế ớ
(c ng 2 v v i – b)ộ ế ớ
(c ng 2 v v i – b)ộ ế ớ
(n u c > 0: gi nguyên chi u)ế ữ ề
(n u c < 0: đi chi u)ế ổ ề
M t s tính ch t b t đng th cộ ố ấ ấ ẳ ứ

A( x )
có nghĩa
A(x)
0
1
A( x )
có nghĩa
A(x) > 0
b) V i M > 0, ta cóớ :
2 2
X M X M M X M
−��� �
2 2
X M X M X M
−�۳
ho c ặ
X M
2. H ng đng th c ằ ẳ ứ
2
( A ) A
=
Đnh lí: ịV i m i s a, ta có: ớ ọ ố
= = − <
2
a khi a 0
a a a khi a 0
Chú ý: T ng quát, v i A là m t bi u th c đi s , ta cũngổ ớ ộ ể ứ ạ ố
có:
= = − <
2
A khi A 0
A A A khi A 0
1.14 Tìm x đ bi u th c sau có nghĩa:ể ể ứ
1. a)
3x2
b)
x5
c)
7x3
d)
7x3
e)
3
x
f)
x5
g)
x4
h)
2
x1
i)
6x
5
2
j)
2
x
2
k)
x1
1
l)
3x
4
m)
2
x4
n)
2
x3
o)
1x2x
2
P)
2
x 2x 1
− − −
2. a)
5x4x
2
b)
2
x 2x 2
+ +
5


























