Hình học lớp 9 - ÔN TẬP CHƯƠNG II
(tiếp theo)
I. MỤC TIÊU
– Củng cố kiến thức về các dạng bài tập tổng
hợp về kiến thức hình học.
– Rèn luyện kỹ năng vẽ hình, phân tích, chứng
minh thông qua một số bài tập.
II. CHUẨN BỊ
* Giáo viên: Giáo án, SGK, phấn, thước thẳng,
compa.
* Học sinh: Chuẩn bị bài và dụng cụ học tập.
III. TIẾN TRÌNH LÊN LỚP
1. Ổn định tổ chức: Kiểm tra sĩ số
2. Bài cũ:
3. Bài ôn tập
Hoạt động Nội dung
GV: Cho đề bài toán
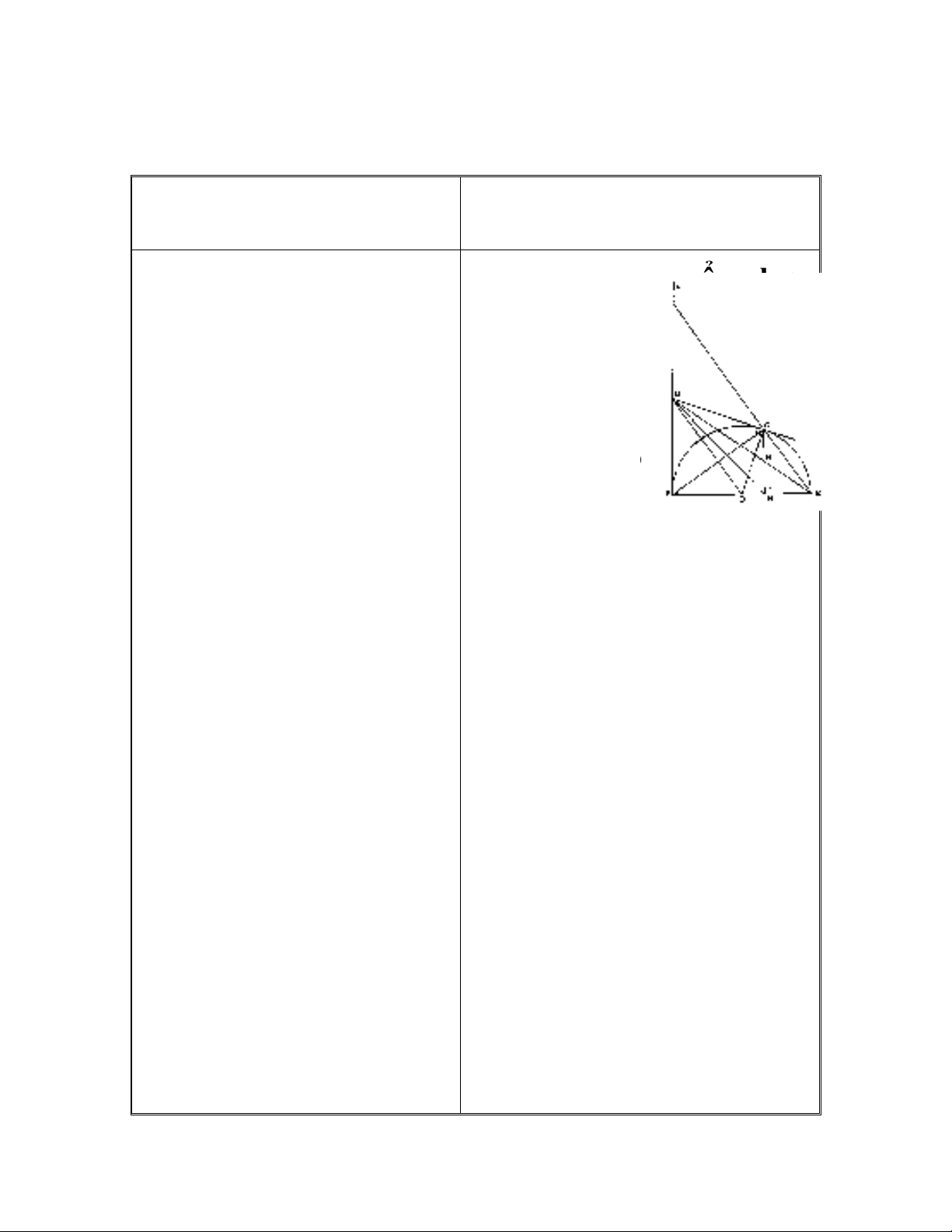
Bài 1: Cho nửa đường
tròn tâm O, đường kính
AB và tia tiếp tuyến Ax
cùng phía với nửa đường
tròn đối với AB. Từ
điểm M trên Ax (M khác
A), kẻ tiếp tuyến thứ hai
MC với nửa đường tròn
(C là tiếp điểm). Kẻ CH
vuông góc với AB (H
AB). Chứng minh rằng:
a)
·
0
90
ACB ;
b) BC // OM;
c) MB đi qua trung
Một số bài toán t
ổng hợp
cơ bản
Hướng dẫn
a) ABC có cạnh
AB là đường kính
của đường tròn
ngoại tiếp nên tam
giác ABC vuông tại
C, do đó
·
0
90
ACB
b) Có MA = MC
(Tính chất hai tiếp
tuy
ến cắt nhau) suy ra
MAC cân tại M,
mà MO là phân giác c
ủa
điểm của đoạn thẳng
CH.
GV: Hướng dẫn HS các
bước xây dựng cách giải
GV: Cho HS lên bảng
trình bày cách thực hiện.
·
AMC
(Tính ch
ất hai tiếp
tuyến cắt nhau), n
ên MO
cũng là đư
ờng cao của
MAC. Do đó MO AC,
lại có BC AC (
ABC
tại C) vậy BC // OM
c) Gọi I là giao đi
ểm của
BC với Ax v
à N là giao
điểm MB với CH.
Trong
ABI có:
OA = OB (bán kính) ; OM
// BI (vì OM // BC, I
BC)
suy ra MA = MI (1)
Mà CH // AI ( cùng vuông
góc với AB), do đó:
NH BN
MA BM
và
NC BN
MI BM
( H
ệ quả
định lí Ta -le
t) suy ra
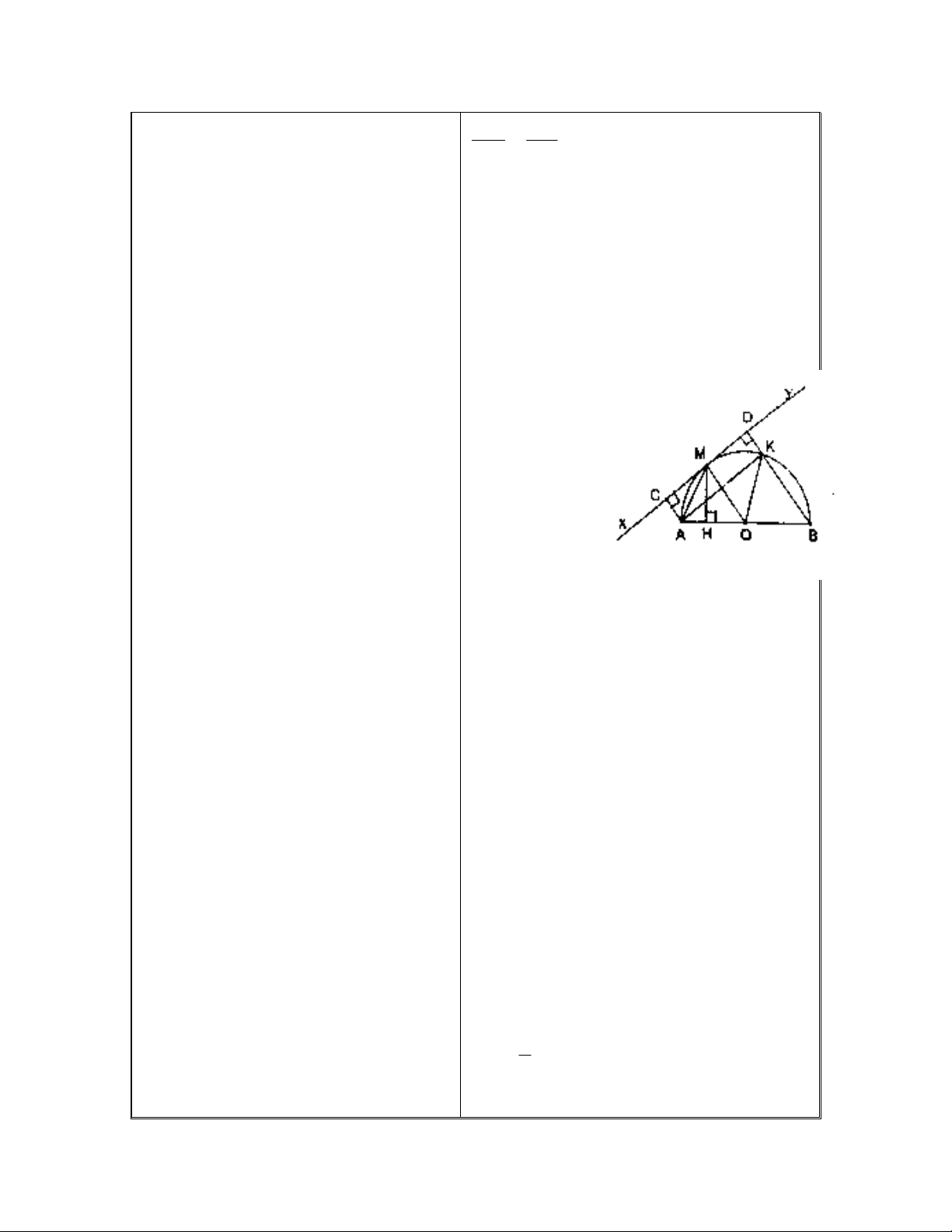
Bài 2: Cho nửa đường
tròn tâm O, dường kính
AB. Kẻ bán kính OM
sao cho góc AOM là góc
nhọn. Qua M, kẻ tiếp
tuyến xy với nửa đường
tròn. Kẻ AC vuông góc
với xy tại C, BD vuông
góc với xy tị D, cắt nửa
đường tròn tại K (K
khác B). Nối OK. Chứng
minh:
a)
·
·
OKB OBK
;
b) AK // xy;
c) AB là tiếp tuyến
của đường tròn đường
NH NC
MA MI
(2)
Từ (1) v
à (2) suy ra: NH =
NC hay BM đi qua trung
điểm của đoạn thẳng CH
Hướng dẫn
a) OK =AB
(bán kính)
Nên OKB
cân tại O
suy ra:
·
·
OKB OBK
b) Ta có O là
trung điểm của AB (v
ì AB
lsf đư
ờng kính của nửa
đường tr
òn tâm O), nên
1
2
OB AB
, mà OK=OB(bán
kính CD.
kính). Suy ra
1
2
OK AB
vậy AKB vuông t
ạiK,
suy ra AK BD.
Ta lại có BD xy (gi
ả
thiết)
Do đó AK // xy.
c) Kẻ MH AB t
ại H, nối
AM. Tacó OM
xy (là
tiếp tuyến của đường tr
òn
(O)) mà AC xy, BD
xy nên AC // OM // BD. Ta
lại co O là trung đi
ểm của
AB (AB là đư
ờng kính của
đường tr
òn (O)). Suy ra M
là trung đi
ểm của CD (AC,
OM, BD là ba đư
ờng thẳng
song song cách đ
ều) hay M