Tạp chí Khoa học Giao thông vận tải, Tập 72, Số 08 (10/2021), 945-956
945
Transport and Communications Science Journal
SELECTION STUDY OF STATE VARIABLES
IN ACTIVE CONTROL OF SUSPENSION SYSTEMS
USING HEDGE ALGEBRAS THEORY
Hai Le Bui1*, Dang Khoa Do1, Anh Tuan Le2
1Hanoi University of Science and Technology, No 1 Dai Co Viet Street, Hanoi, Vietnam
2Song Hong Technology & Science Joint Stock Company, No 28/39/7 Dai Dong Street,
Hanoi, Vietnam
ARTICLE INFO
TYPE: Research Article
Received: 25/07/2021
Revised: 30/08/2021
Accepted: 14/09/2021
Published online: 15/10/2021
https://doi.org/10.47869/tcsj.72.8.8
* Corresponding author
Email: le.buihai@hust.edu.vn; Tel: +84 913574956
Abstract. Research on vibration control of vehicle active and semi-active suspension systems
is increasingly interested. In the present work, the investigation of the state variables selection
to find the control variable in the hedge-algebras-based controller is carried out for a quarter
car active suspension model. State variables that can be used include vertical displacement,
velocity, and acceleration of the vehicle body and wheel. By investigating the influence of
state variables on the efficiency of the hedge-algebras-based controller consisting of two input
state variables and one output control variable, it is possible to determine the appropriate state
variables for the control targets. The numerical simulation results show that the controller is
most effective when using the vehicle's body speed and acceleration as state variables. The
present approach can be extended to different controlled objects to find suitable state
variables, especially for controllers using qualitative rule systems such as controllers based on
the fuzzy-set or hedge-algebras theories.
Keywords: vehicle suspension systems, vibration control, state variables selection, hedge-
algebras theory.
©
2021 University of Transport and Communications
Transport and Communications Science Journal, Vol 72, Issue8 (10/2021), 945-956
946
Tạp chí Khoa học Giao thông vận tải
KHẢO SÁT SỰ LỰA CHỌN BIẾN TRẠNG THÁI
TRONG ĐIỀU KHIỂN HỆ THỐNG TREO CHỦ ĐỘNG
SỬ DỤNG LÝ THUYẾT ĐẠI SỐ GIA TỬ
Bùi Hải Lê1*, Đỗ Đăng Khoa1, Lê Anh Tuấn2
1Trường Đại học Bách Khoa Hà Nội, Số 1 Đại Cồ Việt, Hà Nội, Việt Nam
2Công ty Cổ phần Khoa học và Công nghệ Sông Hồng, Số 28/39/7 Đại Đồng, Hà Nội, Việt
Nam
THÔNG TIN BÀI BÁO
CHUYÊN MỤC: Công trình khoa học
Ngày nhận bài: 25/07/2021
Ngày nhận bài sửa: 30/08/2021
Ngày chấp nhận đăng: 14/09/2021
Ngày xuất bản Online: 15/10/2021
https://doi.org/10.47869/tcsj.72.8.8
* Tác giả liên hệ
Email: le.buihai@hust.edu.vn; Tel: +84 913574956
Tóm tắt. Nghiên cứu về điều khiển dao động của các hệ thống treo chủ động và bán chủ động
trên xe ô tô ngày càng được quan tâm. Trong bài báo này, việc khảo sát về sự lựa chọn các
biến trạng thái để tìm biến điều khiển trong bộ điều khiển dựa trên lý thuyết đại số gia tử được
thực hiện cho một hệ thống treo chủ động của mô hình một phần tư xe ô tô. Các biến trạng
thái có thể được sử dụng bao gồm chuyển vị, vận tốc và gia tốc theo phương thẳng đứng của
thân xe và bánh xe. Bằng việc khảo sát ảnh hưởng của các biến trạng thái đến hiệu quả của bộ
điều khiển dựa trên đại số gia tử gồm 2 biến trạng thái đầu vào và 1 biến điều khiển đầu ra
cho phép xác định được các biến trạng thái phù hợp với các mục tiêu điều khiển. Kết quả mô
phỏng số cho thấy bộ điều khiển đạt hiệu quả cao nhất khi sử dụng vận tốc và gia tốc của thân
xe làm biến trạng thái. Cách tiếp cận của bài báo có thể được mở rộng cho những đối tượng
được điều khiển khác nhau để tìm ra các biến trạng thái phù hợp, nhất là đối với những bộ
điều khiển sử dụng hệ luật định tính như các bộ điều khiển dựa trên lý thuyết tập mờ hay đại
số gia tử.
Từ khóa: hệ thống treo của xe ô tô, điều khiển dao động, lựa chọn biến trạng thái, đại số gia
tử.
©
2021 Trường Đại học Giao thông vận tải
Tạp chí Khoa học Giao thông vận tải, Tập 72, Số 08 (10/2021), 945-956
947
1. ĐẶT VẤN ĐỀ
Với yêu cầu ngày càng cao đối với vận hành của ô tô, hệ thống treo trên xe có vai trò
quan trọng trong điều khiển xe, tạo sự thoải mái cho hành khách và cách ly xe khỏi tiếng ồn,
va chạm, rung lắc trên đường,...
Trên quan điểm của chế độ điều khiển, hệ thống treo của xe có thể được phân thành ba
loại: bị động, bán chủ động và chủ động. Trong các loại trên, hệ thống treo chủ động có tiềm
năng lớn nhất để cải thiện sự thoải mái khi lái xe và khả năng vận hành của phương tiện, và
lĩnh vực nghiên cứu này vẫn nhận được sự quan tâm trong nhiều năm qua. Trong hệ thống
treo chủ động, các cơ cấu sinh lực được đặt giữa thân xe và trục bánh xe song song với các bộ
phận của phần tử treo, vừa có thể bổ sung và tiêu hao năng lượng từ hệ thống, giúp hệ thống
treo kiểm soát được ứng xử của xe, tăng sự thoải mái khi lái xe và khả năng bám đường của
xe. Mặc dù điều khiển chủ động có nhiều ưu điểm, nhưng cũng có một số hạn chế gồm: (1)
thuật toán điều khiển phức tạp; (2) rủi ro tiềm ẩn về độ tin cậy; và (3) tiêu thụ thêm năng
lượng [1].
Nhiều các thuật toán điều khiển hiện đại và thông minh đã được áp dụng cho bài toán này
[2-9]. Trong phương pháp điều khiển thông minh, điều khiển mờ chiếm số lượng đáng kể với
những ưu điểm như đơn giản, hiệu quả và sử dụng ít biến trạng thái [10-12].
Với cách tiếp cận khác với cách tiếp cận trong lý thuyết tập mờ, lý thuyết đại số gia tử
(Hedge-algebras, HA) cho phép biểu diễn các biến ngôn ngữ bằng các độ đo mờ định lượng
của chúng (các số thực trong khoảng từ 0 đến 1) dựa trên thứ tự ngữ nghĩa tự nhiên của các
giá trị ngôn ngữ mà không cần sử dụng các hàm liên thuộc mờ [13, 14]. Do đó, lý thuyết HA
đã phát triển và đạt được kết quả khả quan trong một số lĩnh vực, liên quan đến các vấn đề cơ
sở dữ liệu, lập trình logic, phân lớp và hồi quy, dự báo với chuỗi thời gian mờ và tóm tắt ngôn
ngữ.
Trong lĩnh vực điều khiển dao động kết cấu hay điều khiển cân bằng của các hệ hụt dẫn
động, bộ điều khiển dựa trên đại số gia tử cho thấy nhiều lợi thế so với bộ điều khiển dựa trên
tập mờ, chẳng hạn như đơn giản hơn trong thiết kế và tối ưu hóa, hiệu quả điều khiển cao hơn
và thời gian tính toán nhanh hơn nhiều [15-23].
Tuy nhiên, trong các nghiên cứu kể trên, các khảo sát lựa chọn được các biến trạng thái
phù hợp cho bộ điều khiển dựa trên HA chưa được thực hiện. Vì vậy, trong nghiên cứu này,
hiệu quả của các bộ điều khiển dựa trên HA, gồm 2 biến trạng thái đầu vào và 1 biến điều
khiển đầu ra, được đánh giá thông qua các cặp biến trạng thái khác nhau để tìm ra cặp biến
trạng thái phù hợp nhất với đối tượng được điều khiển – hệ thống treo chủ động của mô hình
một phần tư xe ô tô.
2. HỆ THỐNG TREO CHỦ ĐỘNG
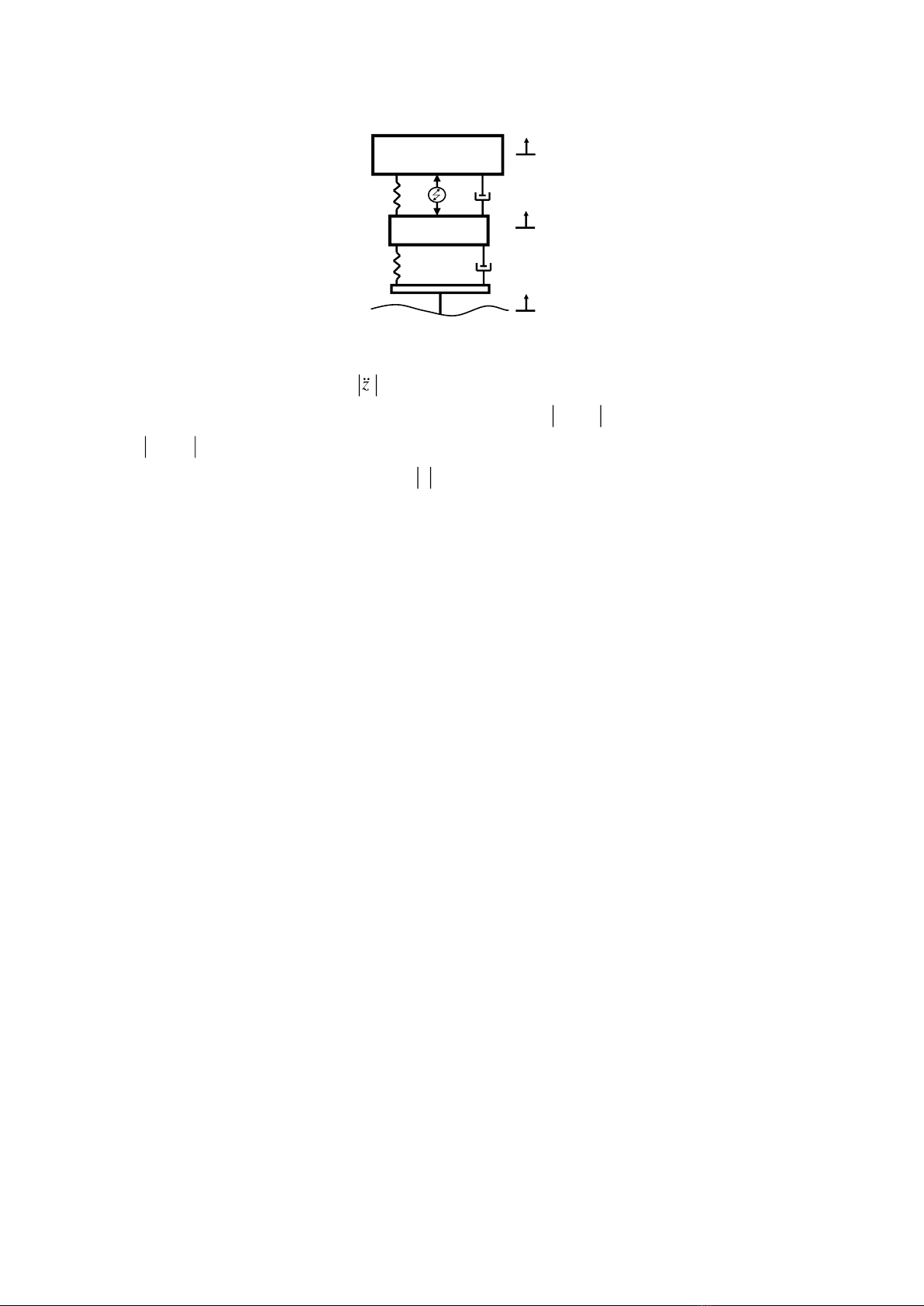
Xét hệ thống treo chủ động của mô hình một phần tư xe ô tô như Hình 1. Trong đó, m1 và
m2 là khối lượng của thân xe và bánh xe; k1, k2, c1, c2 lần lượt là độ cứng và hệ số cản của hệ
thống treo và lốp xe; z1, z2, zr lần lượt chuyển vị của thân xe, của lốp và biên dạng mặt đường.
Lực điều khiển u được sinh ra từ máy kích động đặt vào giữa các khối lượng m1 và m2. Hệ
phương trình trạng thái của hệ được viết dưới dạng ma trận như sau [1]:
1 1 1 1 1 1 1 1
2 2 1 1 2 2 1 1 2 2 2 2
00
0rr
m z c c z k k z u
m z c c c z k k k z c z k z u
−−

+ + = +
− + − + + −

(1)
Transport and Communications Science Journal, Vol 72, Issue8 (10/2021), 945-956
948
u
c2
c1
k1
k2
m1
m2
z1
z2
zr
Hình 1. Hệ thống treo chủ động của mô hình một phần tư xe ô tô.
Các vấn đề cần giải quyết đối với hệ thống treo kể trên bao gồm [24]: (1) Giá trị tuyệt đối
cực đại của gia tốc thân xe max
1
z
, đại lượng này cần giảm thiểu để đảm bảo sự thoải mái
cho hành khách; (2) Biến dạng của bộ phận treo max
12
zz−
và biến dạng của lốp xe
max
2r
zz−
, các đại lượng này cũng cần giảm thiểu để đảm bảo an toàn của hệ thống; (3)
Giới hạn vật lý của máy kích động max
max
uu
, trong đó umax lực điều khiển cho phép của
máy kích động; (4) Thời gian dao động của hệ thống cần được giảm thiểu.
3. THIẾT KẾ BỘ ĐIỀU KHIỂN
Xét một cấu trúc đại số gia tử của biến ngôn ngữ X như sau:
( )
, , , ,AX X G C H=
(2)
trong đó G, C, và H lần lượt là các nhãn ngôn ngữ gốc, các hằng số và các gia tử. Dấu “” thể
hiện quan hệ thứ tự của X.
Thông thường, lý thuyết HA cho phép xác định tất cả các giá trị ngôn ngữ của biến ngôn
ngữ X bằng cách kết hợp 2 nhãn ngôn ngữ gốc Âm và Dương (ký hiệu là A và D); 3 hằng số 0
(tuyệt đối Âm), W (trung hòa) và 1 (tuyệt đối Dương); và 2 gia tử Hơi và Rất (ký hiệu là H và
R) như sau:
, A, D
0, W, 1
, H, R
G c c
C
H h h
−+
−+
==
=
==
(3)
Trong lý thuyết HA, các giá trị ngôn ngữ được biểu diễn bởi các giá trị độ đo tính mờ của
chúng trong khoảng
0,1
, và vì vậy, các thao tác đối với các giá trị ngôn ngữ được thực hiện
trên các số thực thay vì sử dụng các tập mờ như trong lý thuyết tập mờ. Các công thức để xác
định một giá trị độ đo tính mờ, còn gọi là giá trị ánh xạ ngữ nghĩa định lượng (semantically
quantifying mapping, SQM), đã được tóm tắt trong [18]. Một số giá trị SQM
của các giá trị
ngôn ngữ điển hình được thể hiện trên Hình 2 với trường hợp fm(c-) =
(h-) = 0,5 (mô hình
hóa đối xứng). Trong đó, fm(c-) và
(h-) lần lượt là độ đo tính mờ của c- và h-.
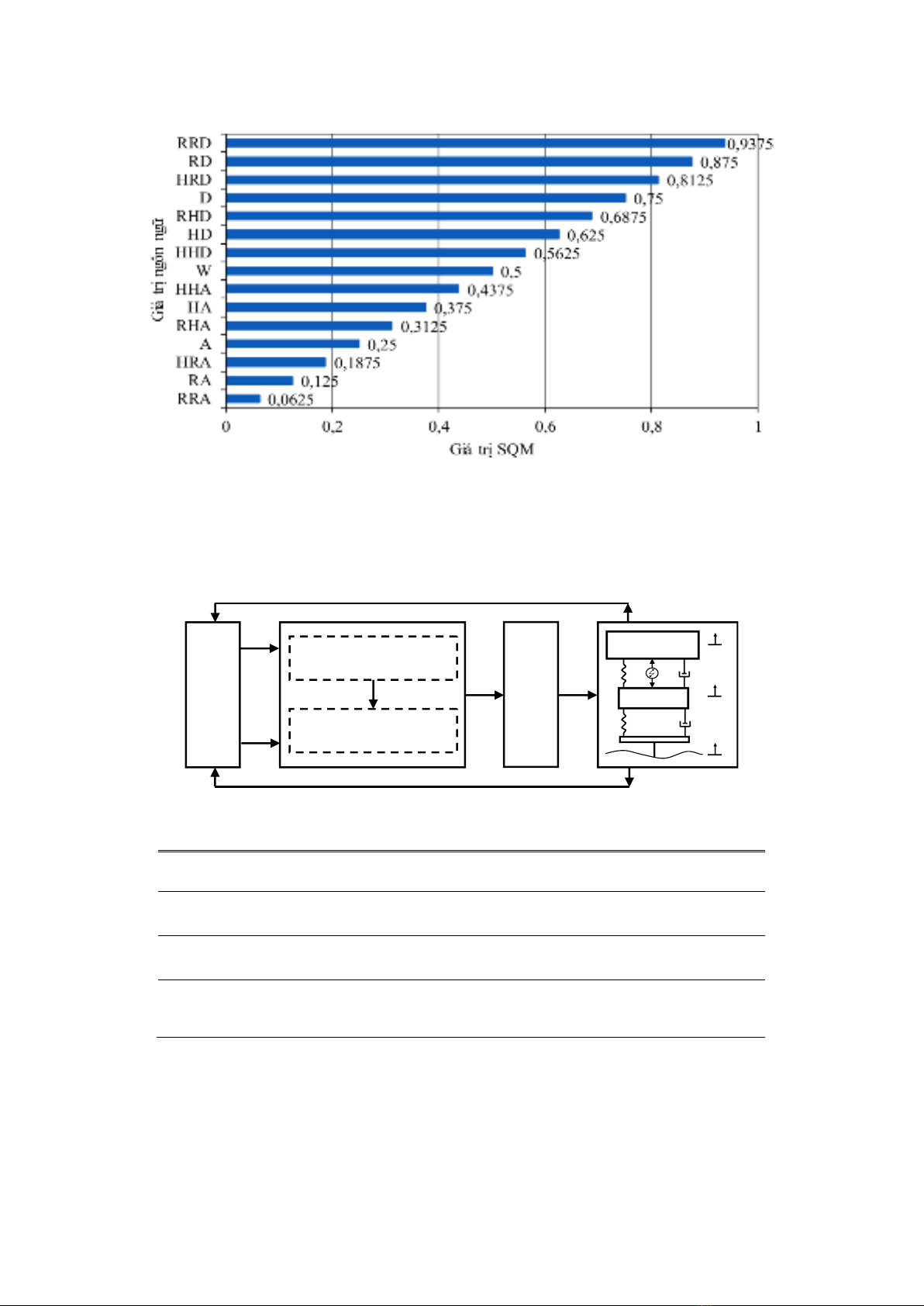
Từ Hình 2, có thể thấy mối quan hệ giữa các giá trị ngôn ngữ và giá trị SQM của chúng là
đồng biến, nghĩa là lý thuyết HA đảm bảo thứ tự ngữ nghĩa tự nhiên của các giá trị ngôn ngữ
của một biến ngôn ngữ.
Tạp chí Khoa học Giao thông vận tải, Tập 72, Số 08 (10/2021), 945-956
949
Hình 2. Giá trị SQM của một số giá trị ngôn ngữ điển hình.
Bộ điều khiển dựa trên HA gồm 2 biến trạng thái đầu vào, x1 và x2, và 1 biến điều khiển
đầu ra u. Trong đó, x1 và x2 được tổ hợp từ chuyển vị, vận tốc và gia tốc của thân xe và bánh
xe. Sơ đồ nguyên lý của bộ điều khiển được thể hiện trên Hình 3, trong đó x1S, x2S, và uS lần
lượt là giá trị SQM của z1, z2, và u. Các giá trị ngôn ngữ với giá trị SQM và khoảng xác định
của các biến trạng thái và biến điều khiển được lựa chọn và thể hiện trên Bảng 1.
u
c2
c1
k1
k2
m1
m2
z1
z2
zr
1
x
Chuẩn hóa
Cơ sở luật HA
Suy luận HA
u
2
x
us
x1s
x2s
Giải chuẩn
Hình 3. Sơ đồ nguyên lý của bộ điều khiển.
Bảng 1. Tham số của các biến.
Biến
Khoảng xác định
Các giá trị ngôn ngữ với giá trị SQM
x1
,aa−
A: 0,25 ; HA: 0,375 ; W: 0,5 ; HD: 0,625 ; D: 0,75
x2
,bb−
HA: 0,375 ; W: 0,5 ; HD: 0,625
u
,cc−
RA: 0,125; A: 0,25; HA: 0,375; W: 0,5;
HD: 0,625; D: 0,75; RD: 0,875
Các bước Chuẩn hóa và Giải chuẩn để chuyển đổi giữa các giá trị thực và giá trị SQM
của các biến, vì vậy các bước này tương đương với các bước Mờ hóa và Giải mờ của một bộ
điều khiển dựa trên lý thuyết tập mờ. Các bước Chuẩn hóa và Giải chuẩn được thể hiện trên
Hình 4 sử dụng các phép nội suy tuyến tính.