www.VNMATH.com
CHUYÊN Đ Ề
PH NG PHÁP T A Đ TRONG KHÔNG GIANƯƠ Ọ Ộ
I. PH NG PHÁP GI I TOÁNƯƠ Ả
Đ gi i đ c các bài toán hình không gian b ng ph ng pháp t a đ ta c n ph i ch n h tr c t a đ thíchể ả ượ ằ ươ ọ ộ ầ ả ọ ệ ụ ọ ộ
h p. L p t a đ các đ nh, đi m liên quan d a vào h tr c t a đ đã ch n và đ dài c nh c a hình.ợ ậ ọ ộ ỉ ể ự ệ ụ ọ ộ ọ ộ ạ ủ
PH NG PHÁP ƯƠ
B c 1:ướ Ch n h tr c t a đ Oọ ệ ụ ọ ộ xyz thích h p. (Quy t đ nh s thành công c a bài toán)ợ ế ị ự ủ
B c 2:ướ Xác đ nh t a đ các đi m có liên quan.ị ọ ộ ể
B c 3:ướ S d ng các ki n th c v t a đ đ gi i quy t bài toán.ử ụ ế ứ ề ọ ộ ể ả ế
Các d ng toán th ng g p:ạ ườ ặ
•Đ nh tính: Ch ng minh các quan h vuông góc, song song, …ị ứ ệ
•Đ nh l ng: Đ dài đo n th ng,, góc, kho ng cách, tính di n tích, th tích, di n tích thi t di n, …ị ượ ộ ạ ẳ ả ệ ể ệ ế ệ
•Bài toán c c tr , qu tích.ự ị ỹ
……………
Ta th ng g p các d ng sauườ ặ ạ
1. Hình chóp tam giác
a. D ng tam di n vuôngạ ệ
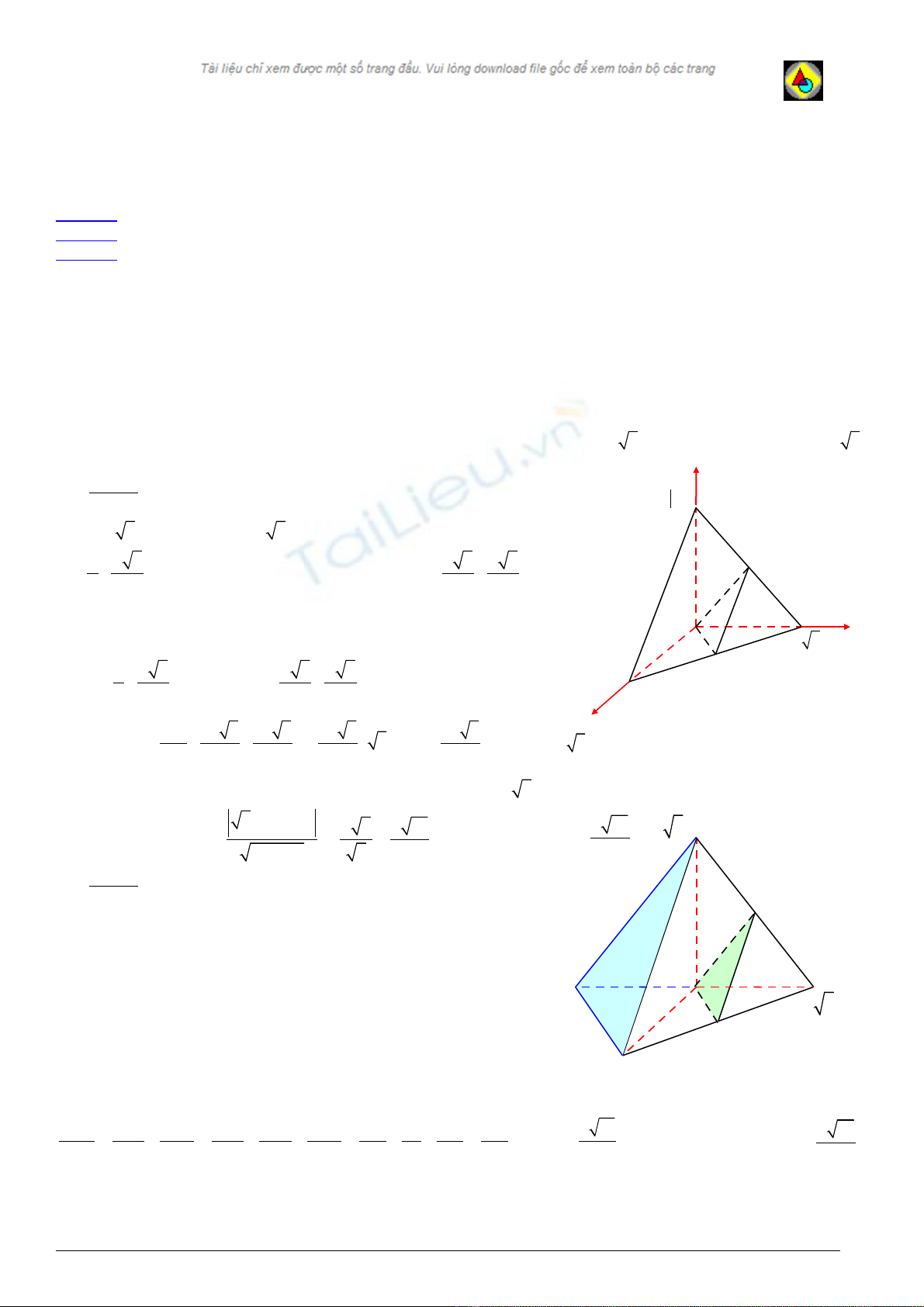
Ví d :ụ Cho t di n ứ ệ OABC có đáy OBC là tam giác vuông t i ạO, OB=a, OC=
3a
, (a>0) và đ ng cao ườ OA=
3a
.
G i ọM là trung đi m c a c nh ể ủ ạ BC. Tính kho ng cách gi a hai đ ng th ng ả ữ ườ ẳ AB và OM.
Cách 1:
Ch n h tr c t a đ nh hình v . Khi đó ọ ệ ụ ọ ộ ư ẽ O(0;0;0),
(0;0; 3); ( ;0;0), (0; 3; 0),A a B a C a
3
; ; 0
2 2
a a
M
÷
÷
, g i ọN là trung đi m c a ể ủ AC ⇒
3 3
0; ;
2 2
a a
N
÷
÷
.
MN là đ ng trung bình c a tam giác ườ ủ ABC ⇒ AB // MN
⇒ AB //(OMN) ⇒ d(AB;OM) = d(AB;(OMN)) = d(B;(OMN)).
3 3 3
; ; 0 , 0; ;
2 2 2 2
a a a a
OM ON
= =
÷ ÷
÷ ÷
uuuur uuur
( )
2 2 2 2 2
3 3 3 3 3
[ ; ] ; ; 3; 1; 1
4 4 4 4 4
a a a a a
OM ON n
= = =
÷
÷
uuuur uuur r
, v i ớ
( 3; 1; 1)n
=
r
.
Ph ng trình m t ph ng (ươ ặ ẳ OMN) qua O v i vect pháp tuy n ớ ơ ế
Ta có:
3. 0 0 3 15
( ; ( )) 5
3 1 1 5
aa a
d B OMN + +
= = =
+ +
. V y, ậ
15
( ; ) .
5
a
d AB OM =
Cách 2:
G i ọN là đi m đ i x ng c a ể ố ứ ủ C qua O.
Ta có: OM // BN (tính ch t đ ng trung bình).ấ ườ
⇒ OM // (ABN)
⇒ d(OM;AB) = d(OM;(ABN)) = d(O;(ABN)).
D ng ự
, ( ; )OK BN OH AK K BN H AK⊥ ⊥ ∈ ∈
Ta có:
( );AO OBC OK BN AK BN⊥ ⊥ ⇒ ⊥
; ( )BN OK BN AK BN AOK BN OH⊥ ⊥ ⇒ ⊥ ⇒ ⊥
; ( ) ( ; ( )OH AK OH BN OH ABN d O ABN OH⊥ ⊥ ⇒ ⊥ ⇒ =
T các tam giác vuông ừOAK; ONB có:
2 2 2 2 2 2 2 2 2 2
1 1 1 1 1 1 1 1 1 5 15
5
3 3 3
a
OH
OH OA OK OA OB ON a a a a
= + = + + = + + = ⇒ =
. V y, ậ
15
( ; ) .
5
a
d OM AB OH= =
b. D ng khácạ
Ví d 1:ụ T di n ứ ệ S.ABC có c nh ạSA vuông góc v i đáy và ớ
ABC∆
vuông t i ạC. Đ dài c a các c nh là ộ ủ ạ SA =4, AC =
3, BC = 1. G i ọM là trung đi m c a c nh ể ủ ạ AB, H là đi m đ i x ng c a ể ố ứ ủ C qua M.
Chuyên đ : ềPH NG PHÁP T A Đ TRONG KHÔNG GIAN ƯƠ Ọ Ộ www.VNMATH.com
1
z
A
3a
3a
y
C
N
O
M
a
x
B
O
A
3a
3a
C
N
M
a
B
GSP 4.06.exe
www.VNMATH.com
Tính cosin góc h p b i hai m t ph ng (ợ ở ặ ẳ SHB) và (SBC).
H ng d n gi iướ ẫ ả
Ch n h tr c t a đ nh hình v , ta có:ọ ệ ụ ọ ộ ư ẽ
A(0;0;0), B(1;3;0), C(0;3;0), S(0;0;4) và H(1;0;0).
mp(P) qua H vuông góc v i ớSB t i ạI c t đ ng th ng ắ ườ ẳ SC t i ạK, d th y ễ ấ
( ) ( )
·
( )
, , SHB SBC IH IK=uuur uur
(1).
( 1; 3; 4)SB = − −
uur
,
(0; 3; 4)SC = −
uuur
suy ra:
ptts SB:
1
3 3
4
x t
y t
z t
= −
= −
=
, SC:
0
3 3
4
x
y t
z t
=
= −
=
và (P): x + 3y – 4z – 1 = 0.
5 15 3 51 32
; ; , 0; ;
8 8 2 25 25
I K
⇒ ÷ ÷
( ) ( )
·
.
cos , .
IH IK
SHB SBC IH IK
⇒ =
uuur uur
= …
Chú ý: N u ếC và H đ i x ng qua ố ứ AB thì C thu c (ộP), khi đó ta không c n ph i tìm ầ ả K.
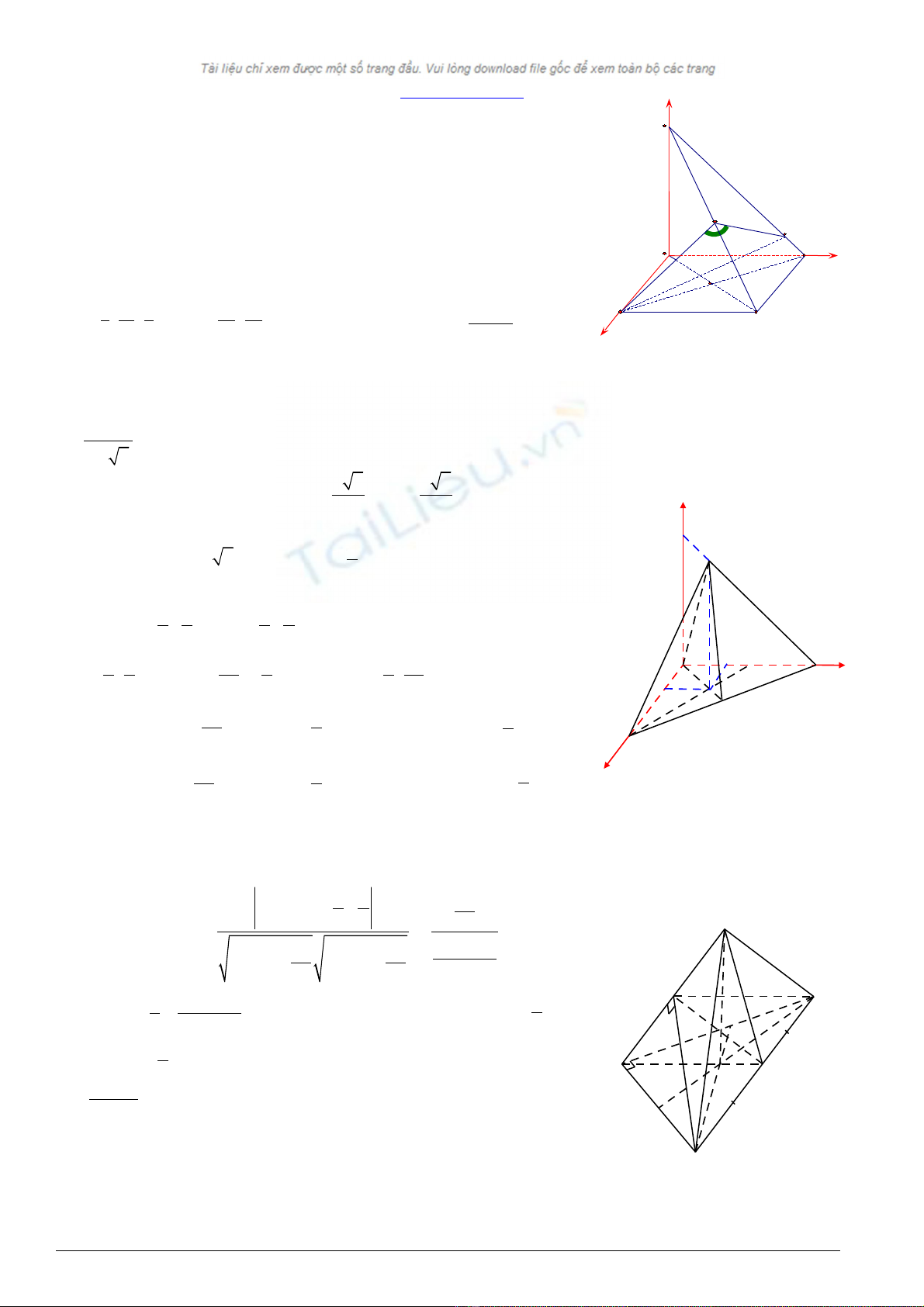
Ví d 2: ụCho hình chóp SABC có đáy là tam giác ABC vuông cân t i ạA, AB = AC = a (a > 0), hình chi u c a ế ủ S trên
đáy trùng v i tr ng tâm ớ ọ G c a ủ∆ABC. Đ t ặSG = x (x > 0). Xác đ nh giá tr c a ị ị ủ x đ góc ph ng nh di n (ể ẳ ị ệ B, SA, C)
b ng 60ằo.
Cách 1 :
2BC a=
G i ọM là trung đi m c a ể ủ BC
2 2
;
2 3
a a
AM AG⇒ = =
.
G i ọE, F l n l t là hình chi u c a ầ ượ ế ủ G lên AB, AC. T giác ứAEGF là hình vuông
2 .
3
a
AG AE AE AF⇒ = ⇒ = =
D ng h tr c t a đ ự ệ ụ ọ ộ Axyz, v i ớAx, Ay, Az đôi m t vuông góc, ộA(0;0;0), B(a;0;0),
C(0; a; 0),
; ; 0 , ; ;
3 3 2 2
a a a a
G S x
÷ ÷
.
2 2
; ; , ; ; , ; ;
3 3 3 3 3 3
a a a a a a
SA x SB x SC x
= = − − = − −
÷ ÷ ÷
uur uur uuur
2
1
[ ; ] 0; ; 0; ; .
3 3
a a
SA SB ax a x a n
= − = − =
÷ ÷
÷
uur uur r
, v i ớ
10; ; 3
a
n x
= −
÷
r
2
2
[ ; ] ( ; 0; ) ; 0; . ,
3 3
a a
SA SC ax a x a n
= − = − − = −
÷
uur uuur r
v i ớ
2; 0; 3
a
n x
= −
÷
r
.
M t ph ng (ặ ẳ SAB) có c p vect ch ph ng ặ ơ ỉ ươ
,SA SB
uur uur
nên có vect pháp tuy n ơ ế
1
n
r
.
M t ph ng (ặ ẳ SAC) có c p vect ch ph ng ặ ơ ỉ ươ
,SA SC
uur uuur
nên có vect pháp tuy n ơ ế
2
n
r
.
Góc ph ng nh di n (ẳ ị ệ B; SA; C) b ng 60ằo.
2
2 2
2 2
2 2
0. .0 3 3 9
cos 60
9
0 0 9
9 9
o
a a a
x x
x a
a a
x x
+ +
⇔ = = +
+ + + +
2
2 2
1
29
a
x a
⇔ = +
2 2 2 2 2
9 2 9 .
3
a
x a a x a x⇔ + = ⇔ = ⇔ =
V y, ậ
.
3
a
x=
Cách 2:
G i ọM là trung đi m c a ể ủ BC
AM BC⇒ ⊥
(∆ABC vuông cân)
Ta có:
( )SG ABC SG BC⊥ ⇒ ⊥
. Suy ra:
( )BC SAM⊥
D ng ự
BI SA IM SA⊥ ⇒ ⊥
và
IC SA⊥
·
BIC⇒
là góc ph ng nh di n (ẳ ị ệ B; SA; C).
( )SAB SAC c c c∆ = ∆ − −
IB IC IBC⇒ = ⇒ ∆
cân t iạ I.
Chuyên đ : ềPH NG PHÁP T A Đ TRONG KHÔNG GIAN ƯƠ Ọ Ộ www.VNMATH.com
2
GM
C
S
I
A
B
z
x
x
y
C
B
A
E
F
G
M
x
4
z
y
M
B
A
H
S
C
K
I
z
x
y
AD
D'
C'
B
B'
C
A'
www.VNMATH.com
1 2 2
2; ;
2 2 3
a a
BC a AM BM MC BC AG= = = = = =
.
2 2 2
2
2 1 2
~ . . .
22
29
AM a ax
AIM AGS IM SG x
AS SG AG a
x
∆ ∆ ⇒ = = =
++
2 2
3 2
2 9 2
ax
IM
x a
⇔ = +
.
Ta có:
·
60o
BIC =
·
2 2
2 3.3 2
30 .tan 30 22 9 2
o o a ax
BIM BM IM
x a
⇔ = ⇔ = ⇔ = +
.
2 2 2 2 2 2 2 2 2
9 2 3 3 9 2 27 18 2 9 .
3
a
x a x x a x x a x a x⇔ + = ⇔ + = ⇔ = ⇔ = ⇔ =
V y, ậ
.
3
a
x=
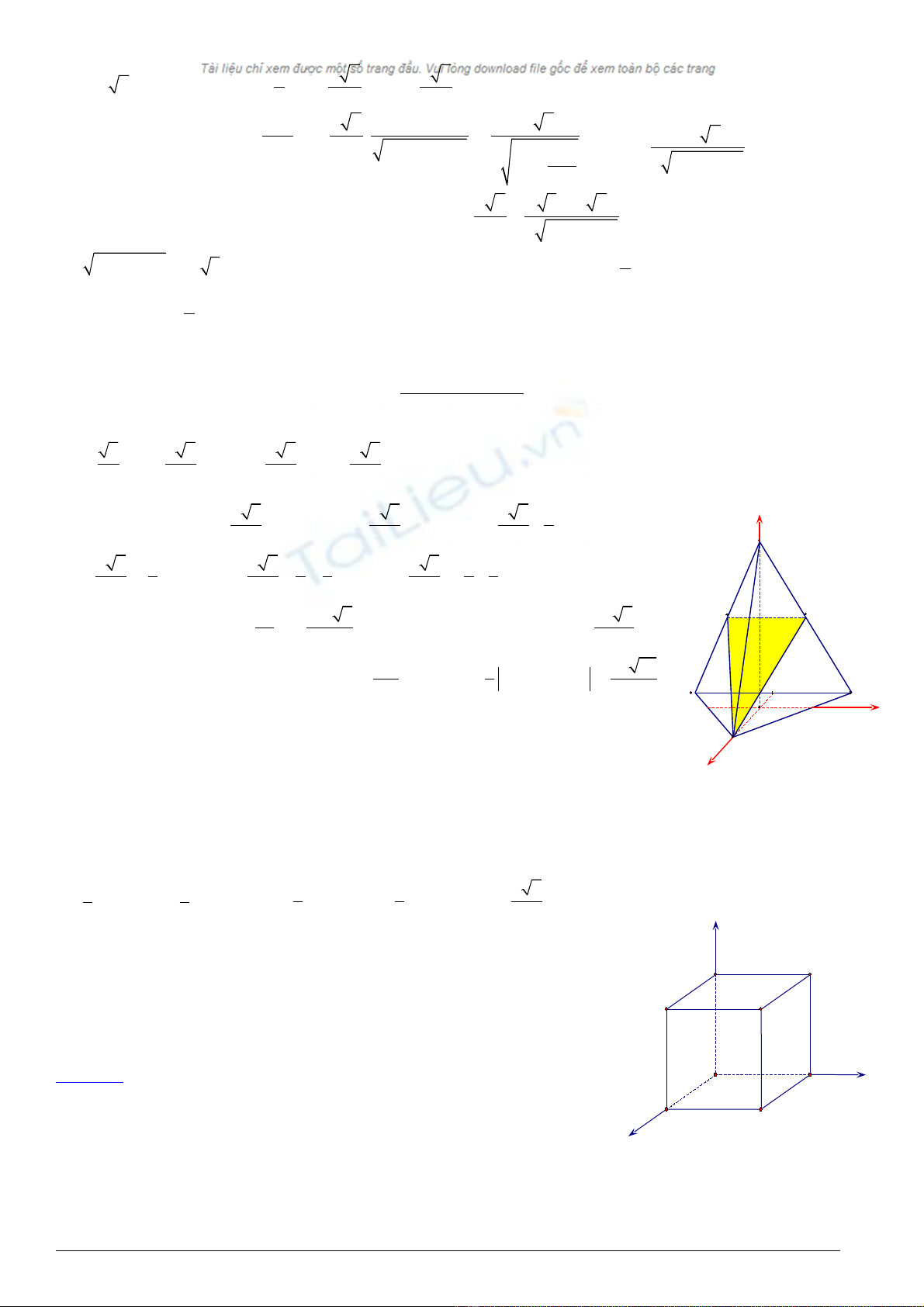
Ví d 3:ụ (Trích đ thi Đ i h c kh i A – 2002). Cho hình chóp tam giác đ u ề ạ ọ ố ề S.ABC có đ dài c nh đáy là ộ ạ a. G i ọM,
N là trung đi m ểSB, SC. Tính theo a di n tích ệ∆AMN, bi t (ếAMN) vuông góc v i (ớSBC).
H ng d n gi iướ ẫ ả
G i O là hình chi u c a S trên (ọ ế ủ ABC), ta suy ra O là tr ng tâm ọ
ABC∆
. G i ọI là trung đi m c a ể ủ BC, ta có:
3 3
2 2
a
AI BC= =
3 3
,
3 6
a a
OA OI⇒ = =
Trong m t ph ng (ặ ẳ ABC), ta v tia Oẽy vuông góc v i OớA. Đ t ặSO = h, ch n h tr c t a đ nh hình v ta đ c:ọ ệ ụ ọ ộ ư ẽ ượ
O(0; 0; 0), S(0; 0; h),
3; 0; 0
3
a
A
÷
3; 0; 0
6
a
I
⇒ −
÷
,
3; ; 0
6 2
a a
B
−
÷
,
3; ; 0
6 2
a a
C
− −
÷
,
3; ;
12 4 2
a a h
M
−
÷
và
3; ;
12 4 2
a a h
N
− −
÷
.
2
( )
5 3
, ; 0;
4 24
AMN
ah a
n AM AN
⇒ = = ÷
r uuuur uuur
,
2
( )
3
, ; 0; 6
SBC
a
n SB SC ah
= = −
÷
r uur uuur
2 2
2
( ) ( )
5 1 10
( ) ( ) . 0 ,
12 2 16
AMN SBC AMN
a a
AMN SBC n n h S AM AN
∆
⊥ ⇒ = ⇒ = ⇒ = =
r r uuuur uuur
.
2. Hình chóp t giácứ
a) Hình chóp S.ABCD có SA vuông góc v i đáy và đáy là hình vuông (ho c hìnhớ ặ
ch nh t). Ta ch n h tr c t a đ nh d ng tam di n vuông.ữ ậ ọ ệ ụ ọ ộ ư ạ ệ
b) Hình chóp S.ABCD có đáy là hình vuông (ho c hình thoi) tâm O đ ng cao ặ ườ SO vuông góc v i đáy. Taớ
ch n h tr c t a đ tia Oọ ệ ụ ọ ộ A, OB, OS l n l t là Oầ ượ x, Oy, Oz. Gi s ả ử SO = h, OA = a, OB = b ta có
O(0; 0; 0), A(a; 0; 0), B(0; b; 0), C(–a; 0; 0), D(0;–b; 0), S(0; 0; h).
c) Hình chóp S.ABCD có đáy hình ch nh t ữ ậ ABCD và AB = b.
SAD∆
đ u c nh a và vuông góc v i đáy. G iề ạ ớ ọ
H là trung đi m ểAD, trong (ABCD) ta v tia ẽHy vuông góc v i ớAD. Ch n h tr c t a đ ọ ệ ụ ọ ộ Hxyz ta có: H(0; 0; 0),
; 0; 0 , B ; b; 0
2 2
a a
A
÷ ÷
3
, ; b;0 , ; 0;0 , 0;0; .
2 2 2
a a a
C D S
− −
÷ ÷ ÷
3. Hình lăng tr đ ngụ ứ
Tùy theo hình d ng c a đáy ta ch n h tr c nh các d ng trên.ạ ủ ọ ệ ụ ư ạ
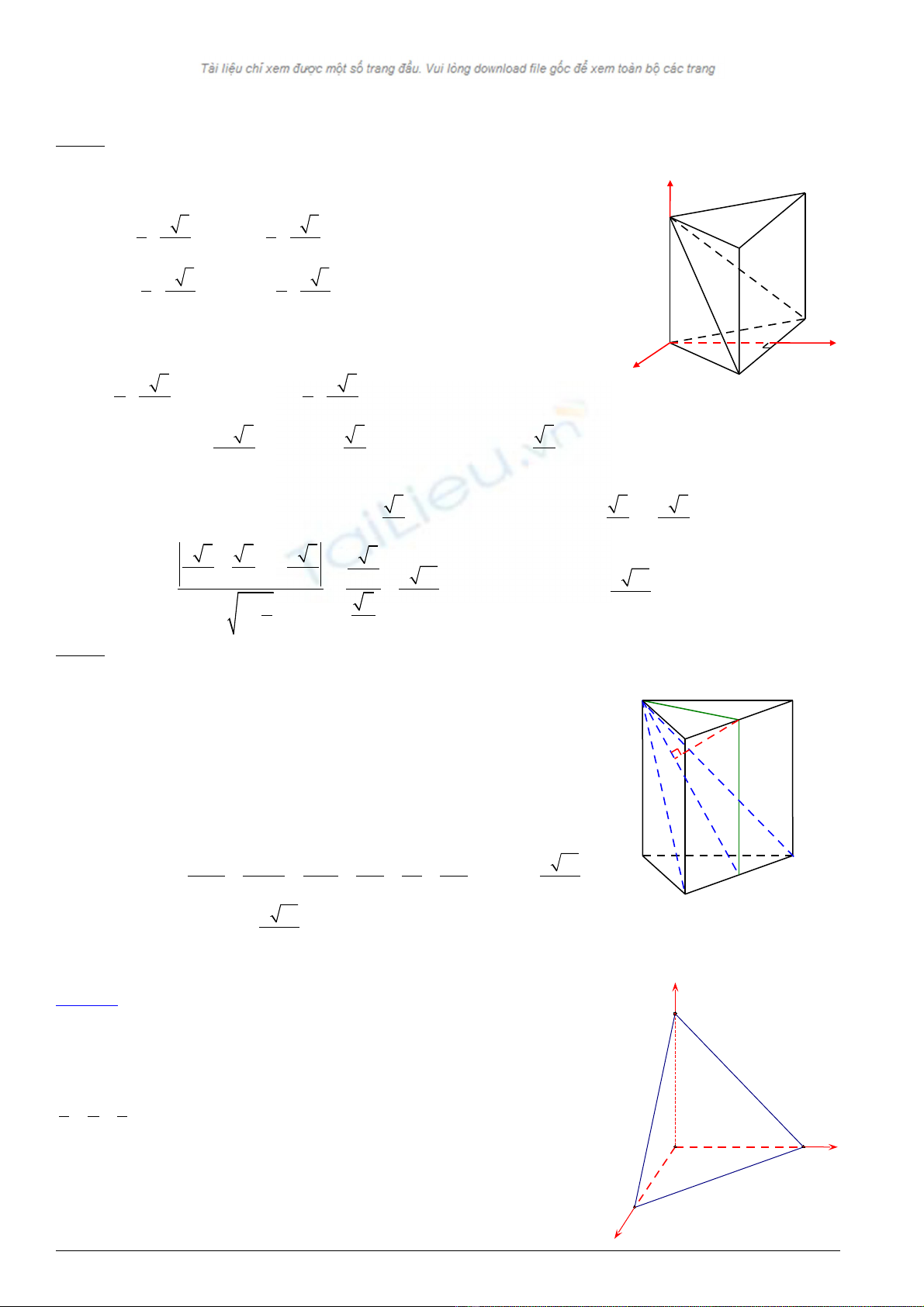
Ví d :ụ 1. Cho hình l p ph ng ậ ươ ABCD A'B'C'D' c nh ạa. Ch ng minh r ng ứ ằ AC'
vuông góc v i m t ph ng (ớ ặ ẳ A'BD).
L i gi iờ ả :
Ch n h tr c t a đọ ệ ụ ọ ộ Oxyz sao cho O ≡ A; B ∈ Ox; D ∈ Oy và A' ∈ Oz .
⇒ A(0;0;0), B(a;0;0), D(0;a;0), A'(0;0;a), C'(1;1;1)⇒ Ph ng trình đo nươ ạ
ch n c a m t ph ng(ắ ủ ặ ẳ A'BD): x + y + z = a hay x + y + z –a = 0
⇒Pháp tuy n cếa m t ph ng (ủ ặ ẳ A'BC):
( )
( )
'
1;1;1
A BC
n=
r
và
( )
' 1;1;1AC =
uuuur
.
V y ậAC' vuông góc v i (ớA'BC)
Chuyên đ : ềPH NG PHÁP T A Đ TRONG KHÔNG GIAN ƯƠ Ọ Ộ www.VNMATH.com
3
z
a
x
y
h
M
N
O
I
C
A
B
S
x
y
z
A
B
C
D
www.VNMATH.com
2. Cho lăng tr ụABC.A'B'C' các các m t bên đ u là hình vuông c nh ặ ề ạ a. G i ọD, F l n l t là trung đi m c a cácầ ượ ể ủ
c nh ạBC, C'B'. Tính kho ng cách gi a hai đ ng th ng ả ữ ườ ẳ A'B và B'C'.
Gi iả
Cách 1:
Vì các các m t bên c a lăng tr đ u là hình vuông nên ặ ủ ụ ề
' ' ' ' ' 'AB BC CA A B B C C A a= = = = = =
⇒ các tam giác ABC, A’B’C’ là các tam giác đ u.ề
Ch n h tr c ọ ệ ụ Axyz, v i ớAx, Ay, Az đôi m t vuông góc, ộA(0;0;0),
3 3
; ; 0 , ; ; 0 , '(0; 0; ),
2 2 2 2
3 3
' ; ; , ' ; ;
2 2 2 2
a a a a
B C A a
a a a a
B a C a
−
÷ ÷
−
÷ ÷
Ta có:
' ' // , ' ' // ( ' )B C BC B C A BC
( ) ( )
( )
( )
( )
' '; ' ' '; ' '; 'd B C A B d B C A BC d B A BC⇒ = =
3 3
' ; ; , ' ; ;
2 2 2 2
a a a a
A B a A C a
= − = − −
÷ ÷
uuuur uuuur
2
2 2 2
3 3
' ' 0; ; 0; 1; .
2 2
a
A B A C a a a n
∧ = = =
÷ ÷
uuuur uuuur r
, v i ớ
3
0; 1; 2
n
= ÷
r
Ph ng trình m t ph ng (ươ ặ ẳ A’BC) qua A’ v i vect pháp tuy n ớ ơ ế
n
r
:
3
0( 0) 1( 0) ( ) 0
2
x y z a− + − + − =
( )
3 3
' : 0
2 2
a
A BC y z⇔ + − =
( )
( )
3 3 3 3
.21
2 2 2 2
' ' .
7
3 7
14 2
a a a
aa
d B A BC
+ −
= = =
+
V y, ậ
( )
21
' ; ' ' .
7
a
d A B B C =
Cách 2:
Vì các các m t bên c a lăng tr đ u là hình vuông nên ặ ủ ụ ề
' ' ' ' ' 'AB BC CA A B B C C A a= = = = = =
⇒ các tam giác ABC, A’B’C’ là các tam giác đ u.ề
Ta có:
' ' // ' ' //( ' )B C BC B C A BC⇒
.
( ) ( )
( )
( )
( )
' ; ' ' ' '; ' ; 'd A B B C d B C A BC d F A BC⇒ = =
.
Ta có:
( ' )
' ( A'BC A')
BC FD BC A BC
BC A D
⊥
⇒ ⊥
⊥ ∆
caân taïi
D ng ự
'FH A D⊥
Vì
( ' ) ( ' )BC A BC BC FH H A BC⊥ ⇒ ⊥ ⇒ ⊥
∆A’FD vuông có:
2 2 2 2 2 2
1 1 1 4 1 7 21 .
7
' 3 3
a
FH
FH A F FD a a a
= + = + = ⇒ =
V y, ậ
( )
21
' ; ' ' 7
a
d A B B C FH= =
3. T di n ứ ệ ABCD có AB, AC, AD đôi m t vuông góc v i nhau, ộ ớ AB = 3, AC=AD=4. Tính kho ng cách tả ừ A t i m tớ ặ
ph ng (ẳBCD)
L i gi iờ ả
+ Ch n h tr c t a đ Oọ ệ ụ ọ ộ xyz sao cho A ≡ O.
D ∈Ox; C ∈ Oy và B ∈ Oz
⇒ A(0;0;0); B(0;0;3); C(0;4;0); D(4;0;0)
⇒ Ph ng trình m t ph ng (ươ ặ ẳ BCD) là:
1
4 4 3
yx z
+ + =
⇔ 3x + 3y + 4z - 12 = 0.
Suy ra kho ngr cách t ả ừ A t i m t ph ng (ớ ặ ẳ BCD).
II. Lyuy n t pệ ậ
Chuyên đ : ềPH NG PHÁP T A Đ TRONG KHÔNG GIAN ƯƠ Ọ Ộ www.VNMATH.com
4
A’
B’
C’
C
B
A
F
D
H
A’
C’
B’
A
B
C
D
x
a
z
y
www.VNMATH.com
B ài 1 : Cho hình chóp SABC có đ dài các c nh đ b ng 1, O là tr ng tâm c a tam giác ộ ạ ề ằ ọ ủ ∆ABC. I là trung đi m c aể ủ
SO. 1. M t ph ngặ ẳ (BIC) c t ắSA t i ạM. Tìm t l th tích c a t di n ỉ ệ ể ủ ứ ệ SBCM và t di nứ ệ SABC.
2. H là chân đ ng vuông góc h t ườ ạ ừ I xu ng c nh ố ạ SB. Ch ng minh r ng ứ ằ IH qua tr ng tâm ọG c a ủ∆SAC.
L i gi iờ ả
1. Ch n h tr c t a đ Oọ ệ ụ ọ ộ xyz sao cho O là g c t a đ . ố ọ ộ A∈Ox, S∈Oz, BC//Oy
⇒
3;0;0
3
A
÷
÷
;
3 1
; ;0
6 2
B
− −
÷
÷
;
3 1
; ;0
6 2
C
−
÷
÷
;
6
0;0 3
S
÷
÷
;
6
0;0; 6
I
÷
÷
Ta có:
(0;1;0)BC =
uuur
;
3 1 6
; ;
6 2 6
IC
= − −
÷
÷
uur
;
6 3
, ;0;
6 6
BC IC
⇒ = −
÷
÷
uuur uur
⇒ Ph ng trình m t ph ng (ươ ặ ẳ IBC) là:
6 3 6
( 0) 0( 0) ( ) 0
6 6 6
x y z− − + − + − =
Hay:
6
2 0
6
z− + − =
mà ta l i có: ạ
3 6
;0; // (1;0; 2)
3 3
SA
SA SA u
= − ⇒ −
÷
÷
uur uur r
.
Phưng trình đ ng th ng ơ ườ ẳ SA:
3; 0; 2
3
x t y z t= + = = −
.
+ T a đ đi m ọ ộ ể M là nghi m c a h : ệ ủ ệ
3(1)
3
0 (2)
2 (3)
6
2 0 (4)
6
x t
y
y t
x z
= +
=
= −
− + − =
.
Thay (1), (2), (3) và (4):
3 6 3 6
; 0; ;0;
12 4 12 4
x y z M
⇒ = = = ⇒ ÷
÷
;
3 6
;0; 4
12 12
SM SA SM
⇒ = − ⇒ =
÷
÷
uuur uur uuur
⇒ M n m trên đo n ằ ạ SA và
1
4
SM
SA =
( )
1
( ) 4
SBCM
SABC
V
V
⇒ =
.
2. Do G là tr ng tâm c a tam giác ọ ủ ∆ASC
⇒ SG đi qua trung đi m ểN c a ủAC
⇒ GI ⊂ (SNB) ⇒ GI và SB đ ng ph ng (1)ồ ẳ
Ta l i có ạ
3 1 6
; ;
18 6 9
G
÷
÷
3 1 6
; ;
18 6 18
GI
⇒ = − −
÷
÷
uur
3 1 6
; ;
18 6 18
GI
⇒ = − −
÷
÷
uur
. 0 (2)GI SB GI SB⇒ = ⇒ ⊥
uur uur
T (1) và (2) ừ
GI SB H⇒ ⊥ =
.
Bài 2: Cho hình chóp O.ABC có OA = a, OB = b, OC = c đôi m t vuông góc. Đi m ộ ể M c đ nh thu c tam giác ố ị ộ ABC
có kho ng cách l n l t đ n các m t ph ng (Oả ầ ượ ế ặ ẳ BC), (OCA), (OAB) là 1, 2, 3. Tính a, b, c đ th tích O.ể ể ABC nhỏ
nh t.ấ
H ng d n gi iướ ẫ ả
Ch n h tr c t a đ nh hình v , ta có:ọ ệ ụ ọ ộ ư ẽ
O(0; 0; 0), A(a; 0; 0), B(0; b; 0), C(0; 0; c).
d(M, (OAB)) = 3 ⇒ zM = 3.
T ng t ươ ự ⇒ M(1; 2; 3).
⇒ (ABC):
1
yx z
a b c
+ + =
1 2 3
( ) 1M ABC abc
∈ ⇒ + + =
(1).
.
1
6
O ABC
V abc=
(2).
Chuyên đ : ềPH NG PHÁP T A Đ TRONG KHÔNG GIAN ƯƠ Ọ Ộ www.VNMATH.com
5
z
x
y
I
O
H
A
C
S
G
N
M
z
x
y
I
O
B
A
C
S
x
c
z
b
y
a
x
3
H
O
C
B
A
M