Lecture "Applied data science: Linear regression (review)" includes content: the regression model formulation, understanding the regression results, potential problems in regression model,... We invite you to consult!
AMBIENT/
Chủ đề:
Nội dung Text: Lecture Applied data science: Linear regression (review)
- Linear regression (review)
- Overview
1. Introduction 8. Validation
2. Application 9. Regularisation
3. EDA 10. Clustering
4. Learning Process 11. Evaluation
5. Bias-Variance Tradeoff 12. Deployment
6. Regression (review) 13. Ethics
7. Classification
- Lecture outline
- The regression model formulation
- Understanding the regression results
- Potential problems in regression model (and its training data)
- The linear regression formulation
Approximated by
By minimising
- An example…
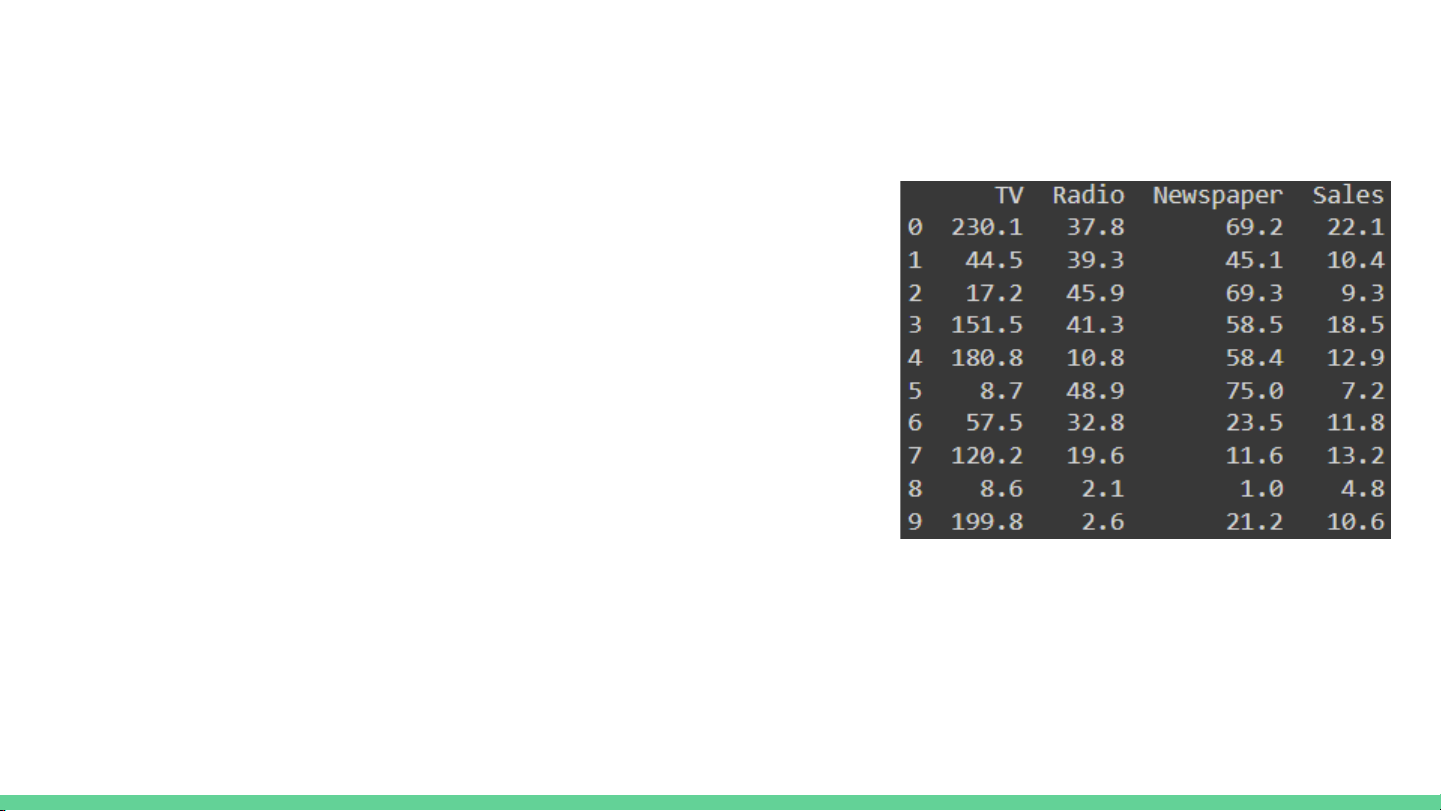
The ‘Advertising’ dataset
- Sales in 200 different markets together with
budget spent on marketing on 3 media types,
TV, Radio and Newspaper.
- Unit of Sales is in ‘thousand units’
- Unit of market budget is in ‘thousand dollars’
We have been given a regression model of Sales
on TV, Radio and Newspaper…
- Some of the results from the model
- Interpreting the regression results
Some of the questions we can (and should) ask
- Which media contribute to sales?
- How strong is the relationship?
- How accurate is the effect of each medium on sales?
- How accurately can we predict future sales?
- Is the relationship strictly linear?
- Which media contributes to sales?
Sample regression model vs population regression model
- Which media contributes to sales?
In other words, how confident are we that each beta is non-zero?
If t-statistic of each beta is very large (or its p-value is very
small), then we are confident that beta is non-zero.
But …
● What if we have a large beta but p-value is also large?
● What if we have a (very) small beta but p-value is small?
- How strong is the relationship?
R-squared: the proportion of variance in the response
explained by the model.
Residual standard error (RSE): the standard deviation
of the response from the population regression.
- How accurate is the effect of each medium on sales?
The 95% confidence interval of each
beta is (following the empirical rule)
Notes. Factor 2 is an approximate, can
be replaced by the 97.5% quantile of a
Student distribution with a degree of
freedom of n-2 (n is the number of data
points).
- How accurately can we predict future sales?
Potential sources of errors
- Model bias (the true relationship is not linear)
- Inaccuracy of the coefficient estimates => use confidence interval to determine
how close the estimated response is to the true response
- Random error, e.g. noise => use prediction interval to determine how close the
estimated response is to the observed response.
- How accurately can we predict future sales?
If we are to invest $100,000 into TV and $20,000 into Radio,
prediction outputs from the Sales ~ TV + Radio model is as below
(for 95% intervals).
● The predicted sales is 11256 units.
● The (actual) average sales across 200 markets will be
between [10985, 11528] units (with 95% confidence)
● The actual sales in a market will be between [7930, 14583]
units (with 95% confidence)
- Is the relationship strictly linear?
Residual plots usually reveal much information about the fitted model
- Is the relationship strictly linear?
Regression model Sales ~ TV + Radio + (TV x Radio)
- Other problems
Below are potential problems within the training data that would significantly
reduce the quality of fit of the OLS model and impacts our confidence in using the
model, either for predictions or for inferences.
- Outliers and high leverage points
- Collinearity
- Non-constant variance of error terms
- Outliers and high leverage points
Outliers - data points for which the response are far from the
value predicted by the fitted model.
High leverage points - data points which have unusual
predictors.
Outliers and high leverage points reduce the quality of fit of
OLS regression models and should be removed from the
training data before OLS fitting.
- Outliers and high leverage points
Regression results from fitting Sales ~ TV + Radio on
the new dataset…
- Collinearity (and multicollinearity)
Collinearity is when a predictor is correlated with another predictor => correlation matrix of
predictors would reveal this.
Multicollinearity is when a predictor is correlated with many other predictors => must be
detected variance inflation factor VIF of each predictor.
● Smallest possible value for VIF is 1 (no collinearity).
● VIF larger than 5 or 10 indicates worrying collinearity
(When) should we worry about (multi)collinearity?
- Non-constant variance of error terms
An important assumption in OLS regression is that epsilon has a constant variance. The
calculation of standard errors (thus confidence intervals and our conclusions on which
predictors affect the response) relies on this assumption.
Plot of residuals against fitted values
can reveal if such is the case.
Thêm vào BST
Báo xấu
Download
Vui lòng tải xuống để xem tài liệu đầy đủ
