Megabook Chuyên Gia Sách Luyện Thi Trang 1
MÔN TOÁN
Thời gian làm bài: 180 phút, không kể thời gian phát đề
Câu 1 (2,0 điểm). Cho hàm số
21
1
x
yx
(C).
a) Khảo sát sự biến thiên và vẽ đồ thị hàm số (C).
b) Tìm hệ số góc
k
của đường thẳng d đi qua điểm
1;2M
, sao cho
d
cắt
C
tại hai điểm phân biệt
,AB
. Gọi
,
AB
kk
là hệ số góc của các tiếp tuyến của đồ thị
C
tại
A
và
B
. Tìm các giá trị của
k
để
đạt
giá trị nhỏ nhất.
Câu 2 (1,0 điểm). Giải phương trình
1 sin 2sin2 6cos 2sin 3 2
2cos 1
x x x x
x
.
Câu 3 (1,0 điểm). Tính tích phân
2
1
0
21
ln 1
1
x
I x dx
x

.
Câu 4 (1,0 điểm).
a) Tìm tất cả các số phức
z
thỏa mãn
2 3 1z z i
và
12z i z i
là số thực.
b) Trong một hộp gồm có 8 viên bi xanh và 6 viên bi trắng, chọn ngẫu nhiên 5 viên bi. Tính xác suất để 5
viên bi được chọn có cả bi xanh và bi trắng.
Câu 5 (1,0 điểm). Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( ) : 2 2 7 0x y z
và đường
thẳng
1
22
:1 2 2
y
xz
d


. Viết phương trình mặt phẳng
chứa
d
và tạo với
một góc
sao cho
4
cos 9

.
Câu 6 (1,0 điểm). Cho hình chóp
.S ABC
có đáy là tam giác
ABC
vuông tại
A
,
,2AB a BC a
, góc giữa
hai mặt phẳng
SAC
và mặt phẳng đáy bằng
0
60
, tam giác
SAB
cân tại
S
thuộc mặt phẳng vuông góc với
mặt phẳng đáy. Tính thể tích khối cầu ngoại tiếp hình chóp
.S ABC
và khoảng cách giữa hai đường thẳng
AB
và
SC
.
Câu 7 (1,0 điểm). Trong mặt phẳng với hệ tọa độ
Oxy
, cho tam giác
ABC
nhọn nội tiếp đường tròn
C
có
phương trình
22
25xy
,
AC
đi qua
2;1K
, hai đường cao
BM
và
CN
. Tìm tọa độ các đỉnh
,,A B C
biết
A
có hoành độ âm và đường thẳng
MN
có phương trình
4 3 10 0xy
.
Câu 8 (1,0 điểm). Giải hệ phương trình
2
1
11
21
2 4 8
x
x
xx
.
Câu 9 (1,0 điểm). Cho
,xy
là các số thực dương thỏa mãn
2xy
. Tìm giá trị nhỏ nhất của biểu thức
2
334
27 10
98
y
x
Pyx

.
..................HẾT..................
ĐỀ TẶNG KÈM SỐ 2
Megabook Chuyên Gia Sách Luyện Thi Trang 2
HƯỚNG DẪN GIẢI
Câu 1.a.
- Tập xác định:
/1DR
.
- Sự biến thiên:
+ Chiều biến thiên:
2
1
'
1
y
x
.
' 0, ; 1 1;yx
, suy ra hàm số đồng biến trên các khoảng
;1
và
1; 
.
+ Cực trị: Hàm số không có cực trị.
+ Giới hạn:
lim 2; lim 2
xx
yy
 

đồ thị hàm số có tiệm cận ngang là
2y
.
11
lim ; lim
xx
yy

 

đồ thị hàm số có tiệm cận đứng là
1x
.
+ Bảng biến thiên
x

1

'y
y
2


2
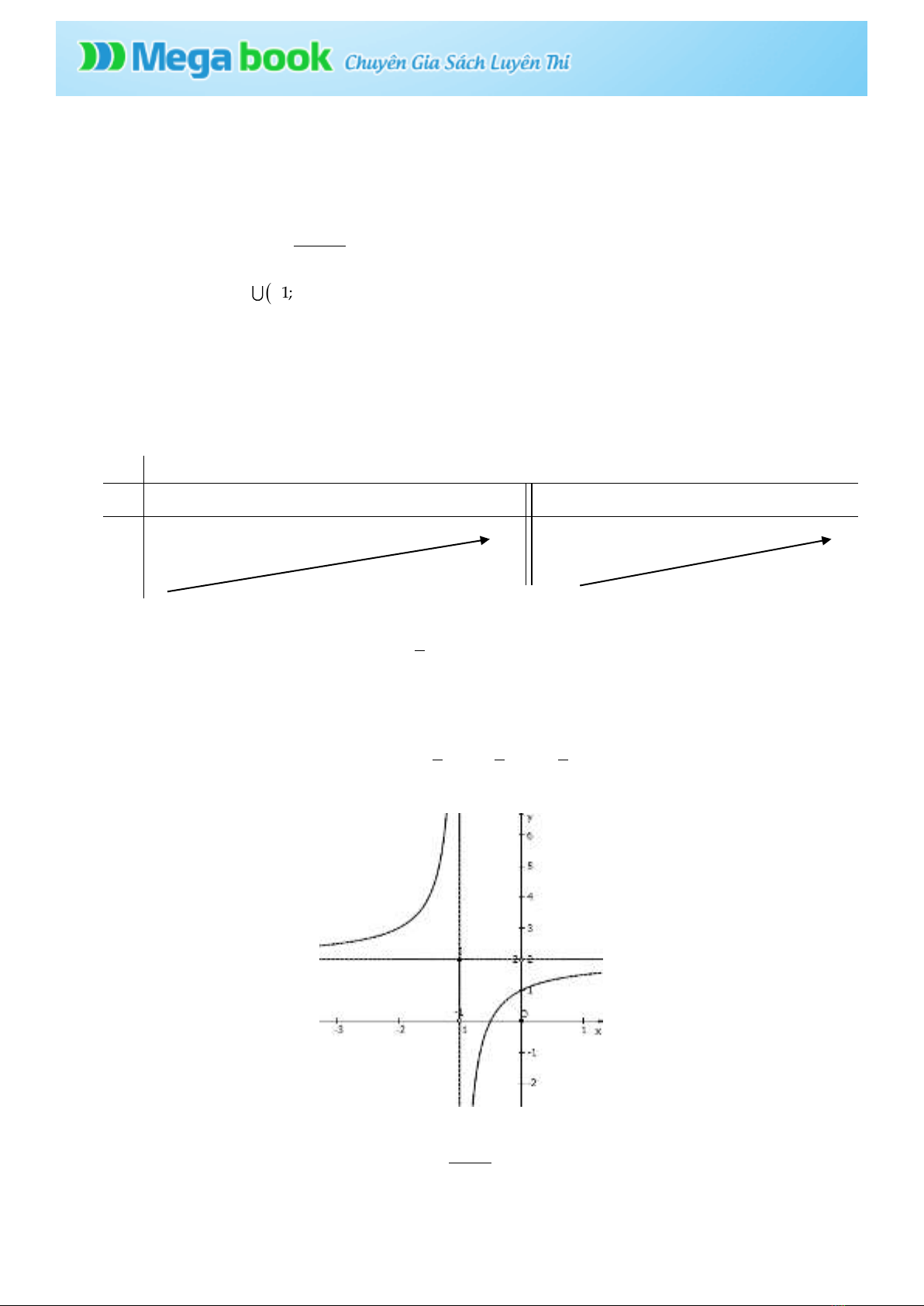
- Đồ thị:
+ Đồ thị hàm số cắt trục
Ox
tại điểm
1;0
2



.
+ Đồ thị hàm số cắt trục
Oy
tại điểm
0;1
.
+ Đồ thị hàm số giao điểm
1;2I
của hai tiệm cận làm tâm đối xứng.
+ Đồ thị hàm số đi qua các điểm
3 1 3
2; 3 , ; 4 , ;0 , 1;
2 2 2
.
- Vẽ đồ thị:
Câu 1.b. Phương trình đường thẳng
d
là
12y k x
.
Để
d
cắt
C
tại 2 điểm phân biệt khi phương trình
21 2
1
xkx k
x
có 2 nghiệm phân biệt
Tức phương trình
22 1 0kx kx k
có 2 nghiệm khác
1
.
Megabook Chuyên Gia Sách Luyện Thi Trang 3
2
0, 2 1 0 0
' 1 0
k k k k k
k k k
.
Ta có
2
1
'
1
y
x
. Suy ra
22
11
;
11
AB
AB
kk
xx


trong đó
,
AB
xx
là nghiệm của phương trình
22 1 0kx kx k
.
Nên
2
2
11 1
1
AB
BA
kx
kx
và
,
AB
xx
thỏa mãn
2
11kx
.
Suy ra
1 1 1
22
AB
k k k k k
k k k
, đẳng thức xảy ra khi
1k
.
Vậy
1
A
B
kk
đạt giá trị nhỏ nhất bằng 2 khi
1k
.
Nhận xét: Phương trình đường thẳng đi qua một điểm nào đó và cắt đồ thị hàm số cho trước tại
n
điểm thỏa
mãn tính chất của tiếp tuyến tại các hoàng độ giao điểm. Ta lập phương trình đường thẳng rồi tìm giao điểm
của nó với hàm số , sau đó biện luận các yêu cầu của bài toán.
Nhắc lại kiến thức và phương pháp:
-Phương trình đường thẳng đi qua điểm
,
QQ
Q x y
hệ số góc
k
có phương trình:
QQ
y k x x y
.
-Bất đẳng thức
AM GM
:
, 0 2a b a b ab
. Dấu bằng xảy ra
ab
.
Áp dụng cho bài toán:
- Phương trình đường thẳng đi qua M hệ số góc
k
là
12y k x
.
- Lập phương trình hoành độ giao điểm.
d
cắt
C
tại hai điểm phân biệt
2
, 2 1 0A B f x kx kx k
có hai nghiệm phân biệt
1x
.
- Hệ số góc tiếp tuyến tại
,AB
lần lượt là
,
AB
kk
(
,
AB
xx
là nghiệm của phương trình
0fx
). Khi đó tìm
được
1
A
B
kk
với
1
1 1 2
AB
k x k k k k
( theo
AM GM
).
Bài toán kết thúc.
Bài tập tương tự:
a. Cho hàm số
21
1
x
yx
. Lập phương trình tiếp tuyến của độ thị biết tiếp tuyến cắt các trục tọa độ
,Ox Oy
lần lượt tại A,B thỏa mãn
4
OA
OB
. Đáp số:
1 5 1 13
;
4 4 4 4
y x y x
.
b. Cho hàm số
2
2
x
yx
. Viết phương trìn tiếp tuyến của đồ thị biết tiếp tuyến tạo hai trục tọa độ một
tam giác có diện tích bằng
1
18
. Đáp số:
91
42
yx
.
Câu 2. Điều kiện
22;
3
x k k
.
Phương trình tương đương
1 sin 4sin cos 6cos 2sin 3 2
2cos 1
x x x x x
x
2
sin 1
1 sin 2sin 3 2cos 1 2 1 sin 2sin 3 2 2sin sin 1 0 1
2cos 1 sin 2
x
x x x x x x x
xx

Megabook Chuyên Gia Sách Luyện Thi Trang 4
2
2
2
6
52
5
xk
xk
xk
.
Phương trình có nghiệm:
5
2 ; 2 ; 2 ;
2 6 5
x k x k x k k
Z
.
Nhận xét: Phương pháp sử dụng phân tích nhân tử, giải phương trình cơ bản. Để giải phương trình ta sử
dụng công thức cơ bản nhân đôi, đặt nhân tử chung. Lưu ý kiểm tra điều kiện để kết hợp nghiệm.
Nhắc lại kiến thức và phương pháp:
-Sử dụng công thức góc nhân đôi
sin2 =2sin cos
.
-Nhóm nhân tử chung , thu được phương trình bậc 2 cơ bản.
-Giải phương trình bậc 2 ẩn duy nhất
sin x
tìm đươc
x
với công thức nghiệm:
+
2
sin ;
2
xk
x k Z
xk
.
+
cos cos 2 ;x x k k Z 
.
-Kiểm tra điều kiện ta thu được nghiệm của phương trình.
Bài tập tương tự:
a. Giải phương trình
sin2 cos2 cot tan
cos sin
xxxx
xx
. Đáp số:
2
3
xk
.
b. Giải phương trình
3
tan 3 cos sin .tan
2
x x x x



. Đáp số:
7
,2
6
x k x k
.
Câu 3.
11
00
ln 1
4 ln 1 1
x
I x x dx dx
x

.
1
0
4 ln 1A x x dx
.
Đặt
2
ln 1 1
1
2
dx
du
ux x
x
dv xdx v



.
1
1
22
1
0
00
1 1 1
4 ln 1 1 4 1
2 2 2 2
xx
A x x dx x











.
1
2
11 2
00
0
ln 1 ln 1 1
ln 1 ln 1 ln 2
1 2 2
xx
B dx x d x
x


.
Vậy
2
1
1 ln 2
2
I
.
Nhận xét: Đặc điểm biểu thức dưới dấu tích phân khó có thể đổi biến số và sử dụng tích phân từng phần. Ta
tách tích phân ban đầu thành 2 tích phân nhỏ.
Nhắc lại kiến thức và phương pháp:
-Công thức tính tích phân từng phần :
.'
b
b
a
a
I u v u vdu
.
-Công thức tính
1
1
b
bn
n
aa
x
x dx n
.
Megabook Chuyên Gia Sách Luyện Thi Trang 5
-Nhận thấy
2
2 1 4 1 1
11
x x x
xx

, nên ta có
I A B
.
- Tính
A
: Sử dụng công thức tính tích phân từng phần với
2
ln 1
1
2
ux
x
v

.
- Tính
B
:
1
0
ln 1
1
x
B dx
x
. Nhận thấy
1
ln 1 ' 1
xx

nên ngầm đặt ẩn phụ
ln 1tx
chuyển về công
thức
'. n
u u du
.
Bài tập tương tự:
a. Tính tích phân
1
0
2 ln
1 ln
x x x
I dx
xx

. Đáp số:
3 2ln2Ie
.
b. Tính tích phân
3
2
22
2 ln ln 3
1 ln
e
e
x x x x
I dx
xx

. Đáp số:
32
3ln2 4 2I e e
.
Câu 4.a. Giả sử số phức
z
có dạng:
;,z a bi a b
1 2 1 1 2 1 1 2z i z i a a b b a b a b i


1 1 2 0 1a b a b a b
2 2 2
2
2 3 1 2 3 4 1 1z z i a b a b
221
3 11 6 0 3, 2; ,
33
a a a b a b
.
Vậy
21
3 2 ; 33
z i z i
.
Nhận xét: Bài toán yêu cầu tìm số phức
z
thỏa mãn điều kiện nào đó. Ta chỉ cần đặt số phức có dạng chung
,z a bi a b R
rồi thay vào các điều kiện để giải ra
z
.
Nhắc lại kiến thức và phương pháp:
-Đặt
z a bi
,a b R
. Số phức
z
là số thực khi và chỉ khi phần ảo của nó bằng 0.
- Thay vào đẳng thức
2 3 1 1zz
. Sử dụng tính chất modul của số phức.
- Mặt khác ,
12z i z i
là số thực nên phần ảo bằng 0.
- Giải hệ cơ bản
2 2 2
2
2 3 4 1 1
1
a b a b
ab

tìm được
,ab
thu được số phức
z
cần tìm.
Bài toán kết thúc.
Bài tập tương tự:
a. Tìm số phức
z
thỏa mãn
21 11z i z i
. Đáp số:
3 2 , 2 3z i z i
.
b. Tìm số phức
z
thỏa mãn
1 2 3i z z i
. Đáp số:
11
44
zi
.
Câu 4.b. Số cách chọn ra 5 viên bi từ 14 viên bi là
5
14 2002C
(cách), suy ra, không gian mẫu là
2002
.
Gọi
A
là biến cố trong 5 viên bi được chọn có cả bi xanh và bi trắng.
Ta có
1 4 2 3 3 2 4 1
8 6 8 6 8 6 8 6 1940
AC C C C C C C C
.
Vậy
1940 970
2002 1001
A
PA
.